情境对大学生解决文字应用题的影响：来自眼动的证据

李晓东 付馨晨 鲁 成（.深圳大学 师范学院，广东 深圳 58060；.中山大学 南方学院，广东 广州 50970）

情境对大学生解决文字应用题的影响：来自眼动的证据

李晓东1*付馨晨1鲁 成2
（1.深圳大学 师范学院，广东 深圳 518060；2.中山大学 南方学院，广东 广州 510970）

考察情境是否影响大学生对文字应用题的信息加工。研究设计了两种情境：冲突与非冲突，文字应用题为一致和不一致比较问题。26名大学生参加了实验，结果表明，从解题成绩来看，情境对大学生解决文字应用题没有显著影响。但是从眼动指标来看，冲突情境增加了大学生的认知负荷，尤其在不一致冲突问题上表现更为明显。说明熟练解题者在解决问题时，仍需要构建情境模型。情境模型不是一种弱势模型，不会随着个体的认知成熟或专门知识的发展而消失。

情境模型；问题模型；比较问题；问题解决；眼动

一、引言

数学文字应用题是一类较为复杂的问题，它不仅要求学生能够阅读并理解文字材料所表达的数量关系，而且还要求学生能够将文字转化成数学表达并计算。在这种转化过程中，学生要建立两种心理表征：问题模型（problem model）和情境模型（situation model）。［1］

Kintsch和Greeno认为，学生一方面需要利用文本基点（text base）表征文本输入，另一方面需要建立一个抽象的问题表征，即问题模型。他们认为问题解决的关键是建构问题模型，它要求读者能够推断出文本基点中所没有的，但对解决问题而言所必须的信息，同时剔除文本基点中与解决问题无关的信息。问题模型包含三类用以表征和解决问题的知识结构的集合：（1）命题框架集合，用来将句子转化为命题；（2）表征集合的属性和关系的通用图式集合；（3）表征算术运算的通用图式集合。［2］Reusser认为，题目中的情境信息能促使情境模型建立，让个体根据自己的经验和现实世界的知识对题目进行解释。这些情境信息包括引发事件的原因（引发事件），事件的结果（解释），关于事件的时间结构（暂时），对主角和客体的有关描述（背景），等等，不同的情境信息将有助于对问题情境的分析，是理解文本与问题模型构建的中间阶段。［3］Coquin-Viennot和Moreau认为，情境模型表征的是语言和现实世界的知识，是用来帮助理解的；问题模型表征的是数理逻辑知识，是用来解决问题的。［4］Thevenot，Devidal，Barrouillet和Fayol认为，问题模型表征的是储存在长时记忆中的“刚性”（rigid）结构，代表的是文字应用题中各种成分，提取时是以表示语义关系的关键词或短语如“一共，多”等为基础的。情境模型是暂时的（不储存在长时记忆中）、流动的、建议性算法。［5］

一些研究者认为，情境模型有利于不成熟或低能力的个体解决问题，例如，对于“有5只小鸟，3只虫子，小鸟比虫子多几只？”这样的问题，只有25％的幼儿能正确回答；但是如果把上面的问题改为“小鸟比赛捉虫子，每只小鸟都能捉到虫子吗？有几只小鸟捉不到虫子？”则96％的幼儿都能正确回答。［6］Todal等人认为，学生在学习教科书中的问题时，可能会根据数字信息（如数字的相对大小决定谁减去谁）或对于不熟悉的题型会根据关键词线索启动计算。随着专门知识的发展，情境模型会被超越或自动化，学生在建构问题模型时不会受情境或明显矛盾的信息的影响。［1］

Coquin-Viennot和Moreau发现情境对小学生选择问题解决的策略有影响。她们给小学生呈现两种形式的问题。一种为：“花店要为14位获奖者每位准备5枝玫瑰和7枝郁金香，问花店一共要准备多少枝花？”另一种为：“花店要为14位获奖者每位准备一束有5枝玫瑰和7枝郁金香组成的花束，问花店一共要准备多少枝花？”结果发现第二种形式的问题，令小学生更多地使用因式分解策略即14×（5+7）而不是展开式策略即14×5+14×7。［7］

Coquin-Viennot和Moreau在另外一项研究中将问题分为两种，一种是情境模型与问题模型一致，如：“Jean站在体重计上称体重。Remi比Jean高，他比Jean重6公斤，Remi体重为58公斤，问Jean体重是多少？”一种是情境模型与问题模型不一致，如上面的问题改为Remi比Jean矮，其他不变。结果发现，小学生在不一致版本的问题上出现了更多的错误。说明问题图式并不是自动激活的，情境模型起到了中间表征的作用，当情境模型与问题模型不匹配时会损害问题解决。［4］

Mattarella-Micke和Beilock认为，情境模型并不必然误导读者并损害表现，相反数学问题表述的一个微小变化是以一种改变数字内容的可通达性的方式令情境模型发生改变、并对表现产生负面影响的。他们以大学生为被试，设计了两类题目，关联性题目是主人公的几个行为目的一致，如：“Brian路过一家商店时，进去买了7件衬衫。Brian买了3盒灯泡，每个盒子里有4个灯泡，问Brian一共买了几个灯泡？”分离性题目主人公的几个行为目的不一致，如上面题目中的第一句改为“Brian路过一家商店时，进去退了7件衬衫”。在高干扰条件下，被试需要在乘法和加法答案中进行选择，因为3+4=7，已经出现的加法答案会干扰被试正确选择乘法答案（3×4）；在低干扰条件下，题目第一句的数字则受到控制（如为6，则与加法答案7无关），因此加法答案对乘法答案的干扰就小。结果发现，被试在高干扰的关联性题目上错误更多，两个数字的和干扰了对它们乘积的提取，由于关联性题目与分离性题目只有一字之差（“买”和“退”），说明情境的微小变化也能损害表现。［8］

Thevenot采用再认范式对研究生解决简单比较应用题的心理表征进行了研究。首先要被试解决应用题，如“Louis有33个弹珠，Jean有17个弹珠。Louis比Jean多几个弹珠？”然后出其不意地要求其在4个问句中找出与原问句相同的句子。再认选项包括：（1）原问句；（2）与原问句关系一致，但人名顺序和语言表达均颠倒，如“Jean比Louis少几个弹珠？”；（3）人名顺序不变但语言表达颠倒，如“Louis比Jean少几个弹珠？”；（4）人名顺序颠倒但语言表达不变，如“Jean比Louis多几个弹珠？”。结果发现，第二句比第三句和第四句被更多地错误再认为原问句，第三句和第四句的再认成绩没有显著差异。第二句与原句在字面上差别是最大的，但是再认成绩却仅次于原句，说明被试表征的是情境中不同元素之间的一种关系，而不是如“比……多vs.比……少”这样的图式。被试在解决算术应用题时建构的是一种心理模型而非命题表征。［9］

国内学者邢强和单永明研究发现，在文本表述中增加情境性措辞，强调了时序性、因果性和目的性的信息，丰富了问题陈述，有助于构建情境模型，促进对问题的理解，对小学三、四、五年级学生数学应用题的表征成绩有普遍的促进性。并且指出增加有意义的文本长度并不会降低问题成绩，儿童在解决有情节的数学应用题时会构建情境模型，情境性措辞增强了所描述的情境和行为的时间和功能性结构，因此情境模型至少是和问题模型同等重要。［10］最近，Orrantia，Muñez，Vicente，Verschaffel和Rosales以大学生为被试，考察了故事情境中主人公的行为与目的是否一致对解决数学变化题的影响，结果发现当主人公的行为与目的不一致时，被试反应时明显增长，说明情境对问题解决产生了影响。［11］

综上所述，目前关于情境模型与问题模型在数学问题解决中的作用主要围绕两个关键问题展开：第一，情境模型究竟是促进还是妨碍数学问题解决；第二，情境模型是否是一种弱势模型，当个体认知成熟或能力发展水平较高时，将被问题模型所取代。回顾以往研究主要存在以下不足：一是研究中所用的数学问题类型不一致，结果难以比较；二是研究采用的指标主要是错误率和反应时，对于被试在阅读中的加工理解主要还是推测，缺少更精确的指标。本研究拟采用眼动技术，研究情境是否对熟练解题者（大学生）在解决比较问题（compare problem）时产生影响。之所以采用比较问题，主要是相对于变化问题和组合问题，比较问题是一类更难的文字应用题，它具有特殊的语义结构。［12］比较问题由已知条件、关系和问题三个要件组成，在已知条件中给出一个变量的值（小明有3个苹果），关系句是根据一个变量来定义另一个变量（小刚比小明多5个苹果），问题是求另一个变量的值（小刚有多少个苹果？）。根据文字表达和数量关系是否一致可将比较问题分为一致问题和不一致问题，在一致问题中未知数是关系句的主语（小刚比小明多5个苹果），变量关系的表达（比……多）与所需要的算术运算是一致的（用加法）；不一致问题中未知数是关系句的宾语（小明比小刚少5个苹果），变量关系的表达（比……少）与所需要的算术运算是不一致的（用加法）。［13］本研究提出如下假设：如果大学生在解决数学文字应用题时仍需要建构情境模型，则说明情境模型并不是一种弱势模型；情境对问题解决的影响受情境模型与问题模型的关系影响，如果二者关系是一致的，情境会促进问题解决；如果二者关系是冲突的，则情境将损害问题解决。

二、实验方法

（一）被试

被试为在校大学生共34人，其中男生16人，女生18人，平均年龄20.8岁。被试视力或矫正视力正常，无色盲，从未参加过此类型实验。

（二）实验材料

实验材料由自编的16道数学应用题组成，其中8道为比较问题，8道变化题或组合题作为过滤题，用来防止被试产生思维定势或倦怠。比较问题可以按情境模型与问题模型的关系分为冲突型情境问题/非冲突型情境问题（例如，某工厂甲乙两小组都生产喜羊羊玩具，甲组每天生产95个，乙组在引进先进技术设备后/乙组的技术设备比较落后，每天比甲组少生产59个玩具，乙组每天生产多少个玩具？）；又根据关系词是否与操作运算一致，将比较问题分为一致/不一致题目（某工厂甲乙两小组都生产喜羊羊玩具，甲组每天生产95个，乙组每天比甲组少生产59个玩具/甲组每天比乙组多生产59个玩具，乙组每天生产多少个玩具？）。七名心理学专业研究生对所有题目进行检验性阅读，确定题意表述清楚，题目适合于口头报告。实验过程中，记录被试的口语报告和眼动指标，对数据结果进行分析讨论。

（三）实验设计

采用2（情境类型：冲突，非冲突）×2（问题类型：一致，不一致）重复测量设计。自变量为情境类型与问题类型，均为组内变量，因变量为解题成绩及各项眼动指标。

（四）实验仪器

本实验使用美国应用科学实验室（Applied Science Laboratory，ASL）生产的504型眼动仪。该仪器的最高刷新频率为360Hz（即每秒记录眼动数据360次），考虑到该仪器使用的稳定性，将该仪器的刷新频率调至120Hz，可以对被试阅读及解决数学问题时的眼睛运动情况进行记录。另外，利用录音笔对被试的口头报告进行录音，判断被试是否正确回答问题。

（五）实验程序

主试负责操作眼动仪，电脑屏幕上呈现指导语，指导语为：“亲爱的同学，你好！欢迎你参加本次实验，在电脑屏幕上，将会出现一道数学问题，请你仔细阅读题目，又快又准地说出解题算式，不要求计算结果，口头报告完之后，迅速按‘J’键，稍作休息后，开始下一道题目。明白上述指导语后，请按‘J’键开始。”正式实验前要求被试进行出声思维的练习，并熟悉实验程序，直至被试完全明白指导语和实验程序后，才开始正式实验，要求被试在实验过程中尽可能保持头部不动。

采用E-prime编程技术，电脑屏幕上随机呈现数学问题，利用录音笔记录被试的口语报告结果，眼动仪记录被试阅读时的各项眼动指标。

（六）眼动记录指标

眼动仪记录以下指标：（1）总注视时间：将眼睛对准某个对象的活动叫作注视，一次注视也称为一个注视点。总注视时间是指解题结束时所有注视点所用时间的总和。（2）情境句注视时间：情境句定义为对理解题意有促进或阻碍作用的句子（如：乙组在引进先进技术设备后）。情境句注视时间是指注视情境句所有注视点所用时间的总和。（3）关系句注视时间：关系句定义为应用题中描述对象之间关系的句子（如：乙组每天比甲组少生产59个玩具）。关系句注视时间是指注视关系句所有注视点所用时间的总和。（4）注视次数：被试注视某个区域时注视点的个数，本研究记录总注视次数、情境句注视次数、关系句注视次数。（5）回视次数：本研究记录兴趣区间的回视，情境句回视次数和关系句回视次数。（6）瞳孔直径：刺激呈现期间瞳孔直径的平均值与刺激呈现前瞳孔直径的基线值之间的变化量。

三、实验结果

实验过程中由于8名被试因眼睛疲劳、斜视、散光等原因，眼动数据不符合要求，将其数据剔除，剩余有效被试26名，其中男生10人，女生16人，平均年龄20.5岁。对整理过的数据进行统计，26名被试在得分和各项眼动指标的数据结果见表1。

表1 冲突与非冲突两种情境条件下被试的得分及眼动指标

（一）冲突与非冲突情境下被试解决比较问题的成绩以及瞳孔直径的比较

被试答对1题计1分，答错计0分，非冲突一致性题目出现了天花板效应，而冲突不一致题目得分最低，对被试平均得分进行重复测量方差分析，结果表明，情境类型主效应不显著；问题类型的主效应显著，F（1，25）=11.63，p＜0.001，η2=0.32，不一致性题目的得分显著低于一致性题目；情境类型与问题类型的交互作用不显著，p＞0.05。

对瞳孔直径进行二因素重复测量方差分析，问题类型的主效应不显著；情境类型主效应显著，F（1，25）=9.74，p＜0.01，η2=0.28，冲突情境下的比较问题的瞳孔直径显著大于非冲突情境下；两因素之间交互作用不显著，p＞0.05。

（二）冲突与非冲突情境下被试对问题的总注视时间及总注视次数的比较

对总注视时间进行重复测量方差分析，情境类型的主效应显著，F（1，25）=61.53，p＜0.001，η2=0.71；问题类型的主效应也显著，F（1，25）=20.09，p＜0.001，η2=0.45；情境类型与问题类型的交互作用也达到显著性水平，F（1，25）=13.47，p＜0.001，η2=0.37，交互作用见图1，从中可以看出冲突情境下，对一致和不一致比较问题的总注视时间都比非冲突情境下的长，并且，在冲突情境下对不一致比较问题的总注视时间最长。

对总注视次数进行重复测量方差分析，情境类型的主效应显著，F（1，25）=78.08，p＜0.001，η2=0.76，问题类型的主效应也显著，F（1，25）=19.24，p＜0.001，η2=0.44；情境类型与问题类型的交互作用也达到显著性水平，F（1，25）=13.90，p＜0.001，η2=0.36，交互作用见图2，从中可以看出冲突情境下，对一致和不一致比较问题的总注视次数都比非冲突情境下的多，并且，在冲突情境下对不一致比较问题的总注视次数最多。

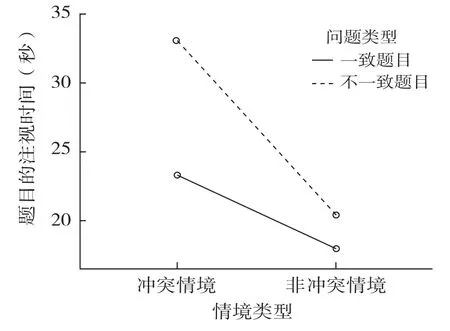
图1 冲突与非冲突情境类型下被试对题目的注视时间

图2 冲突与非冲突情境类型下被试对题目的注视次数

（三）冲突与非冲突情境下被试对情境句与关系句注视时间和注视次数的比较

对情境句注视时间进行重复测量方差分析，情境类型主效应显著，F（1，25）=58.67，p＜0.001，η2=0.70；问题类型的主效应也显著，F（1，25）=8.94，p＜0.001，η2=0.26；情境类型与问题类型的交互作用也达到显著性水平，F（1，25）=4.51，p＜0.05，η2=0.15，交互作用见图3，从中可以看出冲突情境下，对一致和不一致比较问题情境句的注视时间都比非冲突情境下的长，并且，在冲突情境下对不一致比较问题情境句的注视时间最长。

对情境句注视次数进行重复测量方差分析，情境类型主效应显著，F（1，25）=66.54，p＜0.001，η2=0.73；问题类型的主效应也显著，F（1，25）=8.60，p＜0.01，η2=0.26；情境类型与问题类型的交互作用也达到显著性水平，F（1，25）=4.28，p＜0.05，η2=0.15，交互作用见图4，从中可以看出冲突情境下，对一致和不一致比较问题情境句的注视次数都比非冲突情境下的多，并且，在冲突情境下对不一致比较问题情境句的注视次数最多。

图3 冲突与非冲突情境类型下被试对情境句的注视时间

图4 冲突与非冲突情境类型下被试对情境句的注视次数

对关系句注视时间进行重复测量方差分析，情境类型主效应显著，F（1，25）=49.64，p＜0.001，η2=0.67；问题类型的主效应显著，F（1，25）=13.01，p＜0.001，η2=0.34；情境与问题类型的交互作用也达到显著性水平，F（1，25）=4.97 p＜0.05，η2=0.17，交互作用见图5，从中可以看出冲突情境下，对一致和不一致比较问题关系句的注视时间都比非冲突情境下的长，并且，在冲突情境下对不一致题目关系句的注视时间最长。

对关系句的注视次数进行重复测量方差分析，情境类型主效应显著，F（1，25）=54.81，p＜0.001，η2=0.69；问题类型的主效应显著，F（1，25）=14.58，p＜0.01，η2=0.37；情境类型与问题类型的交互作用也达到显著性水平，F（1，25）=6.34，p＜0.05，η2=0.20，交互作用见图6，从中可以看出冲突情境下，对一致和不一致比较问题关系句的注视次数都比非冲突情境下的多，并且，在冲突情境下对不一致题目关系句的注视次数最多。

图5 冲突与非冲突情境类型下被试对关系句的注视时间

图6 冲突与非冲突情境类型下被试对关系句的注视次数

（四）冲突与非冲突情境下被试对情境句与关系句回视次数的比较

对情境句回视次数进行重复测量方差分析，情境类型主效应显著，F（1，25）=71.96，p＜0.001，η2=0.74；问题类型的主效应也显著，F（1，25）=18.53，p＜0.001，η2=0.43；情境类型与问题类型的交互作用也达到显著性水平，F（1，25）=5.55，p＜0.05，η2=0.16，交互作用见图7，从中可以看出冲突情境下，对一致和不一致比较问题情境句的回视次数都比非冲突情境下的多，并且，在冲突情境下对不一致题目情境句的回视次数最多。

图7 冲突与非冲突情境类型下被试对情境句的回视次数

图8 冲突与非冲突情境类型下被试对关系句的回视次数

对关系句的回视次数进行重复测量方差分析，情境类型主效应显著，F（1，25）=36.56，p＜0.001，η2=0.59；问题类型的主效应显著，F（1，25）=12.19，p＜0.01，η2=0.33；情境类型与问题类型的交互作用也达到显著性水平，F（1，25）=4.87，p＜0.05，η2=0.16，交互作用见图8，从中可以看出冲突情境下，对一致和不一致比较问题关系句的回视次数都比非冲突情境下的多，并且，在冲突情境下对不一致题目关系句的回视次数最多。

四、讨论

本研究发现，大学生在解决一致性比较问题上的成绩明显好于不一致问题，出现了一致性效应。尽管不一致问题仅涉及简单的算术运算，大学生仍出现了较多的错误，这种错误不是计算错误，而是对于变量关系的错误表征，说明不一致问题比一致问题更难。这一结果与国内外的研究是一致的。［12-16］

从解题成绩来看，情境对问题解决并无影响，既没有促进也没有损害被试的表现，与以往的研究不一致。［8-9，11］这可能是由于本研究与其他研究采用的问题不一致或研究范式不同造成的，也可能是情境信息主要功能在于促进或阻碍解题者对题意的理解，构建与数学逻辑关系表征相对应的情境表征，当情境信息与隐含的逻辑信息出现形式上的冲突，被试可能会故意抑制或忽略情境信息，来获得所要的解题答案。［18］但从眼动指标来看，情境对个体的信息加工是有影响的。以往研究表明，信息加工负荷量大小与任务难度影响瞳孔直径的变化，瞳孔直径越大，心理负荷越大。［19-20］本研究发现，在冲突情境下，被试解题时的瞳孔直径要比非冲突情境下的瞳孔直径更大。被试在冲突情境下比非冲突情境需要更多的心理资源，心理负荷加大，说明被试在解决数学文字应用题时，并没有忽略情境信息，相反情境信息的冲突对解题带来了很大的干扰，进一步充分说明，被试解决数学应用题时不仅构建问题模型，而且构建情境模型，当两种模型存在冲突，则给解题者带来很大的困扰，这一结果与以往研究一致。［4］

对被试解决比较问题时眼动的注视时间和次数进行分析，发现被试的总注视时间和次数、情境句和关系句的注视时间、注视次数、回视次数等眼动指标有明显的规律性，无论是在一致比较问题还是在不一致比较问题上，被试在冲突情境下，总注视时间和次数、对情境句和关系句的注视时间、注视次数及回视次数要显著多于非冲突情境。这说明被试在解决数学比较问题过程中，不仅会提取题目中必要的逻辑信息如数字、关系词，构建问题模型，而且还会对一些非逻辑信息如情境信息进行加工，构建相应的情境模型。由于大学生在解决数学文字应用题时仍需要建构情境模型，说明情境模型并不是一种弱势模型，不会随着个体的认知成熟或专门知识的发展而消失。当表征数学逻辑的问题模型与表征情境信息的情境模型相冲突时，即使被试为受过较好数学训练的大学生，在冲突情境下依然也会在理解题意上出现困难，需要更长的注视时间、更多的注视次数和回视次数，用来帮助他们确认逻辑信息。Nathan等人指出，即使是专家，在复杂的问题中（精心设计的场景或额外信息），由于没有遇到过这种情况，他们也会依赖于接近“真实生活”的情境模型。［21］

冲突情境下，被试在不一致比较问题上的总注视时间及次数，对情境句、关系句的注视时间、注视次数及回视次数都要显著多于一致比较问题，实验中的被试以前很少接触冲突情境下的比较问题，缺乏相应的解题图式，当他们意识到情境模型与数学逻辑模型发生冲突时，会消耗部分的工作记忆资源来化解这种冲突，同时由于不一致题目自身结构的特殊性，要比一致题目更为复杂，被试要用另一部分资源对不一致结构进行转换，这就导致了他们在冲突情境下，对不一致比较问题所需要的时间会更多一些，并且有时候这种转换不一定能成功，因此得分最低。［12，15-17，22］

在非冲突情境下，一致与不一致题目虽然在总注视次数，对情境句和关系句的注视时间与注视次数上没有显著性差异，但是在总注视时间以及对情境句、关系句的回视次数上，不一致问题要显著多于一致性问题。总注视时间的差异说明不一致问题的难度高于一致问题，Lubin等人运用反应时的研究也得到了类似的结果，而且指出在不一致条件下个体必须要克服内部所固有的一致性图式（“多”对应“加法”）才能正确回答比较问题，因此反应时增加。［23］回视次数多说明解题者在这个区域发现了问题，阻碍解题，所以多次回视确认，表明被试在解答不一致问题时，能意识不一致问题的难点在情境句和关系句的表达上。另外，本研究中情境信息插入的位置正是已知条件与关系句的中间，有可能干扰解题者理解问题中对象之间的关系，在语意不够流畅的情况下，解题者也会有更多的回视次数。［24］

五、结论及其对教育的启示意义

通过眼动数据的采集，本研究发现对于大学生这样的熟练解题者，在解决比较问题时，仍需要构建情境模型，当情境模型与问题模型不一致时，会增加被试的认知负荷，说明情境模型并不是一种弱势模型，情境模型并不会随着个体的认知成熟或专门知识的发展而消失。

强调重视问题解决过程中的情境模型的构建，实际上是强调重视学生对问题的理解。从20世纪80年代开始，国际数学教育界开始反思数学教育中存在的问题，其中一个就是教科书的问题模式化。其特征是：“结构良好，具有一个教师已知的答案；计算结果匀称完美；计算方法与解题相关的信息都在文字中，没有无关信息；问题明确，所有的问题都有解。”［3］这就导致学生在学习数学问题时容易形成定势，结果在解题时出现答案在数学上是正确无误的，在生活中却是说不通的情况。例如，对于“一辆军用车可容纳30个士兵，如果1 128个士兵将坐这种车去军事基地，需要租用多少辆军用车？”这样的问题，约有73％的13岁儿童得出的结果是37.6辆，或是37辆车，还余18，似乎他们认为车辆是可以分割的。说明学生在解数学题时，并没有联系生活实际情况。［18］

虽然数学教育的目的是让学生理解变量之间的数理逻辑关系，并学会用数学的方式表达这种关系。但是这种逻辑关系不应该脱离情境而存在，情境本身也是逻辑的一部分。学校教育的目标应该是通过有效的教学赋予学生一种一般性能力或迁移的能力，当学生离开正规的学校教育机构后，能够运用这种能力解决现实生活中的问题。然而，目前教科书问题缺乏鲜活的生活情境，学生在常年累月的练习中形成了对数学问题的刻板印象，使得他们对情境缺少敏感性，这会造成两个问题。第一是令学生在重视能力考察的学业水平测试中处于不利地位。国际数学教育质量评估的趋势是越来越重视学生的理解能力、监控能力以及在理解的基础上构建模型解决问题，这会导致学业水平评估的内容和形式发生改变，并最终影响数学教学。第二，无法学以致用。中国的学生在中小学阶段学习的数学知识在世界范围内来看都是很艰深的，但是很多人都会觉得生活中只要会加减乘除就可以了，中小学甚至大学的高等数学似乎只是培养学生形式逻辑的思维体操，没有实用价值。类比是迁移的基础，个体如果无法意识到生活中的问题与学校所学的问题有相似之处，就不会运用学校学习的知识去解决新问题。因而当面临生活和工作中的问题时就会束手无策，并对所受教育产生无意义或无价值的感受。

在数学教学中强调建立情境模型的意义在于，第一，可以鼓励学生用不同的策略、不同的路径去解决问题。题目中的情境信息会激活学生的生活经验，使得一些还不具备数理逻辑知识的儿童或者无法建构问题模型的儿童也可以解决问题，一方面提高了他们的学业成绩，另一方面也有利于他们建立较高的学业自我概念，提升自我效能，从而乐于学习数学。第二，可以促进学生元认知能力的发展，元认知是关于认知的认知，是个体对自己的思维过程进行监控、评价和调节的能力。情境会帮助个体去评估自己的答案是否在数学上和生活经验中都行得通、有意义，当个体发现答案在生活中讲不通时，他们就必须重新对问题进行审视和思考，调整解决问题的方案。

中国的基础数学教育虽然近年来也提倡生活数学的理念，但在实际践行中还没有得到充分的重视与落实，教师和教材编写者应该为此做出更多的努力，进一步探讨怎样将日常生活经验与学生数学问题解决的训练结合起来，切实帮助学生提高解决实际问题的能力，激发其数学学习兴趣与动机。

［1］Tolar T D，Fuchs L，Cirino P T，et al.Predicting Development of Mathematical Word Problem Solving Across the Intermediate Grades［J］.Journal of Educational Psychology，2012，104（4）.

［2］Kintsch W，Greeno J G.Understandingand Solving Word Arithmetic Problems［J］.Psychological Review，1985，92（1）.

［3］Reusser K.From Text to Situation to Equation：Cognitive Simulation of Understanding and Solving Mathematical Word Problems［J］.Instructional Science，1989，2（2）.

［4］Coquin-Viennot D，Moreau S.Arithmetic Problems at School：When There is an Apparent Contradiction Between the Situation Model and the Problem Model［J］.British Journal of Educational Psychology，2007，77（1）.

［5］Thevenot C，Devidal M，Barrouillet P，et al.Why Does Placing the Question Before an Arithmetic Word Problem Improve Performance？A Situation Model Account［J］.The Quarterly Journal of Experimental Psychology，2007，60（1）.

［6］Hudson T.Correspondences and Numerical Differences between Disjoint Sets［J］.Child Development，1983，54（1）.

［7］Coquin-Viennot D，Moreau S.Highlighting the Role of the Episodic Situation Model in the Solving of Arithmetical Problems［J］.European Journal of Psychology of Education，2003，18（3）.

［8］Mattarella-Micke A，Beilock S L.Situating Math Word Problems：The Story Matters［J］.Psychonomic Bulletin and Review，2010，17（1）.

［9］Thevenot C.Arithmetic Word Problem Solving：Evidence for the Construction of a Mental Model［J］.Actapsychologica，2010，133（1）.

［10］邢强，单永明.文本表述和结构对小学生数学应用题表征的影响［J］.心理发展与教育，2013，（3）.

［11］Orrantia J，Munez D，Vicente S，et al.Processing of Situational Information in Story Problem Texts.An Analysis from On-Line Measures［J］.The Spanish Journal of Psychology，2014，17.

［12］Lewis B，Mayer E.Student’s Miscomprehension of Relational Statements in Arithmetic Word Problems［J］.Journal of Educational Psychology，1987，79（4）.

［13］李晓东，张向葵，沃建中.小学三年级数学学优生与学困生解决比较问题的差异［J］.心理学报，2002，34（4）.

［14］Hegarty M，Mayer E，Monk A.Comprehension of Arithmetic Word Problems：A Comparison of Successful and Unsuccessful Problem Solvers［J］.Journal of Educational Psychology，1995，87（1）.

［15］李晓东，林崇德.小学3-6年级学生解决比较问题的研究［J］.心理科学，2002，25（3）.

［16］张锦坤，沈德立，藏传丽.算术应用题表征策略的眼动研究［J］.心理与行为研究，2006，4（3）.

［17］Hegarty M，Mayer R E，Green C E.Comprehension of Arithmetic Word Problems：Evidence from Students' Eye Fixations［J］.Journal of Educational Psychology，1992，84（1）.

［18］Inoue N.The Realistic Reasons Behind Unrealistic Solutions：The Role of Interpretive Activity in Word Problem Solving［J］.Learning and Instruction，2005，15（1）.

［19］张仙峰，叶文玲.当前阅读研究中眼动指标述评［J］.心理与行为研究，2006，4（3）.

［20］闫国利，熊建萍，臧传丽，等.阅读研究中的主要眼动指标评述［J］.心理科学进展，2013，21（4）.

［21］Nathan M J，Kintsch W，Young E.A Theory of Algebra-word-problem Comprehension and its Implications for the Design of Learning Environments［J］.Cognition and Instruction，1992，9（4）.

［22］Mayer R E，Hegarty M.The Process of Understanding Mathematical Problems［G］//Sternberg R J，Ben-Zeev T.The Nature of Mathematical thinking.Hillsdale，NJ：Lawrence Erlbaum Associates，1996.

［23］Lubin A，Vidal J，Lanoë C，et al.Inhibitory Control is Needed for the Resolution of Arithmetic Word Problems：A Developmental Negative Priming Study［J］.Journal of Educational Psychology，2013，105（3）.

［24］Van der Schoot M，Bakker Arkema A H，Horsley T M，et al.The Consistency Effect Depends on Markedness in Less Successful but not Successful Problem Solvers：An Eye Movement Study in Primary School Children［J］.Contemporary educational psychology，2009，34（1）.

［责任编辑：江 波］

The Effect of Situation on College Students’ Word Problem Solving：Evidence from Eye Movement

Li Xiao-dong1Fu Xin-chen1Lu Cheng2
（1.Normal College，Shenzhen University，Shenzhen Guangdong 518060，China；2.Nanfang College，Sun Yat-sen University，Guangzhou Guangdong 510970，China）

This study explored whether situations would influence processing of word problem solving.Two kinds of situations，namely，contradictory ones and consistent ones，were designed.26 college students participated in the experiment.The results showed that situations had no impact on the students’ performance；however，contradictory situations increased the cognitive load of college students according to the eye movement indicators，especially on inconsistent comparison problems.Experienced problem solvers still need to construct situation models.The situation model was not a weak model and would not disappear with the individual’s cognitive maturity or expertise development.

situation model；problem model；comparison problem；problem solving；eye movement

李晓东（1965— ），女，辽宁沈阳人，博士，深圳大学师范学院心理学系教授、博士生导师，主要从事发展与教育心理学研究。

B842.3

A

2095-7068（2015）01-0096-09

2014-12-25

*通讯作者：李晓东，E-mail：lxd_psy@163.com。