一种单信道时频重叠信号调制识别方法*

曾创展，贾 鑫，刘淑茜

(1.装备学院 研究生管理大队，北京 101416;2.装备学院 光电装备系，北京 101416;3.空天宽带网络技术协同创新实验室，北京 100094)

1 引言

通信信号调制识别就是通过对接收信号进行一系列信号处理后获取信号的调制方式的过程，是认知无线电技术的重要组成部分，被广泛应用于无线电监测和频谱管理。以往的调制识别方法主要是基于信号在时域或频域的区分性［1］来进行识别分类的，因而无法处理时频域上均重叠的信号。随着无线电应用的发展以及频谱资源短缺的现实约束，在同一信道中有意或无意出现时频重叠信号的情况愈加常见，因此，研究单信道时频重叠信号的调制识别方法也愈加重要。

应用盲源分离［2］的方法来将时频重叠信号转换为单信号是较常用的方法，如文献［3］采用独立分量分析的方法将独立信号分离开，然后提取信号的瞬时特征参数进行识别;文献［4］提出基于经验模态分解和分形盒维数的方法等。然而，信号进行盲源分离处理本身就需要多种先验知识，算法的适用范围也有局限，分离效果难以保证。因而研究人员提出了另一种识别时频重叠信号调制方式的方法，即直接特征提取法，如小波变换法［5］、循环平稳特征法［6］等。循环平稳特征法主要基于信号循环频率不同时受重叠信号影响这一特性，主要研究有:文献［7］提出基于循环谱包络的识别方法，能在较少先验知识和较低的信噪比条件下获得较好的识别效果，但其识别类型为M 进制相移键控(M－Phase Shift Key，MPSK)信号和最小频移键控(Minimum Shift Key，MSK)信号;文献［8］提出基于四阶循环累积量特征的方法，通过对信号进行预处理，由载频和码速率估计基带信号的循环频率，计算信号的高阶循环累积量特征，从而进行调制类型的识别，其能有效识别时频重叠MPSK 信号，但在低信噪比下识别效果一般。

为克服上述方法识别类型少和低信噪比下效果差的不足，本文通过提取信号延迟相关和瞬时自相关特征，对15 种单信道时频重叠双信号组合(信号集为{2ASK;BPSK;QPSK;2FSK;4FSK})进行识别分类，实现了低信噪比下的单信道时频重叠双信号的调制识别。

2 信号相关特性

信号相关特性主要是根据理想高斯白噪声在延迟非零处相关为零的特点，包括延迟相关函数和瞬时自相关函数。

定义1 信号延迟相关函数。记为

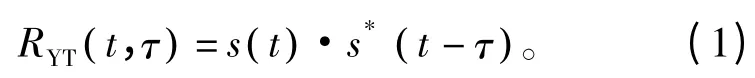
式中，s*(t) 为信号 s (t) 的共轭，τ 为延迟量。

定义2 信号瞬时自相关函数［9］。它是信号的同相分量和正交分量的乘积，记为

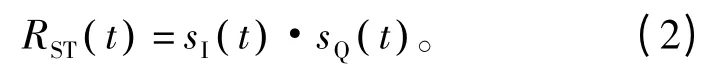
式中，sI(t)、sQ(t) 分别为信号的同相分量和正交分量。

设接收信号为

则其延迟相关为

式中，噪声 n (t) 与信号无关，且当τ ≠0 时，

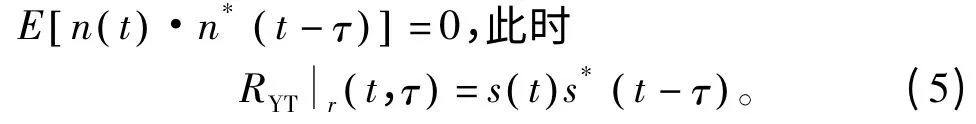
而对于瞬时自相关函数，由Hilbert 变换的性质可知，同相分量和正交分量的相位相差90°，即可以视为四分之一周期的延迟，即τ0=T/4，T 为信号周期，此时

由上面推导可看出，对信号进行延迟相关和瞬时自相关处理都能有效降低噪声的影响，为之后提取识别特征提供较好的信噪比条件。

3 基于信号相关特性的识别方法

通信中较多使用的调制方式为2ASK、BPSK、QPSK、2FSK 和4FSK，以这5 种信号作为待识别信号集，从中任选两种信号组成时频重叠双信号，则可以构成15 对信号。

在信噪比为0 dB时，各信号时频重叠时的频谱图如图1 所示。

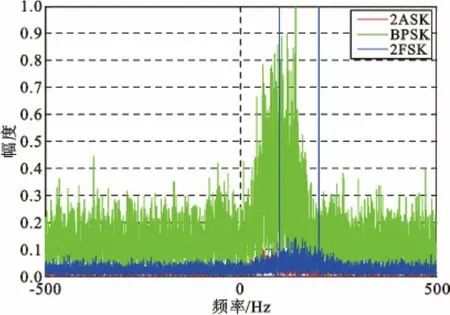
图1 各信号时频重叠时的频谱图Fig.1 Spectrum of time－frequency overlapped signals

对于单信道时频重叠双信号而言，y (t)=s1(t) +s2(t)，结合式(8)～(10)，代入式(1)和式(2)可推得6 类信号组合的延迟相关和瞬时自相关函数分别如式(11)～(16)所示。

令FYT(f)=，其 中E［·］t是对t 取期望，则从式(11)～(16)可看出，利用延迟相关值序列的频谱谱峰数(即谱峰数是否为1)可以将6 类信号组合分成两类:{ASK +ASK、ASK+PSK、ASK +FSK}和{PSK +PSK、PSK +FSK、FSK+FSK};而表1 为各种时频重叠信号延迟相关值序列频谱归一化最大值(即真实谱峰幅度)的理论值，表2 为各种时频重叠信号瞬时自相关值序列频谱归一化最大值的理论值，结合两者可以区分多种信号。

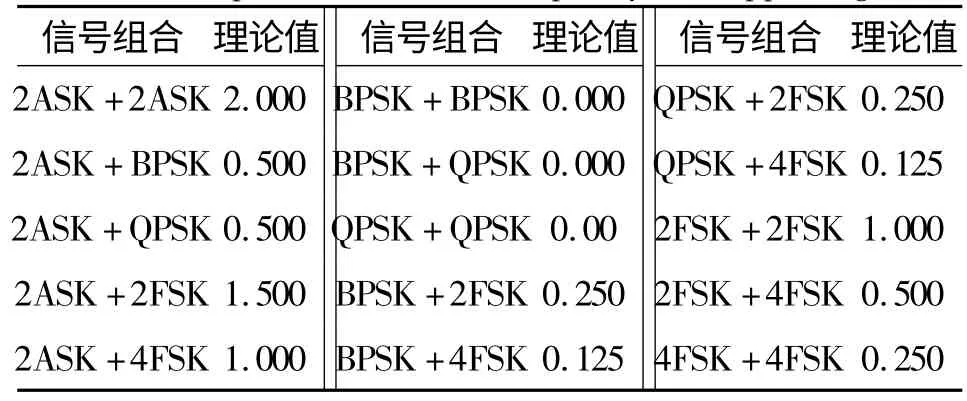
表1 各种时频重叠信号延迟相关值序列频谱归一化最大值的理论值Table 1 Theoretical normalized maximum value of delay correlation spectrum of time－frequency overlapped signals

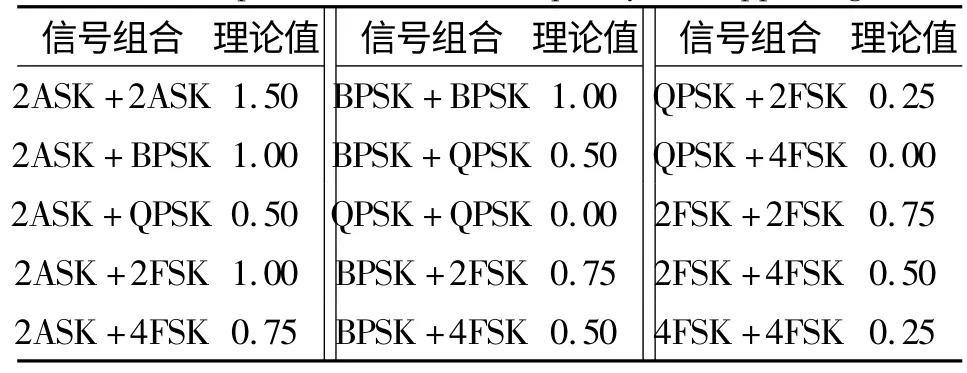
表2 各种时频重叠信号瞬时自相关值序列频谱归一化最大值的理论值Table 2 Theoretical normalized maximum value of instantaneous correlation spectrum of time－frequency overlapped signals

构造特征向量η0=[N，D，M]，其中N 为延迟相关值序列的频谱谱峰数，D 为延迟相关值序列频谱归一化最大值，M 为瞬时自相关值序列频谱归一化最大值。由上述分析可以看出，此特征向量可以将15 种时频重叠信号区分开，但考虑到噪声影响，PSK+PSK 和BPSK +4FSK、QPSK +4FSK 的区分不够明显，故引入特征参数T，定义为延迟相关值序列谱峰位置的方差，形成新的特征向量 η1=[N，D，M，T ]。由于PSK+PSK 形成的谱峰为调制信号产生的虚假峰，故其方差较小，而FSK 产生的谱峰为载频产生的峰，其方差较大，故T 可以有效区分开PSK+PSK。

4 仿真实验及分析

为验证所提理论和算法的有效性，利用MATLAB 进行了相关的仿真验证。考虑到参数设置的合理性以及仿真程序的速度等，不失一般性地设定:信号载频为100 Hz，FSK 信号频率集为{100，150，200，250}，采样频率为1000 Hz。信源长度为256 个码元，噪声为理想高斯白噪声。时频重叠信号的码速率分别为50 b/s和100 b/s，功率比为1∶ 1。

(1)实验1:仿真第一个特征参数N

计算15 种时频重叠信号延迟相关值序列的频谱谱峰数。由图2 可看出，ASK +ASK、ASK+PSK和ASK+FSK 三类信号谱峰数为1，其余均大于1，与理论分析相符。

图2 延迟相关值序列频谱谱峰数Fig.2 Peaks account of delay correlation spectrum(Para N)

(2)实验2:仿真第二个特征参数D

计算15 种时频重叠信号的延迟相关值序列的频谱归一化最大值。由图3 可以看出，这15 种信号的仿真结果和理论分析相符。

图3 延迟相关值序列频谱归一化最大值Fig.3 Normalized maximum value of delay correlation spectrum(Para D)

(3)实验3:仿真第三个特征参数M

计算15 种时频重叠信号的瞬时自相关值序列的频谱归一化最大值。由图4 可以看出，这15 种信号的仿真结果和理论分析相符。

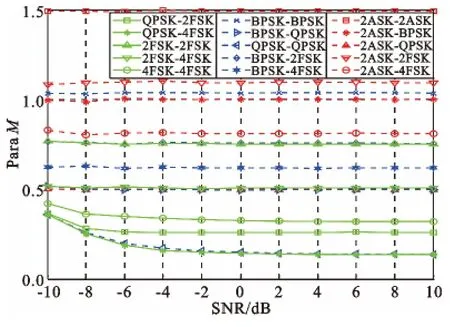
图4 瞬时自相关值序列频谱归一化最大值Fig.4 Normalized maximum value of instantaneous correlation spectrum(Para M)

(4)实验4:仿真第四个特征参数T

计算PSK+PSK、BPSK +4FSK 和QPSK +4FSK信号的延迟相关值序列频谱谱峰位置方差。由图5可以看出，PSK+PSK 类的值最小，约为0.105，而其余两种信号的值约为0.193。

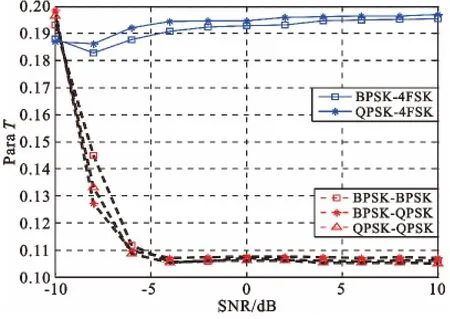
图5 延迟相关值序列频谱谱峰位置方差Fig.5 Peaks locations' variance of delay correlation spectrum(Para T)

(5)实验5:验证本文方法在理想高斯白噪声背景下的性能

基于特征向量η1=[N，D，M，T ]，并采用前4 个实验获得的最佳阈值，使用易于理解实现的决策树［10］方法进行识别分类，识别流程如图6 所示，步骤如下:

步骤1:分别计算信号延迟量为{τ1，τ2，…，τk}点的延迟相关值{Y (t，τ1)，Y (t，τ2)，…，Y (t，τk)}，计算其延迟相关谱峰数N，将待识别信号分成两类:(ASK+其他)和(PSK+PSK/ PSK+FSK/ FSK+FSK);

步骤2:对于判别类属于(ASK +其他)的信号，计算其延迟相关频谱归一化最大值D，将待识别信号分成4 类:2ASK +2ASK、2ASK +2FSK、2ASK +PSK 和2ASK+4FSK;

步骤3:对于判别类属于(PSK+PSK/ PSK +FSK/ FSK+FSK)的信号，计算其延迟相关频谱归一化最大值D，将待识别信号分成4 类:2FSK +2FSK、2FSK+4FSK、(4FSK +4FSK/BPSK +2FSK/QPSK +2FSK)和(PSK+PSK/BPSK+4FSK/QFSK+4FSK);

步骤4:对于判别类属于(4FSK+4FSK/BPSK+2FSK/QPSK+2FSK)的信号，由延迟相关谱峰数N可将其分为两类:4FSK +4FSK 和(BPSK +2FSK/QPSK+2FSK);

步骤5:对于判别类属于(PSK+PSK/BPSK +4FSK/QFSK+4FSK)的信号，由延迟相关值序列频谱谱峰位置方差T 可将其分为两类:PSK +PSK 和(BPSK+4FSK/QPSK+4FSK);

步骤6:对于判别类属于2ASK+PSK 的信号(属于(BPSK +2FSK/QPSK +2FSK)的信号、属于(BPSK+4FSK/QPSK +4FSK)的信号、属于PSK +PSK 的信号)，由一阶瞬时自相关频谱归一化最大值M 可将其分类。

图6 信号识别算法流程图Fig.6 Flow chart of signal recognition algorithm

每种信号在每个信噪比下进行2000 次独立Monte Carol 测试，信噪比从－10～10 dB(2 dB 步进)，识别效果如图7 所示。

实验表明，对于这15 种时频重叠信号，当全频段信噪比(可分析带宽为－ 500～500 Hz)大于－5 dB时，整体识别正确率大于95%。

在之前所设置的仿真条件下与已有算法相比，表3 给出了3 种不同算法的识别类型和平均识别效果。由于基于循环平稳特性的方法容易受不同信号特征交叠的影响，故其可识别类型较少，且低信噪比下识别效果较为一般。从对比结果也可以看出，本文可识别的调制类型比较多，且整体识别效果更好。

图7 各信号识别效果图Fig.7 Comprehensive recognition effect

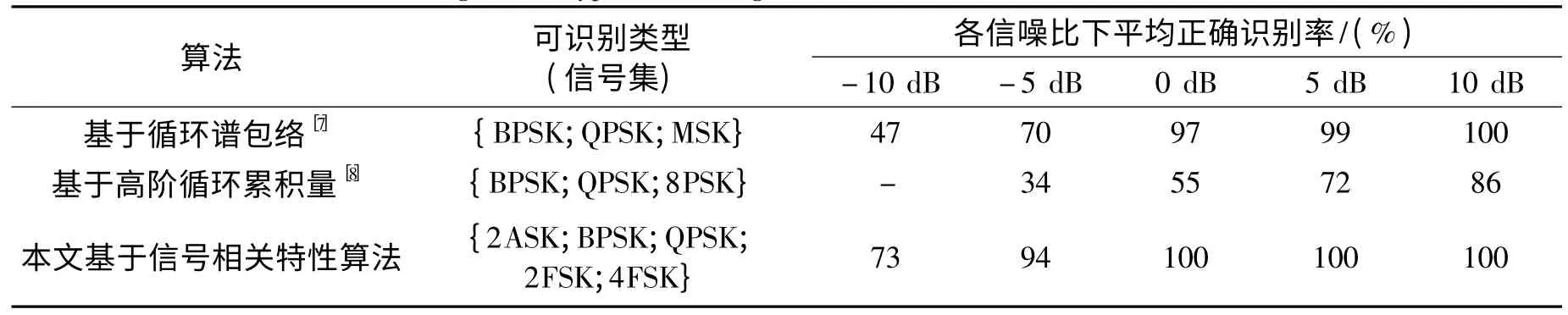
表3 不同方法的识别类型和识别效果Table 3 Recognizable types and recognition effect of different kinds of methods

5 结束语

本文提出了基于信号相关特性的单信道时频重叠信号调制识别方法，通过对信号进行延迟相关和瞬时自相关处理，对功率比为1∶ 1 情况下的同载频不同带宽单信道时频重叠双信号进行调制识别，有效解决了常见识别方法可识别类型少和低信噪比下效果一般的问题，但对于时频重叠多信号、同带宽不同载频情况下、功率不同时的时频重叠信号的调制识别还需进一步研究。

［1］付仕平，杨丽，邵伟.基于瞬时特征参数的数字信号调制识别算法［J］.现代防御技术，2013，41(6):71－75.FU Shiping，YANG Li，SHAO Wei.Digital Signal Modulation Classification Algorithm Based on Instantaneous Parameter［J］.Modern Defence Technology，2013，41(6):71－75.(in Chinese)

［2］Zhou Z Y，Chen H，Liu N N.Automatic recognition of multiple interferences and signals in the same channel based on ICA［C］// Proceedings of 2009 IET International Radar Conference.Guilin:IEEE，2009:1－4.

［3］王立东，张晓林，孔挺.基于ICA 和SVM 的混合通信信号调制方式识别［J］.仪器仪表用户，2011，18(2):62－65.WANG Lidong，ZHANG Xiaolin，KONG Ting.Mixed Communicaiton Signals Modulation Mode Identification Based on ICA and SVM［J］.Electronic Instrumentation Customer，2011，18(2):62－65.(in Chinese)

［4］杜宇.多信号调制识别算法研究［D］.哈尔滨:哈尔滨工程大学，2013.DU Yu.Research on Modulation Recognition Algorithm for MultipleSignals［D］.Harbin:Harbin Engineering University，2013.(in Chinese)

［5］朱波.基于小波的单信道时频重叠信号参数分析与实现研究［D］.成都:电子科技大学，2010.ZHU Bo.Research on the Parameter Analysis and Implementation for Signle－channel Time－frequency Overlapped Signal Based on Wavelet［D］.Chengdu:University of Electronic Science and Technology of China，2010.(in Chinese)

［6］Omara Y，Grajal J.Cyclostationarity Based on a Single Sensor［C］// Proceedings of 2008 Radar Conference.Rome:IEEE，2008:1－6.

［7］余志斌，于宁宇.基于循环谱包络的多信号调制识别［J］.计算机应用，2012，32(8):2119－2122.YU Zhibin，YU Ningyu.Modulation Recognition for Multi－component PSK Signals Based on Cyclic Spectrum Amplitude［J］.Journal of Computer Applications，2012，32(8):2119－2122.(in Chinese)

［8］李旷代，郭黎利，石荣，等.单信道时频重叠MPSK 信号的调制识别方法［J］.火力与指挥控制，2010，35(2):150－153.LI Kuangdai，GUO Lili，SHI Rong，et al.Modulation Recognition Method for Single－ Channel Time－ Frequency Overlapped MPSK Signals［J］.Fire Control ＆ Command Control，2010，35(2):150－153.(in Chinese)

［9］Zhou M，Feng Q.A new feature parameter for MFSK/MPSK recognition［C］//Proceedings of the 2011 International Conference on Intelligent Science and Information Engineerin(ISIE).Wuhan:IEEE，2011:21－23.

［10］徐毅琼.数字通信信号自动调制识别技术研究［D］.郑州:解放军信息工程大学，2011.XU Yiqiong.Research on Automatic Modulation Recognition of Digital Communication Signals［D］.Zhengzhou:PLA Information Engineering University，2011.(in Chinese)