偏馈法距离校零误差校正*

杜 丹

(中国西南电子技术研究所，成都 610036)

1 引言

测控站距离校零的传统方法是反测法，即利用已知距离的远场区标校塔获得地面设备的零值［1］。由于测量精度高、系统误差小，对塔校零的方法得到了长期应用。以往，偏馈法［2］作为距离校零的辅助手段，主要采用零值分离，记忆系统零值变化并加以修正［3］，与海上桅杆标校的过程相似，常用于稳定性检查［4］，本身的距离残差并不是重点。近年来，由于场地条件的限制，越来越多的测控站采用无塔标校的方式，这就对偏馈法距离校零的精度提出了更高的要求。

偏馈法将校零天线安装在主反射面，通过无线的方式构成系统射频闭环，校零天线位于主天线口面场内，近场引起时延误差，多径产生泄露误差［5］，文献［6］列出了这两项误差的模拟计算结果，总误差不超过0.6 m，而工程实测结果却显示校零误差有超过10 m的情况［6］。文献［6］指出，利用偏馈法计算地面设备的距离零值时，需要引入一个修正量，因此偏馈法距离校零存在模型误差，且为主要误差分量，但文献［6］并未明确修正量的具体含义和计算方法，其他文献也未见相关的表述。

本文首先通过一次试验提出偏馈校零产生的误差，以此为基础，从几何的角度系统地分析偏馈校零和对塔校零的差异，明确产生误差的根本原因，并建立数学模型，使两种工作方式的距离零值完全等效。试验结果证明了误差校正的正确性。

2 偏馈法距离校零的试验误差

距离校零测量的是电磁波传播的几何路径，不管是采用标校塔的方法校零，还是采用偏馈的方法校零，都要涉及到几何路径的扣除。某次试验利用12 m天线S 频段测控系统进行距离校零，以对塔校零为参考，研究偏馈校零的测量误差，试验方法和几何路径如图1 所示。

图1 对塔校零和偏馈校零试验方法Fig.1 Expriments of zero range calibration by feed set－off and by tower

2.1 对塔校零的试验结果

试验首先将校零天线和校零变频器架设到远场标校塔，控制测站天线对准校零天线完成测距。试验前，测距终端未作任何调整，中频闭环的距离零值为4 672 095.5 m，仪器标定校零变频器(包含电缆)的零值为23 m。对塔测距结果为4 677 174.55 m，试验前，塔距R0SP已经过准确测量为2479 m，用于地面设备零值的计算

式中，R0SP为天线三轴中心到标校塔校零天线的空间距离，R0ZRT为校零变频器零值，R0∑为终端测距值，R0G即三轴中心到测距单元的地面设备零值。

2.2 偏馈校零的处理模型和测量误差

试验第二步将相同的校零天线架设到测站天线的主面上，采用偏馈法在中强电平的条件下完成测距，测距的结果为4 672 226.77 m。校零变频器(包含电缆)相同，其零值为23 m。

偏馈校零的信号路径如图1(b)所示，采用直接扣除的方法计算地面设备零值，扣除部分包括所有从三轴中心到校零变频器的设备时延及几何时延，相关几何尺寸如表1 所示。

表1 偏馈校零相关的几何尺寸Table1 Geometry size applied to zero range calibration by feed set－off

采用直接扣除的方法计算地面设备零值:

式中，R3、R4、R0F1和R0F2的定义如表1 所示，试验前已经准确测量;R0∑=4 672 226.77 m 为终端测距值;R0G即三轴中心到测距单元的地面设备零值。根据式(1)和式(2)，偏馈法距离校零与对塔校零的测量结果差13.55 m，不能满足系统的使用要求。这种处理方法的另一个问题是，对于R0F1和R0F2的测量，其操作性差且误差较大。

3 偏馈校零模型误差分析和校正

试验表明，偏馈校零采用直接扣除的方法计算地面设备零值存在较大误差，这种误差是处理模型引起的误差，需要系统地分析产生误差的原因，并建立新的模型以校正该误差。

3.1 模型误差分析

任务时，测距终端的测量值为航天器返回的下行信号与测控站发射信号之间的总延迟τ，包括了天、地设备零值和空间距离延迟之和，只有分别标定了天、地设备零值并扣除，才能计算出空间距离，测距的参考点选在天线方位轴和俯仰轴交点，这个点是固定的，可通过精密测绘获取坐标。而对塔测距的原理其实是相同的，只要将塔上的转发器视为与应答机等效即可。根据测距的基本原理，将对塔校零的信号路径作几何分解，其模型如图2 所示。

图2 对塔校零的几何模型及光程路径Fig.2 Geometric model and 0ptical path applied to zero range calibration by tower

对塔标校采用式(3)表示测距总时延、地面设备零值以及空间距离延迟的关系:

式中，τall为测距总时延，τAS为地面天线三轴中心A点到塔上天线S 处的电波传输时延，τSZ为地面设备距离零值，τt为塔上校零变频器时延。

对塔测距总时延分解如图3 所示。

图3 对塔测距总时延分解图Fig.3 Composition of delay in model of zero range calibration by tower

分析图2 中测距信号的几何路径，就会发现式(3)中的参数项τSZ与实际的地面零值存在差异，这种差异体现在塔距AS 和信号的光程路径AOHFE +BS 是不同的，测距总时延更为准确的表达式为

式中，τUP为信号经基带、上变频器、高功放、馈源直至副面焦点O 的上行时延，τDN为信号从副面焦点O经馈源、接收通道直至基带的下行时延，τOHFE为信号从副面焦点O 经副面、主面反射后到达天线等相位面处时延，τBS为信号从等相位面B 点传输到塔上校零天线S 点的时延。

重要的是，式(3)反映的正是两个逆向过程的内在关系，即对塔校零和对航天器测距，它们的表达式可以完全相同，而过程是反向的。对塔校零是已知空间距离计算地面设备零值，而对航天器测距是已知地面设备零值，计算空间距离。可见，两个过程的测距方法相同，空间距离的定义相同，地面设备零值的定义也完全相同，只不过是反向测量。因此，即使对塔标校得到的“设备零值”不是绝对的零值，却恰好能正确地应用于测距任务。图1 试验中，偏馈法距离校零时采用了式(2)直接扣除从三轴中心到校零变频器之间所有距离，获得的是距离“真值”，与任务中装订的“误差值”反而存在差异，需要对处理模型进行校正。

3.2 模型误差校正

同样对偏馈校零的信号路径作几何分解，其模型和光程路径如图4 所示。

图4 偏馈校零的几何模型及光程路径Fig.4 Geometric model applied to zero range calibration by feed set－off

采用式(5)表示偏馈法测距总时延、校零变频器零值以及空间距离延迟的关系:

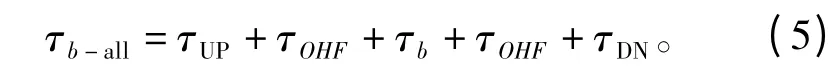
式中，τb－all为偏馈环路下测距总时延，τb为校零变频器时延，τOHF为信号从副面焦点O 经副面反射后到达偏馈天线处时延。

如前所述，式(3)中的参数项τSZ是带有“误差”的设备零值，也是实际任务中需要装订的零值，如果能够通过式(4)、(5)共有的参数τUP、τDN传递，代入到偏馈校零的表达式即式(5)中，就可以找到与偏馈测距总时延的正确关系，从而完成误差校正。

首先将式(3)代入式(4)，求τUP、τDN与τSZ的表达式为

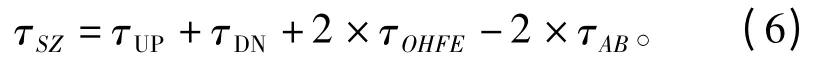
式中，τAB为图4 中A－B 段路径时延。再将式(6)继续代入到式(5)，求τSZ与τb－all的关系为

定义τFG为偏馈天线到三轴中心等相面的距离时延。根据式(5)，偏馈法距离校零的总时延分解如图5 所示。

图5 偏馈法距离校零总时延分解图Fig.5 Composition of delay in model of zero range calibration by feed set－off

因此，采用偏馈法距离校零的数学模型式(7)找到的τSZ就与对塔校零中的τSZ完全相同，此“设备零值”从物理意义上讲并不是“真值”，却恰好能正确地应用于测距任务，其与真值之间的误差就是图4 中OB 和OHFE 的几何路径差。分析图2，τSZ是在测距总时延中直接扣除塔距时延τAS，实际上少扣除了主副面之间的反射路径，即任务使用的τSZ比“真值”大一个误差量Δ:

前述的某次试验，校零天线架设在图1 中的位置P2，与式(7)中τFG对应的光程距离(如表1 的R5所示)为4.54 m;与式(7)中测距时延τb－all对应的是距离值，如上述试验值为4 672 226.77 m;与式(7)中校零变频器时延对应的距离值为23 m，根据式(7)的数学模型，代入对应的距离值，计算地面设备零值

式中，时延乘光速c 可得到对应的距离值。采用式(7)校正“误差”后，与式(2)相比，偏馈校零距离零值增加了14.69 m，与式(1)对塔校零的设备零值4 672 193.55 m仅相差1.14 m。

4 偏馈校零的近场误差

除了模型误差，偏馈法距离校零还有两项主要的近场误差，即时延误差和漏射误差。

时延误差是指口面场内，信号实际的物理时延不同于几何光学时延，如果仍然扣除几何时延计算地面设备的距离零值，就会带来误差。可采用辐射场分布的方法，对时延误差进行模拟计算，结果表明，口面场内随着校零天线位置的上移，时延误差逐渐减小，主面边缘时延误差最小，主面底部区域时延误差最大，但不超过30 cm［6］。

漏射误差主要是指馈源多径产生的传输路径误差，最简单的漏射模型不考虑馈源漏射的多次反射，只考虑馈源直接漏射到校零天线，如图6 所示。

图6 馈源漏射示意图Fig.6 Principle of center feed' s influence by mutipath

校零信号是沿ABC 路径到达校零天线的，而馈源的漏射信号直接沿AC 路径到达校零天线。由于多径矢量和引入附加相移，使测距时延发生变化，于是校零结果产生了误差。因此，漏射误差主要取决于多径信号的相对电平差，应尽量减小漏射信号的电平从而减小附加相移。显然，校零天线的安装位置及波束宽度是漏射误差的主要影响因素。口面边缘，校零天线位于馈源口的近角旁瓣或波束之内，漏射误差较大，而靠近主面底部的区域，校零天线位于馈源口的远角旁瓣，泄露信号与主反射信号的电平相差甚大，因此漏射误差最小。计算结果显示，口面场内，最大漏射误差不超过30 cm［6］。

综合考虑这两项近场误差，主面底部时延误差最大，但漏射误差却比其他位置成倍减少，使两项误差的总和更小，因此偏馈天线应该安装在靠近主面底部馈源辐射不到的地方。计算结果表明主面底部总误差最小约为33 cm，口面场内的最大误差约为60 cm［6］。

5 试验结果及分析

为了减小近场误差，调整偏馈天线的位置到P1点，如图1 所示，以主抛物面顶点为原点建立X、Y坐标系，用P(X，Y)表示偏馈天线在口面场内的位置，P1(0.4，2.5)点位于主面底部，与三轴中心的距离，即与式(7)中τFG对应的光程长度为R6=3.4 m。再次进行偏馈校零试验，测距值为 R=4 672 224.21 m，采用模型误差校正式(7)，计算地面设备零值

式 中，τb－all为测距时延，对应距离值 为4 672 224.21 m;τb为校零变频器时延，对应的距离值在试验前已经标定为23 m。与式(1)对塔校零的设备零值4 672 193.55 m相比，式(10)计算结果与其仅相差0.86 m。

如前文所述，模型误差是偏馈校零的主要误差，几何校正方法从机理上消除了该误差，但在实际操作过程中，不论是对塔校零还是偏馈校零，都存在一定的测量误差，如三轴中心到标校点的距离、校零天线与变频器之间的电缆延时，正是由于这两种方法的不同测量误差，导致互比结果的差异，工程上一般都在米的量级。本文以对塔校零作为参考，仅仅是为了方便分析和解决模型误差，而实际上使用的距离残差只是与理论值的差异，不会考虑对塔校零的测量误差，因此距离残差有可能更小。

口面场内，近场总误差最大不超过60 cm，最小约30 cm，确定偏馈天线的安装位置到主抛物面底部馈源辐射不到的地方，最大修正误差可达到30 cm，因此在几何校正的基础上，误差可进一步减小到1 m以内。

6 结束语

由于场地条件，越来越多的地面测控站采用了偏馈法距离校零。相关文献多从零值分离的角度论述了偏馈法的应用，对于无塔条件下只能采用偏馈法距离校零及其误差则关注较少，文献［6］指出偏馈法需要修正，但并未明确分析和给出计算方法。本文提供的校正方法简单易用，与传统对塔校零相比误差约1 m，不难满足校零残差要求为3 m的中精度测量系统。本文的几何校正方法对测控领域的无塔标校具有参考价值，如果能够建立更复杂和精细的近场仿真模型，误差能进一步减小，可以用于更高精度的测量系统。

［1］赵业福.比相测距系统天、地零值校准(上)［J］.飞行器测控学报，2001，20(1):27－35.ZHAO Yefu.Calibration Method of Phase－ comparing Ranging System(Part 1)［J］.Journal of Spacecraft TT＆C Technology，2001，20(1):27－35.(in Chinese)

［2］文龙，龙斌，陈颖.一种无塔校准方法研究［J］.计测技术.2007，27(4):39－64.WEN Long，LONG Bin，CHEN Ying.Research on a Kind of Tower－less Calibration Method［J］.Metrology ＆ Measurement Technology，2007，27(4):39－64.(in Chinese)

［3］杨卫平，王俊，杨奇.一种提高活动站无塔距离校零设备可靠性的方法［J］.电光系统，2013(2):25－26.YANG Weiping，WANG Jun，YANG Qi.AMethodsfor Improving the Reliability of Non－tower Range Zero Value Calibration Equipment for Movable TT＆C Station［J］.Electronic and Electro－optical Systems，2013(2):25－26.(in Chinese)

［4］周江，候辉，段庆光.小频偏直接距离校零法原理与应用分析［J］.电讯技术，2004，44(1):87－90.ZHOU Jiang，HOU Hui，DUAN Qingguang.Basic Principles and Application of the Direct Range Zeroing by Means of Little Frequency Excursion［J］.Telecommunication Engineering，2004，44(1):87－90.(in Chinese)

［5］邱冬冬，鲁新龙，金华松.测控雷达距离零值校准方法研究［J］.现代电子技术，2012，35(17):36－38.QIU Dongdong，LU Xinlong，JIN Huasong.Methodsof Zero Range Calibration for Shipborne，TT＆C Radar［J］.Modern Electronics Technique，2012，35(17):36－38.(in Chinese)

［6］赵业福.比相测距系统天地零值校准(下)［J］.飞行器测控学报，2001，20(2):22－28.ZHAO Yefu.Calibration Method of Phase－ comparing Ranging System(Part 2)［J］.Journal of Spacecraft TT＆C Technology，2001，20(2):22－28.(in Chinese)