趣味教学法在高等数学教学中的应用
2015-12-24齐雪
齐 雪
趣味教学是将学生感兴趣的问题或者实际生活中遇到的问题融入到课堂教学中,通过这些问题引出教学知识,解决教学问题,使抽象的知识得到具体的应用。本文将趣味教学应用于大学数学教学中,激发学生的学习兴趣,提高课堂教学质量,促进学生全面发展。趣味教学主要是激发学生的求知欲,使学生进入问题情境,从而产生好奇心,形成探究愿望[1]。这对提高学生的专业素养,培养高素质应用型人才具有十分重要的意义。下面以几个知识点为例,介绍趣味教学在高等数学教学中的应用。
一、函数概念中的趣味教学
大学生在中学已经接触过函数概念,也可以用函数分析一些实际问题,所以,作为复习内容,可以提出一些实际生活中应用函数进行分析计算的例子。如话费升降问题、涨跌停板问题、库存问题、军备竞赛问题,等等。
以话费升降问题为例[2],我国的电信资费有一次结构性的调整,调整前某地区固定电话的市话费为每3分钟 (不足3分钟的以3分钟计算)0.18元,调整后前3分钟0.22元,以后每1分钟(不足1分钟的以1分钟计算)0.11元。那么,与调整前相比,市话费是降了还是升了?升、降的幅度是多少?接下来,老师要引导学生分别建立调整前、后话费与通话时间之间的函数关系。
调整前,话费y(t)与通话时间t之间的函数关系为:

调整后,话费Y(t)与通话时间t之间的函数关系为:
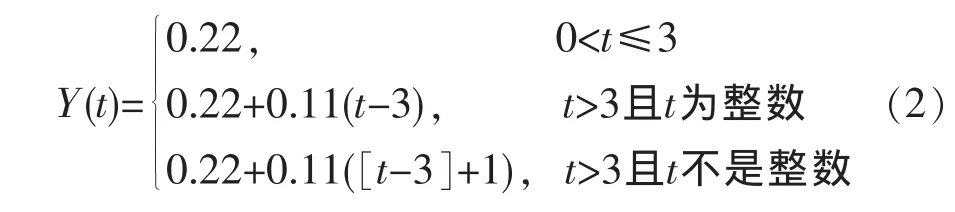
为了分析话费的升降情况,可以列表进行比较。
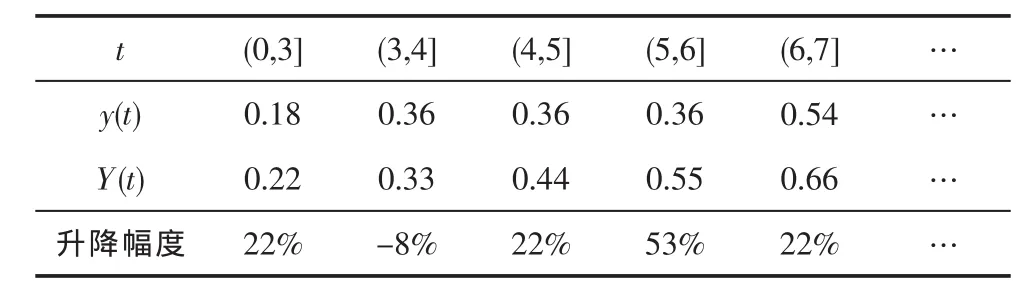
表1 话费升降情况
从表 1看出,只有当通话时间 t∈(3,4]时,调整后的话费才有所降低,其余的时段均比调整前有较大幅度的提高。
由此例可以帮助学生回忆与函数相关的知识。如自变量与因变量的关系可以用方程来表示分段函数的特点和性质、变化幅度的计算等问题。教师可以此为出发点,将函数知识进行系统的复习。
二、极限知识中的趣味教学
极限概念的数学定义抽象难懂,学生学习起来有些困难,为了使极限的概念形象生动易于理解,可以结合一些生活实例进行讲解。如1906年数学家科赫提出了描述雪花形状曲线的方法:将一条线段三等分,先以中间的一段为底边做一个正三角形,然后再去掉这个正三角形的底边,可得到一条由4条长度为原线段长度1/3的线段构成的折线,如果对构成这条折线的每一条线段不断重复上述的步骤,得到的曲线就是“科赫曲线”[3]。
下面,做一个边长为a的正三角形,然后在这个三角形的每条边上不断重复上述的变换,便可以得到科赫雪花图案。若以Cn、Sn分别表示第n步变换后的科赫雪花的周长和面积,则周长依次为:
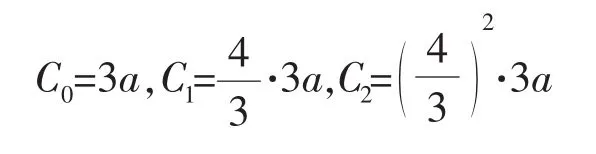
由数学归纳法得:
Cn面积依次为:
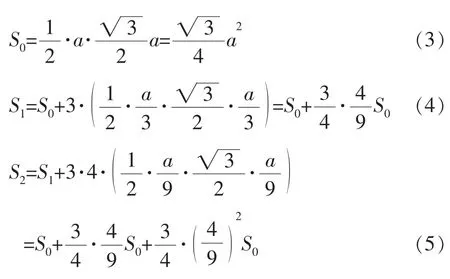
由数学归纳法得:
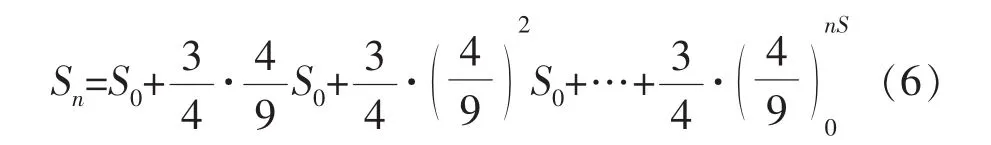
观察Cn和Sn的变化趋势,判断当n→∞时,Cn和Sn取值的趋向情况,进而引入数列极限的概念,通过这一节知识的学习来解决上述问题。于是,得到:
上述结果表明,科赫雪花图案的面积是有限的,但周长却趋于无穷大[4]。
由此例,学生们可以更加形象直观地了解数列极限,对后续函数极限、极限性质、极限计算等知识的学习也具有启发作用。
三、级数知识中的趣味教学
级数知识是高等数学的重要内容之一,它是研究函数性质和进行数值计算的有力工具[3]。下面通过一个有趣的例子引出级数概念,并利用级数知识解决相关问题。
古希腊著名哲学家Zeno曾经提出一个悖论[5]:先让乌龟爬行一段距离,然后再让古希腊神话中善跑的英雄阿基里斯去追赶乌龟,那么阿基里斯是永远也追不上乌龟的。Zeno提出此悖论的依据是:阿基里斯若想追赶上乌龟,必须先到达乌龟的出发地点,而在这段时间内,乌龟又向前爬行了一段距离,于是,阿基里斯必须赶上这段距离……如此分析下去,虽然阿基里斯离乌龟越来越近,但却永远也追不上乌龟。后来有人把Zeno的这个悖论移植到“龟兔赛跑”问题中,声称兔子永远也追不上乌龟。这个结论显然是错误的,但这种推理在逻辑上却没有问题,那么,问题究竟出在哪里呢?
下面,我们从数学的角度来分析这个问题。设兔子和乌龟的速度分别是V和v( V>> )v,如果兔子是在乌龟已经爬过距离s1后开始追乌龟的,那么在兔子跑完距离s1的时间之内,乌龟又爬行的距离s2为:

而在兔子跑完s2的时间之内,乌龟又爬行的距离s3为:

以此类推,可知兔子需要追赶的全部路程S为:
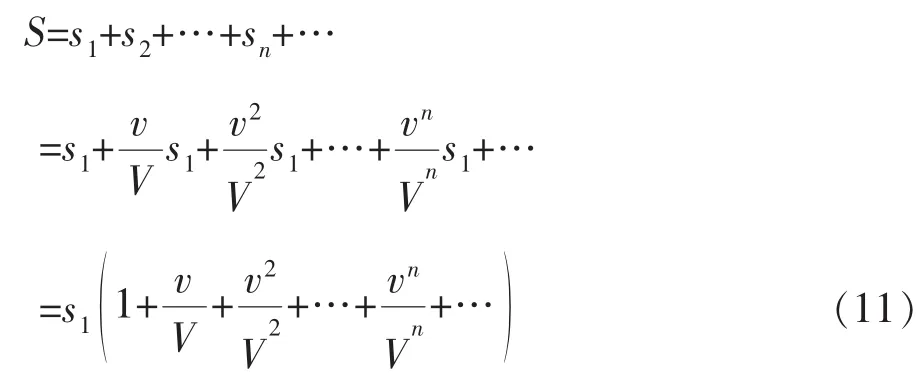
要想得到S的具体数值,就要引入级数概念,通过级数知识的学习,对S进行计算和分析。分析结果:S是一个公比的等比级数,它的和即兔子只要从起点跑稍微超过s1不多的一点距离就能很快追上乌龟。
四、趣味教学应把握的原则
为使趣味教学收到良好的教学效果,教师在对引例进行筛选时要把握以下原则:
(1)针对性。即,引例要与所介绍的高等数学知识紧密相关;
(2)难度适中。即,引例的分析、求解要易于理解;
(3)趣味性。即,引例要能引起学生的求知欲、探索欲;
(4)典型性。即,引例要有代表性,要正确、合理。
趣味性引例只是趣味教学法的一个有力工具,教师的个人魅力、教学风格、教学形式也是趣味教学法的重要因素。我们要在教学过程中积极思考、探索、丰富和发展趣味教学法,以此使高等数学教学更加生动有趣、更加充满魅力,从而提高教学质量和水平。
[1]曹炜萍.数学中的趣味教学[J].科教文汇(下旬刊),2009(11).
[2]李心灿.高等数学应用205例[M].北京:高等教育出版社,1997.
[3]李天胜.微积分[M].成都:电子科技大学出版社,2008.
[4]吴振奎.漫画分形[J].中等数学,1998(3).
[5]沈继红,施久玉,高振滨,等.数学建模[M].哈尔滨工程大学出版社,1996.
