SCR 蜂窝状脱硝催化剂磨损数值模拟研究

徐秀林，吴卫红，柳东海，郑成航，施正伦，高翔

(浙江大学 能源清洁利用国家重点实验室，浙江杭州 310027)

选择性催化还原(SCR)烟气脱硝工艺作为目前脱硝的主流技术，市场占有率约为95%［1］，其中催化剂是SCR 脱硝技术的核心，但是受到工艺布置位置和煤质的影响，容易造成催化剂的过度磨损，严重时引起催化剂坍塌，造成SCR 脱硝活性下降，使用寿命缩短。因此，研究蜂窝状SCR 脱硝催化剂的磨损问题，对延长催化剂的使用寿命，减少环境问题具有一定的指导意义。

随着计算流体力学的发展，数值模拟研究成为材料磨损研究的有用工具，国内外许多学者对气固两相流中颗粒与壁面的碰撞和磨损问题进行了研究［2-6］。何文深等［7-9］通过实验的方法对催化剂的磨损行为进行了研究，取得了一定进展，但不能完全反应催化剂磨损情况。因此，数值模拟方法作为催化剂磨损研究的一种重要工具，对揭示催化剂的磨损特性、磨损规律、磨损机理具有十分重要的意义。

本文采用Ansys Workbench 软件，将数值模拟方法应用到催化剂磨损分析上。笔者前期已对烟气流速、粉尘浓度、粉尘粒径等因素进行了研究，本文将重点围绕催化剂孔径大小、多层布置方式、催化剂孔道堵塞等实际问题展开讨论，揭示催化剂磨损规律，为工程实践提供指导性作用。

1 数值模拟方法

1.1 计算区域

采用3 ×3 孔道催化剂作为模拟对象，催化剂长度方向取值为200 mm，同时为了分析催化剂端部和尾部的磨损情况，在模型前部各增加10 mm，图1 分别是不同孔径、不同布置间距和孔道堵塞研究模型。

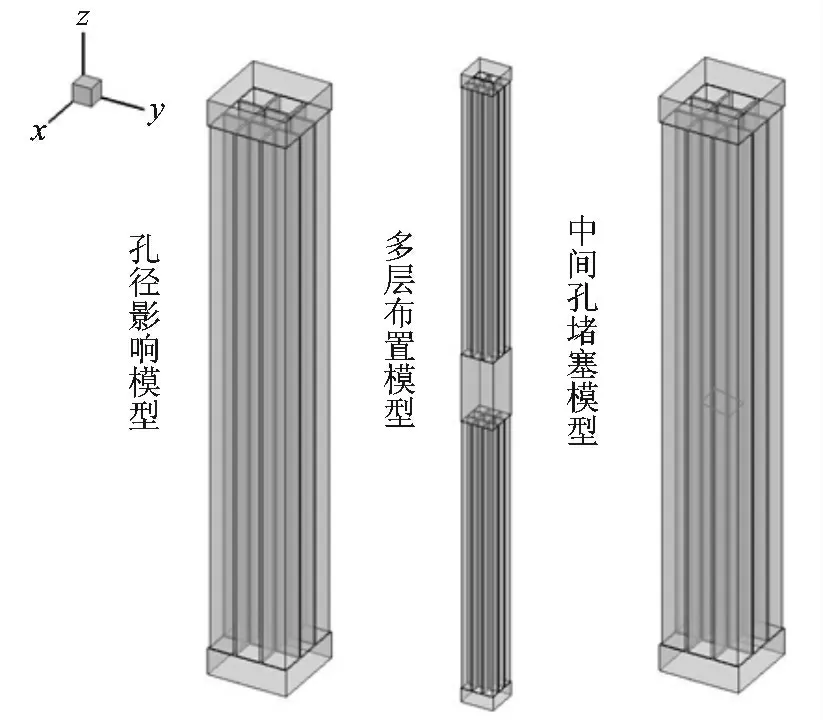
图1 催化剂几何模型Fig.1 Geometry model catalyst

1.2 气体运动模型

流场采用SIMPLE 法求解雷诺平均法NS 方程，湍流模型采用标准k-ε 模型，壁面函数采用标准壁面函数，整个流场区域的无量纲不可压缩流体控制方程为:

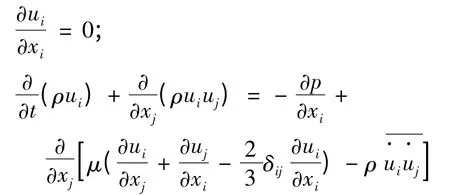
式中，ρ 为流体密度，ui、uj为流体速度，xi、xj是流场长度，p 为压力，μ 为流体粘度，δij为应力系数，ρ为未知雷诺应力分量;其中i，j=1，2，3。

1.3 颗粒运动模型

本文中粉尘颗粒作为稀疏相来考虑，采用拉格朗日轨道模型计算颗粒的运动轨迹，并考虑了颗粒与流体之间的双向耦合。由于粉尘是稀疏相，本文忽略了颗粒之间的相互碰撞以及颗粒自身的旋转。颗粒的运动方程为:

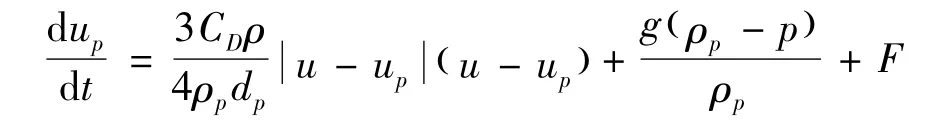
其中，up颗粒的运动速度，u 流体的运动速度，CD曳引系数，ρ 流体密度，ρp颗粒密度，dp颗粒直径，g 重力加速度，F 颗粒单位质量受到的其他外力。

本文中颗粒与壁面的碰撞模型和FAN 等［2］研究中一致，颗粒与催化剂壁面碰撞时的法向和切向恢复系数如下:

式中，Vn1、Vn2和Vt1、Vt2分别为碰撞前后法向和切向的速度，β1为颗粒与催化剂壁面碰撞时颗粒入射角度。

1.4 磨损模型

催化剂端面和孔道壁面受烟气中粉颗粒的撞击、冲刷，造成表面材料流失，磨损机理分别属于高角度和低角度冲蚀，本文结合Finnie I［10］的微切屑理论和Levy A［11］的薄片剥落磨损理论，分析催化剂磨损，其中催化剂磨损率定义为:

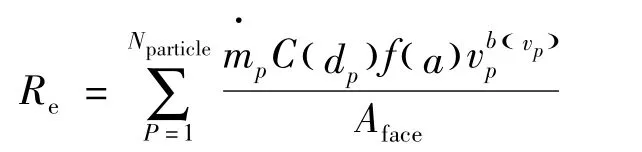
式中，Re为磨损率，Nparticle为颗粒数，为颗粒的质量流率，C(dp)为颗粒直径的函数，f(a)为入射角的函数，b(vp)为与颗粒碰撞速度相关的函数，Aface壁面计算单元面积。

其中函数C(dp)、f(a)、b(vp)，根据文献［12-16］分别选取为:

f( )a = X cos2αsin(wα)+Y sin2α，X 取0，Y 为常数;

b(vp)= n，n 为常数。

2 结果与讨论

2.1 不同孔径对催化剂磨损的影响

图2 和图3 是不同孔径下催化剂端面、孔壁磨损率的趋势图和孔壁磨损的对比图。

由图2 可知，催化剂孔径大小对催化剂端面磨损率影响不大，孔径从5 ～13 mm，催化剂磨损率基本维持在3.54 ×10－4～3.69 ×10－4kg/(m2·s);催化剂孔径大小对催化剂孔壁磨损率影响较大，磨损率随孔径的增大而减小，孔径为5 mm 时的磨损率最大Re= 4.46 ×10－6kg/(m2·s)，当孔径增大到13 mm 时，磨损率减小到1.23×10－6kg/(m2·s)，孔径5 ～9 mm 的催化剂磨损率下降趋势较快;当孔径大于9 mm 以后，磨损率下降趋势放缓。

图2 孔径尺寸对催化剂磨损的影响Fig.2 Influence of pore size on catalyst erosion

图3 不同催化剂孔径下孔壁磨损对比图Fig.3 Comparing pore wall erosion rate at different pore size

由图3 可知，不论孔径如何变化，催化剂孔壁的磨损分布和磨损率增长趋势基本相同:催化剂孔壁的磨损主要发生在催化剂的中后部，在催化剂入口附近的区域，壁面磨损率几乎为零;在L =25 mm处，磨损率开始增加，到100 mm 以后，增长趋势放缓，越往后磨损率几乎维持不变。同时沿孔道流速方向(除入口附近)任何一点的壁面磨损率随孔径的增大而减小，Re(D=7)＞Re(D=9)＞Re(D=13)。

根据文献［7-8］，催化剂的磨损主要受空速和局部粉尘浓度的影响。由图4(催化剂孔道内的速度分布图)和图5(催化剂孔道内颗粒浓度的分布图)可知，在相同边界条件下(d = 15. 96 μm、η =50 g/m3、u=15 m/s)，无论催化剂孔径大小，催化剂端面的颗粒浓度和对壁面的冲蚀速度几乎相同，因此孔径的大小对催化剂端面磨损率影响较小;在催化剂孔道内(图5)，不同孔径条件下颗粒浓度分布情况大致相同，但由图4 可知，随着孔径的增大，孔道截面处的速度梯度增加，孔径越大，孔道近壁处的流速相对越小，因此催化剂孔壁磨损率随催化剂孔径的增加而减少。

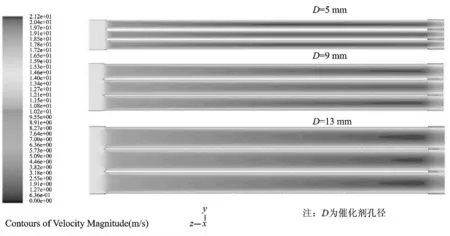
图4 催化剂孔道内的速度云图Fig.4 Velocity contours in catalyst pore

图5 催化剂孔道内的颗粒分布图Fig.5 Particle distribution in catalyst pore

2.2 多层布置的间距对催化剂磨损的影响

催化剂多层布置时，布置间距对第2 层催化剂磨损的影响见图6。

图6 多层布置间距对第2 层催化剂磨损的影响Fig.6 Influence of layer space on second catalyst erosion

由图6 可知，第2 层催化剂端面的磨损率随布置间距的增加而增加，但增长率随布置间距的增加逐渐变小，当布置间距S 超过150 mm 时，端面磨损率几乎保持不变，维持在3.50 ×10－4kg/(m2·s)左右，与第1 层催化剂的端面磨损率相当;第2 层催化剂孔壁的磨损率与布置间距成反比，间距越小，孔壁磨损率越大，但当布置间距S 超过150 mm 时，孔壁磨损率几乎保持不变，维持在2.62 ×10－6kg/(m2·s)左右，与第1 层催化剂的孔壁磨损率2. 46 ×10－6kg/(m2·s)几乎相等。

不同布置间距催化剂孔壁磨损率的对比见图7。

图7 布置间距对第2 层催化剂孔壁磨损的影响Fig.7 Influence of layer space on second catalyst pore erosion

由图7 可知，布置间距为10 mm 时的孔壁点磨损率大于布置间距为100 mm 的孔壁点磨损率，并且催化剂前部磨损率的差距较大;同时布置间距越大，第2 层催化剂孔道内的磨损分布越趋近于第1层催化剂的孔壁磨损分布:入口附近区域的壁面磨损为零，随后增加，到一定距离后增长趋势放缓，越往后磨损率几乎维持不变。由图8 可知，不同布置间距条件下，催化剂端面和孔壁磨损率变化趋势主要是由催化剂流域内粉尘颗粒的分布引起的。在催化剂端面，当催化剂布置间距较小时，由于前1 层催化剂的整流作用还没消除，颗粒在惯性作用下继续沿孔道方向移动，与第2层催化剂端面发生碰撞的粉尘颗粒数量较少，导致端面磨损较小;当催化剂布置间距逐渐增大，流体的湍流作用加强，粉尘颗粒向四周扩散，引起第2 层催化剂端面磨损率增加。相反，在催化剂孔道内，当催化剂布置间距较小时，间距内的粉尘颗粒运动轨迹变化较小，粉尘颗粒在第2 层催化剂孔道内的分布与第1 层催化剂后部孔道内分布相近，因此孔壁磨损率较大;当催化剂布置间距逐渐增大，第2 层催化剂入口前部的流场和颗粒分布逐渐趋向均匀，导致第2 层催化剂入口作用增强，引起在催化剂前部粉尘颗粒集中在孔中心线，直到后部才分布均匀，因此整个孔壁磨损率减小。

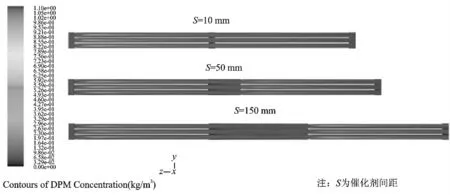
图8 催化剂孔道内的颗粒分布图Fig.8 Particle distribution in catalyst pore

2.3 孔道堵塞对催化剂磨损的影响

催化剂中间孔道堵塞与未堵塞时磨损率的对比见图9。

图9 孔道堵塞对催化剂磨损的影响Fig.9 Influence of pore blockage on catalyst erosion

由图9 可知，催化剂堵塞对端面的磨损率影响较小，堵塞与未堵塞的端面磨损率分布为3.54 ×10－4kg/(m2·s)和3.15 ×10－4kg/(m2·s)，变化不大;孔道堵塞对孔道壁面的影响较大，堵塞与未堵塞时孔壁磨损率分布为2.44 ×10－6kg/(m2·s)和4.10 ×10－6kg/(m2·s)，变化较大。对于以上现象，主要是颗粒分布和速度变化引起的。

催化剂中间孔道堵塞后颗粒浓度的分布情况，见图10。

图10 催化剂中间孔道堵塞后颗粒浓度分布Fig.10 Particle distribution in catalyst pore when pore blockage

由图10 可知，催化剂中间孔道的堵塞，对催化剂端面的颗粒分布影响较小，对孔道内颗粒运动轨迹影响较大:在催化剂外壁面的颗粒浓度明显增加，入口附近粉尘浓度达到最大，同时内壁面颗粒浓度明显减小。因此与未堵塞时的磨损相比，堵塞后的催化剂磨损部位发生明显变化，磨损主要集中在四周孔的外壁面，四周孔内壁面次之，中间孔道随着颗粒逐渐堆积磨损率减小为零，同时，由于四周孔道外壁的粉尘浓度、流速、局部冲蚀角度增加较大，引起的催化剂磨损超过了中间孔道和四周孔内壁减小程度，导致孔道整体平均磨损率增加。

3 结论

(1)催化剂孔壁磨损率随孔径的增大而减小，催化剂端面磨损率受孔径影响较小，在模拟孔径范围内，端面磨损率几乎相等。

(2)第2 层催化剂的端面磨损率随催化剂布置间距的增加而增加，当间距增加到150 mm 以后，端面磨损率几乎不变;相反，第2 层催化剂的孔壁磨损率随间距的增加而减小，当间距增加到150 mm 以后，孔壁磨损率几乎不变。

(3)当催化剂孔道堵塞时，催化剂的磨损主要集中在堵塞位置四周孔的外壁，同时磨损率较未堵塞时大。在工程实际运行中，应避免催化剂的堵塞，在条件允许时，应适当增大催化剂孔径，增强催化的抗堵和抗磨性能。

［1］ 环境保护部.关于公布全国燃煤机组脱硫脱硝设施等重点大气污染减排工程名单的公告［EB］.［2014-07-08］. http://www. zhb. gov. cn/gkml/hbb/bgg/201407/t20140711_278584.htm.

［2］ Fan Jianren，Zhou Dadong，Jin Jun，et al.Numerical simulation of tube erosion by particle impaction［J］. Wear，1991，142:171-184.

［3］ 闫洁，李文春，樊建人，等. 绕流中颗粒与柱体碰撞和磨损的直接数值模拟［J］. 浙江大学学报:工学版，2007，41(4):589-593.

［4］ Lee B E，Tu J Y，Fletcher C A J.On numerical modeling of particle-wall impaction in relation to erosion prediction:Eulerian versus Lagrangian method［J］.Wear，2002，252:179-188.

［5］ 柳成文，毛靖儒，俞茂铮.90°弯管内稀疏气固两相流及固粒对壁面磨损量的数值研究［J］. 西安交通大学学报，1999，33(9):53-56.

［6］ 张义，周文，孙志强，等. 管道内气固两相流冲刷磨损特性数值模拟［J］. 金属材料与冶金工程，2011，39(1):11-15.

［7］ 何文深，陈建军，郑佐东.SCR 蜂窝式脱硝催化剂抗磨损性能研究［J］.电力科技与环保，2011，27(5):10-12.

［8］ 肖雨亭，徐莉，贾曼，等.SCR 蜂窝式脱硝催化剂耐磨损性能模拟实验实验装置研制与应用研究［J］. 华北电力技术，2013(1):18-34.

［9］ 肖雨亭，徐莉，贾曼，等.蜂窝式脱硝催化剂在烟气中磨损行为的模拟研究［J］. 中国电力，2012，12(45):96-98.

［10］Finnie I.Erosion of surfaces by solid particles［J］.Wear，1960(3):87-103.

［11］ Bellman R，Levy A. Erosion mechanism in ductile metals［J］.Wear，1981(70):1-27.

［12］Finnie I.On the velocity dependence of the erosion of ductile metals by solid particles at low angles of incidence［J］.Wear，1978(48):181-190.

［13］Hussainova I，Kubarsepp J，Pirso J.Mechanical properties and features of erosion of cermets［J］.Wear，2001(250):818-825.

［14］Oka Y I，Mihara S，Yoshida T. Impact-angle dependence and estimation of erosion damage to ceramic materials caused by solid particle impact［J］. Wear，2009(267):129-135.

［15］ Wong C Y，Solnordal C，Swallow A，et al. Predicting the material loss around a hole due to sand erosion［J］.Wear，2012(276/277):1-15.

［16］Lester D R，Graham L A，Wu J.High precision suspension erosion modeling［J］.Wear，2010(269):449-457.