基于均匀设计的PCD刀具刃磨工艺参数研究
2015-12-23蒋朝鸿尚广云邓志平
蒋朝鸿 ,仲 良,尚广云 ,邓志平
(西华大学机械工程与自动化学院,四川成都 610039)
基于均匀设计的PCD刀具刃磨工艺参数研究
蒋朝鸿 ,仲良,尚广云 ,邓志平
(西华大学机械工程与自动化学院,四川成都 610039)
摘要本文基于均匀试验法,将PCD刀具刃磨工艺参数作为水平因素,从而在不同水平因素条件下,进行了多次的实际磨削,得到了大量的磨削数据,并对试验数据进行了回归分析,建立了回归数学模型,得到了回归方程,进而对回归方程进行F检验,验证了模型的可靠性。
关键词PCD刀具回归分析磨削
0绪论
随着难加工材料的出现,传统材料的刀具越来越难以满足现在加工的需求。近些年来,由于超硬材料聚晶金刚石(PCD)具有良好的物理性能和化学性能,因而被广泛应用于刀具的制造中,切削速度可比硬质合金提高一个数量级,同时刀具寿命也大幅度提高[1]。基于经济性考虑,目前PCD刀具的刃磨方法应用最多的是用PCD砂轮磨削PCD刀具。由于两者硬度相差不大,使得PCD刀具的刃磨相对于其它材料的刀具较难,不易获得稳定的刃磨质量[2]。前人对于PCD刀具磨除率及磨耗比的影响做了大量研究,取得了较大成果,但是缺少对刃磨质量以及刃磨工艺参数的研究。本文基于均匀设计对PCD刀具刃磨工艺参数建立了回归模型,并进行了F检验,验证了模型的可靠性[3],为PCD砂轮磨削PCD刀具的实际生产中提高刃磨质量提供借鉴和参考。
1试验设计
1.1实验设计方法
本文选择采用均匀试验设计法进行设计,一般分以下步骤:a.根据试验需要考察的目标函数确定试验指标。b.结合实际生产经验和相关专业知识选定试验因素。c.根据试验条件和经验选取试验因素的取值范围,划分试验水平。d.设计均匀设计表,排布因数和水平。e.确定试验方案,进行试验[4]。
1.2试验设计方案
试验设计方案如下:
1.2.1试验方法:均匀试验法。
1.2.2试验设备:PCD/CBN专用磨床、金刚石砂轮、PCD刀片。
1.2.3目标函数:后刀面表面粗糙度、磨削深度、刃口锯齿度、刃口圆弧半径。
1.2.4试验因素:砂轮粒度(定性)、砂轮浓度、磨削速度、磨削压强、摆动频率。
在以上的试验因素和试验指标安排下,试验应采用含定性因素混合水平试验。由于没有现成的均匀设计表可选,可使用均匀设计软件5.0版运算随机产生均匀设计表U15(15×5×5×3×3),用于安排试验。为了保证试验数据的准确性,在相同的试验参数下,对两个刀片做试验,每个刀片做两次,磨削深度为四次测量值的平均值。安排的试验表格为表1所示,相对应的试验各个因素水平划分表如表2所示。
2试验结果
在试验结果的采集过程中,磨削深度用千分尺测量,试验之前,先测量一下刀片的宽度,每试验一次,取下来再测量,两次测量之差即为磨削深度,A刀片同一组数据连续试验两次,测量两次求得平均值m,同理测出B刀片磨削深度平均值n,将m和n的平均值记入表格中。

表1 U15(15×5×5×3×3)均匀试验安排

表2 试验各因素水平划分表
测量刃口锯齿度及刃口圆弧半径,需用专用设备,本次试验采用厂家提供的从德国GFM公司进口的检测设备MikroCAD system,它能够对刀具刃口快速地进行3D测量,包括刃口锯齿度、刃口圆弧半径等。
由于PCD刀具刃磨后后刀面粗糙度的测量比较困难,此次试验PCD刀片后刀面检测所采用的设备为日本进口的SURFCOM 480A型表面粗糙度测量仪。
将被测刀片放在工作台上,调动探针的位置,最终使探针接触到被测刀片的后刀面,根据需要设置被测长度,本次检测选取4mm,测量速度亦可设置,如图1所示,点击显示屏上的开始测量按钮,即可测定该段的表面粗糙度值如图2,每个刀片测连续检测两段,取其平均值记录下来。
根据检测最终得到本次试验的数据如下页表3所示。

图1 设置测量参数
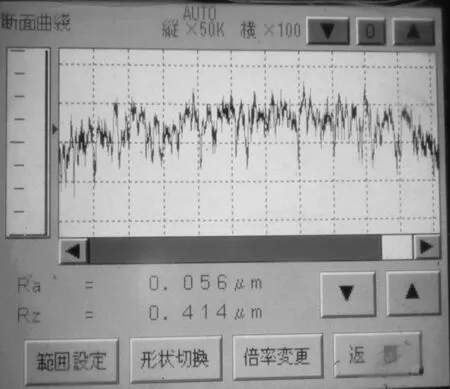
图2 被测段表面粗糙度Ra、Rz
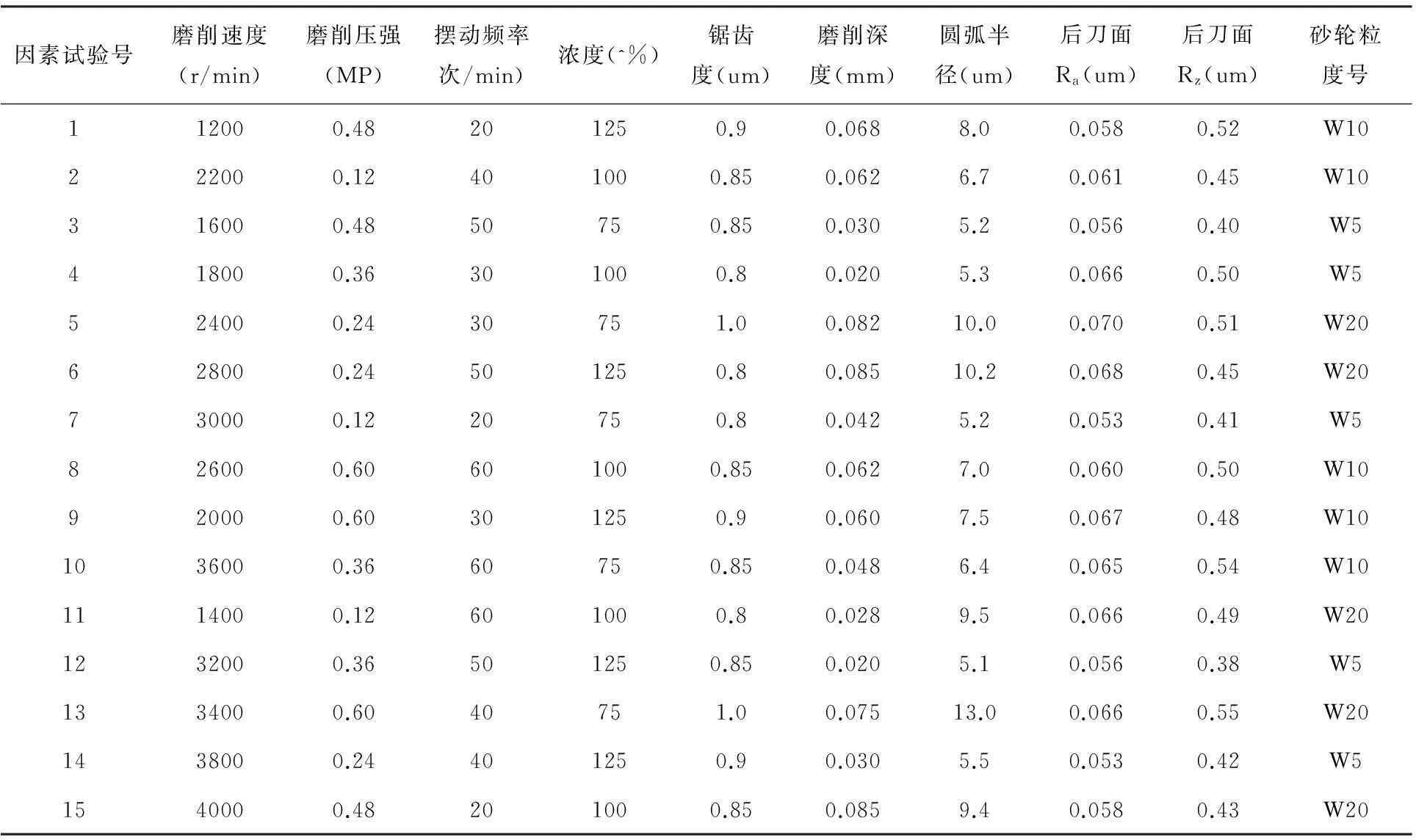
因素试验号磨削速度(r/min)磨削压强(MP)摆动频率次/min)浓度(^%)锯齿度(um)磨削深度(mm)圆弧半径(um)后刀面Ra(um)后刀面Rz(um)砂轮粒度号112000.48201250.90.0688.00.0580.52W10222000.12401000.850.0626.70.0610.45W10316000.4850750.850.0305.20.0560.40W5418000.36301000.80.0205.30.0660.50W5524000.2430751.00.08210.00.0700.51W20628000.24501250.80.08510.20.0680.45W20730000.1220750.80.0425.20.0530.41W5826000.60601000.850.0627.00.0600.50W10920000.60301250.90.0607.50.0670.48W101036000.3660750.850.0486.40.0650.54W101114000.12601000.80.0289.50.0660.49W201232000.36501250.850.0205.10.0560.38W51334000.6040751.00.07513.00.0660.55W201438000.24401250.90.0305.50.0530.42W51540000.48201000.850.0859.40.0580.43W20
3试验数据的回归分析和检验
为了建立回归方程,需将因变量和自变量参数化,定性因素A有三个状态(及水平),即A1=W5=(1,0)、A2=W10=(0,1)、A3=W20=(0,0)。这样就把定性因素A表示成三个虚拟变量。显然,这三个伪变量中只有两个是线性独立的,即A1和A2。为了方便表达,在分析过程中我们将各个因素及目标函数参数化,设:X1=磨削速度(r/min),X2=磨削压强(MP),X3=摆动频率(次/min)X4=浓度(%),Y1=锯齿度(um),Y2=磨削深度(mm),Y3=圆弧半径(um),Y4=后刀面Ra(um),Y5=后刀面Rz(um)。
使用均匀设计软件进行回归分析[5]。输入试验结果数据后,得到回归分析结果:
Y1= 0.9183807 -0.0044520 × (X4-100) -0.0555099 × A1+0.0000621 × (X1-2600)A1-1.1719349×(X2-0.36)(X2-0.36)-0.0038379×(X2-0.36)(X4-100)-0.0001298×(X3-40)(X3-40)-0.0000160×(X3-40)(X4-100)+0.0025689×(X3-40)A2+0.0000244×(X4-100)(X4-100)+0.0025375× (X4-100)A1+0.0080886×(X4-100)A2
Y2=0.0711081-0.0007586×(X3-40)-0.0538010×A1+0.0117319×A2-0.0000702× (X1-2600)(X2-0.36)-0.0000007×(X1-2600)(X3-40)-0.0000002×(X1-2600)(X4-100)-0.2505032×(X2-0.36)(X2-0.36)+0.0019250×(X2-0.36)(X3-40)-0.0031935×(X2-0.36)(X4-100) +0.0381155×(X2-0.36)A1+0.0000409×(X3-40)(X4-100)+0.0000129×(X4-100)(X4-100)
Y3=10.2096945+3.6146872×(X2-0.36)-5.2773689×A1-4.9367953×A2+0.0000580×(X1-2600)(X3-40)+27.1160919×(X2-0.36)(X2-0.36)-0.0596402×(X2-0.36)(X4-100)-3.2528083×(X2-0.36)A1-3.0608562×(X2-0.36)A2-0.0007716×(X3-40)(X4-100)+0.0161044×(X4-100)A2
Y4=0.0721521-0.0000079×(X1-2600)-0.0002987×(X3-40)+0.0001522×(X4-100)-0.0100093×A1-0.0067795×A2-0.0000002×(X1-2600)(X4-100)+0.0000020×(X1-2600)A1+0.0000145×(X1-2600)A2+0.0002039×(X2-0.36)(X3-40)+0.0072432×(X2-0.36)A2-0.0000216 × (X3-40)(X3-40)+0.0001646×(X3-40)A1+0.0003261×(X3-40)A2
Y5=0.4731518-0.0010623×(X4-100)-0.0589159×A1+0.0003856×(X1-2600)(X2-0.36)+0.0000039×(X1-2600)(X3-40)+0.0000024×(X1-2600)(X4-100)-0.0020044×(X2-0.36)(X4-100)+0.2543271×(X2-0.36)A2-0.0000914×(X3-40)(X4-100)-0.0054242×(X3-40)A1-0.0016899×(X3-40)A2+0.0000169×(X4-100)(X4-100)
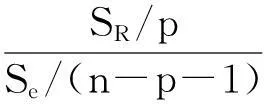
式中:SR为回归平方和;Se为残差平方和;p为SR的自由度;n-p-1为Se的自由度。
在给定的显著性水平α下,若F>F1-α(p,n-p-1),即认为回归模型可信。对于Y1(锯齿度),根据均匀设计软件分析得到其方差分析表4:

表4 Y1方差分析表
给定显著水平为0.05,可以查得F0.05(11,3)=8.763,表4中F=3400.583>>F0.05(11,3),所以,Y1的回归方程回归效果显著。根据均匀设计软件分析得出R2=0.9999,跟1很接近,表面Y1与各个自变量之间的相关性关系很密切。经计算,Y2、Y3、Y4、Y5回归方程回归效果显著,与各个自变量之间的相关性关系很密切。
4结论
根据均匀设计思想设计实验,经过多次磨削后得出了大量的实际数据;然后运用均匀设计软件对所得的数据进行分析,得到了5个独立的非线性回归方程,反映了参数与各个目标函数之间的函数关系;最后,对得到的回归方程进行了方差分析(即F检验),结果证明,所得的5个非线性回归方程具有很好的回归显著性,并且与各自变量之间的相关性很密切。
参考文献
[1] 白清顺,等.聚晶金刚石(PCD)刀具发展综述[J].工具技术,2002,36(3):7-10.
[2] 刘峰斌.聚晶金刚石刀具磨削工艺参数优化及磨削机理研究[D].大连:大连理工大学,2002.
[3] 江兆周.PCD刀具刃磨工艺及其加工有色金属的研究[D].大连:大连理工大学,2005.
[4] 李云雁. 胡传荣. 试验设计与数据处理[M]. 北京:化学工业出版社,2005.
[5] 辛涛主.回归分析与实验设计[M].北京: 北京师范大学出版社,2010.

第一作者:蒋朝鸿(1988-),男,硕士研究生,研究方向:机械制造及其自动化。
Research on PCD Tool Sharpening Process Parameters Based on Uniform Design
JIANG Chao-hong, ZHONG Liang, SHANG Guang-yun, DENG Zhi-ping
(School of Mechanical Engineering and Automation, Xihua University, Chengdu 610039)
Abstract:Bases on uniform test method and taking process parameters of PCD tool sharpening as the level factors, under the condition of different level factors, actual grinding for many times were carried on and a lot of grinding data was acquired. And those test data was analyzed with regression analysis method and the regression mathematics models were established and some regression equations were obtained. Furthermore, those regression equations were tested with F-test method and the reliability of the models was proved.
Key words:PCD cutting tool, regression analysis, grinding
文章编号:1008-5580(2015)02-048-03
中图分类号:TH16
文献标志码:A
基金项目:国家自然科学基金资助项目(NO:50775190)。
收稿日期:2014-12-05
