基于原型生成技术的手写体数字识别

任美丽，孟 亮

（太原理工大学 计算机科学与技术学院，山西 太原030024）

0 引 言

为了满足行业的需求，手写体数字的识别体系必须具有精确地识别率、可接受的分类速度和对多变字体的鲁棒性。目前，在手写体数字识别方面，有很多方法都达到了其要求的识别准确性，包括多级神经网络、支持向量机和传统的邻近算法等。然而，这些方法都没有权衡空间和时间的差异。因此，为了避免重新训练样本，浪费数字的分类时间，本文采用了基于原型技术的k－NN 邻近算法［1］进行分类识别。该技术主要包含以下几个重要的步骤：通过自适应共振理论的无监督性学习来选取能够包含所有样本特征的原型集合；利用自然演化理论的原则将原型集合进行优化，建立一个具有最小集合的边界，产生最优的最能代表整个样本的集合；通过k－NN 邻近算法将原型技术应用于MNIST 手写体数字数据库中。依据不同阶段的处理过程寻找的最优的原型集合，减少k－NN 算法的分类时间，但不影响算法分类识别的精确度，权衡手写体数字识别上的时间和空间的差异。话句话说，采用适当原型生成技术的k－NN 分类器可以权衡识别的准确率、分类速度和手写体风格多变的特征。

1 工程简介

k－NN 算法主要是针对未知的待识别的测试样本，从训练集中找出和其最接近的K 条记录，然后根据它们的主要分类来决定新数据的类别。传统的k－NN 分类器需要存储所有的训练集并依据在特征空间中最接近训练集中的样本作为所识别的类别［1］。因此，k－NN 算法中包含一个代表原型集［2］，使其在训练过程中不需要花费时间，但在识别过程中需要大量的时间，这是因为在识别阶段，k－NN 算法需要处理大量的数据。为了减少识别过程中的时间，提出了一种新的原型生成技术的方法，将其与k－NN 算法相结合。该方法集中收集主要的、最能代表原型的训练集，它具有比原训练集更小的维数，这样不仅能够提高测试样本的匹配准确度，使得测试样本在识别过程中能有效的减少训练的时间，而且还保持其具有相对较高的识别率。实验中，定义两个主要策略即原型选择和原型合成。原型选择技术主要强调的是将训练集中的样本进行压缩，从中选择出最能代表原训练集的特征集合，作为k－NN 算法的原型。原型合成技术强调主要是实现合成原型的最优化问题，以及利用原型生成技术后的k－NN 分类器的分类能力。数字图像的原型生成技术从原型选择出发进而进行原型的组合，最终形成实验所需要的原型集合，通过k－NN 算法的识别最终确定待测样本的类别。

2 基于分类的原型

通过对数字图像特征提取之后，在特征空间中，每个样本都包含一个对应的特征向量v。假设一个距离矢量d（d 是一个非负的且满足自反性条件：d（v，v）＝0），如果满足mind（v，vi）＝d（v，v′），i＝1，2，…，n，则称为v′∈｛v1，v2，…，vn｝为最近的邻居。在k－NN 规则中，对于未知向量v 的预测，需要从最近的k 个训练集中选择出最可能的类别。

假设从原训练集上选择生成一个具有代表的集合RS＝｛P1，P2，…，PM｝，表示M 个样本的原型。通过计算或是从训练集中训练得出相应的、并设计有效的距离矢量d，以及选择有效的判别特征选择出训练样本的原型，形成代表原型集合，降低训练集的维数，以便k－NN 规则利用原型技术很好的完成识别。因此，不仅要注意代表原型集合的建立，而且还需要说明特征提取和距离矢量。

2.1 特征提取

特征提取对于数字图像的识别起着关键性的作用，为了增加对待测样本的辨别能力，不仅要收集训练数字的形状的信息还要收集形状空间布局信息。形状信息的获取依据图像区域内发布的方向梯度，空间局部信息的描述依据不同图像的不同网格的多种分辨率，这样生成不同分辨率对应不同水平的特征提取方案，如图1所示。

图1 3种不同等级的特征提取方案

数字图像利用方向梯度的二进制直方图［3］进行描述，以保证其能够包含关于图像缩放、旋转、平移和对比对等变化的差异。因为图像的每一个像素点的梯度都含有相应的方向和数值大小，通过对图像中每个区域的像素点在同一方向累加的幅度值来构建相应的梯度直方图。而梯度幅值和方向的计算通过以下步骤：首先，预处理阶段的执行是生成相应的输入数字图像，包括运用Otsu算法进行的二值化处理，倾斜校正和归一化成36×36的图像。然后，根据Sobel的梯度算子在强度和方向上计算相应的梯度分量，如图2所示。最后，将每个梯度方向分解在成标准的形式［4］。

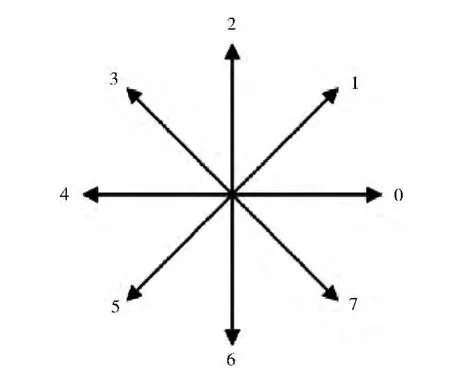
图2 每个方向的梯度分解

为了生成相应的二进制向量集，我们将所给定区域内的直方图区域的平均值作为阈值，高于阈值的部分设置为1，低于阈值的部分设置为0，例如图3所示。

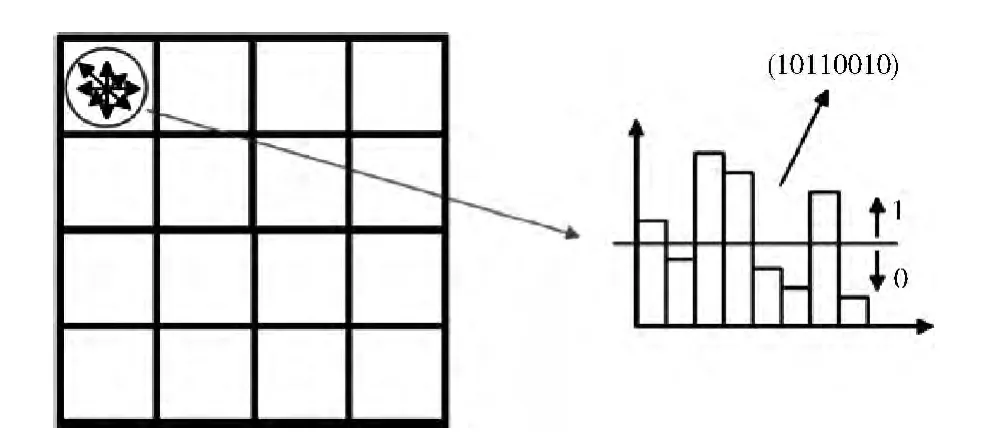
图3 方向梯度的二进制直方图

我们构建的直方图［3］采用3种不同等级的形式，6×6，4×4，2×2，为了避免局部重叠的现象，我们采用了方向梯度的二进制直方图为每一个等级提供二进制向量集。0等级 （6×6网格）由288位的向量所表示，1等级 （4×4网格）由一个128 位的向量所表示，2 等级 （2×2 网格）由一个32位的向量所表示。将这些向量链接起来构造一个具有448位向量的集合

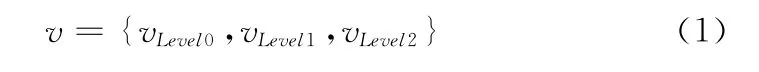
因此，特征向量v可分解成3个子向量vLevel0，vLevel1，vLevel2。

2.2 距离矢量

距离矢量在识别代表原型集RS和识别未知数字图像有着关键的作用。正是因为这个原因，在很多文献中都描述了关于提高k－NN 距离测量的方法。本文，为了提取有用的空间信息，距离矢量应该能够量化在不同等级 （如图1所示）中的梯度方向的二进制直方图的多样性，我们介绍一种距离矢量的方法——在直方图差异上的加权求和方法，设计目的是比较待测样本与训练集中的数字的、形状和结构。它依据Sokal－Michener的相异度量理论［5，6］，其定义

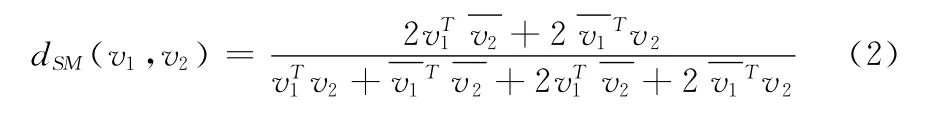
式中：v1、v2——一个具有固定长度f的向量，——内积。最终将Sokal－Michener的相异度量dSM的值被归一化到0和1之间 （0≤dSM（v1，v2）≤1）。本文所采用的测试度量［7］的定义为

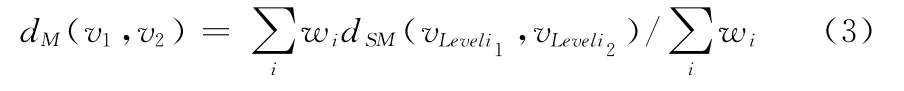
式中：v1、v2——两个比较向量

wi（i＝0，1，2）是子向量相异的权重。

3 原型选择算法——ART1

经过对图像的特征提取和距离矢量的定义之后，我们要从训练集中选择出所能代表数字类型的特征最为系统识别数字的原型，本文中，原型选择的算法采用的是自适应共振理论［8］（adaptive resonance theory，ART）。ART 的发展主要是为了避免在竞争性的网络学习中稳定性－可塑性两难的局面。稳定性－可塑性两难的局面主要解决的是既能够对新输入的数字进行学习又能够保持先前学习的信息。ART 包含了一系列不同的神经架构，其中最重要的基础架构就是ART1。它是一种无监督式学习的模型，尤其对于二进制输入模式的工作。ART1系统不仅具有相对稳定性，而且还包含一个可调节的警惕参数。另外，对于从给定的模型中选择出训练样本的代表原型方面上，ART1 的算法具有快速学习和适应不稳定环境的能力，能够从输入的数据中进行无监督式学习且能准确自动的确定数字的原型。

为了能够获得更加准确的数字原型集合，本文采用的ART1的算法的主要思想：对于每个二进制输入的向量模型v，算法都试图从以存储的数字图像原型中寻找相匹配的模型作为该数字的类别，将相似度最强的原型作为最终的数字类别。首先，引入选择函数fc用来计算二进制输入向量v 和表示原型向量的相异值。然后，通过匹配函数fm与相异值进行计算［8］，如果满足匹配条件，则先前所选的类别就是输入数据的类别，而在其学习过程依据学习函数fl不断地修改原型向量［9］以便寻找出最为相似的数字类别，但最终存储的该类别的原型不发生变化；如果条件不匹配，例如匹配条件不满足或是选择出的原型复位等。将新输入的向量v假设成为新类别的代表，将其存储在原型集中作为新的原型特征，之后，在假设测试周期结束时，算法要么找到一个存储的类别，其原型与输入的向量不完全匹配，要么创建一个新的原型。这种情况下，存储的原型集需要根据学习函数fl进行更新，并将学习的结果存储在原型集RS中。如图4所示，显示了无监督式学习过程。

图4 无监督式学习过程

作为稳定性－可塑性的结果，该算法能够通过输入模式流自动在线调节学习原型，而不是训练整个训练集。通过警惕值δ对定义原型的数据进行控制，警惕值越高，则产生较大数量的原型。显然，引入的ART1算法是一个区别定义和实现的基本框架，其中关键的要素是匹配函数fm，选择函数fc以及学习函数fl。为了实现ART1算法，我们指定测试距离矢量dM作为选择函数fc，其与匹配函数fm存在小于等于关系，与学习函数fl进行逻辑按位与运算。事实上，如果距离矢量dM在实际输入和选中原型之间存在小于等于警惕值δ，则认为匹配条件满足。

通过该算法的描述，我们需要选择一组能够具有很好代表性的原型集合作为演化策略的起点，通过代表集合的基数，自定义警惕值δ，从原训练集中选择出所能代表数字类型的原型集合RS，作为k－NN 分类器的参考。

4 原型合成

原型合成是指从给定的数据集合中选择出最优数据的原型并进行组合，形成最终所需的原型集合。在寻找代表性的数据过程中被一些学者称为NP 问题。文献中提出很多原型生成的方法和将它们应用于不同的地方。本文，我们主要是通过原型生成技术来提高k－NN 分类的效率。在识别未知样本时，我们寻找一个具有较小规模的二进制向量集合。因此，我们将原型合成看作成一个最优问题，最优的集合RS是依据相关分类的代价函数进行最小化

式中：Err（RS）——误判率。

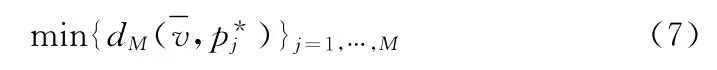
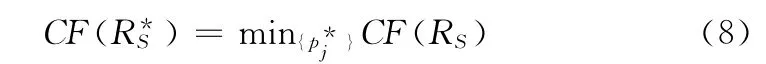
本文中，为了从原型集合RS中得到最优原型集合，我们应用演化策略 （evolution strategy）［10］在一系列的候选原型问题上。如图5所示，演化策略依据的是变异算子［11，12］。这种算子在染色体特征中引入了随机的变化因子，通常由基因突变产生的新的个体与原有的差别不是很大，换句话说，变异算子提供了一种少量的变化因子在种群融合中进行随机搜索。因此，解决最优问题就成了必要的，为了满足这些条件，我们使用了ART1基础算法描述了先前的选择。

图5 ART1－ES策略

假设初始的种群特征Pop＝｛1，2，…，NPop｝包含了所有群体NPop的特征，每个群体的特征i 是一个二进制向量，它是对代表集合的响应。中的每个元素是T 的按位向量 （其中T 是特征向量的维数）。因此，通过式 （6）可以计算出每个类别特征i 合适的值，将其作为该种群的代价函数CF（）。我们实现演化策略的过程如下：

（1）设置g ＝1和评估每个种群特征i 的值在所有的种群特征集Popg－th中的适合性。

（2）根据每个种群特征的i 值的适合程度在Popg－th对进行排列，并且根据变异率将他们分成不同的种群。

（3）生成一下代群体的过程［10］：依据每个个体所属的种群，以及相应的和进行变异，产生新的种群，之后，将产生的新的群体作为下一代种群集合Ug－th。

（4）根据目标函数计算i 的值，并为其分配合适的值，进行评估，∈Ug－th。

（5）从Ug－th选择出合适的个体srNPop，从Pop（g＋1）－th中为其分配。（sr是选择的概率）。

（6）如果停止条件满足，则终止搜索并且返回当前的种群Pop（g＋1）－th，否则，设置g ＝g＋1，继续循环步骤（2）～步骤 （6）。直到所产生个体的种群满足或者代价函数满足：，终止在种群中搜索。

5 实验结果

5.1 距离矢量的最优

表1 k－NN 识别率

为了提高识别率，应该将更多的权重应用于等级1，这是因为等级0，它具有的区域比较小可能丢失一些重要的信息，等级2，具有的区域比较大，可能包含一些没有必要的信息，而且，相异度量的线性加权组合对于提高识别率非常重要。如果我们仅仅应用等级0、等级1、等级2，则只能获得97.91%、96.87%、89.92%的识别率。这表明将这3个等级区分单独考虑，则识别率最高的为等级0，但是，等级0的识别率仍然要低于3个等级拥有相同加权组合的识别率98.77%。

5.2 原型生成技术的进化

通过大量的实验生成和比较最优原型代表集的生成。首先我们应用了ART1算法在MNIST 训练集上和根据不同的警惕函数建立不同的代表集合，通过一些测试之后，我们选择警惕参数δ ＝0.35。对于MNSIT 的测试样本，通过这个代表集最终的识别率为97.32%。

在演化策略 （ES）中，选择的参数为NPop＝10，＝100，ε＝0.01，α＝2，μr1＝0.001，μr2＝0.002，Sr＝0.5，通过测试一些数值确定k ＝3。实验运行在Matlab7.8版本上［13］，其最终的识别率最好的可达到98.73%。例外，通过演化策略生成的原型技术的识别率要比单一的依靠ART1算法生成的好，这是因为，演化策略仅仅是对ART1阶段提供的原始问题进行微调，避免使用复杂的演化算法。图6表示了每种类别的识别率和总的识别率，结果显示一些数字频繁的被误判。这是因为他们在形状上几乎是相似的，导致从代表原型集中计算距离度量过程出现无效的判决。

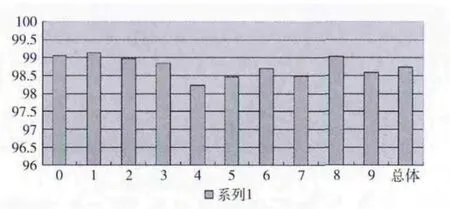
图6 每种类别的识别率和总的识别率

这种所提出的原型生成技术已经确定了721 种原型，它比MNIST 训练集的维数要小的很多，见表2。训练集具有的60000种样本，但是最终我们只需要确定其中的721种样本作为具有代表性的原型。

表2 原型集合的维数和MNIST 训练集的维数

它表明了每一个数字类别都是依靠不同的原型表示，主要的依据的是类别内部之间的不同变化，因此，需要对每个类别的不同形式进行表示是重要的。而且，传统的k－NN （k＝3）的分类算法在MNIST 上的识别率为98.85%。因此，这种技术有效的减少了分类的时间，但其识别率保持相对较高。表3 分别显示了传统k－NN 算法和原型生成技术的识别率和相应的分类时间。

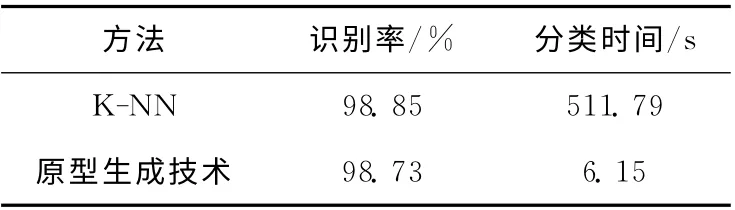
表3 传统k－NN 算法和原型生成技术的比较

6 结束语

本文提出一种采用原型生成技术的k－NN 算法来实现手写体数字的识别，该技术包含两个阶段的内容，第一阶段采用ART1理论实现决定熟悉原型和选择有效的初始解决方案，之后应用演化理论生成最终的解决方案。依据所建立的代表原型集，k－NN 分类器的识别率达到了98.73%，同时分类的时间减少。因此，该解决方案能够很好地权衡识别率和分类速度，但是，仍存在一些问题需要继续研究，例如，在演化策略中的参数的选定，本文中的参数选择主要依据的是传统数值。另外，在学习过程的更新阶段需要进一步的提升，需要选择更好的学习函数应用在ART1算法中。

［1］Angiulli F.Fast nearest neighbor condensation for large datasets classification ［J］.IEEE Transactions on Knowledge and Data Engineering，2007，19 （11）：1450－1464.

［2］Chang R，Pei Z，Zhang C.A modified editing k－nearest neighbor rule ［J］.Journal of Computers，2011，6 （7）：1493－1500.

［3］Beiping H，Wen Z.Fast human detection using motion detection and histogram of oriented gradients［J］.Journal of Computers，2011，6 （8）：1597－1604.

［4］Déniz O，Bueno G，Salido J，et al.Face recognition using histograms of oriented gradients ［J］.Pattern Recognition Letters，2011，32 （12）：1598－1603.

［5］Pekalska E，Duin RP.Beyond traditional kernels：Classification in two dissimilarity－based representation spaces［J］.IEEE Transactions on Systems，Man，and Cybernetics，PartC：Applications and Reviews，2008，38 （6）：729－744.

［6］Cunningham P.A taxonomy of similarity mechanisms for casebased reasoning ［J］.IEEE Transactions on Knowledge and Data Engineering，2009，21 （11）：1532－1543.

［7］Ciresan DC，Meier U，Gambardella LM，et al.Deep big simple neural nets excel on handwritten digit recognition ［N］.CoRR，abs／1003.0358，2010.

［8］Gil－Pita R，Yao X.Evolving edited K－nearest neighbor classifiers［J］.International Journal of Neural Systems，2008，18（6）：459－467.

［9］García S，Derrac J，Cano JR，et al.Prototype selection for nearest neighbor classification：taxonomy and empirical study［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34 （3）：417－435.

［10］Back T.Evolutionary algorithms in theory and practice：Evolution strategies，evolution programming，genetic algorithms［M］.New York：Oxford University Press，2011.

［11］Beyer H－G，Schwefel H－P.Evolution strategies：A comprehensive introduction ［J］.Journal： Natural Computing，2008，1 （1）：3－52.

［12］Danesh M，Naghibzadeh M，Totonchi MRA，et al.Data clustering based on an efficient hybrid of K－harmonic means，PSO and GA ［J］.Transactions on Computational Collective Intelligence，2011，4：125－140.

［13］QIN Xiangpei.MATLAB image processing and interface programming ［M］.Beijing：Electronics Industry Publishing，2009：454－455 （in Chinese）.［秦襄培.MATLAB图像处理与界面编程宝典 ［M］.北京：电子工业出版社，2009：454－455］.