基于能量函数的故障诊断方法与实验

周雪梅，李 辉，潘 多

（1.四川工商职业技术学院 信息工程系，四川 都江堰611830；2.四川大学 计算机学院，四川 成都610065）

0 引 言

目前，有关运动系统执行器信号分析及其故障诊断方法的研究已有很多。文献 ［3］采用H ∞和状态观测器对执行器故障进行诊断和隔离，其中用到了动力学模型、位置残差信号；文献 ［4］则基于动力学模型，采用自适应滤波的方法进行执行器故障的诊断；而Isermann在其研究工作［5］中则总结了基于模型的系统故障诊断方法。

通过分析可以发现，上述方法都是基于运动系统的动力学模型、位置等信号进行的驱动器故障诊断。算法复杂、时变性较强，而且诊断算法的物理意义不明确，不利于实际应用。在这方面，文献 ［6］采用测得的电机电流信号对刀具的断裂故障进行了诊断，具有较好的实际应用意义。而实际的运动系统中的驱动器中一般会提供用于监视用的力矩信号或者与力矩有直接关系的电机电流信号。利用此信号可以节省运算资源和传感器资源。

本文利用一般运动控制系统中冗余的力矩监视信号，研究不同类型故障诊断的方法。即利用物理意义明确的能量函数进行驱动系统故障的监视，具有方法简单、应用方便、准确可靠的优点。

1 问题描述

1.1 驱动系统故障及特点分析

从硬件构成上，包括各类数控机床、机器人等，一般数控系统可认为由控制器、驱动器、伺服电机编码器等几个关键环节构成［7］。其间的关系如图1所示。所示系统中，驱动器是弱电控制系统与强电执行机构的桥梁。即所有与电机相关的系统执行过程状态都通过驱动器反馈给控制子系统。包括电压、电流、位置等。驱动器生产商也会给控制子系统以开关或模拟信号的形式提供给用户，如：Panasoic电机驱动器、Maxon直流电机驱动器、Dynaserv直接电机驱动器等。这些驱动器具有如下特点：

（1）电流环和电压环已经集成于驱动器内部，之所以再提供这些信息，主要为一般监视控之用，往往含有大量的干扰信号；

（2）在系统运行过程中，只有超出设定的电压或电流输出才会有停机报警；而对于本文中引言部分总结出的故障，即使发生了系统也会继续运行，不会给与相应报警；

（3）驱动器中的监视功能不能分辨出是哪类故障的发生。

图1 一般数控系统构成

本文即基于驱动器中冗余的力矩监视信号对上述各类故障进行监控，为控制决策系统提供准确信息。

1.2 驱动系统故障的发生机理分析

运动系统中，执行机构的种类很多，按照与环境的关系大体可以分为两类：不与环境发生接触和与环境发生接触［8］。弧焊和焊接机器人属于无接触机器人。此类机器人在运动时，如果与惯量较小的障碍物相撞，那么由于系统都具有一定的鲁棒性，末端执行轨迹受影响较小，但此时，电机为了产生相应的转速，驱动力肯定要发生变化。一般来讲，障碍物的刚度越大、惯量越大，力矩信号变化越剧烈。而码垛机器人、数控机床、人机交互机器人等则属于后者［9］。此类机器人与环境的接触是不可避免的，如对于钻床，加工件气泡的存在，使得相同速度下，电机输出力矩会变小；刀具发生严重损伤、甚至断裂的时候，电机的输出力矩也会发生突变。

上述变化，必然引起电机驱动装置对输出电流的调整。反映到电机驱动器上，转矩监视信号 （torque monitor output）就会发生相应变化。所以说，驱动器转矩监视信号包含有与电机相关的所有信息。可以通过数据处理的方法，对此信号进行分析得到这些不同类型的系统故障。

2 基于能量函数的运动系统故障监测方法

2.1 故障诊断系统的构成

近年来，故障诊断方法的研究有了大量的研究成果，但是由于物理意义不明确、运算繁杂等原因，没能得到广泛的应用。Kaiser［10］在1990年提出了一种近似能量函数，克服了以前只用幅值或频率来描述信号能量大小的片面性，而且有利于检测信号能量的变化特性，并得到了大量的研究和应用，在文献 ［11］中，该思想得到了进一步的完善。

对于一般数控系统，由于其力矩监视信号可以被直接获得，根据上述思路，可构建故障诊断系统如图2 所示。图中，A/D 转换为高速数据采集，信号分析可以采用多种方法，本文中采用具有清晰物理意义的新颖能量函数，对故障归类得到C1，C2，…Cn，并从n 类故障中确定某一种故障的发生。

图2 基于力矩信息的故障诊断系统的构成

但是，上述应用方法中，一般需要额外的传感器进行信号的采集，加大了系统的复杂性。本文基于上述分析，利用驱动器中冗余的力矩监视信息对系统的运行状况进行监控。

2.2 基于能量函数进行故障诊断

文献 ［10］利用牛顿定律得到表征某信号能量的结论：

如果信号的采样频率是其最高频率的八倍以上，那么对信号能量的测量可以表示为

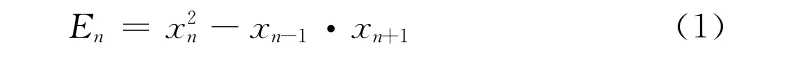
式中：xn——对信号在n时刻的采样，En——算法的输出，即能量的表征量。

由式（1）可知：一方面，此算法具有对称性，对采样点求反，不会影响结果；另一方面，因为没有除运算，此法允许信号过零；除此之外，算法的简单性大大方便了使用。

对于驱动系统信号，利用能量算子进行能量运算的方法表示如下

式中：n——采样点。

由于能量函数E［T（n）］＜0或E［T（n）］＞0都可能存在，所以在故障阈值L 下，故障未发生的条件为

多步平滑非线性能量算子 （SPNEO）

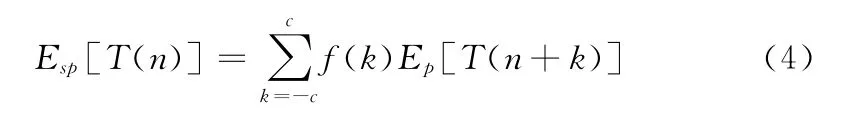
上式中，系数项

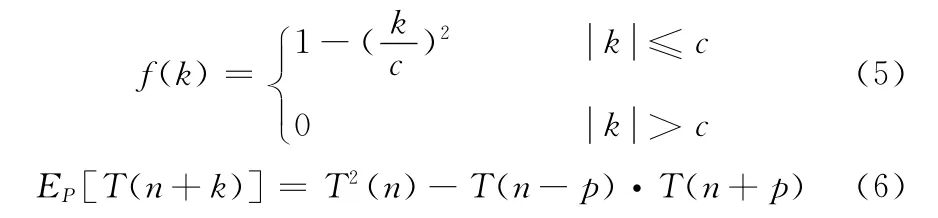
其中，p 为延迟的步数。

式（2）和式 （4）可以认为是低通滤波器，通过对c和p 的选择可以实现对不同频段信号的滤波。

2.3 应用过程的关键点

方法应用过程中的关键点可以概括如下几点：

（1）信号的采样频率应该足够高，大于信号频率的八倍；

（2）选择合适的c 和p 的值，用于诊断不同类型的故障；

（3）选择合适的阈值，作为准确判断故障的发生的准则。

2.4 故障发生的诊断步骤

根据上述分析，可以得到利用非线性能量函数进行故障监视与诊断的步骤如图3所示。

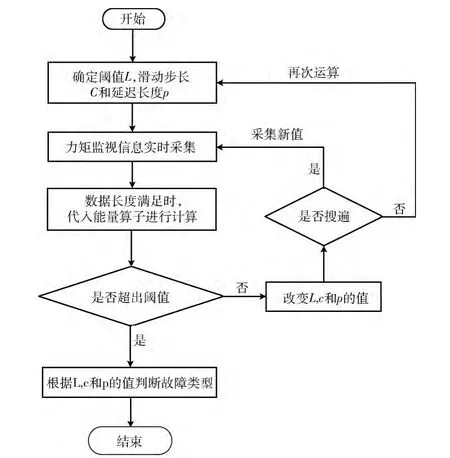
图3 故障诊断流程

在图3中，改变L，c和p 的值是为了使得能量函数具有对各频段的分析能力，这也是一个扫描故障类型的过程；当完成一次扫描后，就可以采集新数据，进行下一个循环的运算。

3 仿真验证与应用

本文采用了软件仿真与实际应用两种思路，验证上述方法有效性，并在应用的过程中给出应用此种方法的关键点。

3.1 软件仿真实验

本研究中的软件仿真在Matlab7.1 环境中进行，信号的生成过程采用Simulink框图形式，信号分析在环境m 函数中进行。

模拟转矩信号的基本信号为

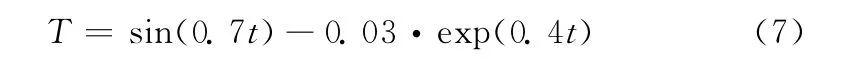
在此信号上叠加方差为0.0001，均值为0的白噪声信号作为干扰。为了模拟故障的发生，在5s时刻，叠加幅值为0.2单位，宽度为0.05s的突变故障脉冲信号。

在采样周期为5 ms时得到模拟转矩时间序列T（n），设其长度为N。最终产生的信号曲线如图4所示。

图4 模拟故障信号

在能量算子式 （2）中，由于需要一步向前和向后的信号，所以会使得信号的长度缩短。由于采样时间较短，这一方可以用零能量来替换，另外也可以将初始点和结尾点舍去，本研究中采用了舍去的处理方法。

根据上文算法，在Matlab7.1中编写m 函数，运算得到能量序列E ［T（n）］，长度为N－2。通过与阈值L 的比较，可以诊断出5s时刻突变故障的发生。将能量序列绘制如图5所示。

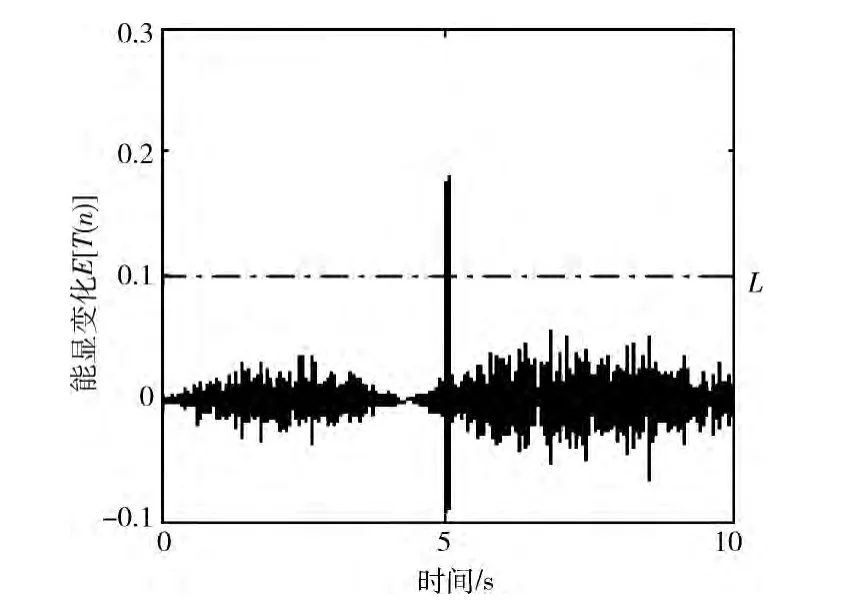
图5 基于NEO 的能量函数

仿真结果表明，一步能量算子能以给定阈值为参考，有效诊断突变故障的发生。

3.2 应用实验

以X－Y－Z数控运动平台在运动过程中撞击质量为25kg的静止刚体 （钢板）过程为研究对象，在系统运动过程中采集驱动器冗余力矩监视信号，并进行分析。图6是平台实物照片。

图6 X－Y－Z平台实验装置

力矩信号由此运动控制系统中松下交流伺服电机驱动器中的力矩监视信号 （torque monitor output）采集得到，采样周期为0.002s。此信号在一般的运动控制系统中只作为力矩监视之用，甚至闲置。实时的信号采集与运算所采用的软硬件环境分别为加拿大Quanser公司的Wincon软件和多功能Q8运动控制板卡。

通过对撞击刚体情况下与无撞击情况下力矩监视电压信号的采集与记录，进行绘制后得到图7，图中实线为存在外部撞击时的力矩信号。对式 （2）的应用结果为图8，当式（6）中p＝1，则得图9，经过式 （4）得到多步平滑能量函数值构成的能量序列Esp［T（n）］将其绘制得到曲线如图10所示，此时，c＝70，p＝50。

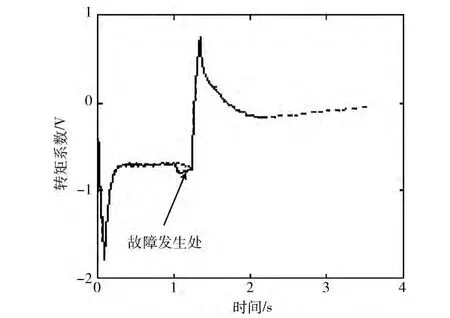
图7 力矩曲线

由图8～图10可以清晰准确判断出故障发生的状态以及时刻。

同时，通过上述对两种不同能量函数的应用可以总结为以下几点：

（1）对于突变故障的发生，由于带来信号能量的突变，可以通过一步能量函数队故障的发生进行准确的诊断，同时运算量也最小；

图8 一步能量算子运算结果

图9 仅平滑算子结果

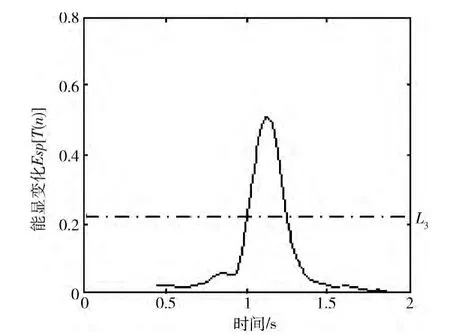
图10 SPNEO 运算结果

（2）对于变化较缓慢的故障，由于能量的变化较慢，适于采用多步滑动能量算子进行故障的探测，运算量随着信号变化的趋缓而增大；

（3）居于两者之间的故障信号变化，可以采用单步滑动能量算子进行探测；

（4）采用两种不同的能量函数进行运算时，采用的能量函数阈值是不同的，且遵循的原则是：窗口越大，滞后时间越长，阈值也越大。

4 结束语

本文提出了基于能量函数进行故障诊断与类型分类的方法。给出了基于能量函数的故障诊断原理，分析了应用过程中的关键点，并提供了详细的诊断过程流程图。通过基于Matlab的软件仿真以及以数控运动平台为对象的诊断进行了实验，实验结果表明了该方法的有效性。同时，对不同能量函数及其参数的选择进行了详细的分析，给出了进行故障诊断的指导性原则。本文中提出的方法对于数控机床、多自由度机器人系统、人机交互系统具有很好的利用价值。

［1］Ollero A，Boverie S，Goodall R，et al.Mechatronics，robotics and components for automation and control－IFAC milestone report ［J］.Annual Reviews in Control，2012，30 （1）：41－54.

［2］Torgny Brogardh.Present and future robot control development－an industrial perspective ［J］.Annual Reviews in Control，2011，31 （1）：69－79.

［3］De Luca A，Mattone R.An identification scheme for robot actuator faults［J］.IEEE/RSJ International Conference on Intelligent Robots and Systems，2013，8 （6）：1127－1131.

［4］Alessandro De Luca，Raffaella Mattone.An adapt－and－detect actuator FDI scheme for robot manipulators［J］.IEEE International Conference on Robotics ＆ Automation，2011，4 （2）：4975－4980.

［5］Rolf Isermann.Model－based fault－detection and diagnosis－sta－tus and applications ［J］.Annual Reviews in Control，2012，29 （1）：71－85.

［6］Li Xiaoli，Du R，Berend Denkena，et al.Tool breakage monitoring using motor current signals for machine tools with linear motors ［J］.IEEE Transactions on Industrial Electronics，2010，52 （5）：1403－1408.

［7］HU Yabo，WU Yawen.Situation and development of CNC lathes［J］.Machine ＆ Hydraulics，2011，7 （5）：4－6 （in Chinese）. ［胡亚波，吴亚文.我国数控车床的现状与发展［J］.机床与液压，2011，7 （5）：4－6.］

［8］DU Kunmei，LI Tiecai.Flywheel torque servo motor control system ［J］.Electric Machines and Control，2011，5 （2）：119－120（in Chinese）.［杜坤梅，李铁才.惯性飞轮电机力矩伺服控制系统［J］.电机与控制学报，2011，5 （2）：119－120.］

［9］Lames F Kaiser.On a simple algorithm to calculate the‘energy’of a signal［J］.International Conference on Acoustics，Speech and Signal Processing，2010，11 （1）：381－384.

［10］Petros Maragos，James F Kaiser，Thomas F Quatieri.On amplitude and frequency demodulation using energy operators［J］.IEEE Transactions on Signal Processing，2013，41（4）：1532－1550.

［11］WANG Aiping.Model reference adaptive methods in non－linear actuator fault diagnosis ［J］.Control and Decision，2011，16 （4）：587－590 （in Chinese）. ［王爱平.参考模型自适应方法在非线性执行器故障诊断中的应用 ［J］.控制与决策，2011，16 （4）：587－590.］