基于信息熵的粗糙K－prototypes聚类算法

欧阳浩，戴喜生，王智文，王 萌

（1.广西科技大学 计算机学院，广西 柳州545006；2.广西科技大学 电气与信息工程学院，广西 柳州545006）

0 引 言

现实世界中存在的数据对象，通常既具有数值属性也具有分类属性。但大多现有的聚类［1－5］算法只能分析数值属性或者分类属性［6－7］，当它们在分析混合属性的数据对象时，首先需要完成数据类型的转化。针对这一问题，Huang提出了K－prototypes算法，该算法是将可分析数值属性的K－means算法与可分析分类属性的K－mode算法相结合而设计的算法［6］。K－prototypes算法可以分析混合属性，但具有一定缺陷：①对初始均值点的选择敏感；②容易受到噪声干扰；③样本间的差异度计算对于分类属性不明显［7－10］；④不能分析模糊以及不确定性问题等［11－13］。针对问题①－③，文献 ［7］提出了二次聚类的方式，并且对于数值属性的差异度计算采用比值方式将其映射为区间（0，1］之间的值，但此方法需重复聚类计算分析；文献 ［8］计算新插入样本的分类属性值，以在整个簇中此属性值出现的频率来判断二者之间的距离；文献 ［9，10］通过计算簇中样本与均值点数值属性的差值之和的倒数，来确定每个数值属性的权值。针对问题④，文献 ［11－13］对于K－prototypes算法引入了模糊理论的概念，使其具有一定的解决模糊性和不确定性问题的能力；文献 ［14］采用层次聚类的方式实现混合属性的聚类分析；文献 ［15］采用自组织神经网络的方式完成聚类分析。以上各文献的方法均无法确定每个分类属性对于聚类结果的影响，恰恰在现实生活中，每个分类属性对于分类或聚类的结果的影响程度是不同的［16］。而且，这些算法缺乏在知识不完备的情况下对于不确定性问题的分析能力。

本文首先引入信息熵理论，聚类分析中，通过计算各分类属性的信息增益，确定此属性的权值大小。然后，通过粗糙的分析方式［17］，使得此算法在数据存在噪声、不够精确、不够完整的情况下，也能做出较好的分析。实验结果表明，本文提出的基于信息熵的粗糙K－prototypes 聚类算法 （entropy rough K－prototypes，ER－K－prototypes）有效。

1 K－prototypes算法

K－prototypes算法是将K－means算法与K－mode相结合而设计的一种新的算法，此算法可以处理混合属性的数据集［3］。令U ＝｛x1，x2，…，xn｝表示由n个样本构成的集合。其中，xi＝｛xi1，xi2，…，xip，xi（p＋1），…，xm｝表示第i个样本，其具有m 个属性，其中前p个属性为数值属性，而p＋1至m 个属性为分类属性。与K－prototypes算法相关的定义如下描述。

定义1 样本间数值属性距离。本文数值属性的距离采用欧氏距离，给定任一两个样本xi和xj，其数值属性的距离d1定义为

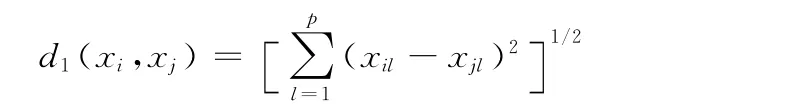
定义2 样本间分类属性距离。给定任一两个样本xi和xj，其分类属性的距离d2定义为

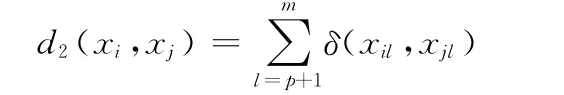
其中

定义3 样本间相异度。给定任一两个样本xi和xj，样本间的相异度为数值属性距离d1和分类属性距离d2之和，其定义为

其中，γ为分类属性的权重。

定义4 模。令vi表示为类Ci的模，其中类Ci由h 个样本对象构成，即Ci＝｛x1，x2，…，xh｝。则，模vi的数值属性取类Ci中各个样本的数据属性的平均值，而分类属性取类Ci中各个分类属性中出现频率最高的值。

定义5 平均误差函数。设p为样本对象，vi为类Ci的模，则聚类的平均误差函数定义为

K－prototypes算法的算法描述如下：

输入：n 个样本对象；类的数目k；分类属性的权重γ；停止阈值ε。

输出：聚类结果。

步骤如下：

（1）随机选择k个样本作为初始类的模；

（2）按照定义3的公式计算各个样本对象与各个模之间的距离，并且将此样本对象划分到与之距离最近的模所代表的类中；

（3）对于每个类按照定义4重新计算出类的模。

按照定义5计算出聚类的平均误差E。Epre表示上一次计算的平均误差，当｜E－Epre｜＜ε时停止算法。否则，跳转到步骤 （2）。

2 基于信息熵的分类属性相异度

K－prototypes算法在计算分类属性时，并未区分各个分类属性对于聚类结果的影响程度。在现实生活中，不同的分类属性对于聚类结果的影响程度是不同的，如在分析客户信息时，其中电话号码，姓名等分类属性，它们并不能有助于聚类的计算。经典的决策树ID3算法中，在分类过程中，引入了信息熵的相关概念［13］。本文也将使用信息熵的概念来确定各个分类属性的重要程度，并且根据其重要性重新定义样本间的相异度。基于信息熵的分类属性相异度相关的定义如下。

定义6 信息熵。设S是n 个数据样本的集合，将样本集划分为c个不同的类Ci（i＝1，2，…，c），每个类Ci含有的样本数目为ni，则S 划分为c 个类的信息熵为

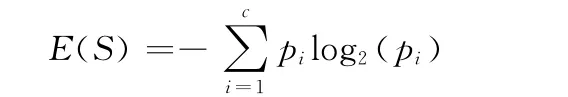
其中，pi为S 中的样本属于第i类Ci的概率，即pi＝ni/n。

定义7 期望熵。假设属性A 的所有不同值的集合为Value（A），Sv是属性A 的值为v 的样本子集，即Sv＝｛s∈S｜A（s）＝v｝。属性A 对样本集Sv分类的熵为E（Sv），而属性A 的期望熵为

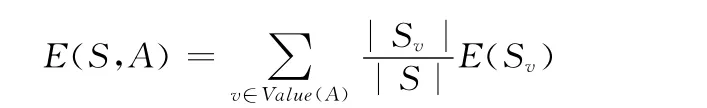
定义8 信息增益。属性A 相对样本集合S 的信息增益Gain（S，A）定义为

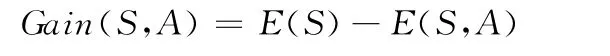
基于信息熵的分类属性相异度计算，对于经典的Kprototypes算法中分类属性距离的计算做了相应的调整，其变化如定义9所示。样本间相异度的调整见定义10。

定义9 基于信息熵的样本间分类属性距离。给定任一两个样本xi和xj，它们的分类属性包括Al（l＝p＋1，…，m），则基于信息熵的样本间分类属性距离dEntropy2定义为

定义10 基于信息熵的样本间相异度。给定任一两个样本xi和xj，样本间的相异度为数值属性距离d1和基于信息熵的分类属性距离dEntropy2之和，其定义为

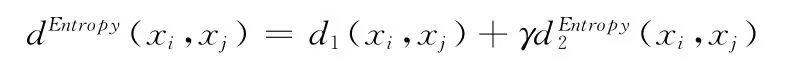
其中，γ为分类属性的权值。

3 ER－K－prototypes算法

3.1 ER－K－prototypes的粗糙性

经典的K－prototypes聚类算法对于孤立点敏感，且初始类中心的选取将影响聚类结果。为解决这些问题。模糊K－prototypes从集合的含混性的角度来完成混合型数据的聚类分析。本文将从知识表达的不精确性［2］的角度，将粗糙集的概念引入K－prototypes聚类算法中。

文献 ［18］中提出了基于粗糙集理论的聚类算法需要遵循的三条原则：

（1）一个样本只能属于一个类的下近似。

（2）若样本属于某个类的下近似，那么它也属于这个类的上近似。

（3）若样本不属于任何类的下近似，那么它属于两个或两个以上类的上近似。

定义11 粗糙模。U ＝｛x1，x2，…，xn｝表示由n个样本构成的集合。其中，xj＝｛xj1，xj2，…，xjp，xj（p＋1），…，xm｝表示第j个样本，其具有m 个属性，其中前p 个属性为数值属性，而p＋1至m 个属性为分类属性。引入粗糙集理论后，用表示类Ci的上近似，C－i表示类Ci的下近似，表示Ci的边界，并且＝－。类Ci的粗糙模vi的数值属性的计算公式如下

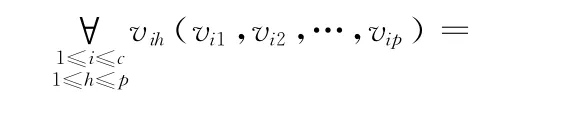
以上计算中，c表示模的数目；wl，wbn则分别表示模的下近似和边界的权值，而且在分析中wbn表示了模的粗糙性，一般则表示类Ci的下近似和边界中样本的数量。

而对于vi的分类属性，则取各个分类属性中出现频率最高的值

基于信息熵的粗糙K－prototypes聚类算法将计算各样本xj与各个粗糙模v 的距离，其中（xj，vi）表示最小距离，（xj，vk）表示次小距离，当二者的差值小于一定粗糙距离阈值η时，即｜（xj，vi）－（xj，vk）｜＜η，则认为该样本属于这两个模的上近似，否则将此样本划分到最近模的下近似中，从而完成聚类分析。

3.2 ER－K－prototypes算法描述

根据以上的理论描述，以下给出基于信息熵粗糙Kprototypes的算法描述。

输入：n 个样本对象；类的数目k；分类属性的权值γ；下近似权值wl，边界权值wbn；粗糙距离阈值η；停止阈值ε。

输出：聚类结果。

步骤如下：

（1）随机选择k个样本作为初始的类的粗糙模；

（2）按照定义10的公式计算任意样本对象xj与各个粗糙模v之间的距离；

（4）对于每个类，按照定义11 重新计算出类的粗糙模；

（5）按照定义5计算出聚类的平均误差E，此处的模为步骤 （3）计算所得的粗糙模。Epre表示上一次计算的平均误差，当｜E－Epre｜＜ε时停止算法。否则，跳转到步骤 （2）。

4 算法验证

4.1 正确率评价函数

为比较各算法分析中的正确率，本文引用文献 ［4］中的聚类正确率的定义，其描述如下。

定义12 聚类正确率。聚类算法f 将样本集合U ，划分为k个类，用corr＿ci表示第i个类中被正确聚类样本的个数，｜U ｜表示集合中样本个数。则聚类的正确率ac＿rate（D/f）为

4.2 实验验证

本文采用Visual C＋＋编写实验程序分析算法的有效性，运行环境为：Intel（R）Core（Tm）2Duo CPU ET500＠2.93GHz 2.93GHz，2.0GB内存，Window 7系统。实验数据为UCI机器学习库［19］中的Heart Disease （简称Heart），Acute Inflammations （简称Acute），Credit Approval（简称Credit），Zoo这4个混合型数据集。数据集描述见表1。

表1 数据集描述

与本文提出的ER－K－prototypes相比较的算法为同样对混合型数据具有分析能力的K－prototypes算法以及Fuzzy－K－prototypes算法。在分析前，需要对各数据集进行归一化处理，以消除各数据属性因为取值范围的不同而带来的干扰。分类属性的权值γ取值为：分类属性数/数值属性数；下近似权值wl＝0.9；边界权值wbn＝0.1；粗糙距离阈值η取值为：属性总数×0.1；停止阈值ε 取值为：0.001；样本数n与类别数目k 根据表1中的实际情况设定。其它参数以及最终的聚类的正确率见表2。

表2 部分参数及聚类正确率比较

从表2可以看出，ER－K－prototypes正确率明显优于Kprototypes和Fuzzy－K－prototypes，从而验证此算法是有效的。从定性上分析，其有效性来自于两个方面。

一方面，ER－K－prototypes在计算分类属性距离时，通过计算各个分类属性的信息熵来确定其在计算过程中的权值，从而确保对于有效的聚类起关键影响的属性，其权值更大，从而有利于聚类分析逐渐趋于正确。此更符合现实中事物的属性特征。

另一方面，ER－K－prototypes引入了粗糙集的概念，从而具备一定的处理非确定性问题的能力。在背景知识不确定、不完整，或者存在噪声时，不需要引入先验知识的前提下，也能做出比较正确的分析。

5 结束语

传统的K－prototypes，在对混合型数据进行聚类分析时，将属性分为两大类：数值属性和分类属性。在聚类计算时，并未考虑各个属性对于聚类结果的影响程度。Fuzzy－K－prototypes虽然引入了模糊性的概念，但对分类属性的分析同样存在此问题。本文提出的ER－K－prototypes引入了信息熵的概念，分析时需确定各分类属性的信息增益，此更符合现实中的分类问题。同时，ER－K－prototypes引入的粗糙集概念，能处理非确定性问题，可以在一定程度上避免噪声的干扰。实验验证此方法更有效。

ER－K－prototypes对于数值属性的分析还不完善，需要今后做进一步的研究。同时在以后的研究中，需要将粗糙理论与模糊理论相结合，应用于混合数据的聚类分析中。

［1］Han Jiawei，Micheline Kamber，Pei Jian.Data mining：Concept and techniques ［M］.3rd Edition.Beijing：China Machine Press，2012.

［2］Saeed Aghabozorgi，Ying Wah Teh.Stock market co－movement assessment using a three－phase clustering method ［J］.Expert Systems with Applications，2014，41 （4）：1301－1314.

［3］Donatella Vicari，Marco Alfó.Model based clustering of customer choice data［J］.Computational Statistics ＆Data Analysis，2014，71：3－13.

［4］Dhiah Al－Shammary，Ibrahim Khalil，Zahir Tari，et al.Fractal self－similarity measurements based clustering technique for SOAP Web messages ［J］.Journal of Parallel and Distributed Computing，2013，73 （5）：664－676.

［5］Michael Hackenberg，Antonio Rueda，Pedro Carpena，et al.Clustering of DNA words and biological function：A proof of principle ［J］.Journal of Theoretical Biology，2012，297（21）：127－136.

［6］Huang Z.Clustering large data sets with mixed numeric and categorical values ［C］//Proceedings of the First Pacific Asia Knowledge Discovery and Data Mining Confenence，Singapore：World Scintific，1997：21－34.

［7］SUN Haojun，SHAN Guanghui，GAO Yulong，et al.Algo－rithm for clustering of high－dimensional data mixed with numeric and categorical attributes ［OL］. ［2013－11－14］.http：//d.g.wanfangdata.com.cn/Periodical ＿pre ＿849c8593－e9c8－4664－aa16－c3e122d74bc8.aspx （in Chinese）. ［孙 浩军，闪光辉，高玉龙，等.一种高维混合属性数据聚类算法 ［OL］.［2013－11－14］.http：//d.g.wanfangdata.com.cn/Periodical＿pre＿849c8593－e9c8－4664－aa16－c3e122d74bc8.aspx.］

［8］CHEN Wei，WANG Lei，JIANG Ziyun.K－prototypes based clustering algorithm for data mixed with numeric and categorical values ［J］.Journal of Computer Applications，2010，30 （8）：2003－2005 （in Chinese）. ［陈韡，王雷，蒋子云.基于K－prototypes的混合属性数据聚类算法 ［J］.计算机应用，2010，30 （8）：2003－2005.］

［9］Ji Jinchao，Bai Tian，Zhou Chunguang，et al.An improved K－prototypes clustering algorithm for mixed numeric and categorical data［J］.Neurocomputing，2013，120：590－596.

［10］Huang ZX，Ng MK，Rong HQ，et al.Automated variable weighting in k－means type clustering ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27 （5）：657－668.

［11］CHEN Ning，CHEN An，ZHOU Longxiang.Fuzzy K－prototypes algorithm for clustering mixed numeric and categorical valued data［J］.Journal of Software，2001，12 （8）：1107－1119 （in Chinese）.［陈宁，陈安，周龙骧.数值型和分类型混合数据的模糊K－prototypes 聚类算法 ［J］.软件学报，2001，12 （8）：1107－1119.］

［12］ZHOU Caiying，HUANG Longjun.Improvement of the method to choosing the initial value of fuzzy K－prototype clustering algorithm ［J］.Computer Science，2010，37 （7A）：69－70 （in Chinese）.［周才英，黄龙军.模糊K－prototype聚类算法初始点选取方法的改进 ［J］.计算机科学，2010，37（7A）：69－70.］

［13］Ji Jinchao，Pang Wei，Zhou Chunguang，et al.A fuzzy Kprototype clustering algorithm for mixed numeric and categorical data［J］.Knowledge－Based Systems，2012，30：129－135.

［14］Chung－Chian Hsu，Chen Chinlong，Su Yuwei.Hierarchical clustering of mixed data based on distance hierarchy ［J］.Information Sciences，2007，177 （20）：4474－4492.

［15］Tai Weishen，Chung－Chian Hsu.Growing self－organizing map with cross insert for mixed－type data clustering ［J］.Applied Soft Computing，2012，12 （9）：2856－2866.

［16］Quinlan JR.Induction of decision tree ［J］.Machine Learning，1986 （1）：81－106.

［17］HU Qinghua，YU Daren.Application rough computation［M］.Beijing：Science Press，2012 （in Chinese）. ［胡清华，于达仁.应用粗糙计算 ［M］.北京：科学出版社，2012.］

［18］GUO Jinhua，MIAO Duoqian，ZHOU Jie.Shadowed sets based threshold selection in rough clustering ［J］.Computer Science，2011，38 （10）：209－210 （in Chinese）. ［郭晋华，苗夺谦，周杰.基于阴影集的粗糙聚类阈值选择 ［J］.计算机科学，2011，38 （10）：209－210.］

［19］UCI database ［EB/OL］.http：//archive.ics.uci.edu/ml/datasets.html，2013.