CART决策树的两种改进及应用

张 亮，宁 芊

（四川大学 电子信息学院，四川 成都610065）

0 引 言

在决策树算法中，分类与回归树CART-（classification and regression trees）算法是一种十分有效的非参数分类和回归方法［1］。CART 选择具有最小GINI系数值的属性作为分裂属性［2］，并按照节点的分裂属性，采用二元递归分割的方式把每个内部节点分割成两个子节点，递归形成一棵结构简洁的二叉树。但CART 算法存在以下不足：一方面，选取内部节点的分裂属性时，对于连续型描述属性，CART 算法将计算该属性的每个分割点的GINI系数，再选择具有最小GINI系数的分割点作为该属性的分割阈值，如果属性集中连续属性个数很多且连续属性的不同取值也很多，采用这种方式建立的决策树计算量会很大；另一方面，决策树在选择叶节点的类别标号时，以-“多数表决”的方式选择叶节点中样本数占最多的类别标识叶节点［3］，虽然在多数情况下，“多数表决”是一个不错的选择，但这会屏蔽小类属数据对分类结果的表决。针对CART 算法这两方面的不足，本文将Fayyad边界点判定原理［4］应用于CART算法，并基于关键度度量［5］选择叶节点的类别标号，有效减少了处理连续型描述属性的计算量，提高了决策树的生成效率，在样本集主类类属分布不均，小类属样本并不是稀有样本的情况下，使小类属样本得到了表达，提高了决策树的分类准确率。

1 CART算法原理

CART 算法采用最小GINI系数选择内部节点的分裂属性［6］。根据类别属性的取值是离散值还是连续值，CART算法生成的决策树可以相应地分为分类树和回归树［7］。本文将CART 算法用于分类问题的研究，因此采用的是分类树，形成分类树的步骤如下：

步骤1 计算属性集中各属性的GINI系数，选取GINI系数最小的属性作为根节点的分裂属性。对连续属性，需计算其分割阈值，按分割阈值将其离散化，并计算其GINI系数；对离散属性，需将样本集按照该离散属性取值的可能子集进行划分 （全集和空集除外），如该离散属性有n 个取值，则其有效子集有2n－2个，然后选择GINI系数最小的子集作为该离散型属性的划分方式，该最小GINI系数作为该离散属性的GINI系数。

GINI系数度量样本划分或训练样本集的不纯度，不纯度越小表明样本的 “纯净度”越高［8］。

GINI系数的计算：

（1）假设整个样本集为S，类别集为 ｛C1，C2，…，Cn｝，总共分为n类，每个类对应一个样本子集Si（1≤i≤n）。令｜S｜为样本集S 的样本数，｜Ci｜为样本集S 中属于类Ci的样本数，则样本集的GINI系数定义如下

其中，pi＝｜Ci｜／｜S｜为样本集中样本属于类Ci的概率。

（2）在只有二元分裂的时候，对于训练样本集S 中的属性A 将S 分成的子集S1和S2，则给定划分S 的GINI系数如下公式

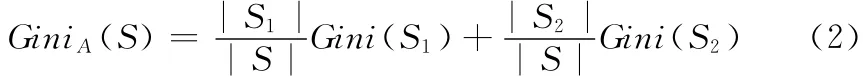
其中，｜SK｜／｜S｜为第k （k＝1，2）个子集占整个样本集的权值，为在属性A 上划分样本集S 的GINI系数。

步骤2 若分裂属性是连续属性，样本集按照在该属性上的取值，分成＜＝T 和＞T 的两部分，T 为该连续属性的分割阈值；若分裂属性是离散属性，样本集按照在该属性上的取值是否包含在该离散属性具有最小GINI系数的真子集中，分成两部分。

步骤3 对根节点的分裂属性对应的两个样本子集S1和S2，采用与步骤1相同的方法递归地建立树的子节点。如此循环下去，直至所有子节点中的样本属于同一类别或没有可以选作分裂属性的属性为止。

步骤4 对生成的决策树进行剪枝。

对于某个连续型属性Ac，假设在某个节点上的样本集S的样本数量为total，CART算法将对该连续属性作如下处理：

（1）将该节点上的所有样本按照连续型描述属性Ac的具体数值，由小到大进行排序，得到属性值序列 ｛A1c，A2c，…，Atotalc｝。

（2）在取值序列中生成total－1个分割点。第i（0＜i＜total）个分割点的取值设置为Vi＝ （Aic＋A（i＋1）c）／2，它可以将节点上的样本集划分为S1＝ ｛s｜s∈S，Ac（S）≤Vi｝和S2＝ ｛s｜s∈S，Ac（S）＞Vi｝两个子集，Ac（S）为样本s在属性Ac上的取值。

（3）计算total－1 个分割点的GINI系数，选择GINI系数最小的分割点来划分样本集。

2 CART算法选取连续属性分割阈值的改进

在上述对连续型描述属性的离散化过程中，CART 算法要计算每个分割点的GINI系数，而每个连续型描述属性的分割点为节点的样本数目减1。若样本集的样本数很多、连续型描述属性很多、且决策树的节点数也很多时，如在本文的故障诊断项目中，待分类样本数在5000以上，属性个数在60以上。随着样本维数的增高，算法的计算量也随之增大，构建决策树的效率就会降低。文献 ［4，9］将“Fayyad边界点判定原理”用于改进C4.5算法的连续型描述属性的分割阈值的选择，由于熵和GINI系数相似，都刻画了样本集的纯净度：熵和GINI系数越小，样本集越纯净。因此本文将其用于CART 算法，对CART 算法中选择连续型描述属性的分割阈值的计算复杂性问题提出了一些改进。

2.1 Fayyad边界点判定原理

定义1 边界点［9］：属性A 中的一个值T 是一个边界点，当且仅当在按属性A 的值升序排列的样本集中，存在两个样本s1，s2∈S具有不同的类，使得A（s1）＜T＜A（s2），且不存在任何的样本s∈S，使A（s1）＜A（s）＜A（s2）。S为样本集，A（s）表示样本s的属性A 的取值。

定理1 Fayyad边界点判定定理［9］：若T 使得E（A，T；S）最小，则T 是一个边界点。其中，A 为属性，S 为样本集，E 为在属性A 上划分样本集S的平均信息量，也称平均类熵，T 为属性A 的阈值点。该定理表明，对连续属性A，使得样本集合的平均类熵达到最小值的T，总是处于排序后的样本序列中两个相邻异类样本之间，也即使得样本集合的平均类熵达到最小值的T 是属性A 的一个分界点。

2.2 熵和GINI系数

熵刻画了任意样本集的纯度，熵值越小子集划分的纯度越高［10］，识别其中元组分类所需要的平均信息量就越小。熵的计算公式如下所示式中：pi——样本集S中样本属于类Ci的概率。

对某一连续型描述属性A 的一个分割点T，划分样本集S 的平均类熵为

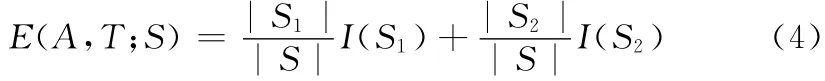
式中：S1——样本集S 在属性A 上取值小于等于T 的子集，S2——大于T 的子集。

在同一二元分裂的情况下，熵和GINI系数的关系如图1所示。由图可知：熵和GINI系数在同一二元分裂中变化趋势相同，熵越小，GINI系数也越小。

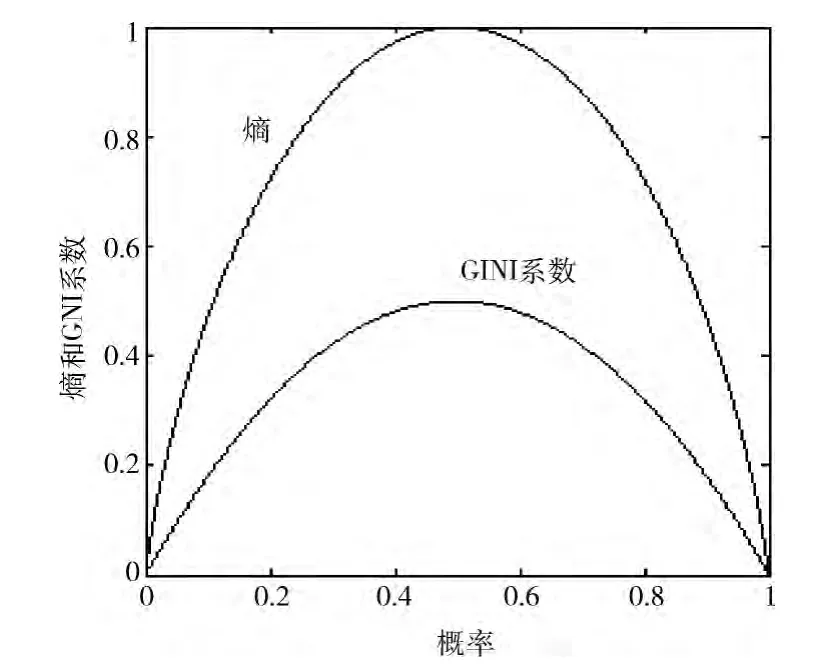
图1 熵和GINI系数的关系

2.3 Fayyad边界点判定原理用于CART算法

比较熵理论和GINI系数可知，熵越小，样本集越纯净，GINI系数也越小。因此，根据Fayyad边界点判定定理：对连续型描述属性A，使GINI系数达到最小值的分割阈值T，也总是处于样本集按属性A 的值升序排列后的属性A 的边界点处。

在CART 算法中，选取连续型描述属性的分割阈值时，不需要计算每个分割点的GINI系数，只要计算分界点的GINI系数即可，GINI系数最小的分界点即为该属性的阈值点。为了保持与CART 的一致性，这里边界点选为排序后相邻不同类别的属性值的平均值。

采用改进的CART 算法，当需要离散化的属性的值越多，而样本所属类别越少时，算法的计算效率提高得越明显；只有在出现最不理想情况时，即每个属性值对应一个类别，改进算法运算次数与未改进算法才会相同，不会降低算法的计算效率［4］。

3 CART算法选择叶节点类标号的改进

决策树在选择叶节点的类别标号时，对叶节点的样本集采取 “多数表决”的方式，即选择多数类作为叶节点的类别标号。但在实际应用中，“多数表决”并不是所有情况都应遵循的唯一准则。本文针对样本集的主类类属分布不平衡时，小类属样本无法表达的情况，利用关键度度量进行改进。与关键度有关的几个定义如下：

定义2 类属分散度：第j个叶节点中的类别i 的样本数占子树总的样本集中类别i的样本数的比重

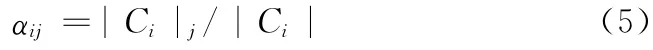
定义3 类属决策度：第j个叶节点中的类别i的样本数占叶节点j的总的样本数的比重

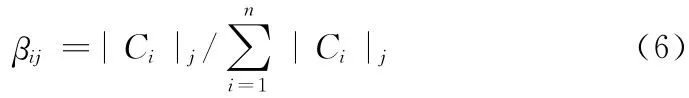
定义4 关键度：其值为类属分散度和类属决策度之积

为了克服偏类样本集中多数类的数量优势，给小类属提供机会展示自己的数据特征，改进的CART 算法在选择叶节点的类别标号时，选取关键度最大的类别标号，而不是选择多数类的类别标号。

4 改进算法核心部分流程

图2和图3分别为选择内部节点的分裂属性的流程和利用关键度度量选择叶节点的类标号的流程，本文主要研究CART 算法选择连续型描述属性分割阈值的改进方法，因此，图2主要针对连续型描述属性。

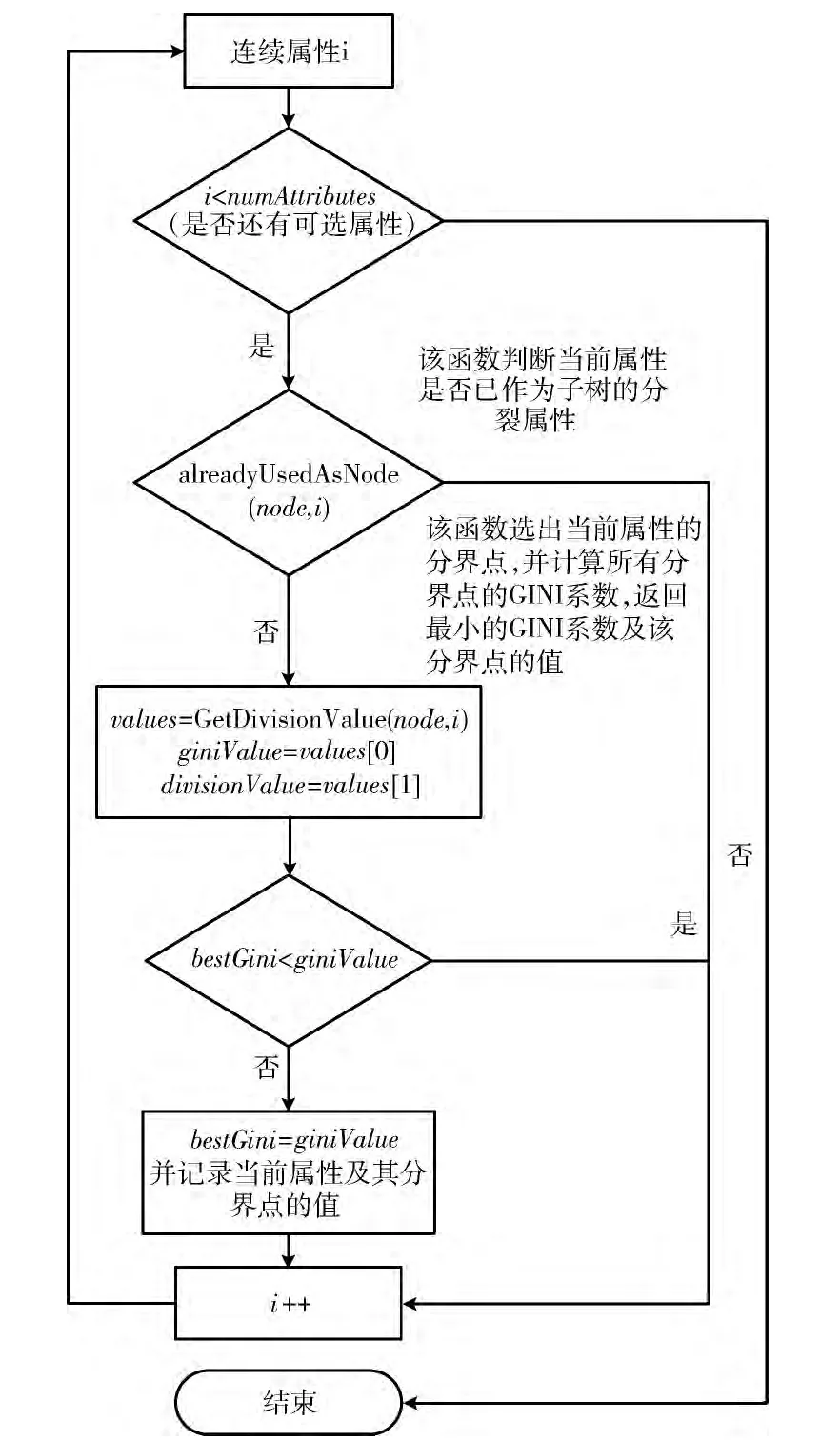
图2 选择内部分裂属性的流程

图3 选择叶节点类标号的流程

5 实验结果及分析

本文 实 验 在Microsoft Visual Studio 2010 平 台 上 进行，算法实现使用C＃语言。实验由两个部分组成：①改进的CART 算法在多样本数，高维度，多类别的故障诊断项目上的应用；②在从标准数据集UCI中采集的部分数据上验证改进的CART 算法的计算效率和分类准确率，实验以CPU 耗时的长短来衡量算法的计算效率的高低。

实验采用10折交叉验证法［11］验证决策树的分类准确率和计算效率。将原始样本集均分成10组，每组样本都包含每类样本的十分之一，将每个样本子集轮流做一次测试集，其余的9 组样本子集作为训练集，这样进行10 次实验，取10次实验的平均分类准确率和CPU 耗时。分类准确率为测试集中被正确分类的样本数占测试集总样本数的比例。

实验1采用某故障诊断系统的样本集，该样本集共包括5620个样本，每个样本有64个连续属性和1个类别属性，共分为10类。实验1用到的样本数据情况见表1。

表1 实验1样本数据情况

实验1对改进的CART 算法和传统的CART 算法在该故障诊断系统中的计算效率和准确率进行了对比，因为该故障诊断系统10个类别的样本几乎均匀分布，不存在主类类属分布不平衡的情况，表2结果表明：在该应用中，改进前后的CART 算法的分类准确率相当，由于改进的CART 算法简化了连续属性选取分割阈值的方法，所以改进后的算法的计算时间缩短了约45%。

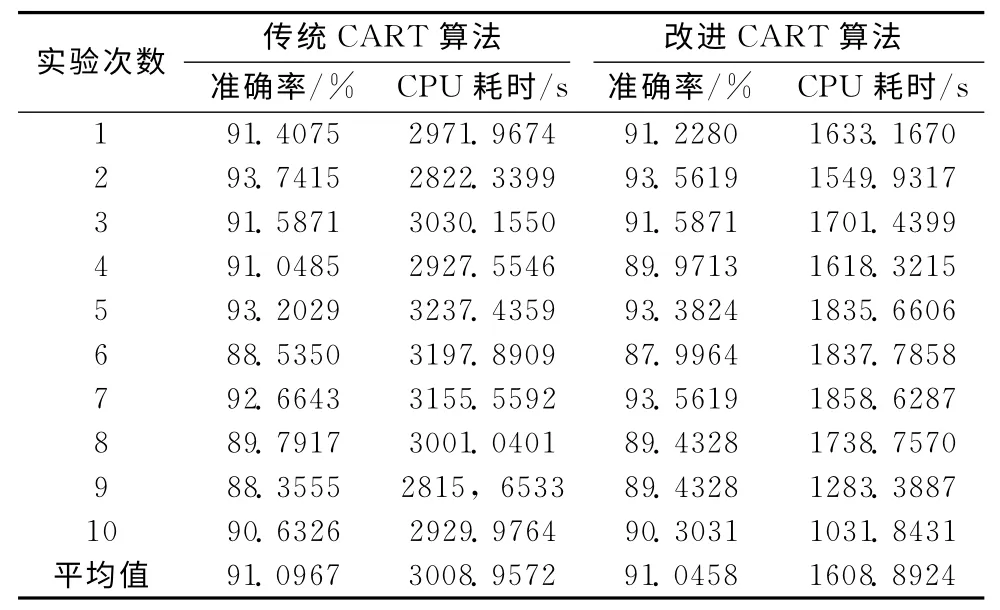
表2 实验1的结果

实验2采用标准数据集UCI中的10组样本集对改进前后的CART 算法的分类准确率和建树效率进行对比，实验2用到的样本情况见表3。表中用＊标注的4个样本集主类类属分布不平衡，这4 个样本集的各类样本分布情况见表4。

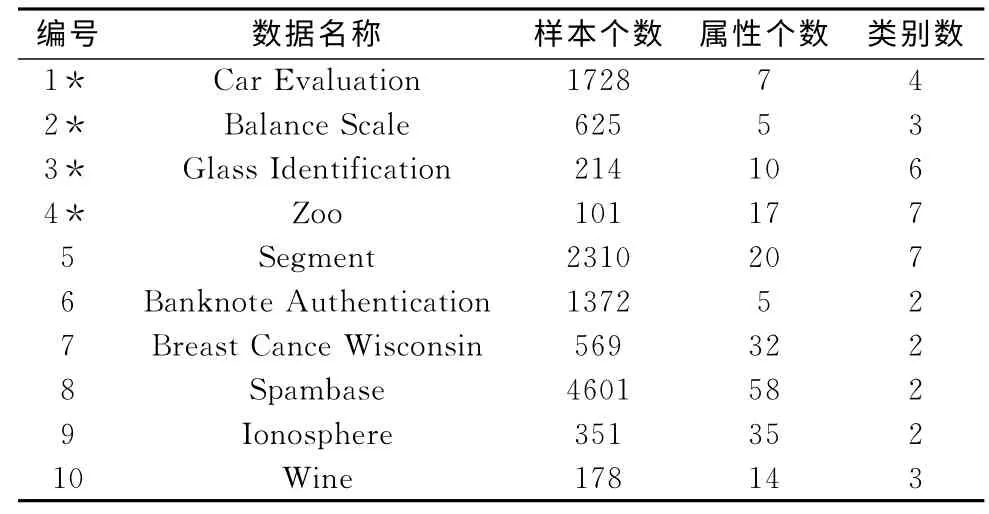
表3 实验2使用的样本集

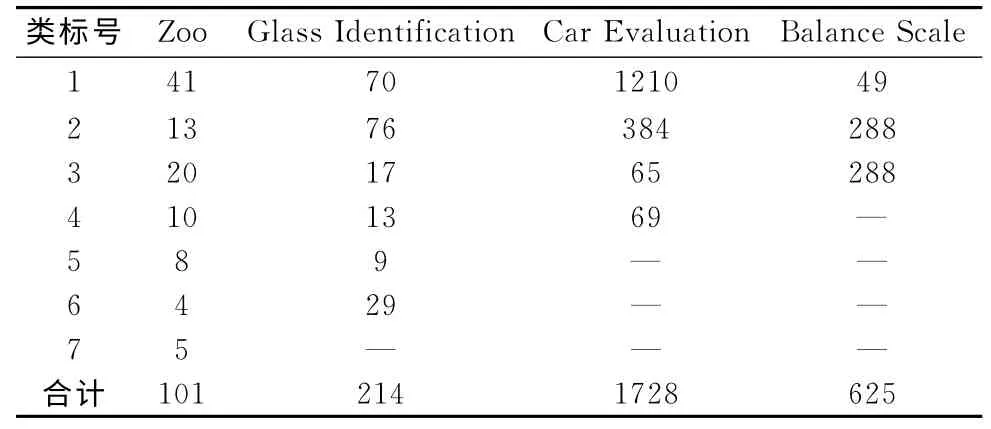
表4 实验2主类类属分布不均的样本情况

实验2的结果见表5。实验2表明：①在主类类属分布不平衡的4个样本集中运用改进的CART 算法，生成决策树的效率得到了提高，分类准确率也略有提高；②对不存在主类类属分布不平衡的样本集，生成决策树的效率提高了，分类准确率与未改进算法的准确率相当。

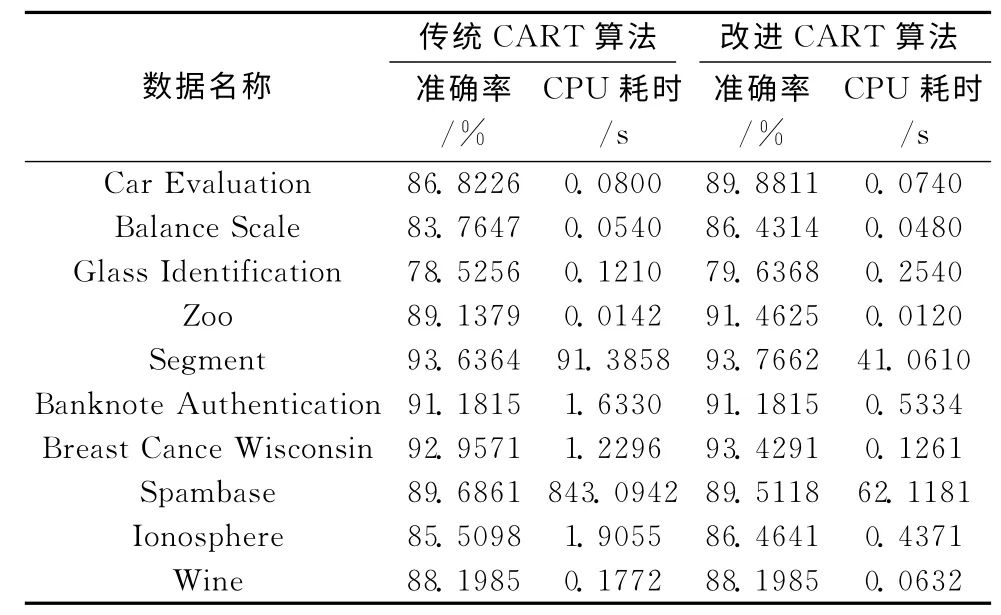
表5 实验2的结果

实验1和实验2的结果表明：①利用Fayyad边界点原理改进CART 算法选取连续属性分割阈值的方法，可以有效提高决策树的生成效率，减少计算量；②对于样本集主类类属分布不平衡的情况，利用关键度度量选取叶节点的类标号，而不是采取 “多数表决”的方式，可以提高分类准确率，使在数量上占少数但并不是稀有的类别可以在分类中得到表现。

6 结束语

结合Fayyad边界点判定原理对CART 算法选取连续属性的分割阈值的方法进行了改进，减少了该算法的计算量，提高了决策树的生成效率。在具有多个连续型描述属性的故障诊断系统中，这一改进具有很好的应用价值。因此，“Fayyad 边界点判定原理”也适用于改进CART 算法选取连续型描述属性分割阈值的方法。结合关键度度量改进了CART 算法选取叶节点类标号的方法，这一改进提高了主类类属分布不平衡的样本集的分类准确率。在部分小样本集上，如本文实验2的第3个样本集，改进前后的算法的准确率都偏低，这是CART 算法的自身缺陷，我们将进一步对小样本集结合其它的分类算法，如SVM 算法，提高小样本集的分类准确率，这将是我们下一步的研究方向。

［1］CHEN Huilin，XIA Daoxun.Applied research on data mining based on CART decision tree algorithm ［J］.Coal Technology，2011，30 （10）：164－166 （in Chinese）.［陈辉林，夏道勋.基于CART 决策树数据挖掘算法的应用研究 ［J］.煤炭技术，2011，30 （10）：164－166.］

［2］ZHANG Beilei.Application of CART algorithm in the analysis of students’achievement ［D］.Hefei：Anhui University，2009 （in Chinese）.［张蓓蕾.CART 算法在学生成绩分析中的应用研究 ［D］.合肥：安徽大学，2009.］

［3］SHAO Fengjing，YU Zhongqing， WANG Jinlong，et al.Principle and algorithm of data mining ［M］.2nd ed.Beijing：Science and Technology Press，2009 （in Chinese）. ［邵峰晶，于忠清，王金龙，等.数据挖掘原理与算法 ［M］.第二版.北京：科学出版社，2009.］

［4］YAO Yafu，XING Liutao.Improvement of C4.5decision tree continuous attributes segmentation threshold algorithm and its application［J］.Journal of Central South University （Science and Technology），2011，42（12）：3772－3776（in Chinese）. ［姚亚夫，邢留涛.决策树C4.5连续属性分割阈值算法改进及其应用［J］.中南大学学报（自然科学版），2011，42（12）：3772－3776.］

［5］LV Xiaoyan，LIU Chunhuang，ZHU Jiansheng.Improved algorithm of decision tree based on key decision factor and its applications in railway transportation［J］.Journal of the China Railway Society，2011，33 （9）：62－67 （in Chinese）. ［吕晓艳，刘春煌，朱建生.基于关键度度量的决策树算法改进及其在铁路运输中的应用［J］.铁道学报，2011，33 （9）：62－67.］

［6］LIU Chunying.A method of generating cost－sensitive decision tree based on correlation degree ［J］.Journal of Changchun University of Technology （Natural Science Edition），2013，34（2）：218－222 （in Chinese）.［刘春英.基于关联度的代价敏感决策树生成方法 ［J］.长春工业大学学报 （自然科学版），2013，34 （2）：218－222.］

［7］ZHANG Nan.Application and research in the identification of latent customers based on improved CART algorithm ［D］.Tianjin：Hebei University of Technology，2008 （in Chinese）.［张楠.改进的CART 算法在潜在客户识别中的应用研究［D］.天津：河北工业大学，2008.］

［8］SUN Xizhou.The application and research of data mining classification technology in fitness club management system ［D］.Qingdao：Ocean University of China，2011 （in Chinese）.［孙喜洲.数据挖掘分类技术在健身会所管理系统中的应用研究［D］.青岛：中国海洋大学，2011.］

［9］QIAO Zengwei，SUN Weixiang.Two improvements to C4.5 algorithm ［J］.Journal of Jiangsu Polytechnic University，2008，20（4）：56－59（in Chinese）.［乔增伟，孙卫祥.C4.5算法的两点改进［J］.江苏工业学院学报，2008，20 （4）：56－59.］

［10］LI Ruping.Research of decision tree classification algorithm in data mining ［J］.Journal of East China Institute of Technology （Science and Technology），2010，33 （2）：192－196 （in Chinese）.［李如平.数据挖掘中决策树分类算法的研究 ［J］.东华理工大学学报（自然科学版），2010，33 （2）：192－196.］

［11］TIAN Jing，AI Tinghua，DING Shaojun.Grid pattern recognition in road networks based on C4.5algorithm ［J］.Journal of Surveying and Mapping，2012，41 （1）：121－126 （in Chinese）.［田晶，艾廷华，丁绍军.基于C4.5算法的道路网网格模式识别 ［J］.测绘学报，2012，41 （1）：121－126.］