基于Sage-Husa方法的旋翼姿态控制
2015-12-23王晓东韦宗毅
王晓东,马 磊,韦宗毅
(西南交通大学 电气工程学院,四川 成都610031)
0 引 言
实时获取精确的姿态信息是实现旋翼飞行器自主飞行的首要前提。用于姿态解算的陀螺仪传感器更新频率越高越有助于提高姿态解算精度,但高频数据更新也会带来两个问题:①随机噪声影响更显著;②计算复杂度呈指数增长,难以满足实时性。文献 [1]通过一种增益可调的互补滤波器融合陀螺仪及加速度计姿态角度信息,实时性好但模型辨识度低;文献 [2]通过卡尔曼滤波器解算当前飞行姿态,但系统传递噪声难以事先估算;文献 [3]使用粒子滤波算法实现陀螺仪与加速度计姿态融合,算法复杂度大,难以满足实时性要求;文献 [4]通过基于四元数的自适应卡尔曼滤波器获得姿态角度,模型线性化过程引入误差,影响姿态解算精度。
本文首先设计噪声滤波模型以抑制传感器随机噪声,之后通过自适应信息融合滤波算法获得姿态角度。建立ARMA (auto-regressive and moving average model)模型将有色噪声白化,并通过基于ARMA 模型的卡尔曼滤波器抑制陀螺仪噪声。之后,为获得更精确的姿态角度,建立卡尔曼滤波器融合两者传感器信息。为提高系统的自适应性,采用Sage-Husa自适应方法优化融合滤波算法;为弥补Sage-Husa方法容错性差的缺陷,本文提出一种加速度计可信性判别条件,避免Sage-Husa方法将观测噪声带入姿态解算系统。
本文通过以上方法提高了姿态解算系统的模型精确度,并将该系统搭载在四旋翼半实物仿真平台上,以验证该系统的实际效果。
1 卡尔曼滤波器及本文中的应用
本文工作中陀螺仪信号降噪、姿态解算使用了卡尔曼滤波器。通过建立ARMA 模型并增广卡尔曼滤波器系统状态方程,估计当前信号的同时通过时间序列分析估计当前噪声序列,从而将有色噪声白化;由于陀螺仪与加速度计的信息融合模型具有时变性大、野值出现频率高等特点,本文将Sage-Husa方法应用于姿态融合的卡尔曼滤波器以增强姿态解算系统的自适应性,并提出一种新的加速度信息可信性条件以增强系统容错性。
卡尔曼滤波的基础算法如式 (1)~ (5)所示[5]。
步骤1 状态一步预测
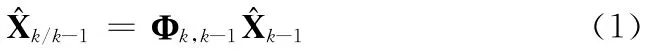
步骤2 一步预测均方误差
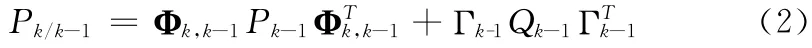
这里Qk代表系统噪声的方差矩阵。
步骤3 滤波增益更新
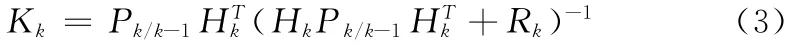
这里Rk代表观测噪声的方差矩阵。
步骤4 状态估计
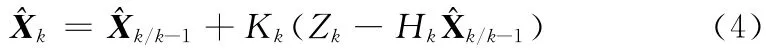
步骤5 估计均方误差Pk的实时更新
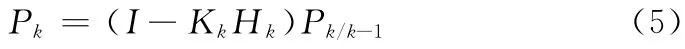
2 传感器信号噪声分析及抑制
选用Analog Devices 公司的ADIS16405 传感器,该IMU 内置了三轴陀螺仪与三轴加速度计。数据更新频率为819.2Hz,陀螺仪测量精度为0.0125°/sec,加速度计测量范围是±8g,分辨率为3.33mg。
对传感器原始数据降噪处理,通过四元数法及受力分析将角速度和加速度值转换为相应的姿态角度。使用单个传感器获得的姿态可靠性较低,其中陀螺仪输出角速度信息,积分得到的姿态角信息存在累积性偏差,导致解算角度偏离真实角越来越大;加速度计对环境噪声敏感,高频噪声较大。为此,设置信息融合滤波器求解传感器的俯仰角和横滚角姿态。为确保信息融合滤波效果,该融合滤波器需要有针对性地抑制陀螺仪积分噪声,并根据加速度计所包含运动加速度的多少适时调整加速度计可信性条件。
2.1 传感器噪声分析
通过分析得知陀螺仪噪声为平稳的高斯有色噪声,加速度计噪声为平稳的非高斯有色噪声。
对于平稳、高斯分布的陀螺仪噪声,使用卡尔曼滤波器抑制噪声,由于陀螺仪噪声属于有色噪声,在低频段功率密度较大,建立ARMA 模型将陀螺仪有色噪声白化,并采用基于ARMA 模型的卡尔曼滤波器抑制陀螺仪噪声。对加速度计噪声使用低通滤波器抑制噪声。
2.2 基于ARMA模型的卡尔曼滤波器陀螺仪降噪
针对陀螺仪噪声,进行自相关与偏自相关检验后,利用时间序列分析法建立 (5,3)阶的ARMA 模型[6],如式(6)所示
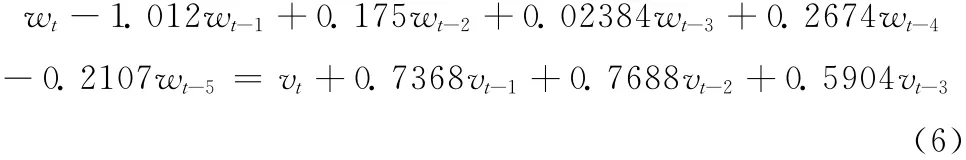
式中:{wt}表示有色噪声序列,等式左边的序列亦可称为AR 模型,描述该函数的偏自相关特性;{vt}表示与{wt}相对应的均值为0、标准差为σ的白噪声序列,等式右边的序列称为MA 模型,描述该时间序列的自相关特性。
使用卡尔曼滤波器抑制该类随机噪声,并增广该滤波器的状态方程,将得到的ARMA 噪声模型 (式 (6))也作为状态方程的一部分,获得系统状态方程如式 (7)所示
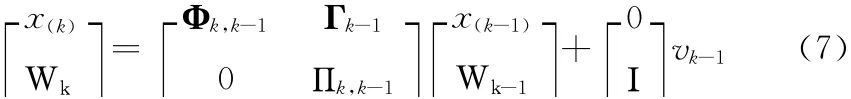
式中:x(k)——陀螺仪输出信号的估计, Wk=…,代表陀螺仪的AR 噪声序列,vk表示均值为0 标准差为σ的MA 模型噪声序列;Γk=表示噪声驱动矩阵;Πk,k-1表征与Wk对应的序列参数传递矩阵。
状态增广后的量测方程为
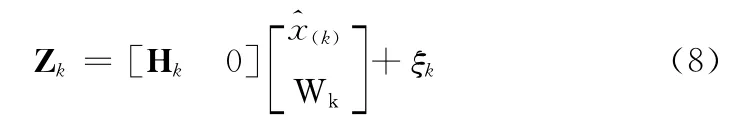
式中:Zk表征当前观测结果,Hk=[1],ξk 序列表征均值为0标准差为σ′的噪声序列。
根据式 (1)~式 (5)算法实现卡尔曼滤波算法。经过降噪滤波器后,将陀螺仪噪声方差降低为原始噪声的3.09%,实际飞行过程中滤波效果如图1 所示。在保证有效信号不丢失的同时,有效抑制了原始数据的波动性,提高了数据准确性。
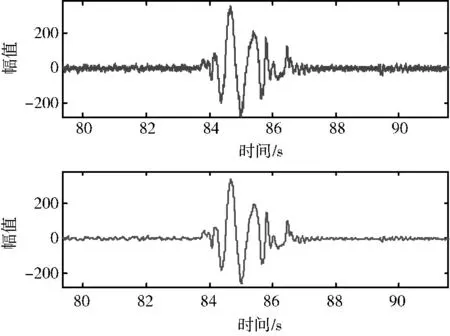
图1 陀螺仪滤波前后数据对比
3 姿态信息融合滤波器设计
3.1 基于Sage-Husa方法的卡尔曼滤波
获得降噪后的三轴角速度信息后,通过四元数法更新姿态角度信息。为了便于姿态控制将四元数姿态角度最终转换为欧拉角[7],将姿态信息表示为 “东-北-天”导航坐标系下的航向角φ,俯仰角θ,横滚角ρ信息。相应地,采用基于一个参考点确定加速度计各个轴角度的方法,获得加速度计相应的俯仰角和横滚角信息。
设计信息融合滤波器,利用陀螺仪对角速度的精确测量以及加速度计低通信号有效性以获得更精确的姿态结果。加速度计俯仰角、横滚角分别为θacc、ρacc ,陀螺仪获得的俯仰角和横滚角分别为θgyro、ρgyro。两者传感器获得的姿态值之间有如下关系式
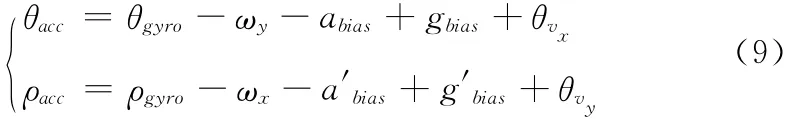
其中,ωx与ωy分别代表陀螺仪X 轴、Y 轴检测到的零偏随机噪声的积分信息,该随机噪声的均值不为零,数据波动性较小;abias、a′bias表示加速度计在两轴上的零均值噪声;gbias、g′bias表示陀螺仪在两轴上的零均值噪声;θvx、θvy表示加速度计X 轴、Y 轴检测到的线运动加速度分量的作用力。
当运载体近似静止或匀速运动时,vx→0、vy→0,可忽略不计。根据式 (9)可获得用于信息融合的卡尔曼滤波器系统方程

其中,τbias与τ′bias表示均值为零的高斯噪声序列,分别作为ωx、ωy零偏随机噪声的一阶马尔科夫过程,表示状态传递矩阵。
在卡尔曼滤波算法实时更新式 (1)~ (5)的同时,鉴于加速度计噪声属于非高斯信号,导致融合滤波器姿态控制系统的观测噪声方差具有时变性,需要增强融合滤波器的自适应性,采用带观测噪声时变估值器的简化Sage-Husa自适应算法[8]优化信息融合滤波器。在式 (1)~(5)的基础上,增添了观测噪声实时估计方程,如式 (11)所示,通过Sage-Husa方法实时更新系统的观测噪声
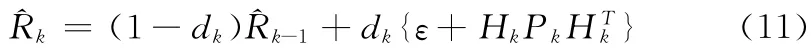
式中:ε=(I-HkKk)YYT(I-HkKk)T表示当前估计获得的观测噪声协方差矩阵,dk表示衰减因子,Hk表征观测矩阵、Kk表征滤波增益、Y =Zk-Hk表征当前残差。
3.2 加速度计可信性条件
为避免实时观测过程中野值影响Sage-Husa方法估计结果的准确性,增强系统容错性,提出一种新的加速度计可信性条件,不仅考虑载体当前所受总加速度大小的时候,还估量当前总加速度与重力间的相对方向。由于本文主要研究的是旋翼悬停状态时的姿态控制问题,当Z 轴加速度方向与重力方向相同时加速度姿态角度更为可信,若加速度计输出信息包含过多的运动加速度信息时,不使用信息融合滤波更新姿态,仅依靠陀螺仪角速度信息。
判别加速度计信息是否可信的阈值条件ζ定义如下
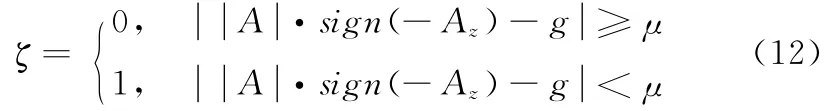
综上所述,当进行姿态更新时,首先进行加速度计可信性判断,若加速度计可信则通过基于自适应卡尔曼的信息融合滤波器获得姿态结果,将其作为最终的姿态解算结果;若加速度计不可信则将陀螺仪姿态作为最终姿态结果。
4 实验测试
4.1 硬件构架
采用基于ARM Cortex M4内核的STM32F417作为控制芯片。自制四旋翼半实物仿真平台,由四旋翼飞行器机架、电子调速器、电机及万向节轴承底座组成。万向节与轴承使得四旋翼能够在水平方向360°水平旋转,在俯仰及横滚方向±90°旋转。仿真平台如图2所示。
姿态解算和控制系统按照功能划分为传感器ADIS16405、遥控器、STM32主控芯片、四旋翼飞行器半实物仿真平台、存储模块、上位机等6个模块。硬件结构框架如图3所示。
为了验证姿态确定系统的可行性,在得到四旋翼的三维姿态后,建立四旋翼飞行器动力学模型[1,10],并控制四旋翼飞行器的姿态[11]。
4.2 实验及结果

图2 四旋翼飞行器半实物仿真平台
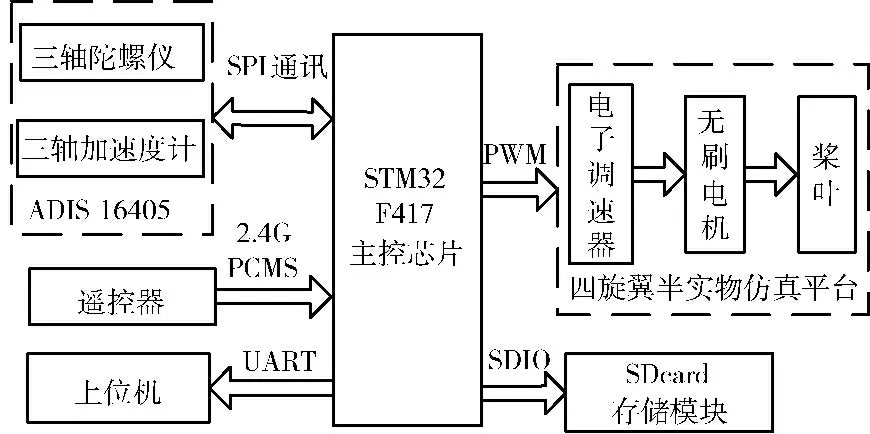
图3 硬件结构框架
首先进行姿态融合滤波测试。采集四旋翼飞行器实际飞行中垂直起降及悬停的原始数据,通过SDcard分别存储单独使用陀螺仪、单独使用加速度计、姿态融合滤波器的输出结果。
在ARM 芯片上通过设置相应的浮点运算单元 (FPU)实现正确高效的浮点运算。ADIS16405传感器采样周期为1.22ms。通过设置相应的外部中断及定时器中断管理程序进程,缩减程序执行时间。实际测试结果显示,三轴陀螺仪通过3个6维卡尔曼滤波器滤波,三轴加速度计通过3个2阶卡尔曼滤波器滤波,降噪模块共耗时363.9μs;信息融合滤波模块包含可信性判别及2个2阶卡尔曼滤波器共耗时244.83μs。平均进行一次姿态确定及控制程序的执行周期为711.3μs,远小于姿态控制周期。
根据实际测试数据绘制改进算法与常规融合滤波算法对比如图4所示,半实物仿真平台上旋翼飞行器保持平衡状态,21s时人为给予机架-10°偏角。第1小图与第2小图是使用本文算法获得的姿态结果与常规融合算法比较,第3小图变量幅值为1时表示未进行姿态融合滤波,仅依靠陀螺仪数据更新姿态。
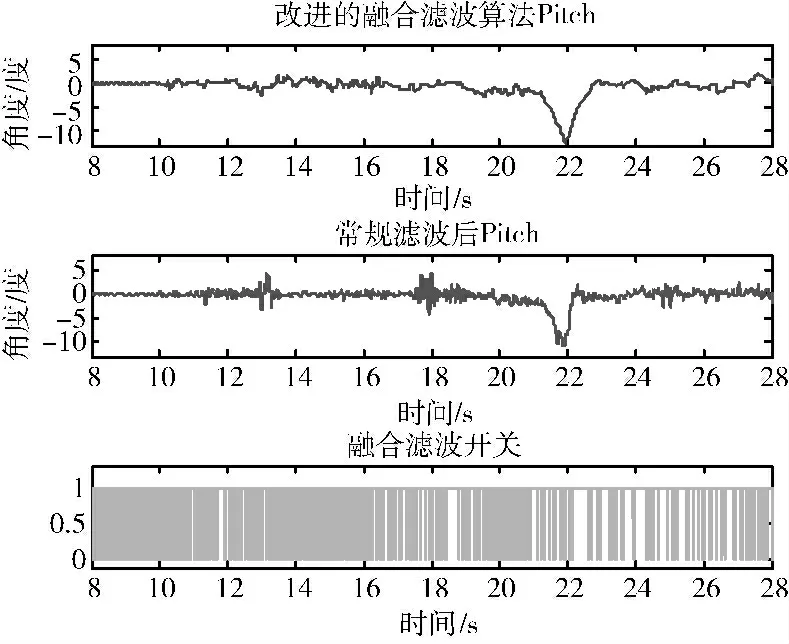
图4 改进算法与常规融合滤波算法比较
由图4可以看出,在13s及18s附近,未使用自适应算法获得的姿态解算结果存在轻微晃动,如图5所示是统计10s~21s各秒内姿态角度方差后作出的对比,由方差对比可知改进的融合算法姿态解算精度效果远好于常规融合滤波算法;由21s人为干扰后姿态解算结果对比,改进的融合算法对姿态变化更敏感,对运动过程中噪声的抑制性更强。
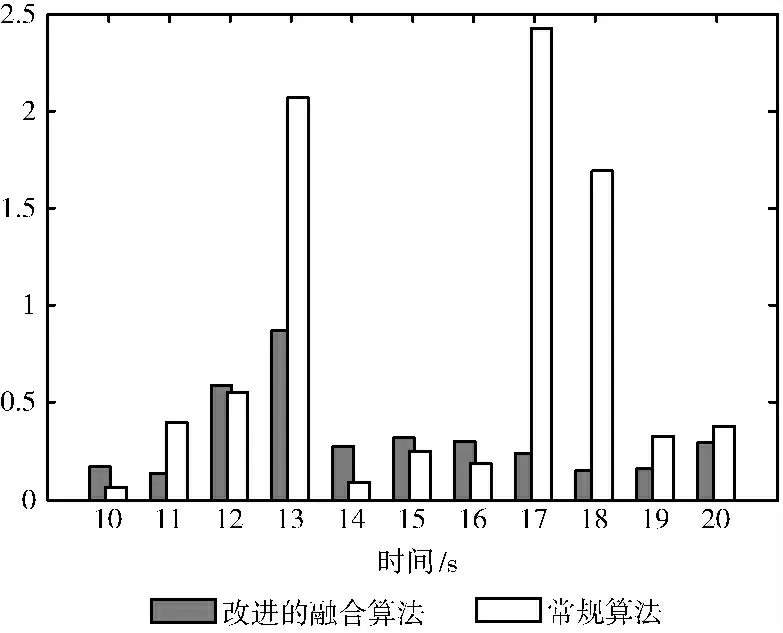
图5 平稳姿态方差对比
通过以上分析得到结论:应用Sage-Husa方法增强姿态解算系统自适应性,并使用加速度计可信性条件后,姿态解算系统对当前环境的自适应性更高,能够获得更精确的姿态结果。
姿态控制采用PID 算法,通过半实物仿真平台检验实际控制效果。在上电前给予四旋翼飞行器俯仰角和横滚角一定的初始偏角,记录上电后四旋翼飞行器恢复俯仰角0°、横滚角0°所需的时间;在平衡状态下,多次给予飞行器幅度不同的人为扰动,记录飞行器由扰动后姿态到恢复平衡位置所需的时间。俯仰角及横滚角实测数据如图6所示。
人为干扰后,四旋翼飞行器的姿态角度回复到平衡位置的时间最快为0.39s,最慢为0.88s。由以上实验验证了姿态控制系统的优越性,该系统反应迅速、抗干扰性强。
5 结束语
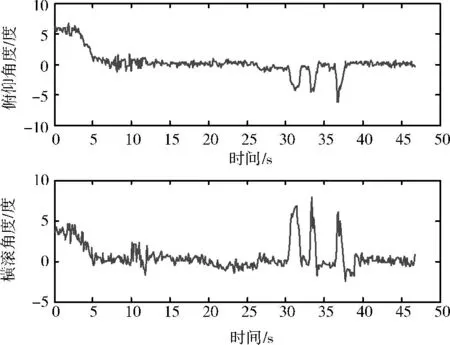
图6 半实物仿真平台实测数据
该姿态控制系统以基于ARM Cortex M4内核的嵌入式系统为硬件平台,通过基于Sage-Husa方法的卡尔曼滤波器以及相应的加速度计判别条件,提高姿态解算系统的自适应性的同时也避免了传统方法实时估计观测噪声而引入野值误差。本方法提高了模型的精确程度以及姿态结果的精度和可靠性。该姿态解算及控制系统针对陀螺仪与加速度计固有特点,抑制了陀螺仪噪声的随机漂移的同时也降低了姿态结果的波动性。四旋翼半实物仿真平台实际测试结果表明,该系统能够实时获取可靠的姿态信息,满足四旋翼飞行器系统的姿态控制精度需求。
[1]Mahony R,Kumar V,Corke P.Multirotor aerial vehicles:Modeling,estimation and control of quadrotor [J].Robotics&Automation Magazine.IEEE,2012,19 (3):20-32.
[2]Tomic T,Schmid K,Lutz P,et al.Toward a fully autonomous UAV:Research platform for indoor and outdoor urban search and rescue [J].Robotics & Automation Magazine.IEEE,2012,19 (3):46-56.
[3]QU Shiru,MA Zhiqiang.Application of the improved particle filter to quad-rotor aircraft’s attitude estimation[J].Flight Dynamics,2013,31 (5):458-461 (in Chinese). [曲仕茹,马志强.改进的粒子滤波在四旋翼姿态估计中的应用 [J].飞行力学,2013,31 (5):458-461.]
[4]Suh YS.Orientation estimation using aquaternion-based indirect Kalman filter with adaptive estimation of external acceleration [J].IEEE Transactions on Instrumentation and Measurement,2010,59 (12):3296-3305.
[5]Aanonsen SI,Nvdal G,Oliver DS,et al.The ensemble Kalman filter in reservoir engineering-a review [J].Spe Journal,2009,14 (3):393-412.
[6]Erdem E,Shi J.ARMA based approaches for forecasting the tuple of wind speed and direction [J].Applied Energy,2011,88 (4):1405-1414.
[7]Do KD,Paxman J.Global tracking control of quadrotor VTOL aircraft in three dimensional space [C]//3rd Australian Control Conference,2013:26-33.
[8]Zheng Z,Shirong L,Botao Z.An improved Sage-Husa adaptive filtering algorithm [C]//31st Chinese Control Conference,2012:5113-5117.
[9]Bouabdallah S.Design and control of quadrotors with application to autonomous flying [J].Ecole Polytechnique Federale de Lausanne,2007.
[10]HAN Zhifeng,LI Rongbing,LIU Jianye,et al.Model optimization of small quad-rotor in the case of center of mass offset[J].Control Engineering of China,2013,20 (S1):158-162.(in Chinese).[韩志凤,李荣冰,刘建业,等.小型四旋翼飞行器动力学模型优化 [J].控制工程,2013,20(S1):158-162.]
[11]Liu H,Bai Y,Lu G,et al.Robust tracking control of a quadrotor helicopter [J].Journal of Intelligent & Robotic Systems,2013:1-14.
