基于限制等距性质阈值机制的匹配追踪算法

黄宏伟，谢正光，蒋小燕，蔡 旭

（南通大学 电子信息学院，江苏 南通226019）

0 引 言

近几年一种高效的信号采集技术压缩感知 （compressed sensing，CS）［1］逐渐被人们学习了解。它的模式是边采集边压缩，即在数据采集过程中就进行适当的压缩，这样信号采集速度能低于奈奎斯特采样速度，节省大量资源［2，3］。

压缩感知测量过程可以用方程描述为y ＝Φx，其中y是长度为M 的观测信号，Φ ＝［，…］是测量矩阵，大小为M×N ，x为K 阶稀疏信号，长度为N，K ＜M ＜N，这个过程相当于把原始信号投影到［，…］张成的空间上［4］。

压缩感知中重构算法是核心内容，是从测量矩阵Φ和观测信号y中恢复原始稀疏信号x。这个过程可以当作l0最小化问题来求解：x＝argmin x0subject to y＝Φx，理论上，没有噪声的前提下，K 阶稀疏信号仅需M ≥2 K 次测量就可以恢复。但是l0最小化问题是NP－hard问题。Donoho和Candes指出不必求助于l0解稀疏解，而是通过一个更简单的l1最优化方法：x ＝argmax x1subject to y ＝Φx，但是要求Φ满足RIP［5］。虽然线性规划方法重构效果很好，但是它的高复杂度限制了其实际应用，这就要求我们设计一种快速的求解方法。

贪婪算法因为其较低的复杂度而受到越来越多人的关注。包括匹配追踪 （matching pursuit，MP），OMP［6－8］、正则化正交匹配追踪 （regularized OMP，ROMP）［9］、分段式正交匹配追踪 （stagewise OMP，StOMP）、压缩采样匹配追踪算法 （compressive sampling matching pursuit，Co－SaMP）［10］、SP［11］等等。这些方法的基本思想是通过相关性从不相关的原子中寻找正确的支撑集，每一个迭代过程都是从原子序列中找出认为足够相关的原子索引并添加到支撑集中。MP算法每次寻求的是局部的最优解，虽然执行速度快，但是最终不一定收敛到全局最优，所以重构精度不是很高。带有回溯思想的SP算法有两个特征，一是当信号非常稀疏时，SP 算法比OMP 算法计算复杂度低；二是SP算法的重构精确度与LP 方法相当［11］。但是，SP 算法没有考虑代理信号和残差关系，每次迭代都选择K 个原子，这可能导致迭代过程中选择错误支撑集数目增多。经典的OMP算法有两个缺点：第一是每次选择的最大相关原子不一定是正确原子；第二是每次迭代添加的支撑集原子索引都是不会被移除的，即无自主纠错能力。针对OMP这两个缺点，我们提出RIPTMP 算法的原子选择方案。RIPTMP首先根据RIP和残差条件一次选出多个原子，其次算法能够根据信号特点剔除可能错误的原子。在该方案下，算法提高了寻找支撑集的精度。

1 RIPTMP算法

1.1 符号标注

首先简单说明本文涉及的符号。supp（x）表示向量x 中非零元素的位置，即向量x 的支撑集。K 表示稀疏度。ΦT表示Φ的转置，T0定义为初始的支撑集，表示初始的残差，Tl表示第l次迭代得出的支撑集，表示Tl的补集。表示第l次迭代得出的信号残差，表示x 对应Tl位置上的元素集合。ΦI表示I 中所有索引对应原子的集合，如果ΦI可逆，那么yp表示y 在ΦI上的投影yp＝＜y，，其中，代表ΦI的伪逆。δK＋1为K＋1阶RIP常数，表示第l次迭代的代理信号表示代理信号中的元素，其中＜·＞表示内积运算，ei为单位矩阵的第i列。

1.2 RIPTMP算法流程

RIPTMP算法在原子选择上带有回溯思想，经典的SP算法也具有同样思想。SP算法需要待重构稀疏信号的稀疏度K。算法在每次迭代过程中，原子添加的和删减的数量都为K。具体算法见表1。

表1 子空间追踪算法

SP有两个缺点，一方面在原子选择数量上没有考虑残差变化，每次选取的数量为固定值K，这就可能导致当前选择多个错误的原子，从而引起重构精度下降；另一方面算法需要待重构稀疏信号的稀疏度。

RIPTMP算法除了需要测量矩阵Φ和观测信号y，还需要算法停止参数ε，支撑集添加阈值E，支撑集保持阈值P，和最大迭代次数imax。算法具体流程见表2。

表2 基于RIP阈值机制的匹配追踪算法

1.3 RIPTMP算法分析

RIPTMP算法中有两个参数，E 和P。下面我们给出这两个参数选择依据：

1.3.1 预备知识

（1）有限等距性质 （RIP）定义［11］

如果矩阵Φ ∈RM×N满足参数为 （K，δ）的有限等距性质，K ≤M ，0≤δ＜1。对于任意的k 阶稀疏信号x ∈

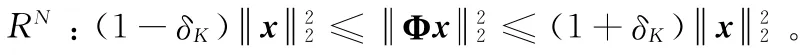
（2）最大相关选择原理

假设Φ的所有列向量都是完全正交的，即Φ为正交矩阵，那么所求代理信号系数＜，y＞中非零值对应的位置就是原信号的支撑集。但是大部分Φ中列向量都不是完全正交的，（1）说明满足RIP条件的Φ近似为正交矩阵，这时候最大相关系数对应的位置索引不一定在原信号支撑集中。但是，正确原子和观测信号的相关系数和非正确原子和观测信号的相关系数是有界的。因此我们可以根据相关系数的界寻找支撑集。

（3）引理

引理1［9］对于任意的两个正整数m≤n，有δm≤δn。

引理2［5］设supp（x），supp（y）｛1，2，…N｝，｜supp（x）｜≤m，｜supp（y）｜≤n，supp（x）∩supp（y）＝，那么｜＜Φx，

引理3 设向量x∈RN，｜supp（x）｜≤m，那么

1.3.2 E，P参数估计

第一次迭代：

假设矩阵Φ∈RM×N满足参数为 （K ＋1，δ）的有限等距性质，根据引理2 有：isupp（x），｜h1（i）｜＝｜＜

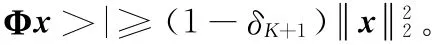
同理对于第l次迭代

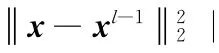
结合第一次迭代和第l次迭代，我们把i∈supp（x）的｜hl（i）｜和jsupp（x）的｜hl（j）｜的界进行估计。即对于任意jsupp（x），有

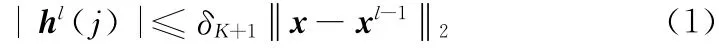
通过上面推导过程可以发现E 和P 的边界条件经过了放缩，E估计的界是在实际的界基础上进行了放大，P 估计的界是在实际界的基础上进行了缩小，因此在实验仿真阶段可以在估计出来的界基础上适当的放缩。

虽然RIPTMP算法是鉴于SP算法两个缺点提出来的，但是它的理论基础却来源于OMP 算法。OMP 算法每次迭代只选择最相关的原子，同时选择的原子不会被移除，而实际上，最相关原子不一定是正确原子，当算法引入了错误原子时应该通过回溯过程进行剔除。因此，我们先把所有可能正确的原子都选出来，然后再剔除可能错误的原子。通过理论分析，添加和删减原子的数量和残差，RIP 常数密切相关，所以我们通过残差和RIP 常数条件求出相应阈值来筛选原子。

2 实验

为了全面测试算法重构性能，对一维信号和二维信号都进行了相关实验。在一维信号部分，选择了3种不同类型的稀疏信号分别为高斯信号， “0－1”信号和均匀分布信号。二维信号则是标准的Lena，Boat测试图像。

2.1 一维信号仿真实验

令测量矩阵为标准正态分布矩阵，测量次数M＝128，信号长度N＝256。OMP 和RIPTMP 迭代停止阈值相同，均取ε＝10－6，RIPTMP 的最大迭代次数imax＝0.5 M，BP算法重构通过cvx工具箱实现。FBP 算法给前长步长α＝0.3 M，后退步长β＝α－1，停止阈值ε＝10－6，最大迭代次数imax＝0.5 M。实验中RIPTMP 算法有3种不同的设置，分别是（E＝0.2，P＝0.7）、（E＝0.1，P＝0.6）、（E＝0.1，P＝0.4）。重构成功条件：均方误差，实验次数times取500。

实验结果如图1所示。

2.2 二维信号仿真实验

为了衡量算法对稀疏图像信号重构性能，选择标准的256×256的Lena，Boat作为测试图像。随机产生大小为M×N 的测量矩阵Φ，Φ为归一化的准高斯矩阵，对图像信号进行小波变换选择sym6小波基。保留小波变换后系数矩阵每列最大的q个小波系数，其余置零。峰值信噪比计算

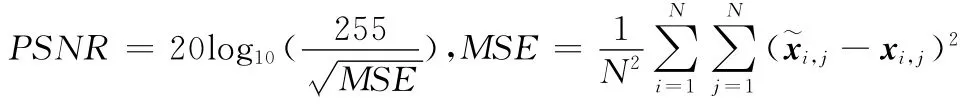
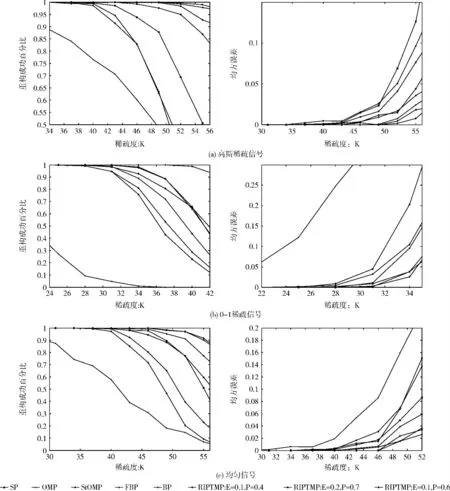
图1 一维信号仿真实验

分别用SP，BP，RIPTMP，FBP这4种重构算法重构图像信号，其中SP稀疏度设置为q，RIPTMP参数设置为（E＝0.1，P＝0.6），FBP停止参数和最大迭代次数相同。重构结果如图2所示。

图2 二维信号仿真实验

2.3 实验结果分析

（1）一维信号重构实验

在图1 （a）高斯信号仿真实验中，E＝0.2，P＝0.7的RIPTMP算法的重构误差比OMP，SP 低，成功重构概率明显高于OMP，SP算法。SP成功重构概率从K＝40开始下降，而RIPTMP从K＝43才开始下降。当我们把前面推导并估计出的界E 适当收缩到0.1，同时P 放大到0.6，RIPTMP效果明显提升。一方面重构均方误差低于包括BP在内的其它所有算法，当K＝50才由0逐步上升，而且在稀疏度取值区间［1，2，3...56］内都保持较低的值；另一方面成功重构概率在相同稀疏度条件下比其它算法都要高，当稀疏度达到52 以上时，才出现重构失败情况。参数为（E＝0.1，P＝0.4）的RIPTMP 重构情况和参数为 （E＝0.1，P＝0.6）RIPTMP重构情况相当。

在图1 （b）“0－1”信号实验中，OMP效果最差，从仿真数据可以看出 （为了方便显示，曲线前面部分经过适当省略），当稀疏度到10左右误差就开始从0开始上升，而其它算法依然保持0的水平。当K 增加到25左右SP算法和参数为 （E＝0.2，P＝0.7）的RIPTMP 和StOMP 重构误差开始从0增加，到K 增加到28左右，SP和FBP算法误差开始从0上升。当K 增加到31左右参数为 （E＝0.1，P＝0.4）和 （E＝0.1，P＝0.6）的RIPTMP算法重构误差开始从0上升。对应的重构百分，OMP从K＝8处重构开始出现失败。参数为 （E＝0.2，P＝0.7）和StOMP 算法从K＝28处重构开始出现失败。当K 增加到29 时，FBP和SP出现重构失败情况。当K 达32左右，参数为 （E＝0.1，P＝0.4）和 （E＝0.1，P＝0.6）的RIPTMP 算法出现重构失败。BP算法重构结果最好。

在图1 （c）均匀信号实验中，RIPTMP 算法重构误差明显小于OMP，接近BP 算法。参数为 （E＝0.1，P＝0.4）和 （E＝0.1，P＝0.6）的RIPTMP 算法在稀疏度［1，2，3…52］区间内重构的均方误差和BP 算法相差不大，紧接着是SP算法，参数为 （E＝0.2，P＝0.7）RIPTMP算法等等。重构百分比曲线上可以得出参数为 （E＝0.1，P＝0.6）和 （E＝0.1，P＝0.4）的RIPTMP 算法在稀疏度达到46 才开始下降，紧接着是FBP 算法、参数为（E＝0.2，P＝0.7）RIPTMP算法、SP算法等等。

实验说明，RIPTMP 算法在一定条件下，相比OMP，StOMP，SP，FBP算法有更高的重构精度和重构成功概率。虽然E，P参数推导过程得出相同的阈值条件，但是E＝P≈0.4的阈值条件并不是准确的。E推导的界比真实的界大，P推导的界比真实的界小，因此适当改变E，P可以得出精度更高的支撑集估计效果，实验部分正好证明了这一点。

（2）二维信号重构实验

图2中，我们列出了SP，BP，FBP 和RIPTMP 算法重构效果。Lena图像重构实验中，SP算法重构信号的峰值信噪比为32.3dB，BP为33.4dB，FBP为33.2dB，参数为 （E＝0.1，P＝0.6）的RIPTMP 为33.4dB。Boat图像重构实验中，SP 算法重构信号的峰值信噪比为31.7dB，BP为32.0dB，FBP 为31.8dB，参数为 （E＝0.1，P＝0.6）为32.0dB。可以看出RIPTMP算法的峰值信噪比高于SP算法，当E＝0.1，P＝0.6时，达到了BP算法水平。FBP 算法峰值信噪比也接近BP 算法，略低于RIPTMP算法。

二维图像信号重构中，虽然用小波变化对图像进行稀疏化处理，但是得到的并不是严格的稀疏矩阵。因此我们对小波变化后的矩阵进行了处理，即保留小波变换后系数矩阵每列最大的q 个小波系数，其余置零。因为测量矩阵的列向量不是完全正交的，所以可能导致数值较小的小波系数所在列的索引被当成重要的原子来重构，而真正大的小波系数被忽略，这就会影响重构的精度。在信号重构部分，经典的SP算法需要稀疏度条件，而图像稀疏化过程中如果不进行特定的处理不能获取稀疏度的条件，因而不能确定每次迭代选取原子个数。RIPTMP 算法是通过最大迭代次数控制迭代过程，在稀疏度较小的时候，经过很少的迭代就可以找出所有的原子，因此我们并不需要待重构稀疏信号的稀疏度。所以，二维图像信号重构上RIPTMP 算法比SP算法更加合理。FBP算法虽然不需要稀疏度条件，但是每次更新原子的步长是不变的，前长步长α＝0.3 M ，后退步长β＝α－1。这种选择原子同样没有考虑信号残差的变化因素，且前向步长的确定条件并没有给出理论依据，而RIPTMP 给出原子选择的依据，而且仿真效果好于FBP，因此更合理。

3 结束语

本文基于SP算法重构精度低，需要已知稀疏度的缺点提出RIPTMP算法。首先算法在寻找支撑集上和SP不同，RIPTMP算法是根据RIP条件估计正确支撑集代理信号的幅值范围，选出所有满足的原子，而不是仅仅只选择代理信号的最大值对应的原子。其次，算法不需要稀疏度作为算法输入条件。实验结果表明，在一定条件下RIPTMP 算法重构精度高于OMP，SP，FBP 等经典算法，达到了BP算法水平，而且算法不需要待重构信号稀疏度。

［1］Candès E J，Wakin M B.An introduction to compressive sampling ［J］.Signal Processing Magazine，IEEE，2008，25（2）：21－30.

［2］SHI Guangming，LIU Danhua，GAO Dahua，et al.Advances in theory and application of compressed sensing ［J］.Acta Electronica Sinica，2009，37 （5）：1070－1081 （in Chinese）. ［石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，37 （5）：1070－1081.］

［3］DAI Qionghai，FU Changjun，JI Xiangyang.Research on compressed sensing ［J］.Journal of Computers，2011，34（3）：425－434 （in Chinese）.［戴琼海，付长军，季向阳.压缩感知研究 ［J］.计算机学报，2011，34 （3）：425－434.］

［4］FANG Hong，YANG Hairong.Greedy algorithms and compressed sensing ［J］.Acta Automatica Sinica，2011，37 （12）：1413－1421 （in Chinese）.［方红，杨海蓉.贪婪算法与压缩感知理论 ［J］.自动化学报，2011，37 （12）：1413－1421.］

［5］Candes E J.The restricted isometry property and its implications for compressed sensing ［J］.Comptes Rendus Mathematique，2008，346 （9）：589－592.

［6］Wu R，Huang W，Chen D R.The exact support recovery of sparse signals with noise via orthogonal matching pursuit［J］.Signal Processing Letters，IEEE，2013，20 （4）：403－406.

［7］SHEN Y，LI S.Sparse signals recovery from noisy measurements by orthogonal matching pursuit ［J］.arXiv Preprint arXiv：1105.6177，2011.

［8］Ding J，Chen L，Gu Y.Perturbation analysis of orthogonal matching pursuit ［J］.IEEE Transactions on Signal Processing，2013，61 （2）：398－410.

［9］Needell D，Vershynin R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit［J］.Foundations of Computational Mathematics，2009，9 （3）：317－334.

［10］Needell D，Tropp J A.CoSaMP：Iterative signal recovery from incomplete and inaccurate samples ［J］.Applied and Computational Harmonic Analysis，2009，26 （3）：301－321.

［11］Dai W，Milenkovic O.Subspace pursuit for compressive sensing signal reconstruction ［J］.IEEE Transactions on Information Theory，2009，55 （5）：2230－2249.

［12］MO Q，SHEN Y.A remark on the restricted isometry property in orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2012，58 （6）：3654－3656.