320t鱼雷罐铁水温降的有限元计算

马学东，蒋全强，马 硕，刘 莹，张艳兵

(1．辽宁科技大学 机械与自动化学院，辽宁 鞍山114051;2．上海交通大学 材料科学与工程学院，上海200240)

对于炼铁而言，为弥补铁水运输中过大的铁水温降，需提高铁水的初始温度，这不仅会加大炼铁时焦碳和喷煤的消耗，也会增加高炉废弃的气固液的排放．对于铁水运输而言，过大的铁水温降会造成鱼雷罐的结壳结瘤，降低罐体使用寿命;此外为了铁水保温还需增加烘罐的次数及增大烘罐时煤气的消耗，进而增加烘烤器的废气排放．对于炼钢而言，铁水温降越大，入炉铁水温度也随之降低，将影响转炉的废钢加入量，影响炼钢的吹氧作业．因此，减少铁水温降既是炼钢工艺、铁水运输工艺的要求，也是降低炼铁、炼钢能耗的要求［1，2］．同时也是钢铁业的节能降耗和节能减排的要求．

近年来，有关学者对混铁车罐体的热量损失及所造成的铁水温降研究作了大量的工作，取得了一定的成就［3～5］．但铁水温降计算都是采用间接方式进行，即首先计算罐体的热损失，然后依据能量守恒计算铁水温降，计算过程及方式较为复杂，温降效果不直观．且大多采用稳态传热计算，未能充分考虑时间因素及运输工艺的影响．同时，许多文献提出了罐口加盖及增设保温层等措施，但保温效果、铁水温降仍然缺乏精细化研究及计算方法支持．

本文以某炼铁总厂的320 t 鱼雷罐为研究对象，构建辐射矩阵来反映铁水和罐衬之间的传热，建立了包含铁水的二维轴对称铁水温降模型，采用有限元手段计算了320 t 鱼雷罐采取保温措施前后在储运铁水过程中的铁水温降．其计算方法新颖，计算结果直观．所做工作将为铁水保温措施的实施及铁水保温量化提供理论支持．

1 鱼雷罐热损失分析及运输工艺

1.1 鱼雷罐热损失分析

鱼雷罐在运输铁水时，按装有铁水与否分成空罐和重罐(装有铁水)两种罐况，铁水温降主要体现在重罐时，但空罐的蓄热状况对重罐时铁水温降也有较大的影响．

重罐时热量散失主要由以下几部分组成:①罐壳外表面以辐射和自然对流方式向外部空间散失热量;②耐火材料和罐壳的温度升高，即材料蓄热造成热损失;③不加盖时，渣层和罐衬内壁通过罐口向外部空间热辐射形成热损失［6］．以上①至③项的热损失都是时间的函数，时间越长，热损失越大，铁水温降越显著．此外热损失和铁水温降还与空罐时散热状况及空罐温度场有关．

1.2 实际运输工艺

根据某炼铁总厂的320 t 鱼雷罐铁水运输的实际工况，鱼雷罐首先在高炉进行受铁，铁水出高炉时温度约为1 500 ℃，受铁结束时铁水温度约为1 450 ℃．鱼雷罐受铁结束后，混铁车将铁水由炼铁厂运至炼钢厂，过3 h 后，将罐内的铁水倒入铁水罐，并在铁水罐内进行脱硫作业．即重罐时间为3 h．铁水倾倒结束后，鱼雷罐需空罐等待6 h后才能再次返回炼铁厂受铁．

2 热场分析

2.1 有限元模型

所分析的鱼雷罐几何尺寸及罐衬的布置来源于某炼铁总厂实际车型，该罐体的圆柱段直径为3.6 m，罐体总长为14.3 m(不含耳轴长度)，罐口直径1.65 m．鱼雷罐是关于两个平面对称的罐体，为了减少计算量，在进行有限元分析时，取其二维轴对称平面模型的1/4 为研究对象，几何模型如图1所示．采用二维轴对称平面单元Plane55，利用ANSYS 软件智能网格器进行网格划分，网格划分后有限元模型如图2所示．

2.2 热边界条件

有限元模型包含铁水，罐体与铁水之间的传热通过辐射矩阵来实现，并充分考虑罐壳外表面的散热．

图1 鱼雷罐几何模型Fig.1 Geometry model of torpedo ladle

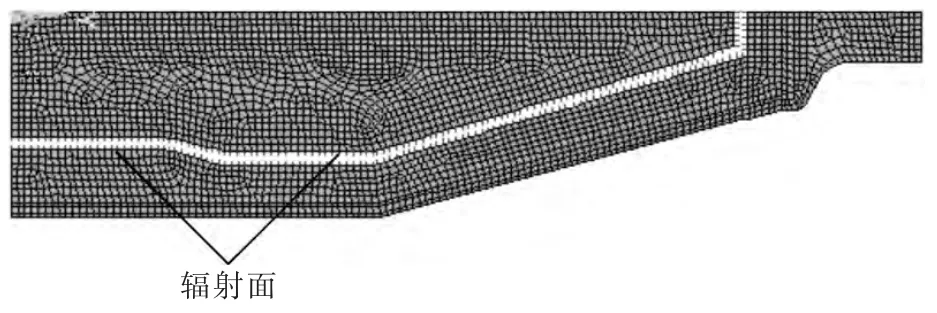
图2 鱼雷罐有限元模型Fig.2 Finite element model of torpedo ladle

2.2.1 罐壳外表面的边界条件

罐壳最外层受到自然对流和辐射换热的影响，在罐壳的表面加载综合对流换热系数hc，该系数考虑了自然对流和辐射换热的综合换热效应，且该系数是罐壳外表面温度的函数．其具体数值见有关文献［7］．

2.2.2 铁水与罐衬内表面的边界条件

重罐时，铁水与罐衬内壁直接接触，热量传递方式通过热辐射和热对流进行，因铁水温度很高，传热主要以热辐射方式进行，故让铁水和罐衬离开很小的间隙，在此间隙之间构建辐射矩阵，来反映铁水与罐衬之间的辐射换热，且根据有关文献，也考虑对流换热量，根据热量守恒，适当扩大发射率来计入对流换热份额［8］．

2.2.3 罐口的热辐射

重罐时，铁水上部的渣层和上部空腔壁面通过罐口向外界进行热辐射，受限于二维轴对称模型，该辐射量在模型中反映不出来，这部分热损失及造成的铁水温降将另行计算．

2.3 模拟参数及载荷步设置

热场瞬态模拟时，材料参数和载荷步的设置必不可少．

2.3.1 材料参数

铁水、罐衬、罐壳的比热容、导热系数、发射率等具体数据来源于有关手册及论文［9，10］．但铁水的比热容，铁水和罐衬之间的发射率等受装入量的影响，需作调整．

(1)铁水比热容的调整

铁水装入量影响换热量，而二维轴对称模型是在假设装满情况下进行的，为了保证铁水真实的温降值，须根据热量守恒来调整模型中的铁水比热容的赋值，具体步骤如下:

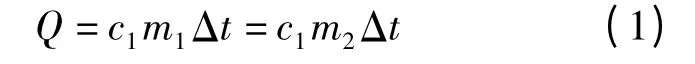
式中:Q 为铁水热量，J;c1，c2为实际及模型中的铁水比热容，J/(kg·℃);m1，m2为实际及模型中的铁水质量，kg;Δt 为实际铁水温降，℃．

由式(1)推出:

因此，在模型中须将比热容按式(2)赋值．

(2)发射率的调整

铁水装入量、装入深度影响换热量，即铁水同罐壁的接触面积影响换热量，而二维轴对称模型是在假设铁水同罐壁全接触条件下构建的，因此，须根据热功率守恒来调整模型中的发射率的赋值，具体步骤如下:

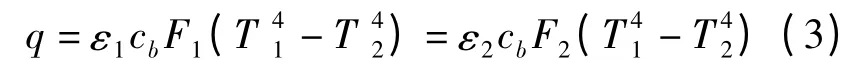
式中:q 真实热量，W;cb为黑体辐射系数5.67 ×10－8W/(m2·K4);ε1，ε2为实际及模型中发射率;F1，F2为实际及模型中的铁水同罐壁的接触面积，m2;T1，T2为实际温度，K．

由式(3)推出:

因此，在模型中，须将发射率按式(4)调整．

2.3.2 载荷步

(1)初始温度场(初始载荷步)

考虑鱼雷罐烘罐处理及热惯性的影响，以及现场提供的数据，空罐结束时罐衬内壁的温度大约在900 ℃左右，故在罐衬内壁上施加的温度为900 ℃，罐壳外表面施加综合对流换热系数hc，求解得出非均匀分布的温度场，此温度场为瞬态分析时初始温度场．

(2)瞬态载荷步

瞬态分析时间来源于现场实际，重罐时间为2～4 h，取平均值为3h．故瞬态时间设定为3 h，在代表铁水的面积上施加铁水入罐的初始温度为1 450 ℃，罐壳外表面加入综合对流换热系数hc，写瞬态载荷步．

2.4 有限元结果

经求解，得到3h 时的整体温度场云图，铁水温度云图及铁水特征点A、B、C 三点的时间温度历程图，如图3 至图5所示．

由图3 和图4 可知，铁水中部温度较高，为1 397～1 440 ℃，靠近罐衬圆锥段的角部铁水温度最低，为1 046 ℃，选择代表铁水的单元，对这些单元温度求和及取平均，得到铁水的平均温度值为1 355 ℃，故铁水温降为1 450 ℃－1 355 ℃=95 ℃．由于模型的限制，此温降相当于加盖时铁水温降．

图3 3 h 时整体温度(℃)场云图Fig.3 The whole temperature distribution in 3 h

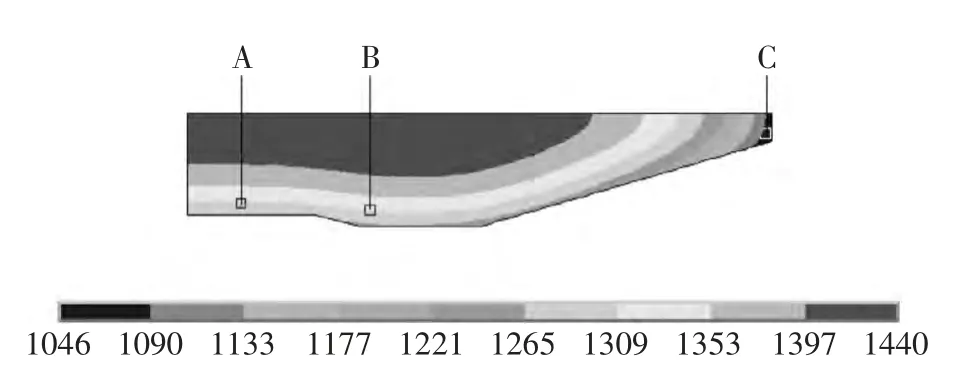
图4 3 h 时铁水温度(℃)场云图Fig.4 Temperature distribution of molten iron in 3 h

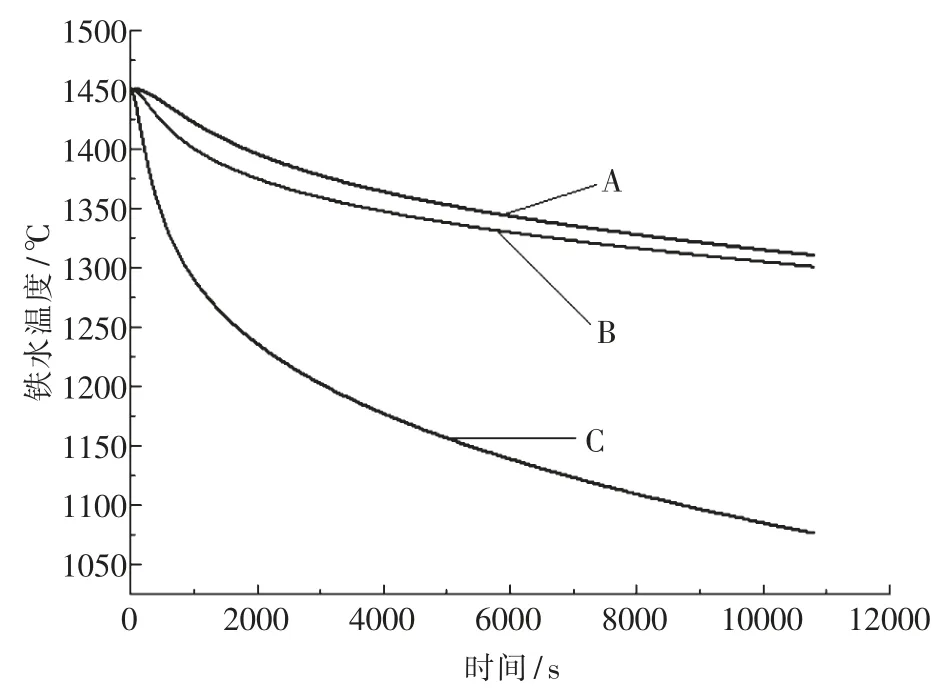
图5 特征点时间温度历程曲线Fig.5 Time-temperature curve of the feature points

由图5 可知，靠近罐衬圆柱段的A 点在3 h内铁水温度由1 450 ℃下降到1 310 ℃，铁水温降为140 ℃．B 点下降到1 300 ℃，铁水温降为150 ℃．靠近罐衬圆锥段角部C 点，在3 h 内铁水温度由1 450 ℃下降到1 075 ℃，铁水温降为375 ℃．

3 罐口热损失及铁水温降

3.1 罐口热辐射及造成的铁水温降

当罐口敞开时，鱼雷罐上部为空腔，铁水上部为渣层．渣层、上部内壁、罐口组成一个相互辐射的系统，但轴对称二维模型并不能反映这种工况．通过空腔法［11］按式(5)计算这部分辐射的热量，其中渣层温度取为平均温度，取值来源于现场，为1 100 ℃．

内壁通过罐口向外散失热量Q1为:

其中:

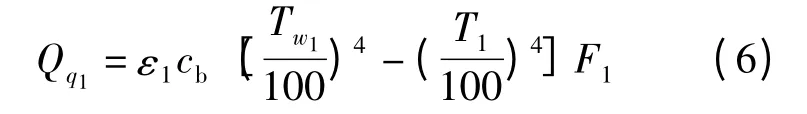
式中:Qq1为通过罐口向外界辐射的热流量，W;为空罐时间，s;ε1为渣的发射率;为渣层的热力学温度，K;T1为外部环境的热力学温度，K;F1为罐口面积，m2．

经计算得:

Q1=2．88 GJ

根据热能守恒定律，将罐口热辐射损失折算铁水温降为:

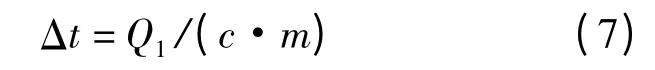
式中:m 为铁水质量，kg;c 为铁水比热容，J/(kg·℃);Δt 为铁水温降，℃．

其中根据实际320 t 鱼雷罐实际运行情况，其铁水装入量为260 t/次．

解得:

Δt=15 ℃

3.2 总铁水温降

采用轴对称模型计算出的铁水温降为95 ℃，罐口热辐射造成的铁水温降为15 ℃．总铁水温降为110 ℃，根据现场数据，现场实际铁水温降为120 ℃，误差为8.3%，因此，计算数据接近于工程实际．

4 保温状态下的铁水温降

以上计算是在鱼雷罐未设保温层时进行的，增设保温层下铁水温降尚无人进行精确的计算．但保温层设置后须重建热分析模型．

4.1 保温层设置原则

增设保温层的厚度为h1，原永久层的厚度为h，那么，增设保温层后，永久层的厚度变为h2=h－h1，即增设保温层后，罐衬的总厚度不变，因而罐容不变．

4.2 边界条件

保温层采用硅酸镁隔热板，其材料参数见表1．重新建立模型，划分网格，然后，施加边界条件．

4.2.1 初始温度场

考虑鱼雷罐烘罐处理及热惯性的影响，经反复试算，得出加入保温层后，未装铁水时，即重罐刚刚开始时，罐衬内壁的温度大约在950 ℃左右，加入边界条件，求解得出空罐时的稳态温度场，把此温度场作为初始温度场．

4.2.2 瞬态载荷步

瞬态时间设为3 h，同时构建辐射矩阵来反映铁水同罐衬的热交换．然后参照原始罐型的加载方式，施加边界条件．参照原始罐形载荷步的写入，写重罐时瞬态载荷步．

4.3 保温后结果

通过运算后得到增设保温层后铁水的温度场云图，如图6所示．

图6 3 h 时保温罐型温度(℃)场云图Fig.6 Temperature distribution of insulation tank in 3 h

由图6 可知铁水中部温度较高，为1 404～1 440 ℃，靠近罐衬圆锥段的角部铁水温度最低，为1 116 ℃．选择代表铁水的单元，对这些单元温度求和及取平均值，得到铁水的平均温度值为1 367 ℃;故铁水温降为1 450 ℃－1 367 ℃=83 ℃．由前计算可知，不加盖时造成的铁水温降为15 ℃．因此，总铁水温降为98 ℃．

5 结 论

(1)以传热学理论为基础，以热量守恒及热功率守恒为依据，采用辐射矩阵描述铁水和罐衬的传热，在此基础上建立了包含铁水的二维轴对称热分析模型，较为真实和直观地描述了铁水的非均匀温度场，所用方法较为新颖．

(2)计算结果表明:现有的鱼雷罐在储运时会产生110 ℃铁水温降，同实际温降120 ℃的误差为8.3%，表明计算是可行的，计算可满足工程需要．

(3)计算结果表明:加盖时，铁水温降较现有鱼雷罐可减小15 ℃，加盖和增设保温层后，铁水温降较现有鱼雷罐可减小27 ℃．

［1］Kaufman D J，Shockley L W．Torpedo car refractories and scheduling improvement sat ACME steel［C］．Steelmaking Conference Proceedings，1994，77(15)，571－573．

［2］徐大勇，刘常鹏，杨大正，等．铁水温度价值的分析和评价［J］．冶金能源，2007，26(3):7－10．

(Xu Dayong，Liu Changpeng，Yang Dazheng，et al．Analysis and evaluation of temperature value about molten iron［J］．Energy for Metallurgical Industry，2007，26(3):7－10．)

［3］吴懋林，张永宏，杨圣发，等．鱼雷罐铁水温降分析［J］．钢铁，2002，37(4):12－16．

(Wu Maolin，Zhang Yonghong，Yang Shengfa，et al．Analysis of hot metal temperature drop in torpedo car［J］．Iron and Steel，2002，37(4):12－16．)

［4］荣军，姜华，宋利明，等．宝钢混铁车保温改造效果评估算法［J］．材料与冶金学报，2006，5(2):90－93．

(Rong Jun，Jiang Hua，Song Liming，et al．Effect evaluation algorithm of heat preservation improvement for torpedo car in baosteel［J］．Journal of Materials and Metallurgy，2006，5(2):90－93．)

［5］向顺华，周仁义，刘铁树，等．宝钢铁水输送过程中温度预报传热模型的研究［J］．冶金自动化，2002，26(2):23－25．

(Xiang Shunhua，Zhou Renyi，Liu Tieshu，et al．The study of heat transfer model for temperature estimation during netal transporting in baosteel［J］．Metallurgical Industry Automation，2002，26(2):23－25．)

［6］刘诗薇，于景坤，颜正国，等．鱼雷罐车热量损失的影响因素及控制方法［J］．材料与冶金学报，2010，09(3):159－162．

(Liu Shiwei，Yu Jingkun，Yan Zhenguo，et al．Factors and controlm ethods of the heat loss of torpedo－ladle［J］．Journal of Materials and Metallurgy，2010，09(3):159－162．)

［7］任泽霈，梅飞鸣．传热学［M］．北京:中国建筑工业出版社，1993．

(Ren Zepei，Mei Feiming．Heat transfer［M］．BeiJing:China Architecture Building Press，1993．)

［8］于学斌，朱志强，时启龙，等．320 t 鱼雷罐内铁水流场的物理模拟［J］．河南冶金，2006，09(14):37－40．

(Yu Xuebin，Zhu Zhiqiang，Shi Qilong，et al．Physical simulation of hot metal flow field in 320 t torpedo［J］．Henan Metallurgy，2006，09(14):37－40．)

［9］余其铮．辐射换热原理［M］．哈尔滨:哈尔滨工业大学出版社，2000．

(Yu Qizheng．Radiation heat transfer principles［M］．Harbin:Harbin Institute of Technology Press，2000．)

［10］杨贤荣．辐射换热角系数手册［M］．北京:国防工业出版社，1982．

(Yang Xianrong．Angle of radiation heat transfer coefficient of the manual［M］．Beijing:National Defense Industry Press，1982．)

［11］卞伯绘．辐射换热的分析与设计［M］．北京:清华大学出版社，1988，10．

(Bian Bohui．Radiative heat transfer analysis and design［M］．Beijing:Tsinghua University Press，1988，10．)