基于本底趋势线模型预测的某型火箭炮PID调平系统
2015-12-23邢立新,沈中卿
【装备理论与装备技术】
基于本底趋势线模型预测的某型火箭炮PID调平系统
邢立新,沈中卿
(陆军军官学院,合肥230031)
摘要:为了解决某型火箭炮手动调平过程中存在调平时间过长、精度不高的问题,提出了基于PID控制的自动调平系统,并且运用本底趋势线预测模型对传统PID模型进行了改进,减少因滤波与数据预测而导致信息延时的误差。仿真实验表明,改进后的PID控制算法,更加符合系统的实际调平过程,系统的调平精度也得到了提高。
关键词:PID控制;Butterworth滤波,本底趋势线预测模型
收稿日期:2015-05-06
作者简介:邢立新(1964—),男,硕士,教授,主要从事炮兵射击研究。
doi:10.11809/scbgxb2015.09.001
中图分类号:TJ393
文章编号:1006-0707(2015)09-0001-04
本文引用格式:邢立新,沈中卿.基于本底趋势线模型预测的某型火箭炮PID调平系统[J].四川兵工学报,2015(9):1-4.
Citation format:XING Li-xin, SHEN Zhong-qing.Research on PID Leveling System of A Rocket Launcher Based on Background Trend Line Prediction Model[J].Journal of Sichuan Ordnance,2015(9):1-4.
Research on PID Leveling System of A Rocket Launcher
Based on Background Trend Line Prediction Model
XING Li-xin, SHEN Zhong-qing
(Army Officer Academy, Hefei 230031, China)
Abstract:For solving the problem of long leveling time and low leveling accuracy generated in the process of artificial leveling, the automatic leveling system based on traditional PID (Proportion Integration Differentiation) was proposed, and by introducing background trend line prediction model (BTLPM) into the traditional PID model, the error of information lag caused in the process of filtering and data predicting was deduced greatly. The simulation result of MATLAB show that compared with the accuracy of traditional PID model, the one of improved PID model which meets actual leveling process better is higher.
Key words: PID control; Butterworth filtering; background trend line prediction model
瞄准系统是火箭炮的“眼睛”,其状态的好坏直接影响火箭炮能否“打得准”,每次设计前必须对每门火箭炮的瞄准系统进行多项技术检查,检查合格后方可进行射击,而这些技术检查项目大部分都是在火箭炮处于水平情况下进行的,因此火箭炮的水平精度是决定检查结果的关键。
目前用于火箭炮调平的主要方法为人工调平,但是由于人工因素的参与,调平结果存在调平精度不高和调平速度不快的缺点。而运用于其他武器装备(雷达、导弹发射车等)的调平系统大多都是传统的PID模型,不考虑因滤波和信息滞后带来的误差,势必会影响调平系统的精度[1-3]。
本研究总金额针对理想情况下PID模型中存在的信息滞后问题,引入Butterworth滤波和本底趋势线模型,对支撑腿原始上升高度数据进行滤波、预测后代入改进后的PID模型,并与传统PID模型进行比较。
1系统构成
调平系统采用的是四点式液压调平系统,即调平系统的支撑机构为四点支撑腿式,伺服系统为液压式,调平系统自动化程度属于全自动化,系统的构成图如图1所示。
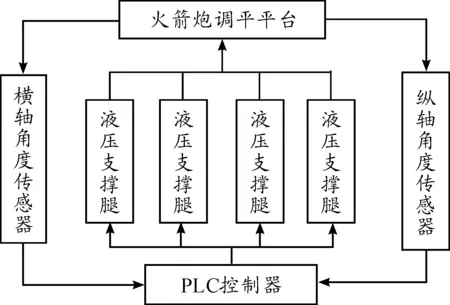
图1 调平系统构成示意图
2液压支撑腿数学模型
液压系统作为调平系统的被控对象,其内部的传递函数只与系统的结构有关,与系统输入无关。而且4个液压支撑腿的数学模型及分析过程均一样,为了研究的方便,这里就以一个支撑腿为研究对象。
1) 滑阀流量方程
滑阀流量方程描述的是阀芯产生的位移与流入缸内流量之间的关系
(1)
其中:q是流入缸体的流量;Cd是流量系数;ω为阀口的面积梯度;kx是电流和阀芯位移之间的比例系数;δ为阀口的遮盖量;p是系统和负载的压力差;ρ为液压油密度;I输送给液压系统的电流。
2) 柱塞缸流量连续方程
(2)
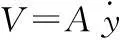
(3)
其中:Cep为泄漏系数;pL为柱塞缸负载压力;V为柱塞缸腔内的体积;βe为有效体积弹性模数;A为柱塞缸活塞杆的面积;y为活塞杆的位移也是负载上升的高度。
3) 力平衡方程
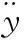
(4)
其中:m代表负载与活塞的总质量折算成活塞上的质量;BP代表负载及活塞的黏性阻尼系数;k是负载的弹性系数。
联立式(1)、式(2)、式(3)与式(4)并进行拉式变换,可以得出被控对象的传递函数为:
(5)
3理想情况下的PID模型
PID控制作为控制领域的重要理论,已经具有百年历史,其实质就是将偏差的比例、积分和微分单元通过线性组合构成控制量对被控对象进行控制。数字PID数学模型为
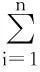
Kd[e0(n)-e0(n-1)]/T
(6)
其中:e0(n)=Yd(n)-Y0(n),为第n个时刻的系统采样值与模型的输出值之间的偏差;T为系统的采样周期;Kp,Ki,Kd分别为PID模型的比例、积分与微分系数;I(n)为滑阀的输入电流。所以理想情况下PID的系统原理图如图2所示。

图2 理想情况下PID的系统原理框图
假设某型火箭炮为40 t,系统采用的角度传感器的采样周期为0.1s,其主要参数为:柱塞缸的面积的A为0.025 m2,流量系数Cd为0.7,阀口的面积梯度ω为0.04 m,比例方向阀的阀口开度kx为0.2,液压油的密度ρ为870 kg/m3,因为调平系统的质量相对与火箭炮的质量来说很小,可忽略不计,所以m=40 000/4=10 000 kg,塞杆的行程为L=0.19 m,所以柱塞缸的容积为V=AL=0.004 75 m3,系统体积弹性模量βe为700 MPa,泄漏系数Cep为1×10-12m5/(N·s)。Bp,k因为很小可以忽略不计。因此系统的传递函数式(5)代入数据可化简为
(7)
根据PID参数试凑法可得Kp=25,Ki=0.8,Kd=10.2,且经过Matlab仿真可知,理想情况下的支撑腿的上升高度随时间的变化曲线图如图3(a)所示。但是实际的液压支腿上升曲线却如图3(b)所示,导致实际曲线图发生改变的原因有2个,一是液压支腿在上升过程中的震动现象会使角度传感器测得的角度信号产生摆动;二是角度传感器测得的角度信号与液压千斤顶应上升的高度信号之间的时间差。
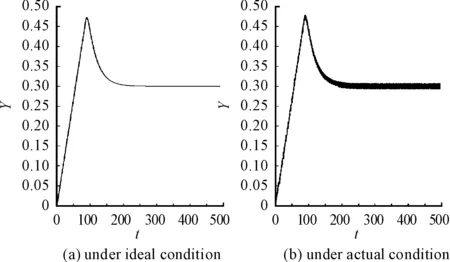
图3 支撑腿上升高度曲线
因此实际用到的PID模型为
(8)
4改进后的PID模型
上面所描述的2种情况都会给PID控制带来较大的误差,首先传感器的摆动使得PLC控制器误将上升信号当作调平系统的实际高度信号。针对这种情况,提出先对摆动信号进行滤波;其次延时信号的运用也会给PLC的控制带来干扰,尤其在调平系统已经达到水平状态的时候,系统会错误的以为火箭炮还处于未水平状态而继续调整。针对这种情况,提出本底趋势线模型对支撑腿的上升高度今次那个实时预测。
4.1Butterworth滤波传递函数
滤除上升曲线中的高频摆动信号需要对上升信号进行低通滤波,而目前常用于低通滤波的有Chebyshev滤波和Butterworth滤波。因为Butterworth滤波在时域和频域上都具有很好的性能,而且容易实现、稳定性好,所以常用于控制与通信领域[4,5]。
Butterworth幅度的平方函数如式(9)所示,且幅频特性随阶次n的变化曲线图如图4所示。
(9)
式中:n为滤波器的阶次;ωc为滤波器的截止频率。
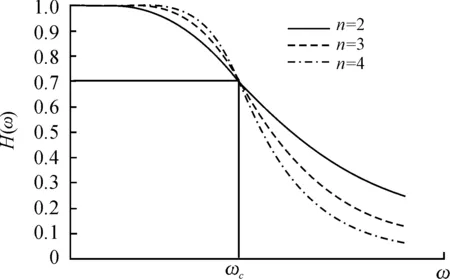
图4 Butterworth 幅频特性随阶次n的变化曲线
(10)
经归一化处理后可得
(11)
令式(11)的分母为0,即1+(-s2)n=0,则式(11)得极点为
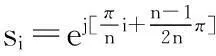
(12)
(13)
由式(12)可知,所有的极点都是均匀并且共轭的,而且根据系统稳定的充要条件:系统的特征方程所有的极点全部具有负实部。所以有
(14)
通过Matlab计算,可知当输入阶跃信号时,随着Butterworth阶次的增加,系统的超调量和调节时间明显增加,具体如表1所示。

表1 Butterworth 传递函数性能
对于支撑腿的实际高度信息和摆动信号来说,其频率相差较大,简单的2阶传递函数就可以满足要求,所以火箭炮的调平系统选用2阶传递函数H(s)
(15)
4.2本底趋势线模型
本地趋势线模型的实质是对已知的时间序列进行3种模型的拟合,将拟合函数得出的时间序列与原时间序列进行相关性计算,依据计算结果选用相关性最大的函数作为本地趋势线模型,然后就可以预测后面任意时刻的时间序列。
常用的时间序列有以下3种:
直线-逻辑增长复合模型,方程为

(16)
直线-三角函数复合模型,方程为
Y=at+b+csin(ωt+θ)
(17)
指数-三角函数复合模型,方程为
Y=a·ebt+csin(ωt+θ)
(18)
其中,a,b,c,d,K,θ,ω是模型参数,可以通过将时间序列代入上面的方程计算求得。
就近选取个n传感器监测时间点构成时间组T={t1,t2,…,tn}和支撑腿高度原始时间序列Y0={y0(1),y0(2),…,y0(n)}。分别用3种模型对原时间序列进行拟合得出3种趋势函数,代入时间组T可以求得3个时间序列Yi={yi(1),yi(2),…,yi(n)},i=1,2,3,i时间序列的编号。计算3个时间序列与原时间序列的相关性
i=1,2,3
(19)
选取最大相关性模型作为本底趋势线预测模型,进而预测第n时刻Δt后的支撑腿高度Y1(n+Δt),Δt是因为滤波和预测所导致的支撑腿信息延时部分。
4.3基于预测的PID控制
依据本底趋势线模型求得k+Δt时刻的支撑腿高度Y1(n+Δt),就可以计算偏差信息
e1(n+Δt)=Yd(n+Δt)-Y1(n+Δt)
(20)
将式(20)代入式(6),可得改进后的PID模型为
e1(n+Δt)Δt)+Kd[e1(n+Δt)-e1(n)]/Δt
(21)
改进后的PID系统原理图如图5所示。
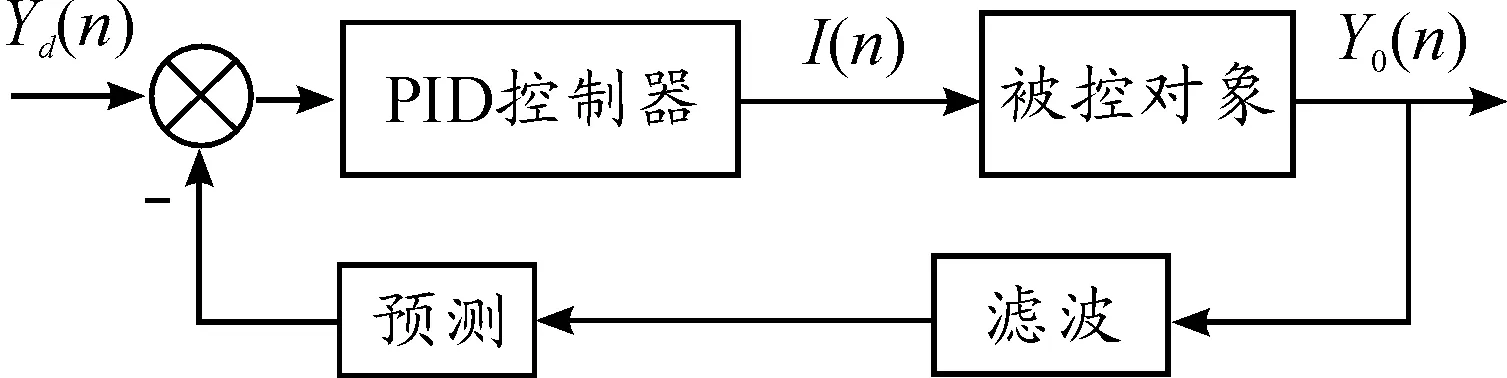
图5 改进后的 PID系统原理
5仿真实验
令n=8.通过Matlab计算,滤波和高度与角度的转化时间之和Δt=0.25s.则改进后的PID模型与传统PID模型控制稳定后的比较图如图6所示。由图6可知改进后的PID模型的调平精度要好于传统PID模型。
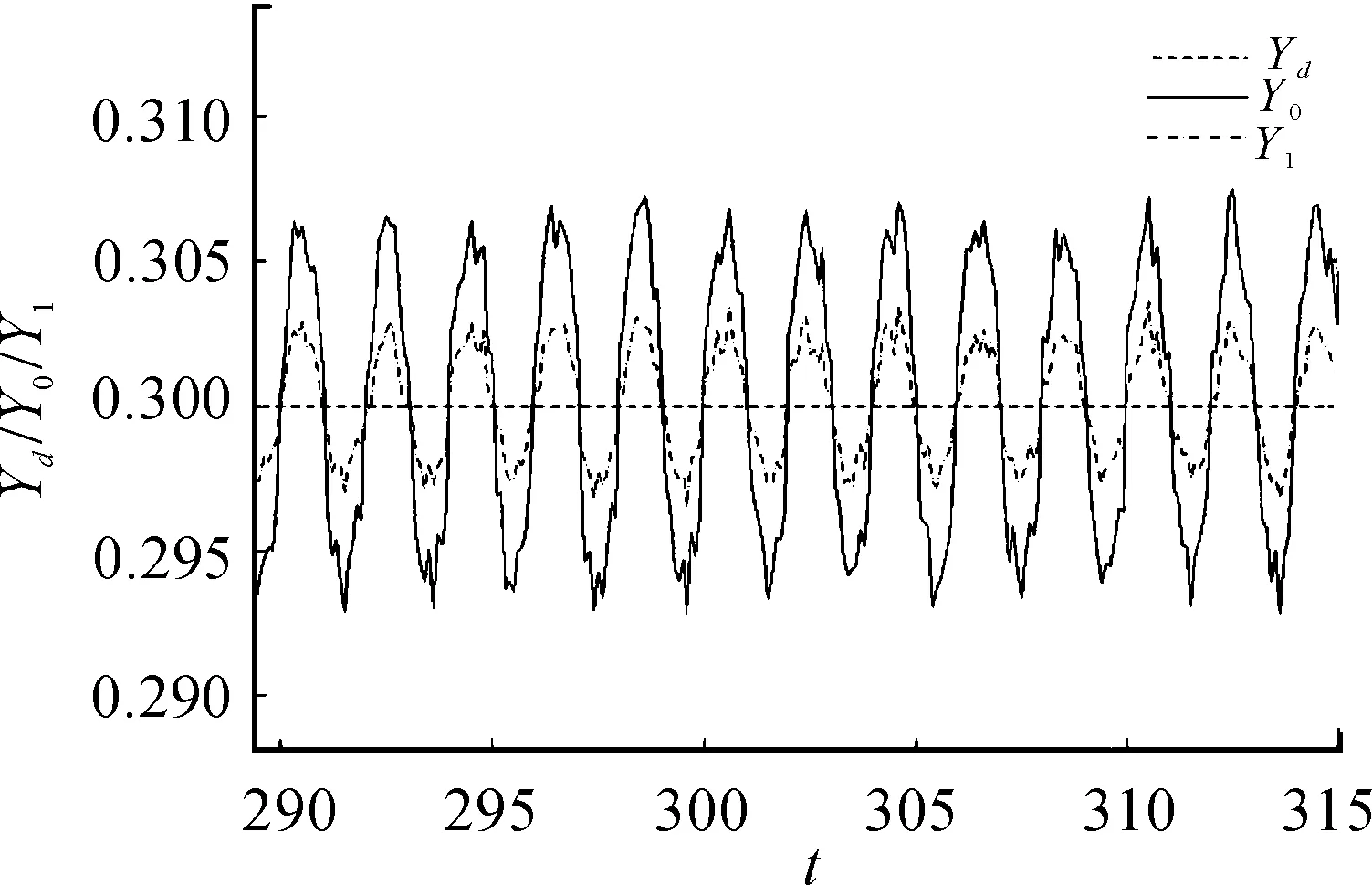
图6 调平稳定后改进前后的 PID模型
6结束语
基于传统PID模型的自动调平系统不仅使火箭炮实现自动技术保障,而且减少了操作人员的工作量。基于本底趋势线模型的PID调平系统则是在调平时间和调平精度上达到了更高的水准。而且该模型可以运用到其他武器装备(导弹发射车、雷达)的调平过程中,具有很好的推广价值。
参考文献:
[1]吴华强,战延谋.某型火箭炮车载辅助调平装置设计[J].舰船电子工程,2011(12):178-180.
[2]汪伟.重型车辆液压自动调平模糊PID控制研究[D].武汉:武汉理工大学,2009:28-29.
[3]王伟,张晶涛,柴天佑.PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355.
[4]李钟慎.高阶Butterworth低通滤波电路的快速设计[J].工业仪表与自动化装置,2007,30(12):16-19.
[5]王力,钱林方,高强,等.基于灰预测模糊PID的随动系统负载模拟器力矩控制研究[J].兵工学报,2012(11):1379-1386.
[6]邢立新,沈中卿.基于CMAC-模糊PID模型的火箭炮调平控制系统仿真[J].四川兵工学报,2015(8):1-4.
(责任编辑周江川)
