基于径向基函数神经网络的空间碎片撞击模式识别研究

杜 刚，何 朔，于海鹏

（中国运载火箭技术研究院 研发中心，北京 100076）

0 引言

随着人类空间活动的增加，各类航天器爆炸、碰撞解体、废弃物等产生的空间碎片日益增多[1]。当空间碎片与在轨航天器交会碰撞时，将对航天器的安全构成严重威胁。空间碎片对航天器的损伤主要体现为动能损伤，属于超高速碰撞的范畴，碰撞所产生的冲击力远大于航天器结构材料的强度，造成的破坏是严重的甚至是致命的[2]。

目前对于尺寸＜10 cm 的空间碎片难以监测和跟踪；对于尺寸＜1 cm 的空间碎片，航天器只能通过防护结构来尽量减轻碎片撞击造成的损伤[3]。

既然撞击不可规避，人们在防护措施的基础上正研究一种在轨感知系统，试图随时了解航天器空间碎片撞击损伤的情况[4]。目前，声发射方法受到广泛关注，既能实现大范围实时监测，又对使用环境要求不高[5]。

本文利用径向基函数神经网络对大量的仿真试验样本数据进行训练，拟利用训练完成的神经网络对撞击信号进行分析，反演获取碰撞参数。

1 径向基函数神经网络基本原理

径向基函数（radial basis function,RBF）神经网络是单隐层的前向网络[6]，它由输入层、隐层和输出层三层构成，其结构如图1所示。

输入层节点将信号输入到隐层节点，隐层节点的基函数对输入数据在局部产生响应：当输入信号靠近基函数的中央范围时，隐层节点将产生较大的输出；当输入信号远离基函数中心时，隐层节点的输出减小。由此可以看出，在RBF 神经网络中，仅当输入信号落在输入空间中一个很小的指定区域时，隐层节点才作出有意义的非零响应，故RBF神经网络又被称为局部感知场网络。

最常用的基函数是高斯函数：

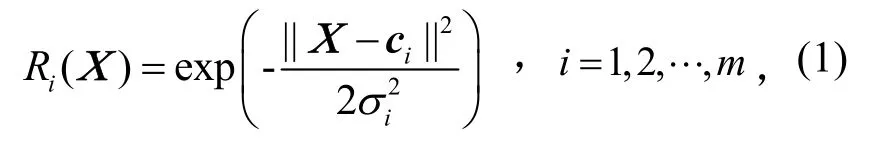
其中：X是n维输入向量；ci是第i个基函数的中心，与X具有相同维数的向量；σi为第i个中心向量的半径，它决定了该基函数围绕中心点的宽度；Ri(X)为第i个隐层节点的输出，Ri(X)在ci处有一个唯一的最大值；||X-ci||表示X和ci之间的距离，随着||X-ci||的增大，Ri(X)迅速衰减到0。

RBF神经网络的输出是Ri(X)到yi的线性映射，即

其中Wi为输出层权值，i= 1,2,···,m。

下面分析中以声发射信号的幅值、能量、持续时间、撞击观测点等作RBF 神经网络的输入向量，以撞击速度作为输出向量，形成多维向量到单一变量的映射。

2 高速撞击数值模拟实验与数据分析

2.1 仿真参数及损伤结果

采用AUTODYN 显式非线性动力分析软件进行仿真。以板厚方向为x、板的高度为y建立二维模型。板厚5 mm，弹丸直径3.2 mm，材料均为铝，撞击速度方向垂直于板，速度大小从1.0 km/s 到 5.6 km/s 不等。图2为仿真的两种撞击损伤结果（未穿透和穿透）。

图2 仿真的撞击损伤结果 Fig.2 The simulation results of space debris impact damage

2.2 信号特征参数提取

由于声发射传感器响应的是质点运动速度，故仿真计算后得到的是板上不同位置处的质点运动速度。图3为v=1 km/s 速度撞击时在y=9.9 mm 处的波形及其频谱，下面以该波形为例，详细描述声发射撞击信号特征参数提取过程。从波形频谱中可以看出信号中含有强烈的低频信号，这是由撞击后板的振动引起的，其中含有撞击后产生的缺陷信息，但不容易被分析。因此，先采用小波降噪[7]的方法消除振动和反射波，然后选择能量最为集中的滤波频率800～1100 kHz，滤波后结果如图4所示，其时频图如图5所示。从时频图可以看出提取出的信号在时间和频率上能量均比较集中。

图3 撞击速度v=1 km/s 时在y=9.9 mm 撞击观测点处的 波形及其频谱 Fig.3 The waveform and spectrum for v = 1 km/s at y = 9.9 mm

图4 经800～1100 kHz 滤波后的波形及其频谱 Fig.4 The waveform and spectrum after filtration through 800～1100 kHz

图5 经800～1100 kHz 滤波后的时间-频率图 Fig.5 The time-frequency diagram after filtration through 800～1100 kHz

2.3 信号特征与撞击速度之间的关系

在信号滤波后提取信号幅值特征时，发现信号幅值、能量、持续时间等特征参数与撞击速度之间存在一定的映射关系，典型如图6所示。其他特征参数与撞击速度也存在单调映射关系，为节省篇幅，在此不再赘述。

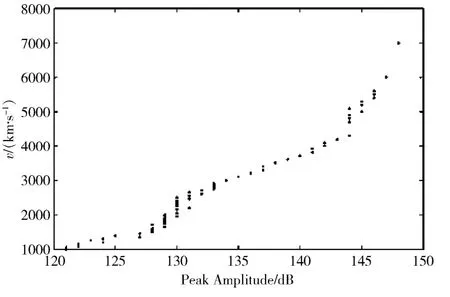
图6 信号幅值与撞击速度之间映射关系（频率范围 800～1100 kHz） Fig.6 The relationship between the signal amplitude and the impact velocity (with signal frequency between 800～1100 kHz)

3 用RBF 神经网络进行反演计算

3.1 特征向量提取、训练及反演计算结果

从仿真数据中随机提取100 个碰撞产生的声发射信号，分别提取出上述特征参数，构建成100组的特征向量，以撞击速度作为输出，建立RBF神经网络并对其进行训练。将另外100 组未参与训练的声发射信号提取特征向量后，输入到训练好的RBF 神经网络，反演计算撞击速度。统计反演的撞击速度与仿真的撞击速度间的相对偏差，结果如 图7所示。反演计算得到的撞击速度与仿真的撞击速度间的平均相对偏差为7.7%，相对偏差在10%以内的比例为74.5%。

图7 反演速度的相对偏差分布 Fig.7 The relative error distribution of the inversion impact velocity

3.2 撞击观测点对反演识别正确率的影响

为进一步提高反演准确率，尝试缩小撞击观测点范围，发现随着撞击观测点范围的缩小（即撞击观测点距撞击处的距离越小），相对偏差就越小，具体结果如表1所示。

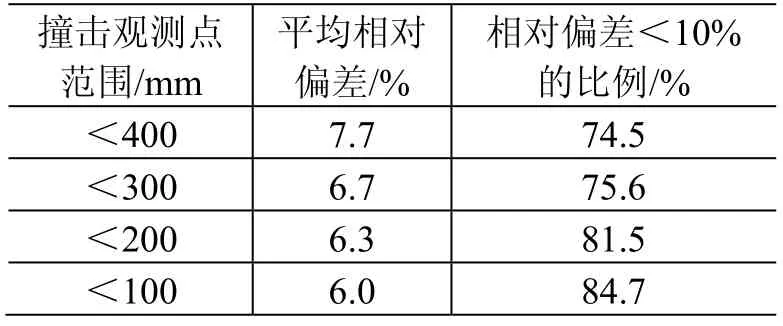
表1 撞击观测点范围与相对偏差关系 Table1 The relationship between the range of observation points and the relative error

出现上述情况的主要原因是随着观测点与撞击点距离的增大，信号衰减加剧，进而波形特征不明显，对识别产生影响。在本次数据处理过程中，仅采用了一种弹丸，其质量一定，根据仿真数据获知，当该弹丸的撞击速度达到2.15 km/s 以上时，可将板材完全穿透。因此，根据RBF 神经网络反演计算的速度，可判断出航天器外壁是否被碎片穿 透。经统计分析发现，识别正确率也与撞击观测点位置有关，即：撞击观测点与撞击点距离越近，则识别正确率越高；当撞击观测点与撞击点距离＜200 mm 时，对于穿透与否的识别正确率可以达到97.3%。

4 结束语

本文利用RBF 神经网络数值模拟对高速撞击产生的声发射信号进行模式识别，反演出弹丸撞击速度，得到如下结论：

1）频率为1 MHz 附近的高频声发射信号特征与弹丸撞击速度呈单调映射关系。

2）RBF 神经网络能够有效利用声发射信号特征反演弹丸撞击速度。

3）观测点与撞击位置的距离越近，反演和识别的准确率越高。这是因为距离越短，声信号的传播损失以及畸变的影响越小。但实际应用中不可能确定观测点与撞击位置之间的距离，因此可先对撞击位置精确定位，并采取补偿的方法减少信号衰减和畸变后，再进行识别分析。该方法有待进一步研究。

目前研究仅对撞击速度进行了反演，且仿真对象仅针对同一规格尺寸弹丸，其应用有一定的局限性。如何针对更多情况反演出更多信息，亦有待后续深入研究。

（References）

[1] 都亨.空间碎片[M].北京: 中国宇航出版社,2007: 1

[2] 李怡勇,沈怀荣,李智.空间碎片环境危害及其对策[J].导弹与航天运载技术,2008,298(6): 31-35 Li Yiyong,Shen Huairong,Li Zhi.Space debris' hazard and countermeasures[J].Missiles and Space Vehicles,2008,298(6): 31-35

[3] 龚自正,韩增尧,庞宝君.空间碎片防护研究现状与国内发展建议[J].航天器环境工程,2010,27(1): 34-41 Gong Zizheng,Han Zengyao,Pang Baojun.A review of studies on protection against M/OD[J].Spacecraft Environment Engineering,2010,27(1): 34-41

[4] IADC.Sensor systems to detect impacts on spacecraft,IADC-08-03[R],2013

[5] 唐欣.超高速撞击板波特性与声发射空间碎片在轨感知技术[D].哈尔滨: 哈尔滨工业大学,2008

[6] 王炜,吴耿锋,张博锋,等.径向基函数(RBF)神经网络及其应用[J].地震,2005,25(2): 19-25 Wang Wei,Wu Gengfeng,Zhang Bofeng,et al.Neural networks of radial basis function (RBF)and its application to earthquake prediction[J].Earthquake,2005,25(2): 19-25

[7] 李英,张淑贞,许康生.小波降噪方法在地震信号处理中的应用[J].西北地震学报,2006,28(2): 159-162 Li Ying,Zhang Shuzhen,Xu Kangsheng.Application of wavelet transfer in seismic signal denoise[J].Northwestern Seismological Journal,2006,28(2): 159-162