真空低温环境对摄影测量精度的影响

张博伦，杨林华，蒋山平，张鹏嵩

（北京卫星环境工程研究所，北京 100094）

0 引言

摄影测量凭借其测量速度快、非接触式测量、对测试环境要求低、精度高等优势在众多的测量方法中逐渐为航天领域科研人员所采用，常用于模拟空间环境下卫星天线面形的变形测量[1]等。摄影测量系统一般由相机、测量标尺和测控系统等组成[2]。摄影测量的精度影响因素包括常规的影响因素和特殊环境条件的影响因素。常规的影响因素一般有摄影交会角、拍摄数量、拍摄距离、曝光强度、标尺尺寸、标志点特性等。国内外已经有很多专家 学者对这些影响因素进行了研究，并找到了相应的降低影响的方法，本文不再赘述。

本文仅研究真空低温环境对摄影测量的影响。真空低温环境条件下，配装温控小舱可为相机提供常温常压干燥的环境，故真空低温环境下与大气条件下唯一不同的是在摄影成像光路上增加了光学窗口。温控小舱上的光学窗口改变了成像光路，进而影响摄影测量精度；同时，真空低温环境会改变光学窗口面形，也将影响摄影测量精度。本文将从影响的原理出发，针对光学窗口分析其对测量精度的影响，并结合仿真和试验研究影响的程度。

1 真空低温环境对摄影测量的影响

1.1 摄影测量精度影响原理

采用摄影测量方法测量被测物坐标的原理是：使用相机从不同摄站对被测物进行拍摄，每次拍摄都可获得被测物在CCD 上的1 个像点坐标，最后基于所有像点坐标，解算出被测物的三维坐标（如图1所示）。

像点与被测物坐标的关系用共线方程[3]表征为

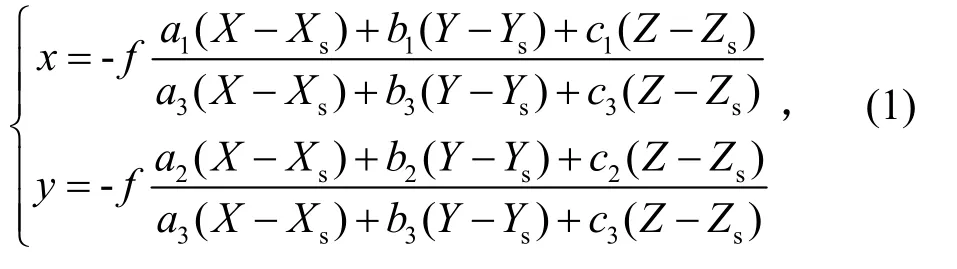
式中：a1、a2、a3、b1、b2、b3、c1、c2、c3为组成从物方空间坐标系到像空间坐标系的旋转变换矩阵[4]的9 个参数，是3 个独立的旋转角的函数；X、Y、Z是像点在物方空间坐标系下的坐标；Xs、Ys、Zs是投影中心在物方空间坐标系下的坐标；f为光学系统主距；x、y为像点坐标。

实际成像时，主点的像平面坐标不严格为0，而存在一微小值，如图2所示，记为(x0,y0)。

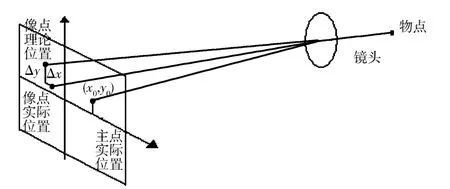
图2 摄影测量实际成像示意图 Fig.2 Actual imaging diagram of photogrammetry

在真空低温环境下使用摄影测量方法时，摄影测量光路必须经过温控小舱上的光学窗口，而光学窗口对光路的改变可等效于摄影镜头的物镜畸变，使得像点在像平面上相对其理论位置(x,y)存在偏差(Δx,Δy)，因此实际共线方程为

如式(2)所示，当进行上述的等效时，除像点偏差外，其他参数均未发生改变，故测量精度影响的本质是像点偏差。综上，真空低温环境对摄影测量的影响可以分为3 个方面：第一，光学窗口的增加使光路上增加介质，改变光路导致像点偏差；第二，真空环境改变光学平晶面形导致的像点偏差；第三，低温环境改变光学平晶面形导致的像点偏差。本文将通过偏差分析得出真空低温环境对摄影测量精度的影响程度。

1.2 增加光学介质的影响

1.2.1 影响分析和仿真

由折射定律和光学成像的几何原理[5]可知，在原有的光路中增加光学介质，使光线在经过不同折射率的介质（空气和光学窗口）时发生改变，导致成像点位置改变，即在相机的成像面上的像点坐标发生变化，影响测量精度。

用Zemax光学仿真软件可获得增加介质对成像的位置和距离的影响。对直径为170 mm、通光孔径为160 mm、厚度为17 mm 的光学窗口（光学平晶）进行建模，将长度为800 mm 的被测物放在距离光学窗口2 m 的位置，由于相机镜头紧贴窗口，故被测物距离相机镜头的实际距离为2017 mm。光路仿真（图3）显示，被测物经过光学窗口在距离镜头 2 011.521 mm 处形成长度为800.023 mm 的虚像（黑色是被测物，红色是虚像），测量误差为0.023 mm。

图3 增加介质影响的光路仿真 Fig.3 Imaging simulation of the influence by inserting materials

1.2.2 大气条件下的对比试验

1）试验方法

试验前先将回光反射标志点（图4中的白色点状物）均匀贴在4.2 m 长的试验场中，在光学平台上利用2 个回光反射靶球设定800 mm 的长度作为被测量的标准长度，并用测量精度为0.7 µm 的激光跟踪仪对其进行测量，结果为799.306 mm，即以此作为本研究中被测物长度的真值。基于摄影测量方法的解算原理，需要2 根长度为1.5 m 的铟钢标尺用于最终求解结果。1 号标尺平行于800 mm标准长度放置，2 号标尺与800 mm 标准长度呈75°长角放置，如图4所示。使用V-STARS INCA3 单相机摄影测量系统先直接对被测物进行测量，再带光学平晶进行测量。所用光学平晶直径为170 mm、厚度为17 mm，是温控小舱光学窗口的备件，其材料是杨氏模量为7.3×1010Pa、泊松比为0.17、密度为2.202×103kg/m3、折射率为1.46 的熔凝石英 玻璃。

图4 摄影测量试验布局Fig.4 Layout of photogrammetric test

2）测量过程及结果

在距离800 mm 标准长度2 m 处，用V-STARS相机不带光学平晶和带光学平晶分别对图4中的标尺及4.2 m 长的控制场进行5 次拍摄测量。控制场标志点、摄站和基准尺分布分别如图5和图6所示，其中绿色光线表示拍摄某个标志的摄站位置的相机光轴，蓝色方块表示相机。

相机不带光学平晶和带光学平晶5 次测量的平均值分别为799.284 和799.244 mm，相差 0.04 mm，与激光跟踪仪测量值相比较分别相差0.022 和0.062 mm，与仿真结果中的测量误差（0.023 mm）相近。根据厂家的产品手册，试验所使用的测量系统拍摄范围在4 m 之内的理想精度为0.025 mm，故引入光学窗口而带来的测量误差是理想精度的1.6 倍。

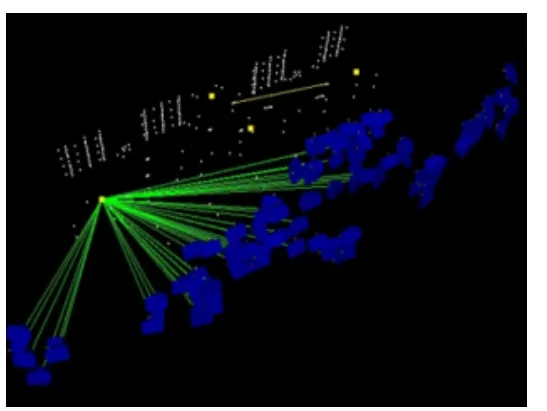
图5 单相机摄影测量试验结果 Fig.5 The result of single camera photogrammetry test

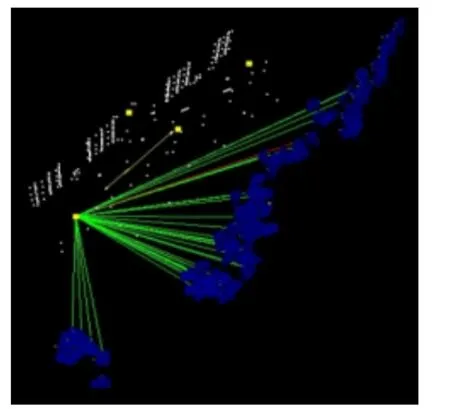
图6 复合摄影测量试验结果 Fig.6 The result of compound photogrammetry test

1.3 真空环境改变光学窗口面形的影响

1.3.1 理论分析

温控小舱内部环境是常温常压的自由换热状态（压力为1 个大气压，温度为25 ℃），因此外部真空环境使光学窗口两侧有接近1 个大气压的压力差。压力差均匀作用于光学窗口表面，导致光窗面形改变，进而影响光学系统。利用文献[6]中的方法，以1.2.2 节试验中所使用的光学平晶的参数为基础，计算出的光学平晶相对原表面的中心变形量最大为1.405 µm。

1.3.2 力学仿真

1）仿真模型

利用ANSYS 软件对1.2.2 试验中所使用的光学平晶进行模型仿真。根据上述温控小舱光学窗口的实际使用情况，确定只有在以光学窗口中心为圆心、半径80mm 的圆形范围内会受到1 个大气压的均匀作用力，故仿真时将不受力部分设定为固定约束不变形，如图7、图8所示。

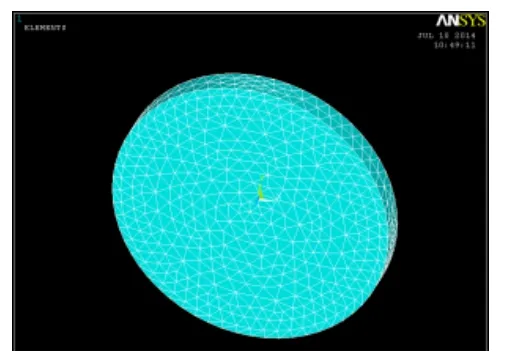
图7 光学平晶的有限元分析模型 Fig.7 Finite element model of optical flat

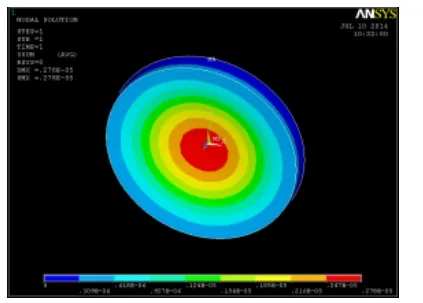
图8 光学平晶位移分布云 Fig.8 Contour of displacement distribution for optical flat

2）仿真结果

ANSYS 将光学平晶的模型划分为1351 个节点，相对原平面的最大变化量为2.780 µm，与理论计算的最大变化量1.405 µm 属同一数量级。模型受力变形后每个节点的三维坐标如表1所示。

表1 光学平晶变形后节点坐标 Table1 3D coordinates of node for deformed optical flat m

1.3.3 光路仿真

由于ANSYS 仿真后所得结果是离散的节点坐标，无法直接在光学仿真软件Zemax 中建模，需要将变形后的节点坐标拟合成曲面。本文基于文献[7]中的曲面拟合原理和文献[8]中的计算方法，利用MATLAB 的lsqcurvefit 函数，将变形后得到的光学窗口上、下表面各节点的三维坐标分别拟合成2 个球面。经过计算，下表面（相机一侧）的曲率半径为1330 m，上表面（被测物一侧）的曲率半径为1120 m，经过MATLAB 拟合的曲面相对原平面的最大变化量为2.620 µm，与ANSYS 仿真的变形量2.780 µm 近似，上、下表面的节点与拟合面的最大偏差分别为0.180 µm 和0.340 µm，表明拟合曲面是可以接受的。

基于上述拟合获得的2 个球面，在Zemax 光学仿真软件中进行建模，将长度为800 mm 的被测物放在距离光学平晶表面2 m 的位置（被测物距离相机镜头2017 mm，含光学窗口厚17 mm）。如图9所示，被测物通过变形后的光学窗口在距离镜头 2 011.771 mm 处形成长度为800.125 mm 的虚像。

图9 真空环境改变面形影响的光路仿真 Fig.9 Imaging simulation of the influence by shape change in vacuum

1.4 低温环境改变光学窗口面形的影响

1.4.1 理论分析

低温环境与舱内的常温环境可能会导致光学窗口产生轴向温度梯度，继而改变光学窗口的弯曲度。Barner 给出了一个经典的处理热对空间光学影响的方法[6]。均匀的轴向照射，可以使一个平行平面的光窗就变成一块轻度的同心弯月透镜[6]，它的平均曲率半径R由公式1/R=αq/k给出，其中：α是材料的线性热膨胀系数；q是单位面积上的热通量；k是材料的热导率。本文所研究的光学窗口材料的线性热膨胀系数是0.58×10-6/K，热导率是1.37 W/(m·K)。

如图10所示，温控小舱的舱壁控温到25 ℃，由于光学窗口比较薄，且采取压边安装方式，所以光学窗口的温度主要由舱壁导热控制，即在传热平衡时可认为光学窗口内外表面的温度均接近25 ℃。本文研究的换热模型可以简化为温控小舱外-170 ℃的热沉与光学窗口的辐射换热模型，并可进一步等效为表面积A2比表面积A1大得多的平行平板间辐射换热模型[9]。

图10 摄影测量系统温控小舱 Fig.10 Temperature control module in photogrammetry system

由公式(3)可求得辐射换热量Φ1,2及热通量q，

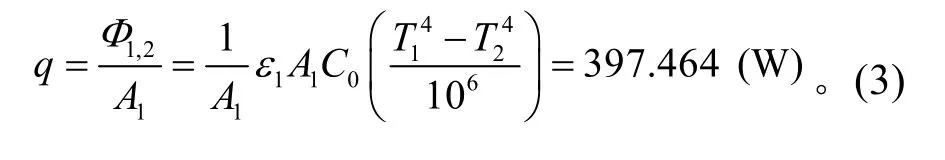
式中：热沉发射率ε1=0.9；黑体辐射系数C0= 5.67W/(m2·K4)；A1为直径160 mm 光学窗口的有效表面积；光学窗口温度T1=298.15 K；热沉温度T2=103.15 K。将求得的热流量q代入公式1/R=αq/k，即可求出光学窗口由于轴向温度梯度影响导致变形后的曲率半径R为5 942.848m。

1.4.2 光路仿真

依据1.4.1 计算获得的光学窗口曲率半径R建立同心弯月透镜模型，并进行光路仿真获得成像的位置和距离。如图11所示，被测物通过变形后的光学窗口在距离镜头2 011.525 mm 处形成长度为800.024 mm 的虚像。

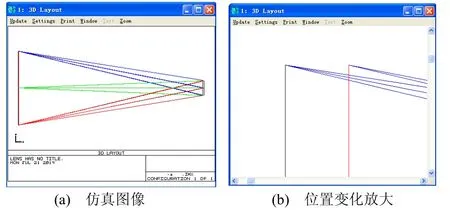
图11 低温环境改变面形影响的光路仿真 Fig.11 Imaging simulation of the influence by shape change in cold

2 仿真结果分析

分析真空低温环境对摄影测量的影响，需要将上文所有光路仿真中成像的位置和距离的结果转化为CCD 上的像素值，因为摄影测量最终的结果是基于CCD 上所记录的像素值进行算法处理后所 获得的结果。在本文的仿真中，被测物由于不同面形的光学平晶形成虚像，这种成像状态可以等效为在虚像的位置放置与虚像完全相同的实物，并去除光学平晶。相机成像可等效为小孔成像模型，根据相似三角形几何原理，可以算出被测物在CCD 上的尺寸。如图12所示，根据摄影测量学中视场角与焦距、CCD 尺寸的关系可计算出CCD 尺寸，进而利用被测物在CCD 上映射的尺寸、CCD 尺寸和CCD 分辨率可计算出所有仿真结果在CCD 上的像素值。计算使用1.2.2 试验中所使用相机的参数，焦距为21mm，视场角为77 场×56 场，分辨率为 8M（3500×2350）。

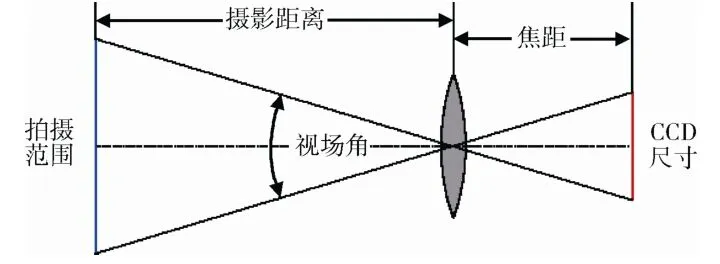
图12 视场角与焦距、CCD 尺寸的关系 Fig.12 Relationship between angle of field,CCD size and focal length

由表2的对比结果可知，增加光学平晶会使像高增加2.402 1 个像素；真空环境或低温环境对光学窗口面形的改变所导致的像高增加量不超过0.002 8 个像素。由于目前图像处理的定位精度为0.02 个像素，故面形改变的影响可以忽略，说明虽然本文没有做真空低温环境下的试验，但真空低温环境对精度的影响可以近似用大气环境下带光学窗口的试验结果来表征。

表2 仿真结果对比 Table2 Comparison of simulation results

3 结束语

综上可知，在真空低温环境中进行摄影测量时，引入光学窗口所导致的影响因素有光学介质的折射、压力差和轴向温度梯度导致的面形变化。其中主要影响是光学介质的折射，其引起的精度误差与摄影测量系统的精度属同一数量级，不可忽略，需要采用其他方法对其进行优化；而面形变化的影响在使用摄影测量方法时，相比摄影测量系统自身 精度可以忽略。可以在有试验条件时，用标准铟钢杆在真空低温环境中进行验证试验。

随着图像处理技术和摄影测量系统设备的进步，以及未来对摄影测量方法更高的精度追求，真空低温环境下光学窗口面形改变而导致的精度误差将不能忽略，未来的工作重点是分析对更高精度的影响，并提出优化方法。

（References）

[1] 蒋山平,杨林华,许杰,等.真空低温环境下卫星天 线变形摄影测量技术[J].光学技术,2013,39(4): 313-317 Jiang Shanping,Yang Linhua,Xu Jie,et al.Photogrammetric measurement of deformation for satellite antennas in vacuum cryogenic environment[J].Optical Technique,2013,39(4): 313-317

[2] 蒋山平,杨林华,于江.真空低温环境用高精度CCD摄影测量系统[J].航天器环境工程,2010,27(3): 361-363 Jiang Shanping,Yang Linhua,Yu Jiang.A high accuracy CCD photogrammetry system used in the vacuum cryogenic environment[J].Spacecraft Environment Engineering,2010,27(3): 361-363

[3] 黄桂平.数字近景工业摄影测量关键技术研究与应用[D].天津: 天津大学,2005: 17

[4] 蔡自兴.机器人学[M].2 版.北京: 清华大学出版社,2009: 18-19

[5] 吴健,严高师.光学原理教程[M].北京: 国防工业出版社,2007: 60,64

[6] 约德.光机系统设计[M].3 版.周海宪,程云芳,译.北京: 机械工业出版社,2008: 754-756

[7] 邓德标,方敏源,赵子龙,等.空间球状物体的数据采集与分析[J].测绘科学,2013,38(5): 146-148 Deng Debiao,Fang Minyuan,Zhao Zilong,et al.Data acquisition and analysis of space sphere[J].Science of Surveying and Mapping,2013,38(5): 146-148

[8] 张国雄,张德芬.四点法测量球心和球半径的最优方案[J].计量学报,1993,14(4): 247-250 Zhang Guoxiong,Zhang Defen.Optimization of four-point method about measuring sphere center and radius[J].Acta Metrologica Sinica,1993,14(4): 247-250

[9] 杨世铭,陶文铨.传热学[M].3 版.北京: 高等教育出版社,1998: 245,277