基于动态规划的肠衣搭配模型与软件设计
2015-12-23李辉
李 辉
(西南科技大学制造科学与工程学院,四川 绵阳 621010)
1 问题的重述
原料按长度分档,通常以0.5 米为一档,如:3-3.4 米按3 米计算,3.5 米-3.9 米按3.5 米计算,其余的依此类推。表1 是几种常见成品的规格,长度单位为米,∞表示没有上限,但实际长度小于26 米。
根据以上成品和原料描述,设计一个原料搭配方案,工人根据这个方案“照方抓药”进行生产。公司对搭配方案的具体要求见2011 年竞赛题。
2 问题分析
原问题的本质,是对肠衣原料按成品规格进行组装的问题。由于所生产的成品有三种规格,并且三种规格所对应的最短长度和最大长度、根数等不相同,因此应该先把原料表分为三种规格的原料表。由于要求充分利用原材料,并且剩余的原材料可以降级使用,因此应该考虑从第三种规格的成品开始组装,再依次组装第二种成品、第一种成品。通过上述分析和本文要解决的问题,有以下两个问题需要解决:
1)穷举运算量巨大,如何降低问题的规模。成品的组装,是从符合成品规格的原料中,选择一组合适的原料,满足根数、总长度等要求,即得到一个成品(捆),比较容易想到穷举的办法。但是,以题目中给出的数据,计算机运算量是巨大的,如何保证给定一组原料数据时,可以在30 分钟以内给出搭配方案,是建立数学模型要解决的关键问题。
2)如何降级处理。例如,当成品三的长度为18 米的原料有剩余时,采用何种方式进行分割的问题。
3 问题的假设
1)以0.5 米为一档,如:3-3.4 米按3 米计算,因此每一根都是有误差的。在组装的过程中,不考虑累积误差对成品总长度的影响。
2)假设原料描述表中给出的根数和长度数据都是准确的。
4 符号说明
xij——表示第j 种规格的原料放到第i 个成品(捆)的根数;
cj——表示第j种规格原料的总根数;
mj——表示第j种规格原料的长度;
yi——第i 捆是否成为一个成品,0-1 变量,0 表示不能;
n——原料总的规格种数;
w——假设模型可求得的最大捆数,比理论上计算的数据稍大即可;
v——某种规格的成品,每捆所包含的根数。
5 模型建立与求解
问题的实质是根据题中的原料情况,建立适当的数学模型,通过计算,给出合理的搭配方案,以方便工人“照方抓药”。根据对问题的分析,用0-1 变量yi表示能否组装成一个成品。我们可以根据题目中给出的数据,计算理论的成品数量。例如,对于符合成品三规格的原料,我们可以求得其总长度为∑mjcj,理论上可以组装成品的最大捆数为∑mjcj/89,约为136.62 捆,即最大可组装136 捆。理论上,只要假设的值为137,再通过LINGO 软件求得到的结果就是最大的成品捆数。
5.1 建立线性规划模型
基于该思路,我们建立如下的数学模型:
决策变量:xij,表示第j 种规格的原料放到第i 个成品(捆)的根数;
目标函数为:Max=∑yj
约束条件:
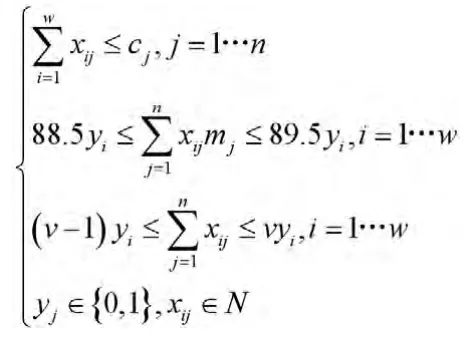
由于三种成品不同规格,因此需要根据上述思路建立三个类似的线性规划模型。
在实际的计算中我们发现,基于该模型的LINGO 程序在进行成品二和成品三搭配方案的运算时,经过长达9 个小时的计算仍然未能得出结果。而在进行成品一的计算时,LINGO 仅需要1 秒钟左右的时间。
5.2 建立动态规划模型
在前面的计算中,我们发现当w——假设模型可求得的最大捆数,它的值取得较小时,LINGO 的运算速度很快,比如取w=10 时,程序运算需要1 秒。此时的最优值,并非原料所能组装成该种规格的成品的最大捆数,而是从原料中选取了部分,组成了10 捆。
受此启发,如果不断的运行该程序,每次仅从原料中选取一部分,组装成10 捆,把用掉的原料从总的原料中减去,更新库存。下一次运算时,从上一次剩余的原料中,再选取一部分组装成10 捆,依次这样处理下去……直到所剩原料已经不足以组成1 捆(即最优值返回0时)为止,结束运算。
5.3 关于原料降级处理的措施
在上述讨论中,我们为了充分利用原料,将剩余的原料做降级处理。拿长度为14 米的材料为例,如果有剩余,它可以和长度介于7-13.5 米的进行捆扎,成品属于7-13.5 米的规格经过分析,大概分为以下三种措施:
①直接降至下一级的最大长度。如将剩余14 米长度的原料,割成13.5 米,即从成品三的原料变成成品二的原料,并且是成品二的最大长度。采用这样的降级处理办法,操作简单,程序设计中容易实现,但是对原料浪费比较大。
②对半分割。观察三种规格的成品的原料长度,可以发现,上一级剩余的原料,无论长度是多少,对半分割后都能落在下一级的长度区间内。采用这样的降级处理办法,操作简单,程序设计也容易实现,比第一种办法更节约原料。
③按一定的尺寸,将其分割成不相等的两段或者两段以上。根据组装过程中所缺少某种长度的原料,将剩余原料切成该种长度的原料。例如,在对成品三的组装中,14 米长的原料有剩余。在下一阶段,对成品二的组装中,11 米的原料紧缺,即将14 米的原料切成11+3米,11 米的降到下一级使用,3 米的降到再下一级使用。这样的降级处理办法看似比较科学,但是在动态规划过程中,很难得到哪种原料紧缺的数据。因此,在实际操作中比较困难。
5.4 利用EXCEL 和LINGO 开发肠衣搭配软件
如果单纯依靠LINGO 软件逐步进行求解,每进行一次运算,都要对矩阵xij中的数据进行分析,统计每一种长度的原料用掉了多少根,并计算剩余多少根,更新库存。接着,修改LINGO 程序中的数据,再次进行运算。在对成品三的计算中,xij变量的个数达到10×24 个,统计起来很繁琐,容易出错,并且需要较为专业的人员才能看懂LINGO 的结果报告,不便于公司的应用。
为了使操作更加简单有效,我们将肠衣原料数据输入到excel 电子表格中,并在LINGO 中使用excel 表格的数据,将每次运行LINGO程序的结果返回给excel 电子表格的指定区域。配合使用VBA 和宏,对每次运算结果进行整理,统计用掉的原料根数、更新库存量,并把搭配方案以“药方”的形式通过二维表反馈给用户,用户界面如图1 所示。
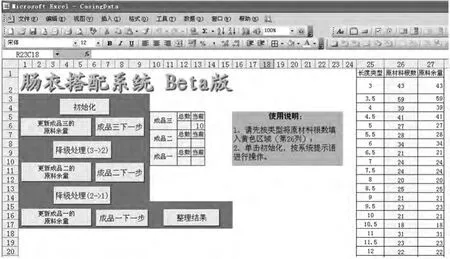
图1 系统用户界面
在图1 所示的“肠衣搭配系统Beta 版”中,通过编写VBA 程序,将每次运行LINGO 得到的数据进行统计分析,更新原料余量,所有操作都转化为简单的鼠标操作。下面对具体的操作做简单的说明。
①打开名为“CasingData.xls”的EXCEL 电子表格;
②将原料描述表的数据,对应输入第26 列;
③单击初始化;
④按弹出对话框的提示,打开LINGO 程序,求解名为“阶段三”的LINGO 程序,如图2 所示;求解完成后,切换到excel 窗口;
⑤单击“更新成品三原料余量”,可以看到在EXCEL 窗口的右边,已经有了10 种搭配方案;
⑥单击“成品三下一步”,按提示切换到LINGO 窗口,再次求解。求解完成后,切换到excel 窗口;注意,虽然这里求解的都是名为“阶段三”的LINGO 程序,但EXCEL 传递给LINGO 的参数已经改变,因此运算结果是不一样的。
⑦单击“更新成品三原料余量”,新的搭配方案已经追加到上一步方案的后面;
⑧当成品三的原料再也不能组装成品时,系统会提示采取降级处理。单击“降级处理(3->2)”,系统提示运行“阶段二”的LINGO 程序;
⑨同理,直至程序将成品一的原料搭配完成,提示“第一种规格的成品分配方案运算完毕,搭配完成!”时,表示运算已结束;
⑩单击“整理结果”,EXCEL 窗口的右边,方案已经给出,即是给工人的“药方”,成品一的部分捆数的搭配表如表1 所示,其它捆的“药方”形式也如表1 类似。
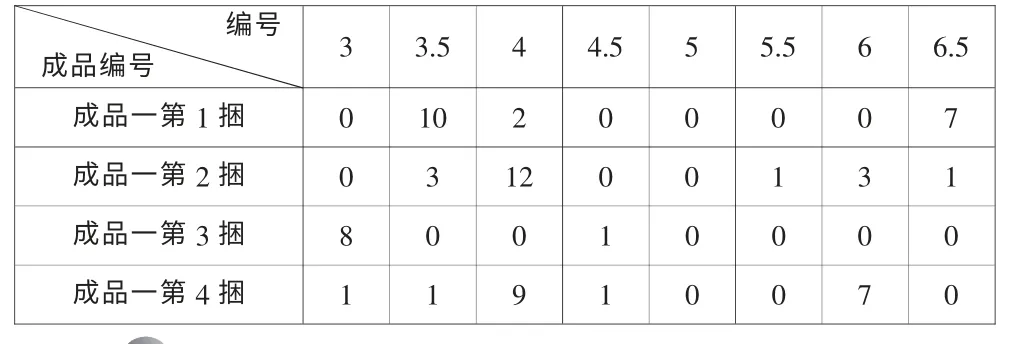
表1 成品一搭配表
[1]教材编写组,编.运筹学[M].3 版.北京:清华大学出版社,2005,6.
[2]谢金星,薛毅.优化模型与LINGO/lindo 软件[M].北京:清华大学出版社,2007.
