埃博拉病毒传染机制与研药策略的数模分析

纪元昕，朱家明，王茜瑶，胡学峰

（安徽财经大学统计与应用数学学院；安徽蚌埠233030）

埃博拉病毒经历了大爆发穿过非洲大陆在2014年，感染人数之多，死亡率之高引起了全球广泛关注。同时，埃博拉病毒的传染居然周期爆发性，主要针对非洲一带地区。因此研究埃博拉的传染机制与内在规律是进一步抵制并消除病毒的必要前提［1-3］；之后，是否应研制药物，研发周期与研药量均是需要解决的问题；最后，政府如何选取制药公司进行低成本高水平的制药开发是我们在疾病理论基础上展开实际解决方案的手段。

1 埃博拉病毒传染机制模型

1.1 数据分析

查找到Guinea，Liberia，Sierra Leone等国家感染人数各天累计的感染人数加和作为总体的患病情况，通过相关数据我们可以观察到的是在该病毒从爆发到传染的较长一段时间内该病毒，该病毒满足指数增长模型，该疫情被发现的前中期，因为缺乏必要的医疗手段和医疗常识，该病毒的繁衍速度可近似看作是自然条件下种群的增长［4-6］。

为了有效将时间进行排序，定义2014年3月25日为发现疫情的第一天，以后分别按照天数间隔进行排序，根据散点图的大概走势，猜测在前期及0～220 d之间，感染人数的增长趋势呈指数增长，令：x（t）=x0ert对函数进行拟合。

两边同时取 ln，y=rt+a，y=ln x，a=ln x0，利用 Matlab 输入相关数据处理得拟合函数：y=0.02x+4.7，x0=109.95；所以有：

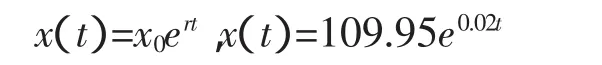
做出在0～300内的预测曲线和在真实变化趋势。

从图1中可以看出基本上在0～255 d内，感染人数基本上呈指数增长型趋势，但在255天以后真实的感染人数较指数增长明显减缓，这从宏观上说明埃博拉病毒的传播速度在一定程度上受到了阻碍。

1.2 模型建立

结合阻滞增长模型和SIS模型进行建模。

在人类还没有有效措施能够制止埃博拉疫情的传播并治愈已经感染的病人时，将埃博病毒的传播看成是一个病毒种群在自然环境下的种群数量增长情况。因此可以运用阻滞增长模型—logistic模型对其发展规律进行研究。

求出阻滞模型变化率曲线，得出在253 d时非洲三国埃博拉病毒的感染者增长率最大为320，大概从500 d开始，病人总数趋于稳定，最大感染人数为40000人。

现在针对三个国家的疫情在自然增长情况下分别进行建模。从三个国家的患病人数与时间变化图中，我们可以发现三个国家的感染情况基本符合阻滞增长的形式，这一点与总的趋势也相同。三个国家的患病人数初始阶段呈现指数增长模式，后来增加速度在250 d之后普遍出现变慢，这说明疫情在隔离，治疗等相关措施下受到了一定控制。

针对利比里亚，我们进行作图分析可得，见图2，3。

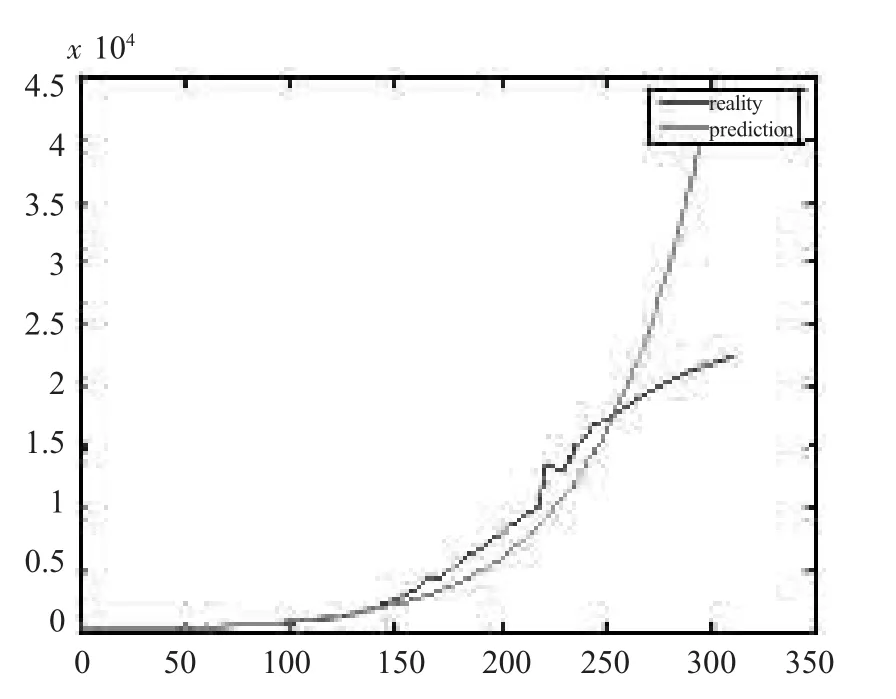
图1 预测曲线与真实曲线比较图

图2 利比内亚感染人数变化图

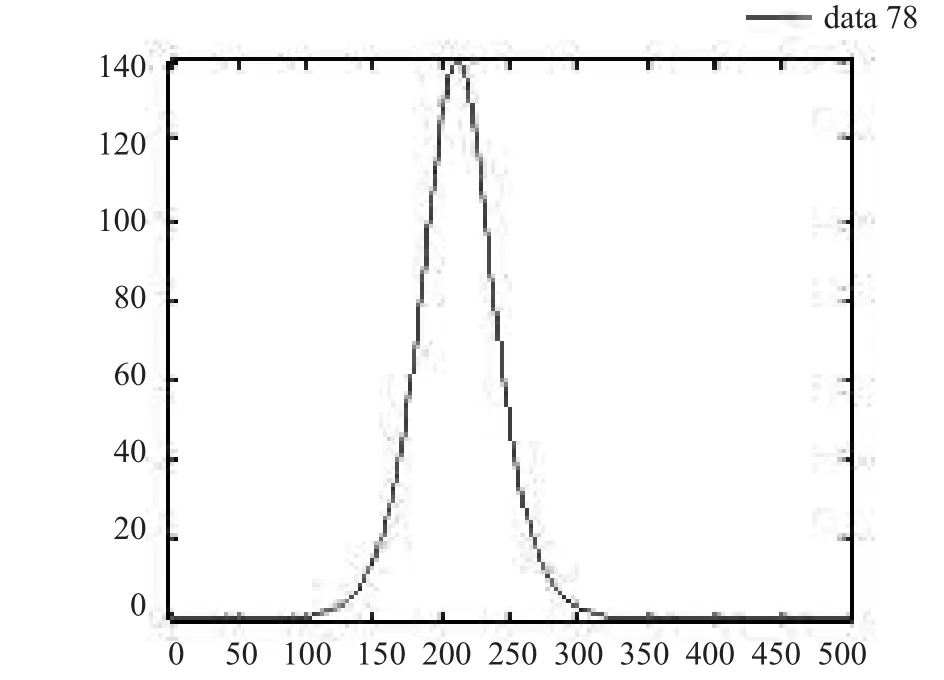
图3 利比内亚患病增加率

1.3 结果综述

从表中可看出，最早达到增长高峰的是几内亚为191 d，最迟的是塞拉利昂在256 d，按照患病前在人数的多少获取权重进行求和，研发期限最长为为244.35 d。

表1 各国患病情况信息表

2 药物研发必要性判别

2.1 研究思路

为了研究是否有其他疾病需要新药研制，我们选取该地区较为显著的疾病种类：肺结核，艾滋病与马来热。根据这三种疾病在该阶段内的感染人数，将其与埃博拉感染人数进行比较判断，进行方差检验，若有显著差异说明该种疾病需要新药的救治。在对疾病进行判断之后，我们对各疾病每年感染人数提取异常值，即疾病未得到有效控制有进一步爆发趋势的年份，将其作为研制新药的最迟开始时间，制药期限以病情下次大爆发为界，进行控制。

2.2 模型建立

由于在上一题中我们估测出了埃博拉病毒的感染人数，且该估测是在无其他新药开发的情况下得到的。因此在本题的求解中，我们可依据埃博拉病毒感染数作为基准来研究其他疾病感染的波动情况。由于疾病类型的复杂多样，为了简便计算，我们选取了乌干达地区较为显著的三大类传染性疾病：肺结核，艾滋病以及登革热。肺结核与艾滋病数据较为完整齐全，而登革热数据有所缺失，因此我们采用多项式拟合近似求的其他年份的感染数据。

根据现有的2000到2008年的乌干达登革热患病人数，用多项式拟合出2009-2012年的患病人数。具体患病数见图4。我们将登革热患病人数与肺结核和艾滋病感染人数进行简单加权作为总体患病人数进行综合分析。此时，为了判断该阶段是否需要研制新药，可将整体的疫情数据与之前估测的埃博拉感染数据进行方差分析检验，若有显著差异，说明整体的疾病未如同埃博拉一般得到一定控制，而有持续爆发加重的趋势，则需要研发新药。若无显著差异，则无需研制新药。

通过方差分析，得到：F=529.97，F 值较大，且 P=0＜0.05，通过了显著性检验，认为两个数据之间存在显著性差异，即总体疾病疫情上有存在其他疾病肆虐的情况，需要研发新药物进行治疗。

对于药物研制的最迟期限与可能的总产量，通过对每年的总体疾病感染人数进行观测，找出数据的异常波动点，作为研发开端的依据，并将药物研制周期控制在疾病的下一次异常爆发之前，使之得以投入市场，阻止疫情的下一次爆发。

通过Matlab做出总体患传染病人数的波动图，见图5。

由图可看出，在2004年以前总体疾病人数趋于平缓，但在2004年开始突然大幅度增长，说明此时有新的疫情的爆发，并为需研制新药的最佳开始时间。

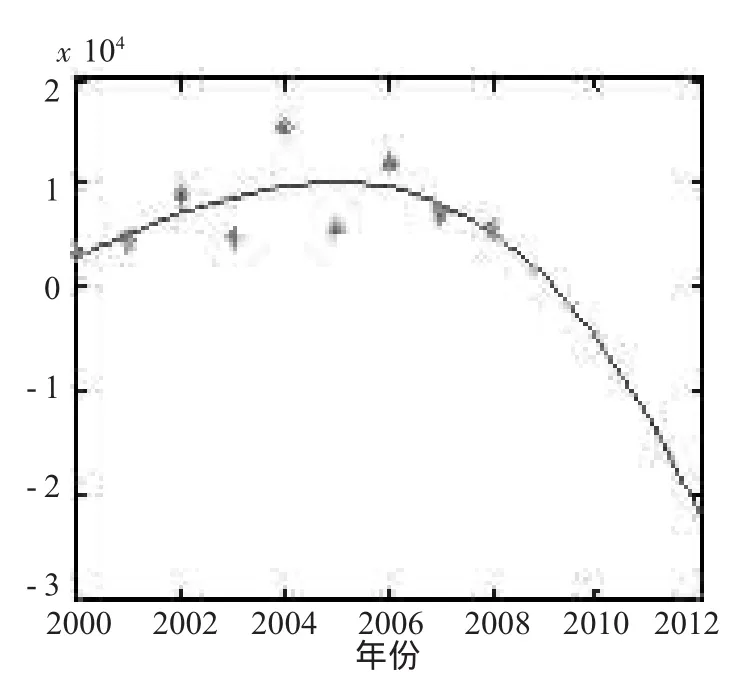
图4 登革热患病率变化图

图5 总患病人数波动图

3 制药公司的选取与合作

3.1 原理分析

考虑到公司联合降低制药要有效降低成本和风险，就需要在一定公司范围内选取关于制药过程中几个花费和风险最低的部分进行组合，这些部分来源的公司便是最优组合的公司。

我们选取科研攻关能力a，原材料生产能力b，药物检验能力c，药物后期跟踪与反馈能力d。

查阅文献资料，给出如下四个指标的计算公式：科研攻关能力a，原材料生产能力b，药物检验试验能力c，该公司资金流动能力d，并研究这四个指标对降低制药成本和风险的影响。

3.2 模型建立

对任一制药公司i，令x1为该公司科研部门人数，X是该公司总人数，平均研制一款新药的速度v1，平均每年专利申请数t，可建立数学表达式：

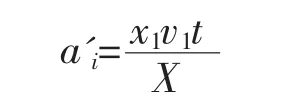
令y1为该公司近三年平均每年生产药物量，Y为同年该型药物研制总量，v2为平均生产一吨新药速度：

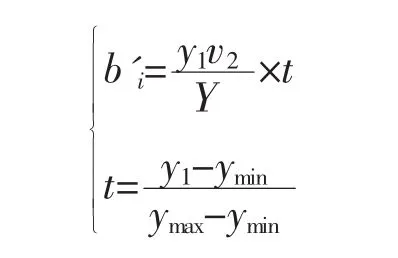
令ys为该公司该年生产实际销售该种药品总数，y为该年该药物生产量，v2为该公司检验药品科研人数，

令g，c分别为该年该公司近三年平均每年营业额和所有成本，r%为该公司营业额增长率，R为

建立一种限制数量上不断增长的方法：在选定的公司中如果对于一定范围内i=1，2…m…k（k≥m），随着i的不断增长T也不断增长。

首先对任意公司i求出其综合能力：T=λ1ai+λ2bi+λ3ci+λ4di然后按照综合能力排序 Tm＞Tk＞Tl＞…＞Tmin，按照从大到小的顺序依次作出构造一个在数量上随着i增长 T 不断增长的数列 y1，y2，y3…yn+k。求其增长速度 ρ，以及阈值η，在增长速度小于阈值时我们认为此时增加公司的数目已经没有必要。

因此，在满足条件时，选用公司组合进行联合制药的效率最高。

图6 ρ变化图

4 结论

以上各模型经过各软件的检验，具有一定的合理性。但同时模型的建立必须依靠必要的假设，在本文中我们假设埃博拉病毒与其他疾病无交叉作用，并在第二题运用第一题的埃博拉传染病模型时忽略该病毒的周期性，因此与实际的疾病数会有偏差。综上来说，我们依据埃博拉现有的感染病例数建立了较符合它传播特征的传染病模型。同时对药物研发方面进行了研究与推测，最后对制药公司的评估与选择提供了较新颖的理论方案。

［1］Xinxin Wang,Shengqiang Liu.An epidemic model with different distributed latencies ［J］.Applied Mathematics and Computation 2014,241:259-266.

［2］Li D,Gui C,Luo X.Impulsive Vaccination SEIR Model with Nonlinear Incidence Rate and Time Delay ［J］.MathematicalProblemsin Engineering,2013.

［3］Buonomo B,d’Onofrio A,Lacitignola D.Modeling of pseudo-rational exemption to vaccination for SEIRdiseases［J］.Journal of Mathematical Analysisand Applications,2013,404（2）:385-398.

［4］Zhang J,Jia J,Song X.Analysis of an SEIREpidemic Model with Saturated Incidence and Saturated Treatment Function［J］.The Scientific World Journal,2014.

［5］Liu M,Bai C,Wang K.Asymptotic stability of a two-group stochastic SEIRmodel with infinite delays［J］.Communications in Nonlinear Scienceand Numerical Simulation,2014,19（10）:3444-3453.

［6］Wang X,Wei L,Zhang J.Dynamical analysisand perturbation solution of an SEIR epidemic model［J］.Applied Mathematics and Computation,2014,232:479-486.