基于改进粒子群算法的EBG结构优化设计*

刘 东，田雨波

(江苏科技大学电子信息学院，江苏镇江212003)

LIU Dong，TIAN Yubo*

(School of Electronics and Information，Jiangsu University of Scienceand Technology，Zhenjiang Jiangsu 212003，China)

电磁带隙EBG(Electromagnetic Band Gap)结构的研究主要集中在微波与毫米波段。无论是在天线设计领域还是微波电路中，EBG结构都表现出优异的性能。EBG结构易于实现，便于集成，可以利用传统的制作工艺进行加工，方便简单。针对各种的EBG结构参数已经进行了很多的研究，然而，大多数对EBG结构的研究依赖于以往的经验［1－3］。

粒子群算法PSO(Particle Swarm Optimization)是由社会心理学博士James Kennedy和电子工程学博士Russell Eberhart于1995年提出的［4］，是继遗传算法之后，产生的一种全新的智能优化方法。它是一种演化计算技术，依靠个体之间的协作来寻取最优解。群体中的粒子有记忆功能，每个粒子通过跟踪粒子本身找到的最优解Pbest和群体找到的最优解Gbest，更新粒子的位置和速度，不断向最优解靠近，最终到达最优解。粒子群算法作为一种新的并行优化算法，其理论简单，收敛速度快，因此一经提出，立刻引起了优化和演化计算领域的学者们的广泛关注，并在短短的几年时间里出现了大量的研究成果，形成了一个研究热点［5－8］。

在实际应用的过程中，粒子群优化算法根据全体粒子和自身粒子的搜索经验向着最优解的方向发展，但是在进化后期收敛速度变慢，同时算法的精度不高，对于高维多极值的复杂优化问题，不同的学者提出了很多的改进方法，这些方法都不同程度地提高了基本粒子群优化算法的收敛速度和搜索精度。简化粒子群优化方法SPSO(Simple Particle Swarm Optimization)是一种改进的粒子群算法，该算法没有粒子速度参数，可以避免因设定该参数而影响粒子的收敛速度和搜索精度。贾瑞玉等在简化粒子群的基础上引入了动态改变权值［9］，许传敏等针对算法容易陷入局部最优的问题，引入了混沌理论来改进简化粒子群算法［10］。本文以SPSO算法为基础，结合文献［11］中对于标准粒子群算法的改进，得到了改进的简化粒子群优化算法ISPSO(Improve Simple Particle Swarm Optimization)，提高了SPSO算法的收敛速度和精度，将电磁仿真软件IE3D跟ISPSO算法结合起来用于EBG结构的优化设计。

1 ISPSO/IE3D算法描述

1．1 ISPSO 算法

粒子群算法的基本原理描述如下:一个由m个粒子(Particle)组成的群体(Swarm)在D维空间中以一定的速度飞行，这个速度是考虑到它自身和同伴的飞行经验来动态调整的，每个粒子在搜索时，考虑到了自己搜索到的历史最好点(Pbest)和群体内其他粒子的历史最好点(Gbest)，在此基础上进行位置和速度的变化。基本粒子优化方法的速度和位置更新的式子可以表示为:

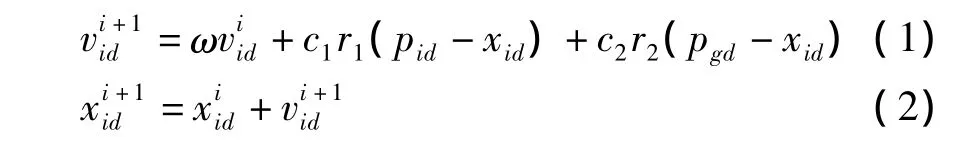
其中第i个粒子在第d维的位置表示为xid，其飞行速度为vid，该粒子的历史最优点为pid，整个粒子群当前的最优位置为pgd。c1和c2称为学习因子或者是加速系数，一般为正常数。vid∈［－ vmax，vmax］，vmax是用户设定的常数。r1和r2是在［0，1］区间内均匀分布的伪随机数。

胡旺等人在文献［12］中提出了简化粒子群优化算法，该算法可以没有粒子的速度这一概念，避免了人为确定参数vmax而影响粒子的收敛速度和搜索精度，由此粒子群优化的方程可以简化为:

本文做如下考虑:在标准粒子群优化算法中，2个随机参数r1和r2是相互独立的，如果这2项太大，那么pid和pgd会过度影响粒子位置的变化，如果2个参数太小，那么pid和pgd都没有被充分地使用。pid和pgd不应当对于粒子的位置变化具有同等的作用。本文将这个思想应用于标准粒子群优化算法提出了如下方法:

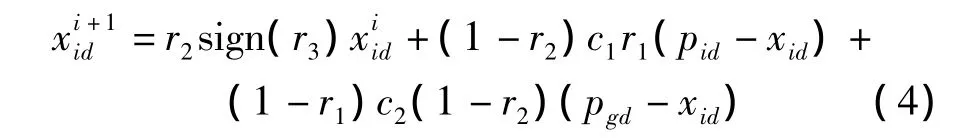
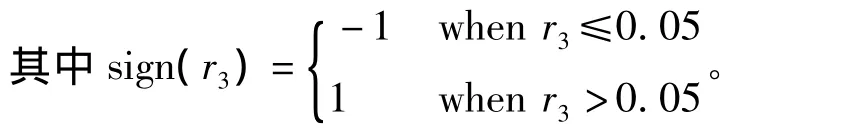
在式(4)中，式子根据粒子自身的惯性和经验来调整位置，本文中通过r2这一参数可以调整自身的惯性或者是粒子群的经验对于粒子位置影响的比重。同时，经验对于位置的影响又可以分为粒子自身的经验和其他粒子的经验，本文中通过参数r1来调整自身的经验或者是社会的经验对于位置影响的比重。同时，r3≤0．05 时，sign(r3)为 －1，表明粒子可以以很小的概率反方向搜索。改进的SPSO算法避免了过早地陷入局部最优，并且提高了SPSO算法的收敛速度和精度。

1．2 ISPSO/IE3D 算法

IE3D是一种最常用的电磁仿真软件，它基于MOM方法，能够方便、快速地分析和设计三维微带天线和高频印刷电路和数字电路以及平面贴片天线等。IE3D集成了全波电磁仿真和最优化包，给出了几种常用的优化算法，如鲍威尔优化算法、遗传算法和随机算法可以用于优化设计。但是由于IE3D本身对于结构变量定义的限制，其多个变量之间只能设置简单的线性关系，因此，无法对较复杂的结构进行优化。优化复杂的结构可能导致仿真结构的重叠，从而导致仿真中错误的产生。本文中，ISPSO算法通过外部编程调用IE3D电磁仿真软件，通过ISPSO算法优化结构参数，发送给IE3D进行仿真，并输出仿真结构，由ISPSO算法来对结构进行优化设计，判别是否达到最佳的设计参数。因此，复杂的结构变量可以通过ISPSO/IE3D来设置优化，其流程图如图1所示。在IE3D仿真软件中，仿真模型的结构参数储存在．geo文件中，其仿真控制参数(包括变量设置、频率设置、结构参数文件路径、结果文件存储路径等)则储存于．sim文件中。当开始对模型进行仿真时，仿真程序会读取模型的．geo和．sim文件中的参数设置，根据这些设置参数对模型进行计算。仿真结果则分别储存于几个文件中，其中s参数数据储存于．sp文件中。该优化设计方法采用批处理(．bat)文件调用IE3D的仿真程序，读取仿真结果文件中的数据，根据这些数据采用ISPSO算法更新．geo文件中的变量值，重复这个优化过程就可以实现ISPSO程序对EBG结构的优化，从而实现对EBG结构的自适应的优化设计。

图1 ISPSO/IE3D算法流程图

2 EBG结构优化设计实例

近年来，电磁带隙EBG(Electromagnetic Band-Gap)结构已经成为微波和毫米波领域中一个研究的热点课题，它的带隙形成机理和在电磁各个领域的应用都得到了广泛的理论和实验研究，证实了其在改善微波器件和天线性能方面具有明显的作用。在这些EBG结构中，共面紧凑电磁带隙UC-EBG(Uniplanar Compact Electromagnetic Band-Gap)结构受到了特别的关注。这种结构具有简单、平面、低损耗和易加工等优点。UC-EBG结构由于受自身谐振特性的限制，往往带隙宽度较窄，带隙深度较浅。这些问题在一定程度上限制了其发展。通过合理设计EBG结构尺寸可以在一定程度上改变其电磁性能［13－14］。但是由于EBG结构几何尺寸的复杂性，很难定量的估计每个参数的影响。本文通过ISPSO/IE3D设计方法实现对UC-EBG结构的优化设计，该算法在实现优化设计过程中无需人工干预，可自适应地完成整个优化过程。

2．1 EBG 的结构

与蘑菇型EBG结构在电源层和地层之间内嵌周期性结构不同，UC-EBG结构是在电源层的金属表面上光刻或腐蚀出周期性结构。通过对单元结构的特殊设计，使其等效为局域谐振特性比较强的并联LC电路，以增加单元的谐振性能，然后利用单元谐振时阻抗无穷大的特性，阻止谐振频率附近的电磁波传播，形成频率带隙。一种UC-EBG结构单元如图2 所示，其参数为(d，l，w，w1，g)。

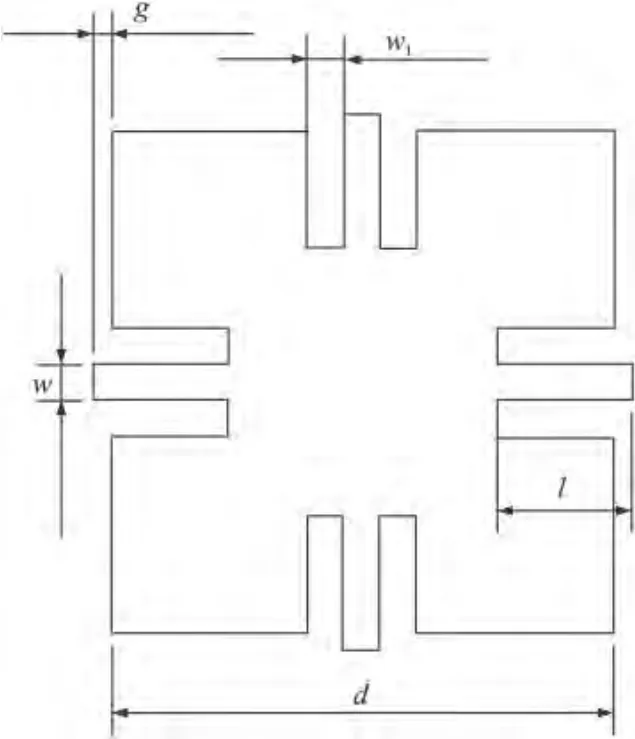
图2 UC-EBG结构单元及参数

图2所示的结构单元可由如图3所示的等效电路表示。该等效电路包含两个部分:第1部分通过EBG结构单元金属方块的等效电感Lp和等效电容Cp描述了单元金属块与地平面之间的传播特性;第2部分则描述了两个相邻单元之间的连接特性，其中Lb为对应桥接连线的等效电感，Cb为桥接连线的等效电容，Cg为两个相邻单元之间的等效间隙电容。该带阻结构的输入阻抗可表示为:

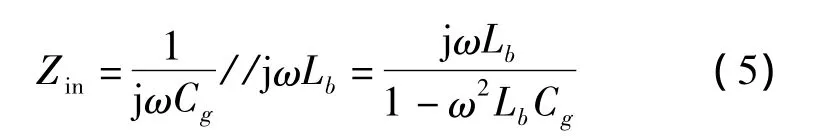
当Zin趋于无穷大时，得到截止频带的中心频率为:

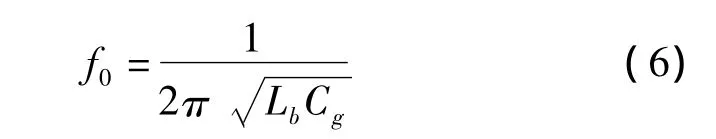
带隙宽度可由自由空间的波阻抗η和输入阻抗Zin之间的关系推导出，如式(7)所示:

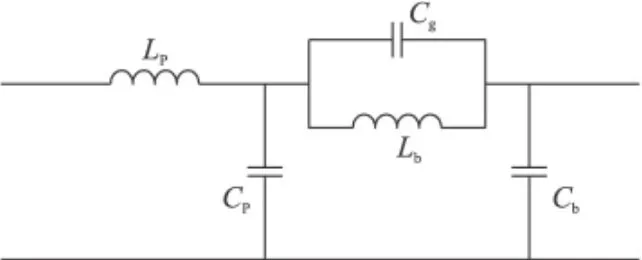
图3 UC-EBG结构的等效电路

2．2 算法参数设置

采用ISPSO/IE3D设计方法对UC-EBG结构进行了优化设计，以加深带隙深度，展宽带隙宽度。图2所示UC-EBG结构的相关参数取h=1 mm，UCEBG采用3×3的排列结构，其他参数通过本文算法进行优化设计，具体的优化参数和优化范围如表1所示。在UC-EBG结构优化中，ISPSO中粒子的维数设为5。为了减少IE3D仿真次数，加快优化过程，粒子种群规模取较小值8，迭代次数为100。优化程序中评价函数设置为:

表1 UC-EBG结构优化参数设置 单位:mm

2．3 模型仿真与结果分析

采用ISPSO/IE3D方法对图2所示的EBG结构进行了优化设计，优化后得到的EBG结构的结构参数如表2所示。为了验证该结构的带隙特性，利用悬置微带线法测量电磁带隙结构的带隙特性。

表2 采用PSO/IE3D优化得到的UC-EBG结构的参数单位:mm

图4为优化后UC-EBG结构与优化前UC-EBG结构的插入损耗S21特性曲线对比，其中两种UC-EBG结构的模型尺寸相同，都为90 mm×90 mm×1 mm。通过仿真结果可以看出:当抑制深度为－20 dB时，优化前UC-EBG结构的阻带范围为1．24 GHz～4．17 GHz，阻带带宽为2．93 GHz;优化后UC-EBG结构的阻带范围为 1．11 GHz～4．62 GHz，阻带宽度为 3．51 GHz。UC-EBG结构优化后相较于优化前阻带宽度增加了0．59 GHz，其带隙宽度有了明显的展宽，同时优化前最深 S21为83．9 dB，优化后的最深 S21为 93．6 dB。从图4可以明显看出优化后的UC-EBG结构的带隙特性明显优于优化前的结构。这一结果很好的验证了ISPSO/IE3D优化电磁带隙结构带宽和带隙深度的可行性和效果。

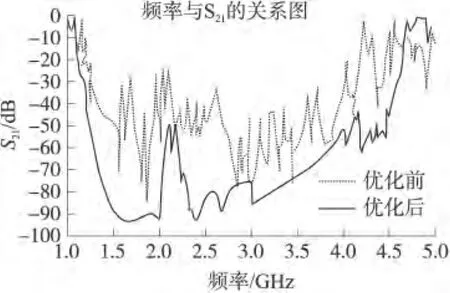
图4 优化前后UC-EBG插入损耗图

3 UC-EBG结构在天线中的应用研究

微带天线具有结构简单，易于制作，成本低，体积小，重量轻，低剖面，能与载体共形，能和有源器件、电路集成为统一的整体等优点，故而有着广泛的应用。但由于表面波、高次模、馈线损耗和介质损耗的影响，微带天线也存在着效率低的缺点。对于如何减小损耗，提高增益，以往的研究较少，通常的方法仅局限于采用较低的损耗介质，因材料的限制提高效率的手段十分有限。微带天线属于谐振式天线，其工作频带较窄，另外还会激励起高次模，以及有源天线由于有源器件的非线性而产生的伪辐射等，这些缺点都会降低微带的使用效率。近年来，许多学者致力于把EBG结构用于微带天线之中，如果将EBG结构应用于微带天线，就可以克服这些问题，从而提高微带天线的性能。本文将EBG结构应用于普通的矩形微带贴片天线上，采用EBG结构代替原来的金属接地底面，利用它的带阻特性抑制表面波，来提高天线的性能。

3．1 UC-EBG结构矩形微带天线

本文矩形微带贴片天线尺寸取为18 mm×24 mm，坐标原点取天线的几何中心，馈电位置为(－4 mm，0 mm)。介质板厚度1 mm，介电常数为4．3，地的尺寸为90×90。UC-EBG带隙范围为1．11 GHz～ 4．62 GHz，微带天线的谐振频率为 2．80 GHz，正好落在带隙内。图5给出矩形微带天线加入UC-EBG结构前后的回波损耗。从图中可以看出，加入UC-EBG结构后回波损耗明显好于未加入UC-EBG结构的天线。在2．8 GHz时，UC-EBG结构微带天线的E面方向图如图6所示，从图中可以看出加入 EBG结构后，天线的增益提高了1．3 dB左右。

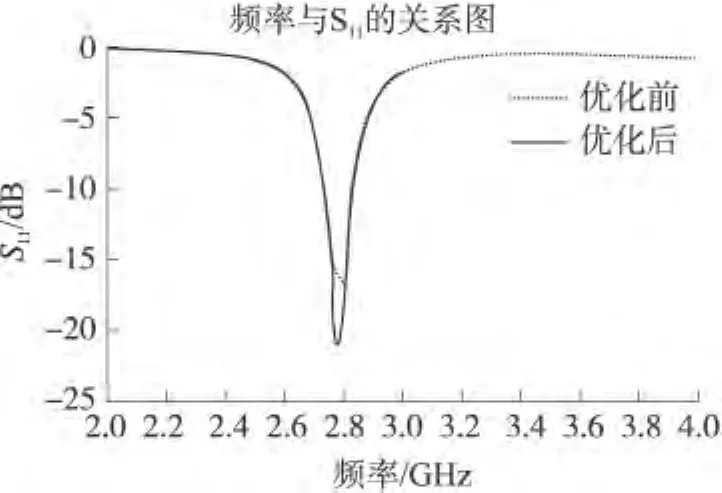
图5 天线加入UC-EBG前后回波损耗图

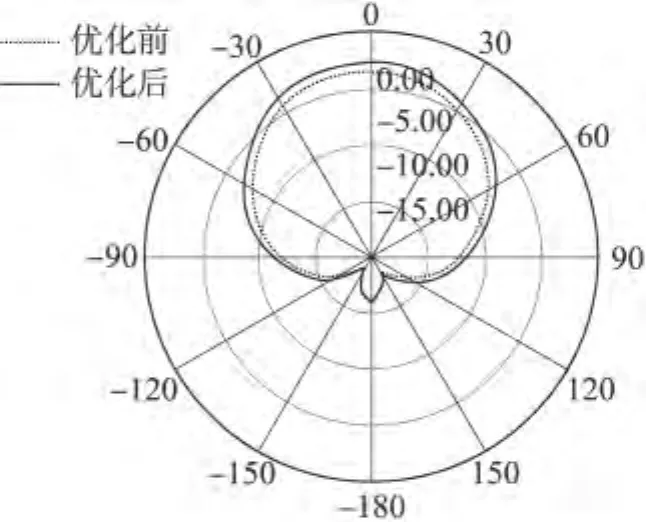
图6 E面方向图

4 结论

考虑到IE3D仿真软件本身对于结构变量定义的限制以及粒子群算法的局限性，提出了将IE3D电磁仿真软件和改进简化PSO算法相结合的方法优化设计电磁带隙结构，并以UC-EBG结构的优化设计为例验证了本文提出的算法。该算法在实现对电磁带隙结构的优化设计过程中无需人工干预，可以自适应的完成整个优化过程。从仿真结果可以看出，该方法通过ISPSO算法不断的调节UC-EBG结构的几何参数，可以展宽电磁带隙结构的带宽，并加深带隙深度，具有很好的实际应用价值。最后将UC-EBG结构应用于微带天线中，天线的回波损耗有明显降低，其增益增加了1．3 dB。

［1］ Abdelaziz A．Bandwidth Enhancement of Microstrip Antenna［J］．Progress In Electromagnetics Research，2006:311 －317．

［2］ Eva Rajo-Iglesias，Senior Member，IEEE，óscar Quevedo-Teruel，Student Member，IEEE，and Luis Inclán-Sánchez．Mutual Coupling Reduction in Patch Antenna Arrays by Using a Planar EBG Structure and a Multilayer Dielectric Substrate［J］．IEEE Transactions On Antennas And Propagation，2008，56(6):1648 －1655．

［3］ Haupt R L．An Introduction To Genetic Algorithms for Electromagnetics［J］．IEEE Antennas and Propagation Magazine，1995，37(2):7－15．

［4］ Kenndy J，Eberhart R C．Particle Swarm Optimization［J］．Proc IEEE Int Conf on Neural Networks．Perth，WA，Australia，1995:1942－1948．

［5］ 汪定伟，王俊伟，王洪峰，等．智能优化方法［M］．北京:高等教育出版社，2007:226－227．

［6］ 沙莎，彭涛，田雨波．双层EBG结构的优化设计［J］．压电与声光，2011，5(33):846 －848．

［7］ 张友俊，庞捷，李英．EBG在微波元器件方面的应用［J］．压电与声光，2005，27(3):291 －293．

［8］ 张友俊，张海峰，肖建康，等．刻蚀在导带边缘的PBG微带线［J］．压电与声光，2006，28(4):478 －480．

［9］ 贾瑞玉，黄义堂，邢猛，等．一种动态改变权值的简化粒子群算法［J］．计算机技术与发展，2009，19(2):137－139．

［10］许传敏，杨洪耕．电压波动估计的混沌简化粒子群算法［J］．电力系统及其自动化学报，2009，21(3):18－22．

［11］ Mandal D，Bhattacharjee A K，Ghoshal SP．Linear Antenna Array Synthesis Using Improved Particle Swarm Optimization［C］//2011 Second International Conference on Emerging Applications of Information Technology，Kolkata，2011:365 －368．

［12］胡旺，李志蜀．一种更简化而高效的粒子群优化算法［J］．软件学报，2007，18(4):861 －868．

［13］刘涛，曹祥玉，文曦，等．紧凑型电磁带隙结构的设计方法分析［J］．电子技术应用，2008，38(9):90 －92．

［14］ Jiang Ping，Xie Kang．Design of Novel Compact Electromagnetic Bandgap Structures with Enhanced Bandwidth［J］．Journal of E-lectronic Science and Technology，2010，8(3):262 －266．