三维激光点云数据的特征线光滑处理方法研究

王浩宇

(桂林理工大学 博文管理学院，广西 桂林 541006)



三维激光点云数据的特征线光滑处理方法研究

王浩宇

(桂林理工大学 博文管理学院，广西 桂林 541006)

摘要：在点云数据的三维建模过程中，常常会碰到特征线的光滑处理问题，通过拉格朗日插值、多项式拟合和三次样条函数拟合这3种方法对三维激光点云数据的特征线进行光滑处理.和原始数据进行实验对比分析，检验出样条拟合在特征线光滑处理方面有一定的优越性.

关键词：点云数据；光滑处理；拟合

在点云数据的三维建模过程中，经过各种算法得到的特征线一般都是折线.虽然三维激光扫描仪的数据采样比较密集，折线上点与点的距离较近，但是在一些远距离或者低密度的扫描过程中，得到的折线往往不能逼真地反映截面线的特征.因此,需要对折线进行光滑处理从而得到平滑的等值线[1]，本课题选取几种常见的特征线光滑处理方法进行了研究.

1几种常用的特征线光滑处理方法

1.1拉格朗日插值法

拉格朗日插值法是曲线拟合的一个重要方法，采用格朗日插值法进行插值多项式的构造如下：

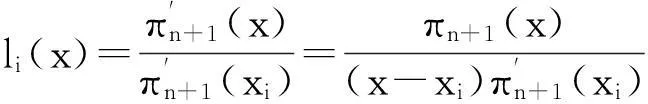
(1)

(2)

根据插值多项式的唯一性可知，满足条件的Ln(x) 就是要求的多项式,即拉格朗日插值多项式.

1.2多项式最小二乘曲线拟合

根据多项式的最小二乘原则，存在参数ak(k=0,1,2,…,n)可以满足所求的拟合曲线方程y=S*(x)，创造一个多项式为拟合曲线的方程式[2]，即

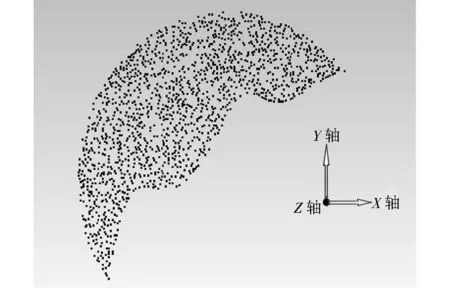
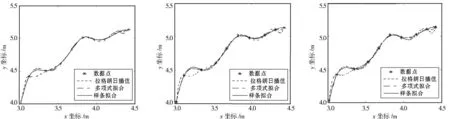
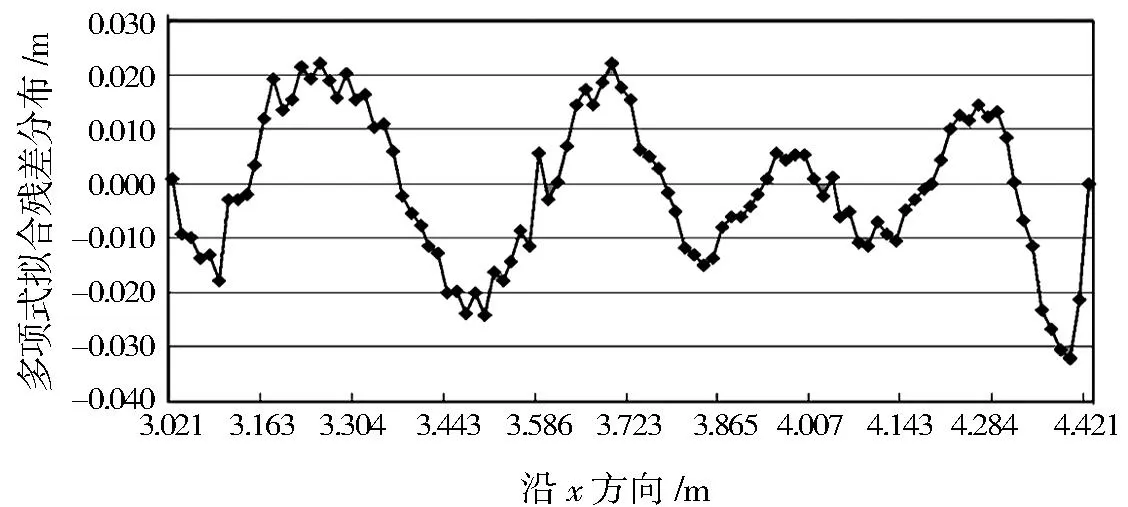
S(x)=a0+a1x+…+anxn, n

(3)

1.3三次样条函数拟合

目前，样条插值方法是函数逼近的重要工具,在大型加工行业的建模光滑处理上得到了广泛应用，伴随着航空、造船等加工业的要求越来越高,该方法也越来越占据重要的位置，其中三次样条具有二阶导数连续性也就是有很好的光滑性.

图1　产品的投影面轮廓点云图像Fig.1　Projection profile of a surfacepoint cloud image products

对三次样条插值函数定义如下:设区间[a,b]上给出一组节点a=x0

S3(xi)=fi, i=0,1,…,n,

(4)

则S3(x)为区间[a,b]上的三次样条插值函数.

2几种光滑处理方法的实验分析

2.1数据来源

经过前期去噪和去杂点等处理的一个工业产品在截面上投影的轮廓点云图像如图1所示.由该图像可以看出，轮廓的边界基本接近光滑，这为检验提供了实际的参考标准，实验数据如表1所示.

表1　物体的轮廓二维坐标

随机取其下侧较为弯曲边缘的二维坐标进行光滑处理的实验分析,数据越密折线表现得越趋近光滑，数据比较稀疏的情况下就表现为不光滑的折线.通过对物体边缘的二维数据进行精简，实验采用间隔性原则选取少量的边缘折线数据进行插值拟合实验，以检验插值拟合方法的逼近程度，寻找点数不多的时候更适合于光滑处理的拟合方法.对随机抽取的轮廓数据样本进行稀疏的抽取作为实验插值节点的数据，如表2所示.

表2　抽取的稀疏点云数据二维坐标

2.2数据分析

设采样阈值为n，则整个区间有n+1个点(包含边界值).当n=20时，采样间隔为0.07；当n=50时,采样间隔为0.028；当n=100时,采样间隔为0.014.根据n取值的不同，用不同的光滑处理方法进行处理，光滑处理效果如图2、图3和图4所示.

图2　n=20时不同处理方法的曲线图　　图3　n=50时不同处理方法的曲线图　　 图4　n=100时不同处理方法的曲线图Fig.2　Curve of different processing　　 Fig.3　Curve of different processing　　Fig.4　Curve of different processing　　　　method when n=20　　　　　　　 　　method when n=50　　　　　　　　　method when n=100

由图2可知，当n=20时，3种方法基本上都可以逼近所给数据点，但由于采样较少，出现部分折线，表现并不光滑.当n=50时,如图3所示, 此时3种方法都能够逼近数据点，其中多项式拟合方法和样条拟合方法的曲线较为光滑且走向一致，拉格朗日插值曲线在部分区段失真.由图4可知，当n=100时,3种曲线均逼近数据点，但拉格朗日插值曲线依然波动较大且逼近失真，处理并不理想，当n=100时，拉格朗日曲线在最后两个数据点之间有尖角产生.多项式拟合由于采样的增加，拟合光滑度在某些区段并不十分理想，只有样条曲线的光滑性比较好.

通过表1中原始数据的x坐标，由曲线求出相应的y坐标和表1中的原始数据y坐标进行对比来计算拟合的残差.分析得出,拉格朗日算术平均误差为-0.008 m,部分区段也明显出现了误差较大的情况,最大的误差达到0.11 m；多项式拟合算术平均误差为-0.004 m,部分区段拟合的结果也出现误差，最大误差达到0.032 m；样条拟合算术平均误差为-0.003 m,最大误差为0.006 m,逼近实验数据点.为了更直观地了解误差的大小趋势与分布情况，绘制了3种方法处理的误差图形,如图5所示.

图5　3种处理方法的处理结果残差Fig.5　Treatment results of three kinds of treatment methods of residual

由图5可知，3种处理方法中多项式拟合误差和拉格朗日误差部分区段有较大的偏差，只有样条拟合最逼近真值.对3种拟合方法的误差分布情况进行单独分析，误差分布情况分别如图6、图7和图8所示.

图6　拉格朗日插值误差分布Fig.6　Lagrange interpolation error distribution

图7　多项式拟合误差分布Fig.7　Polynomial fitting error distribution

图8　三次样条拟合误差分布Fig.8　Three times spline fitting error distribution

拉格朗日插值的误差波动分布状况如图6所示，残差波动太大且不符合正态分布，从残差分布不均匀可以看出这种方式的光滑处理并不理想.图7中多项式的拟合误差基本呈正态分布，但波动相对稍大.从图8中可以看出，样条拟合在一定的误差范围内呈现均匀的正态分布，由此可知样条拟合在数据处理光滑加密方面具有优势.

3结语

通过拉格朗日、多项式和三次样条对离散点云数据进行光滑实验对比和分析，寻找轮廓特征线光滑处理加密的适用方法.实验对比可知，当n取20,50和100时,曲线都能逼近数据点，而且3次不同取值的三次样条拟合曲线几乎重合，说明样条拟合在数据点相对较少的情况下也能做很好的光滑处理,验证了三次样条拟合更适合离散点云数据的光滑处理.

参考文献：

[1]王浩宇.基于地面三维激光扫描仪的数据处理及模型重建[D].桂林:桂林理工大学,2013.

[2]李庆扬.科学计算方法基础[M].北京:清华大学出版社,2004:88-118.

[3]曾长雄.离散数据的最小二乘曲线拟合及应用分析[J].岳阳职业技术学院学报，2010(3):96-99.

[4]李红广.基于B样条基粗糙惩罚的某些约束函数型数据光滑方法研究[D].上海:华东师范大学,2008.

[5]付培.低成本三维激光扫描仪系统关键技术研究[D].哈尔滨:哈尔滨工业大学,2010.

Smooth processing method of the feature lines of 3D laser point cloud data

WANG Haoyu

(BowenCollegeofManagement,GuilinUniversityofTechnology,Guilin541006,China)

Abstract:In the three dimensional modeling of point cloud data, researchers often encounter with smooth processing problem of characteristic lines. This study conducted the smoothing by Lagrange interpolation, polynomial fitting and three splines function fitting to smoothly process the feature lines of 3D laser point cloud data. Through comparison and analysis of experiment data and the raw data, it is concluded that spline fitting has certain advantages on characteristic line smoothing.

Key words:point cloud data; smooth processing; fitting

作者简介：王浩宇(1986-)，男，江苏徐州人，硕士，主要从事大地测量学与测量工程方面的教学与研究.

基金项目：广西空间信息与测绘重点实验室开放基金项目(桂科能1207115-22);桂林理工大学校级教育教学研究与改革项目(JYJG2013002);桂林理工大学校级精品课程建设项目(2013JPK03)

收稿日期：2014-10-24

中图分类号：P207

文献标志码：A

文章编号：1674-330X(2015)01-0058-04