基于逐步回归法研究Q345B成分及轧制规格与力学性能的关系

王翠娜 张大江 石成刚 贺瑞飞 杨雅玲

(安阳钢铁股份有限公司)

0 前言

为了生产出具有优良加工性能的产品，在不断优化和完善各种相关生产工艺的前提下，对钢材成分与性能之间关系的定量规律研究也日趋活跃。很多学者［1－5］都根据不同的限定条件，总结出了钢的性能与成分的经验公式，但由于每个钢厂实际生产控制水平不同，生产条件、设备状况等都复杂多变，这些公式在实际应用中经常出现计算结果与本厂实际生产相差较大，难以很好地指导生产。以往的回归分析中针对钢种的化学成分与力学性能的关系研究的比较多，轧制规格对力学性能影响较大，但是把轧制规格对力学性能的影响通过回归分析进行量化的研究比较少。

笔者结合钢厂生产现场的实际情况，利用生产过程中积累的理化检验数据及生产工艺数据，运用逐步回归的分析方法，研究了低合金钢Q345B 化学成分及轧制规格与力学性能的关系，建立了钢板性能的回归方程。回归方程的建立，可以有效地表示成分及轧制规格与性能指标的对应关系，有利于力学性能数据的分析。在保证整个轧钢生产工艺不做大的调整和变动的情况下，可以依据回归方程中的定量关系来描述、预测和控制产品的性能。

1 逐步回归分析方法

在实际问题中，人们总是希望从对因变量y 有影响的诸多变量中选择一些变量作为自变量，应用多元回归分析的方法建立“最优”回归方程以便对因变量进行预测或控制。所谓“最优”回归方程，主要是指希望在回归方程中包含所有对因变量y 影响显著的自变量而不包含对y 影响不显著的自变量的回归方程。逐步回归分析正是根据这种原则提出来的一种回归分析方法。

逐步回归分析的主要思路是按照自变量因子x1、x2…xn对因变量y 作用的大小，即用偏回归平方和的大小来衡量，由大到小逐个将因子引入回归方程。引入变量的条件是其t 统计量经检验是显著的，即每引入一个变量后，对已经被选入的变量要进行逐个检验，当原引入的变量由于后面变量的引入而变得不再显著时，要将其剔除。这个过程反复进行，直到既无显著的自变量选入，也无不显著自变量从回归方程中剔除为止。这样就保证了最后所得的回归子集是最优回归子集。本次研究应用统计学软件，设置可信度水平＞0．25 的因子被剔除，它既保证一定的显著性又能入选较多的自变量。

2 Q345B 逐步回归方程的建立及分析

2．1生产数据

本次研究统计数据为2014年某厂生产的Q345B 生产数据，包括化学成分、轧制规格和力学性能等，共计974 批。其中前100 批数据共10 个规格做为建立回归方程的样本数据，后面874 批数据共21 个规格做为回归方程的验证数据。Q345B 的化学成分控制范围及力学性能控制范围见表1、表2。

表1 Q345B 化学成分控制范围 /%

表2 Q345B 力学性能控制范围

2．2 回归结果

2．2．1 回归方程的建立及显著性检验

钢材的化学成分、生产工艺、取样部位、试样加工精度、人为误差等都会最终影响钢板的性能检验结果，如果将上述所有因素和条件全部进行考虑工作量太大，而且有的变量无法确定，因此，本次研究将钢材的五大常规元素及轧制规格作为回归变量自变量因子(其他残余元素含量低，影响小，不做考虑)，屈服强度和抗拉强度作为回归变量的因变量因子，利用逐步回归原理建立因变量与自变量的多元线性回归方程。回归方程式见(1)～(2)。

式中:ReL—屈服强度，MPa;Rm—抗拉强度，MPa;H—轧制规格，mm;C、Si、P—钢中化学成分，%;s—残差标准差，MPa;R—复相关系数。

方差分析表见表3、表4。

表3 屈服强度的方差分析表

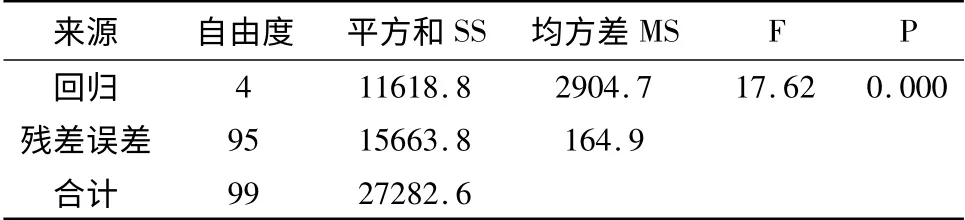
表4 抗拉强度的方差分析表

使用F 检验法对回归方程进行显著性检验。由表3 可知，屈服强度的方差分析中F=12．85，查F临界值表得F0．05(4，95)=2．46，从而有F ＞F0．05(4，95);由表4 可知，抗拉强度的方差分析中F =17．62 ＞F0．05(4，95)，说明各回归方程在α =0．05水平上显著。

2．2．2 回归方程分析

残差标准差s 越小，说明数据分布越集中，稳定性越好。复相关系数R 越接近1，说明相关程度越高;若R ＞0．5，说明自变量与因变量中度相关，关系可信。根据式(1)～(2)可以得出结论:屈服强度残差标准差是13．8 MPa，抗拉强度的残差标准差是12．9 MPa，说明抗拉强度比屈服强度稳定;屈服强度的复相关系数为0．6，抗拉强度的复相关系数为0．7，均大于0．5，说明该关系可信，同时抗拉强度自变量与因变量的关系比屈服强度更相关。

屈服强度和抗拉强度都与轧制规格、钢中碳含量、硅含量和磷含量存在相关关系。屈服强度和抗拉强度都随轧制规格增加而减小，随碳、硅、磷含量的增加而增加;碳、磷含量对抗拉强度的影响高于对屈服强度的影响;硅含量对二者的影响差别不大。轧制规格对屈服强度影响较大，对抗拉强度影响较小。

需要指出，某些元素在力学性能的回归式中没有出现并不意味着这些元素对它们没有影响，它们的影响可能在回归时隐含在常数项中［6］。此外，有些元素在某些回归式中的影响似乎与一般规律不同，这是因为各个生产阶段可能有些小差异以及各因素之间的交互作用造成的。

3 逐步回归方程的预测及验证

3．1 回归方程的预测

建立回归方程的重要目的是为了用来进行预测和控制。通过样本所建立的回归方程只是关于特征数的估计式，由此所得到的预测值也只能是一个估计结果，因此当利用回归式进行预测的时候，除了预测之外，还希望知道预测的精度即预测值的取值范围，本次预测精度如下:由式(1)可知，屈服强度的残差标准差为13．8 MPa，则用该回归方程进行预测，95%的误差不会超过±27． 6 MPa;由式(2)可知，抗拉强度的残差标准差为12．9 MPa，则用该回归方程进行预测，95%的误差不会超过±25．8 MPa。

3．2 回归方程的验证

通过验证，100 个样本数据回归方程的精度符合3．1 的预测精度，现用回归方程验证非样本数据，即如2．1 生产数据中所述的874 批次数据。经验证，屈服强度的误差在±27．6 MPa 内的数据占总批次的90．2%;抗拉强度的误差在±25．8 MPa 内的数据占总批次的92．3%。

为进一步验证回归方程的精度，将钢材性能的实测值与回归方程计算值的差值绝对值分区间讨论，以10 MPa 为区间，分为4 个区间段，各区间所占比例如图1 所示。

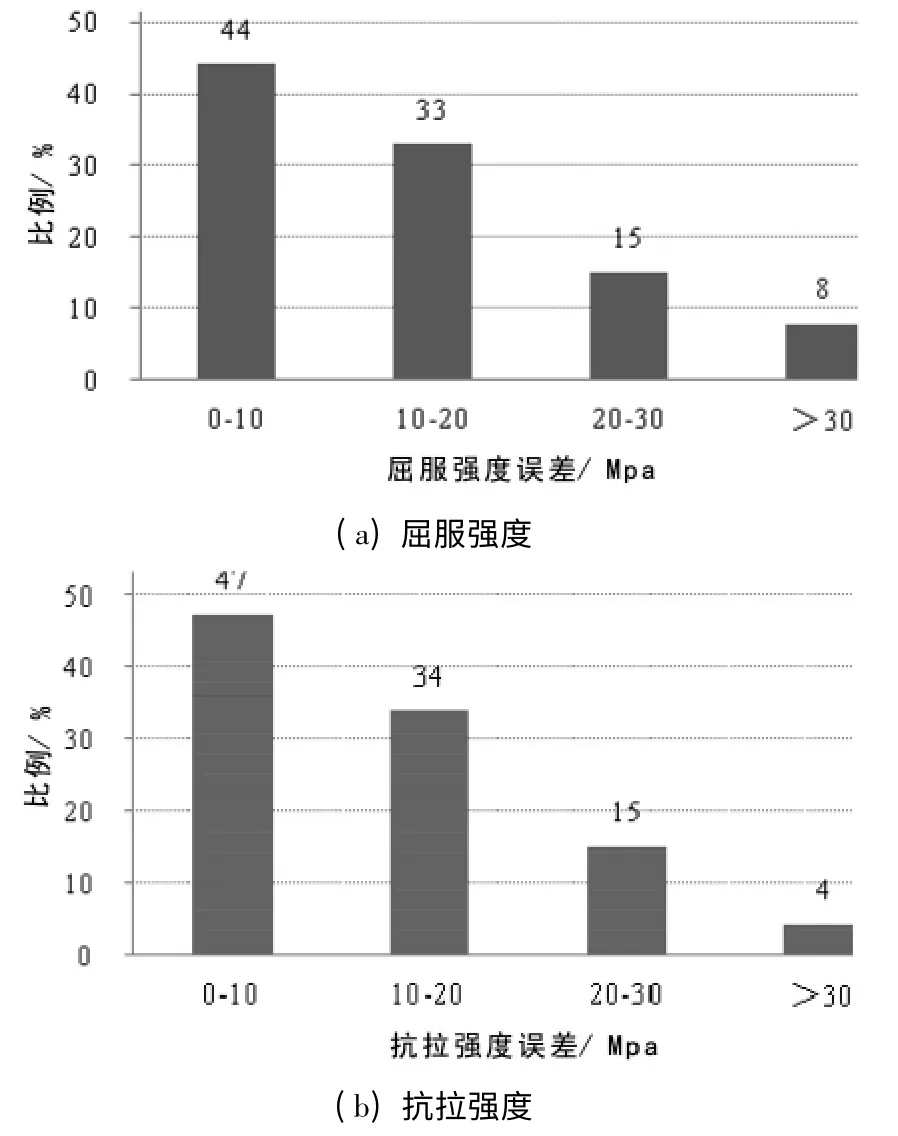
图1 性能实测值与回归方程计算值差值绝对值的区间所占比例

从图1 可以看出，屈服强度和抗拉强度在0 ～10 MPa 的误差分别为44% 和47%;在10 MPa ～20 MPa的误差分别为33% 和34%;在20 MPa ～30 MPa的误差都为15%;在30 MPa 以上的误差分别为8%和4%。抗拉强度在低误差范围所占比例比屈服强度高，在高误差范围所占比例比屈服强度低，再一次证明了抗拉强度的回归方程相关性比屈服强度好。

从回归方程对非样本数据进行验证的结果可知，虽然样本数据只有10 个规格，验证数据有21 个规格，但回归方程仍能够较好的得到验证，符合预测精度要求的比例都在90%以上，说明可以用回归方程作为现行生产工艺的指导方程，可为生产工艺、质量检验以及售后服务和质量异议提供参考和帮助。当然，由于数据存在误差，不可避免地出现回归精度的偏差，可根据实际生产需要，不断做出调整和改进，起到更好的预测作用。

回归方程是在符合表1 和表2 要求的范围之内回归所得到的，当变量取值超出此范围时，预测与实际之间的误差将会大幅增加，没有指导意义。若做出大的生产工艺调整，需相应地修正回归方程，才能保证高的吻合性和实时性。回归方程的研究要紧密联系生产实际，持续做出跟踪和研究，不断地修正系数，才能加以改进和完善［7］。

4 结论

1)在现有的生产工艺条件下，用逐步回归方法得到了低合金钢Q345B 化学成分及轧制规格与力学性能的回归方程。经检验，所有回归方程在α =0．05 水平上显著，通过复相关系数可知所有方程自变量与因变量的关系可信。

2)屈服强度和抗拉强度都随轧制规格增加而减小，随碳、硅、磷含量的增加而增加;碳、磷含量对抗拉强度的影响高于对屈服强度的影响;硅含量对二者的影响差别不大。

3)轧制规格对屈服强度影响比对抗拉强度影响大。

4)通过验证，100 个样本数据的回归方程的精度符合95%的误差不超过要求的范围，874 个验证数据用回归方程验证，误差在预测精度要求范围内的比例都在90%以上，说明可以用回归方程作为现行生产工艺的指导方程。

［1］余宗森，袁泽喜，李定秀，等．鞍钢钢材成分与其力学性能的定量关系［J］．北京科技大学学报，1997，19(5):510 －515．

［2］苏理云，邓燕，冉雪竹，等．低合金高强度钢力学性能与化学成分之间的统计建模与分析［J］． 重庆工学院学报(自然科学)，1999，23(2):36 －40．

［3］刘锋，唐华，苏理云，等．对低合金高强度钢力学性能与化学成分关系的一种统计分析［J］．重庆理工大学学报(自然科学)，2010，24(7):54 －59．

［4］张润生．多元回归分析在低合金钢板性能预测上的应用［J］．金属世界，2014(4):41 －43．

［5］刘宇雁，高箭宇，陈林，等．基于逐步回归法研究薄板钢化学成分与力学性能的关系［J］．包头钢铁学院学报，2006，25(1):18－21．

［6］余宗森，袁泽喜，刘锦标．韶钢钢材化学成分特点及其对力学性能的影响［J］．南方钢铁，2000(4):1 －6．

［7］杨敏，梁锡辉．冷轧SPCC 带钢化学成分和力学性能回归分析［J］．柳钢科技，2010，(4):16 －18．