用类比思维学习线段和角

□沈占立

用类比思维学习线段和角

□沈占立

传说鲁班的妻子看到一个小孩将一大片荷叶放在头上避雨，便心生灵感，类比发明了斗笠和雨伞.同样，线段和角也有很多类似的地方，同学们比对来学习，效果更好.

一、计数规律相同

1.线段的计数

线段的计数方法可采用“左端点顺次数线段法”，即将每个点作为左端点，顺次数出线段，再求和.如图1，以A点为左端点的线段有：AB、AC、AD；以B点为左端点的线段有：BC、BD；以C点为左端点的线段有：CD，共计线段的条数为3＋2＋1＝6.用此方法数不重不漏，是一种简单、快捷的方法.

一般地，当一条直线上有n个点或一条线段上有n个点（包括两个端点）时，可确定的线段条数为

图1

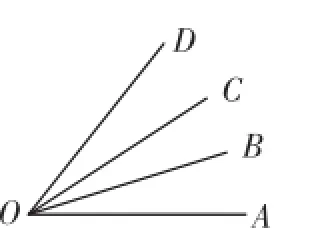
图2

2.角的计数

角的计数方法与线段的计数方法极其类似，可先以某一射线为始边，按一定的顺序数出角的个数，然后依次以后面的射线为始边数出角的个数，再求和.如图2，按逆时针方向，以OA为始边的角有∠AOB∠AOC、∠AOD；以OB为始边的角有∠BOC、∠BOD；以OC为始边的角有∠COD，角的个数共计为3＋2＋1＝6

一般地，从O点出发引出n条射线或一个角的内部有n－2条射线时，可确定的角的个数为

二、中间部分类似

1.线段中点间的距离

如图3，点P为线段AB上一点，D、E分别为线段AP、BP的中点. AB＝a，则有

证明：

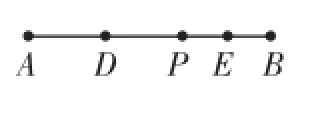
图3

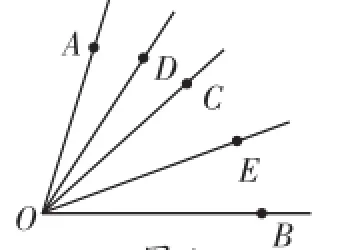
图4

2.角平分线间的夹角

如图4，OC是∠AOB内部的一条射线，OD、OE分别是∠AOC、∠COB的角平分线.则有

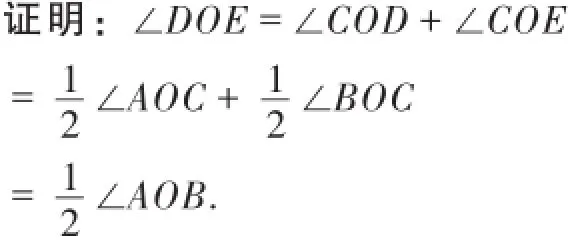
例1如图5，P为线段AB上任意一点，D为线段AP上靠近A点的三等分点，E为线段PB上靠近B点的三等分点，AB＝15，求DE长.

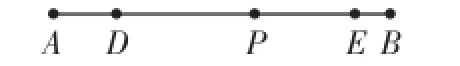
图5

分析：P是动点，所以不能分别求出DP、EP的值，需将DE转化成与已知线段AB相关联的量.DE＝点评：本题中线段的有关计算体现了整体的数学思想，这种思想在线段和角的计算中要经常用到，同学们要切实掌握.

例2从∠AOB的顶点O处引一条射线OC，OE、OF分别为∠AOC、∠COB的角平分线，∠AOB＝90°.

（1）如图6，射线OC在∠AOB内部时，求∠EOF的度数；

（2）射线OC在∠AOB外部时，如图7，求∠EOF的度数.

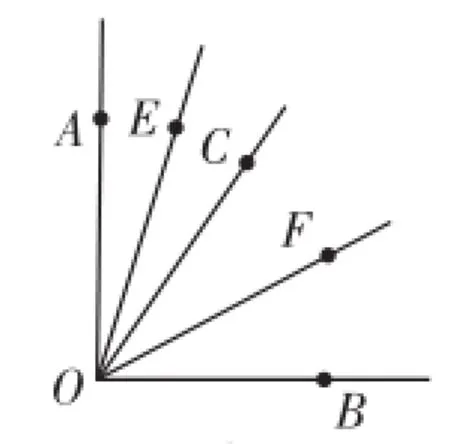
图6

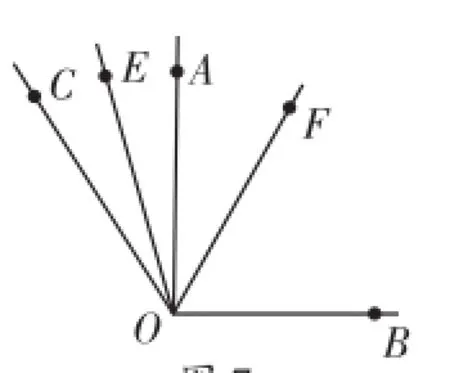
图7

分析：将∠EOF分割成∠EOC和∠FOC，再利用角平分线定义将它们与∠AOC、∠BOC联系起来.

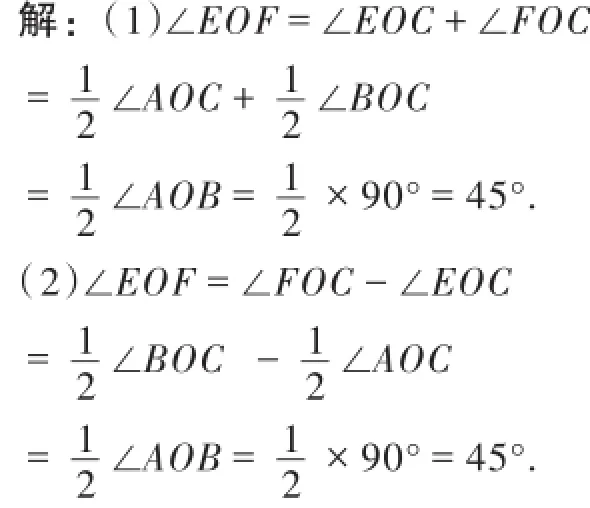
点评：本题中利用拆分、整合的思想是关键，先化整为零，再化零为整，目标明确向已知条件靠拢.