我国商业银行效率研究——基于交互评价的两阶段网络交叉效率模型

李双杰，张锦良

(北京工业大学经济与管理学院，北京，100124)

我国商业银行效率研究
——基于交互评价的两阶段网络交叉效率模型

李双杰，张锦良

(北京工业大学经济与管理学院，北京，100124)

已有“自评”两阶段网络DEA模型未能考虑其他决策单元指标权重取值情况，且存在权重向量非唯一的可能。文章对原有“自评”模型进行指标权重向量唯一化的二级规划，引入交叉效率的“自互评”模式构建了两阶段网络交叉效率模型，将商业银行运营过程分为以存款作为中间产出指标的两个相关联阶段，并对2009—2013年间我国16家上市商业银行进行了效率分析。结果显示，我国上市银行整体效率比较稳定，尚有较大提升空间，各类银行效率差异不大，且有趋同的趋势；盈利效率差异化不明显且变动平缓，吸储效率更能影响综合效率的结果。与“自评”模型相比，两阶段网络交叉效率模型评价客观，稳定性更强。

银行；指标；二级规划；两阶段网络DEA模型；交叉效率

一、引言及文献综述

银行业作为金融行业的支柱，在一国的经济活动中扮演着至关重要的角色。银行的经营效率是分析和评价银行经营状况的一个重要方面，效率的提高对于综合竞争力的提高有非常明显的作用。因此，如何对商业银行进行有效的效率评估，发现其不足，进而有针对性地提出改进方案，是非常有价值的。

包括银行业在内的很多生产体系都是一个网络架构，决策单元(DMU)的生产过程会分为一些子流程，一个子流程的产出可能会是下一个子流程的投入。传统DEA方法将生产过程看作一个“黑箱”，其测评过程不符合上述含有子流程的生产情况。为适用于这方面要求，Seiford和Zhu[1]将美国商业银行的生产过程分为盈利过程和产销过程两个阶段来测算效率，在测算过程中，其模型两个阶段之间并没有直接的关系，这使其在整体效率表示上缺乏说服力。Kao和Hwang[2]提出一种相关联的串式两阶段DEA模型，将保险公司的生产分为保险费获得和利润生产两个过程，并应用该模型对24家台湾非寿险保险公司进行了效率测算。两阶段网络DEA模型打开了DEA模型测算效率时的“黑箱”，更加贴近实际生产的情况，能够使银行效率评价更加系统。[3−7]然而，它存在指标权重分配极端、“自评价”不够客观公允的问题，交叉效率模型及其改进形式为上述问题提供了解决途径。Sexton等[8]于1986年首次提出了结合“自评”和“他评”过程的交叉效率方法，坚持了差异性、公平性原则，他们的方法弱化了经典DEA模型因自评乘子体系(指标权重)所导致的相对效率测度结论的极端性，对交叉效率的研究主要分为如何选择指标权重和如何求解交叉效率两个方面。对于第一个方面，很多研究选择了二级规划的方式对指标权重予以优化。[9−13]其中，又以解决权重向量的唯一性和减少零权重问题为焦点。[10,12]在另一方面，以加权法取代均值法来求解交叉效率则受到青睐。[14,15]

现阶段并没有文章从交叉效率角度对两阶段网络DEA模型进行优化，也没有文章使用交叉效率方法对国内银行进行效率研究，本文在这两方面做出尝试。

二、两阶段网络交叉效率模型的构建

图1所示为包含两个生产过程的串型网络生产示意图。在生产过程一中，由m项投入生产p项中间产出，全部中间产出作为生产过程二的投入参加过程二的生产并得到最终的s项产出，这样生产过程一与过程二通过中间产出产生了联系，最终整体效率是由m项投入得到s项产出的情况决定。

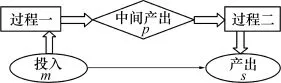
图1 两阶段生产过程的网络生产示意图

假设同一生产活动中有n个DMU，DMUj为(Xj、Zj、Yj)，其中Xj、Zj、Yj分别表示DMUj的投入、中间产出以及产出。假设投入项m种、产出项s种，中间产出项p种，则有Xj=(x1j，……，xmj)，Zj=(z1j，……，zpj) =(y1j，……，ysj)，j=1，2…n。对于决策单元DMUd，设vid为第i种投入的权重，tkd为第k种中间产出的权重，urd为第r种产出的权重。Ejd表示DMUd在DMUj权重体系下的“他评”效率值，Edd则为DMUd的“自评”效率值。

(一) 已有两阶段网络DEA模型

在两阶段DEA模型的应用中，周逢民等[3]借鉴了Kao和Hwang[2]的做法，得到如式(1)所示模型：

上述两阶段DEA模型并未考虑其他决策单元的指标权重情况，为传统的“自评”模式。模型(1)的综合效率值唯一，然而其两个子阶段效率值存在多解的可能。[2]为唯一确定两个子阶段效率值，Kao和Hwang[2]做了以第一阶段或第二阶段效率值最大为目标函数的二级规划，这实际上就人为地认为第一阶段效率值或第二阶段效率值更重要。这两种观点都显得偏颇。本文没有采用他们的做法，而是通过唯一化指标权重的二级规划达到只有一组解的目的。

(二) 交互评价的两阶段网络交叉效率模型构建

1. 构建二级规划模型确定唯一权重

商业银行的一些主要指标在各银行间的重要程度相似，为得到更加合理的效率值，最小化同一指标在不同决策单元间差异是可取的。在建立该部分模型时，我们将Jie Wu等[11]缩小目标决策单元内不同指标间差异的做法拓展到缩小同一指标在不同决策单元间的差异，在模型(1)的基础上进行了优化，得到模型(2)。由于目标函数是对指标权重的限制，模型(2)能够唯一确定目标单元的一组指标权重，从而能够唯一确定两个子阶段的效率值。

以上各值均大于等于零。

模型(2)中，αrd、βkd、γid分别表示决策单元d的产出指标r、中间产出指标k和投入指标i的加权值分别与产出、中间产出和投入在每个产出指标、中间产出指标以及每个投入指标上分配的均值间的差异，相应地，则表示上述差异在所有决策单元间的差异均值。

上面我们提到，“自互评”的交叉效率模式同时考虑了自身指标权重取值和其他决策单元的指标权重取值情况，相较于“自评”模式更加客观。所以，本文在模型(2)的求解过程中同时求得了在决策单元d的权重向量下，决策单元j的“他评”效率值，以便求解交叉效率。其中，Edj表示相应的综合“他评”效率值，E1dj表示相应的第一阶段“他评”效率值，E2dj则表示相应的第二阶段“他评”效率值。

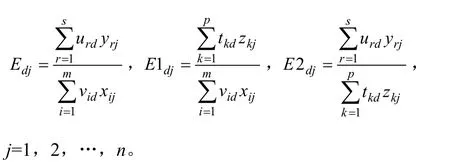
2. 构建两阶段交叉效率模型求加权交叉效率值

由上述模型所得各决策单元的“自评”效率值以及“他评”效率值可以组成效率矩阵。由于两阶段DEA模型能得到三个效率值，相应地会有三个效率矩阵，本文两阶段DEA模型算出的综合效率等于阶段一与阶段二效率值的积，然而由均值法求得的三个交叉效率值将不能保证上述乘积关系成立。本文以“最小化”上述关系的改变幅度为目标函数，同时对各决策单元赋权，求解加权交叉效率值。模型还加入了加权交叉效率值大于均值交叉效率值的限定，“自评”效率值是“利己”的，而算术均值是“自评”与“他评”同等重要下求得的交叉效率值。为体现公平性和差异性，较为科学的效率值应该介于两者之间。具体模型如下：

以上各值均大于等于零。

模型中，Eid、E1id、E2id分别表示决策单元d综合的、阶段一以及阶段二在决策单元i各指标权重下的他评效率值，Ed、E1d、E2d为综合的、阶段一以及阶段二的均值交叉效率值，则为相应的加权交叉效率值。得到如图2所示的效率矩阵后，均值交叉效率为加权交叉效率为=′dE第一阶段和第二阶段的两个交叉效率值与其表达形式相同。

图2 效率矩阵

三、我国银行效率实证

(一) 指标选择

在进行实证分析之前，能否对指标进行科学选取是本文研究的基础。在指标选取上，李双杰、高岩[16]认为，投入是指实物或服务的投入，应当是一个绝对值。银行生产的投入包括人力投入和非人力投入，员工费用相对于人员数量能从“量”和“质”两方面反映人力投入情况。非人力投入是指银行经营活动中投入的全部资产。银行业与制造业不同，固定资产在总资产中所占比例非常小，能够反映银行资产以及经营规模的资产类投入指标优先选择所有者权益。从盈利角度出发，实施单阶段效率测算时，投入指标中代表人力投入的员工费用包括已支付职工费用和应付职工薪酬两项；非人力投入包括负债合计−应付职工薪酬、股东权益两项，吸收存款及同业存放可作为负债合计代理变量(以2013年为例，我国16家上市银行吸收存款及同业存放占负债合计的比重基本都达到了9成左右，均值为89.61%)；产出指标选取净利润、所得税费用和营业税金及附加(也就是利税合计)。

商业银行生产过程存在明显的两阶段特点。第一阶段，商业银行利用人力投入和非人力投入来吸储。第二阶段则通过经营负债来获利。作为负债合计代理变量的吸收存款及同业存放在两个阶段中具有明显的衔接作用，并且与投入和产出指标的关联性很强。这点可以从后面的指标相关性分析中得到印证。由此，本文将存款及同业存放同时作为阶段一的产出指标和阶段二的投入指标，分两个过程来测算银行效率。本文银行效率评价指标如表1所示。

(二) 样本数据

对于银行样本，本文选择了最具代表性的我国16家上市商业银行2010—2013年的相应数据。2013年我国16家上市商业银行的资产合计和利润合计分别占银行业金融机构资产总额的62.86%和利润总额的82.27%，具有很高的代表性。从透明性上讲，由于每年上市公司都要披露年报，其信息开放，数据可得性和准确性高。鉴于我国上市商业银行的规模及特点，一般将其分为三类：国有商业银行、股份制商业银行以及城市商业银行。

表1 银行效率测算指标

本文数据主要来自国泰安CSMAR系列研究数据库，不足或空缺的数据由上市银行相应年度年报填补。统计性描述如表2所示。

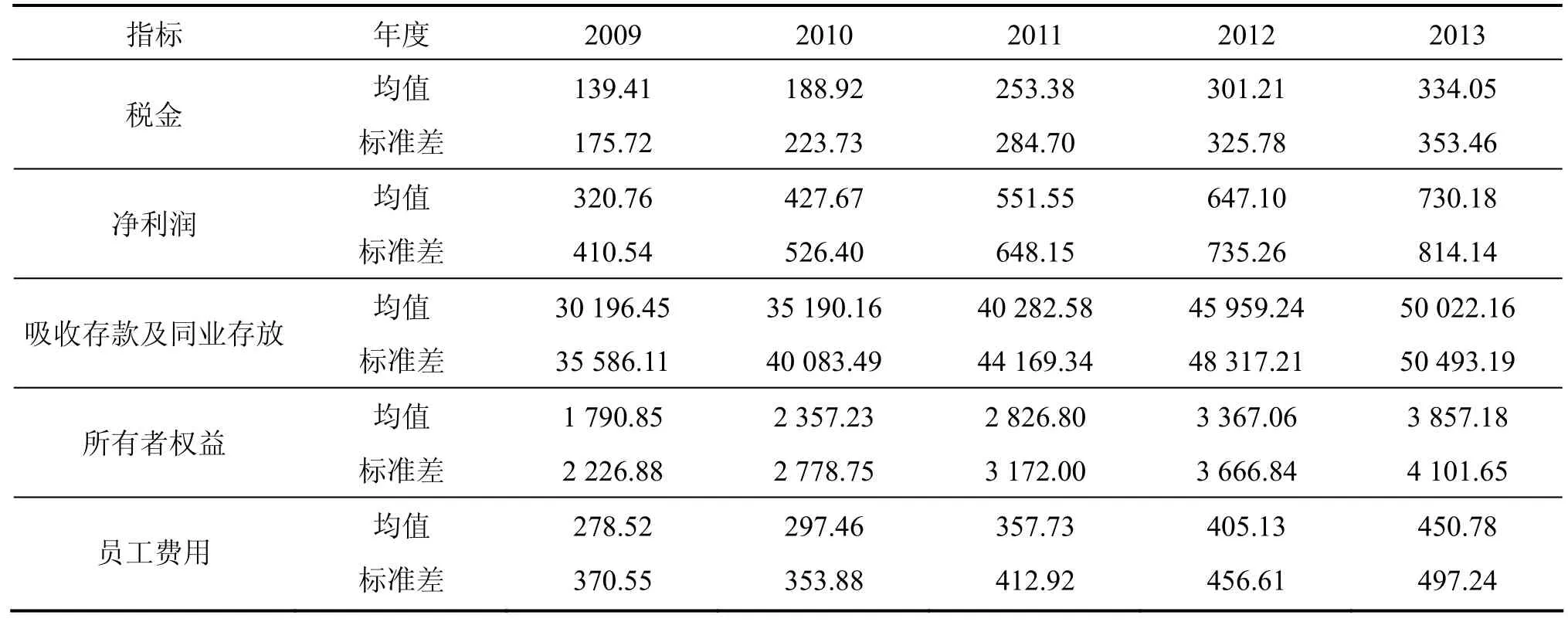
表2 银行效率测算指标数据描述性统计(单位：亿元)

Lang、Golden[17]曾指出投入产出指标的选取须符合相关性检验：其相关系数愈高，相关程度愈大，这样能够确保投入与产出指标间具有因果关系，评价结果更可靠。相关性检验结果如表3所示：各投入项与各产出项之间高度正相关，相关系数都在0.9以上，这表示投入增加时，产出亦随之增加，符合DEA模型的同向性要求。本文所选指标数为5，生产单元数为16，符合Charnes经验公式n＞=2(m+s)，其中m和s分别表示投入、产出指标数，n代表生产单元数；产出指标与投入指标间没有直接的线性关系，这点可由相关性检验结果证实。综上，本文所选指标符合DEA方法对指标选择的要求，所选指标是合理的。

(三) 两阶段交叉效率模型结果及分析

1. 综合技术效率测算分析

在上述样本数据及指标选择的情况下，应用本文构建的两阶段网络交叉效率模型对2009—2013年间我国16家上市商业银行进行效率测算的结果如表4所示。

根据2009—2013年效率结果，我国上市商业银行的整体综合效率值有较大提升空间，5年的效率均值基本都在0.6～0.7之间。所有银行在2010年效率值最低，一种可能的解释为金融危机的负面影响在2010年达到了最大。总体效率均值在2011年最高，之后开始小幅下滑。三类银行中，股份制银行历年效率均值最高；城市银行的效率均值在2009年高于国有银行，2010年起每年效率均值都为最低；国有银行的效率均值处于中间位置；三类银行效率均值在2013年变得非常接近，不同类别银行效率有趋同的趋势 (图3)。各类银行效率均值波动不大。

由表4可见，兴业银行、工商银行、民生银行和北京银行4家银行5年效率均值分列第1到第4名，中国银行、平安银行、南京银行和农业银行4家银行效率表现较差。农业银行在2009年的效率值最差，仅为0.335 4，比规模相近的中国银行低了近一倍。分析其投入产出数据，农业银行该年度投入指标中，员工费用超过1 239亿元，超出中国银行近一倍，然而其净利润和税金分别约为650亿元和215亿元，中国银行这两个产出分别约为853亿元和374亿元。至此，我们可以大体了解农业银行在2009年效率值过低的原因：在产出不高的情况下，其员工费用的相对投入远远高于其他银行。平安银行整体效率表现较差，值得一提的是平安银行在2009年的效率表现在16家上市银行中处于上游，2010年后其效率值骤降，一度处于最末两位。这与2010年平安集团收购深圳发展银行，两家银行整合过程中所带来的效率上的负面影响有关。George E. Halkos等[18]的研究结果也支持了这一现象，他们对银行并购的研究结果显示，原来的效率银行并购后将不能确保其仍是有效率的。国有银行中，工商银行效率值突出，中国银行与农业银行表现较差，且农业银行波动性较大；股份制银行中，兴业、民生、招商整体表现不俗，华夏、中信、平安有待提高；城市银行5年整体效率均值较差，但北京银行表现较为突出。不难发现，效率表现好的银行一般都具有认可度较高、盈利性较好、整体实力较强的特点。

表3 2009—2013年指标数据相关性分析结果

表4 2009—2013年两阶段综合交叉效率结果

从对综合效率的整体分析我们得出：我国上市商业银行在2009—2013年间整体效率水平有待提高；金融危机对三类银行的冲击都比较明显，各类银行在抗风险和抵御外界冲击的能力上需要加强；股份制银行效率最高，这说明股份制经营模式仍然具有相对优越性；不同类别银行之间的差距有逐步缩小的趋势。个体分析结果显示，国有银行在精简人员和优化人员结构上亟待加强，商业银行效率表现与其整体竞争力具有一定正向相关性。

2. 两个阶段技术效率测算分析

本文模型涉及两个相关联阶段，两阶段的效率值在一定程度上分别反映银行的吸储能力和盈利能力。

由表5可知，在第一阶段，股份制银行效率均值最高，随后的国有银行效率均值低了超过0.08个效率值，城市银行略低于国有银行；第二阶段的情况与第一阶段几乎相反，国有银行效率均值稍高于城市银行，成为效率均值最高的一类，股份制银行排在最后。

图3所示为银行综合效率以及两个阶段效率均值的趋势图。第一阶段的效率趋势与综合效率趋势大体一致。城市银行在2010年略微下降，之后则呈现加速上升的趋势；总体均值、国有银行均值及股份制银行均值在2010年后开始上升，在2013年呈下降趋势(国有银行在2012年就开始下降)。第二阶段的效率值变化幅度相对较小，城市银行整体呈下降趋势，并在2010年和2013年出现两次大幅度下滑；国有银行和股份制银行小幅度上下波动。由此可见，综合效率的变化趋势更多是受到第一阶段效率变化的影响。

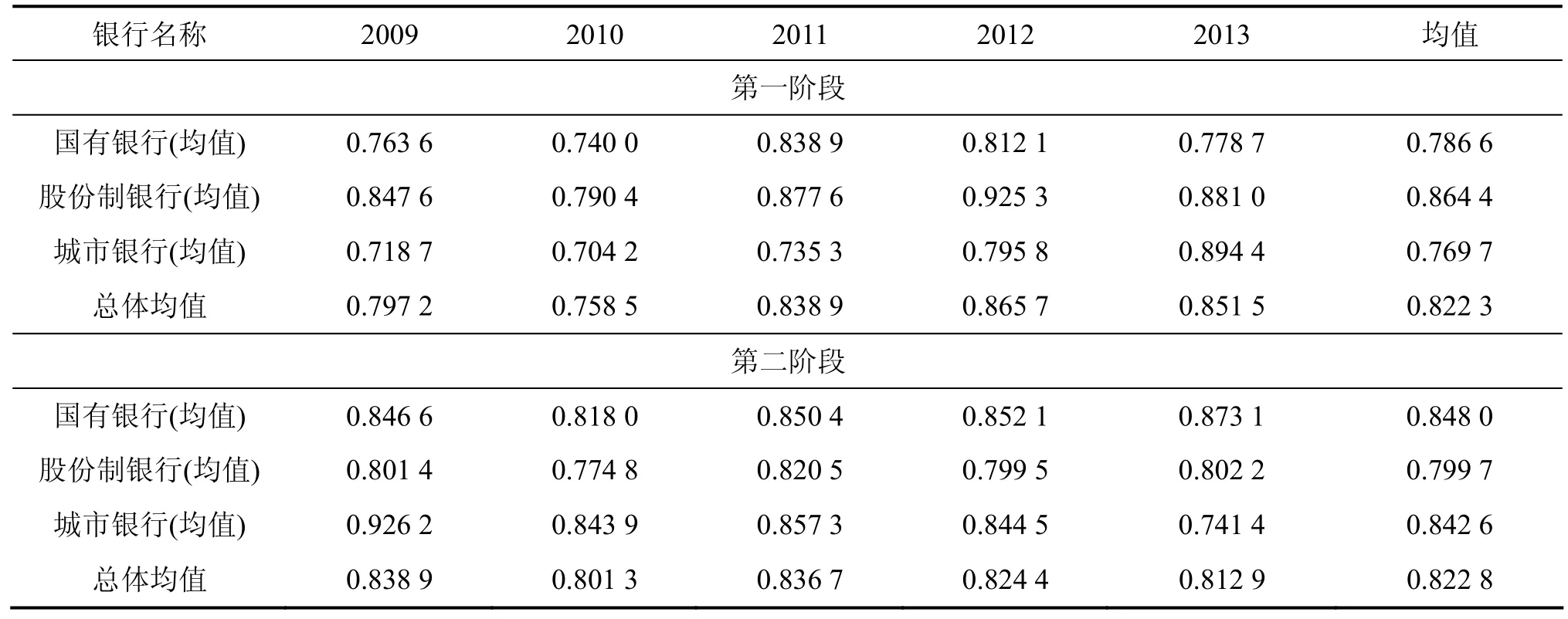
表5 2009—2013年两个阶段交叉效率结果

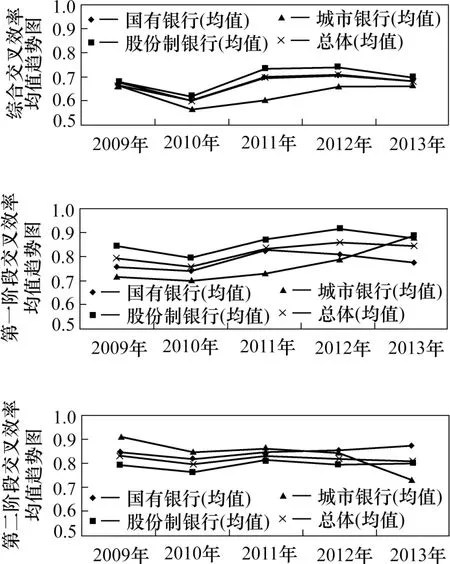
图3 各类银行交叉效率均值趋势图

由图4可知，总体的效率均值在第一阶段和第二阶段几乎相等。这说明对整体来讲，第一阶段与第二阶段的效率表现或者说对综合效率的贡献大致相同，然而不同类型银行两个阶段的效率表现却有较大的差距。三类银行相比，第二阶段的影响对国有银行和城市银行的综合效率产生了拉动作用，抑制了股份制银行的综合效率表现；第一阶段的影响与之相反。

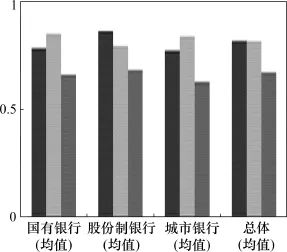
图4 各类银行交叉效率均值不同阶段对比图

结合前面的分析，股份制银行吸储效率更优，国有银行和城市银行盈利效率较高。国有银行和股份制银行与整体一致，在2013年，吸储效率相对减弱，盈利效率开始增强；城市银行吸储效率提升明显，盈利效率却出现相对下滑的迹象。由第一阶段效率和整体效率趋势的相对一致性可见，总体上我国商业银行效率变化主要受吸储效率的影响。第二阶段的盈利效率差异化不明显且变动相对平缓。我国商业银行凭借其在国内金融业的垄断地位，有着非常便利的吸收存款条件，它们所参与的盈利性金融活动量很大，但是种类较为单一，创新性较差，对传统业务的经营不容易使银行间在盈利效率上拉开差距。我国的银行业虽然经历了商业化和股份制改革，但并没有完全市场化，政策性影响很明显，这对银行的效率表现会有较大程度的影响。这也能在一定程度上解释为什么不同类别银行间两个阶段效率表现会出现上述的差异性。

(四) 两种模型的比较分析

本文在对2009—2013年我国16家商业银行进行效率测算时，还应用两阶段网络DEA方法(接下来称其为方法一，本文模型称为方法二)在本文指标体系及数据选取的基础上对2009—2013年我国16家商业银行进行了效率测算，其结果具有可比性。

1. 两种方法的测算结果比较

由表6可见，方法一的效率值高于在其基础上“自互评”的方法二效率值。方法一和方法二的相对结果具有较高的一致性，三类银行的效率均值由高到低依次为：股份制银行＞国有银行＞城市银行。

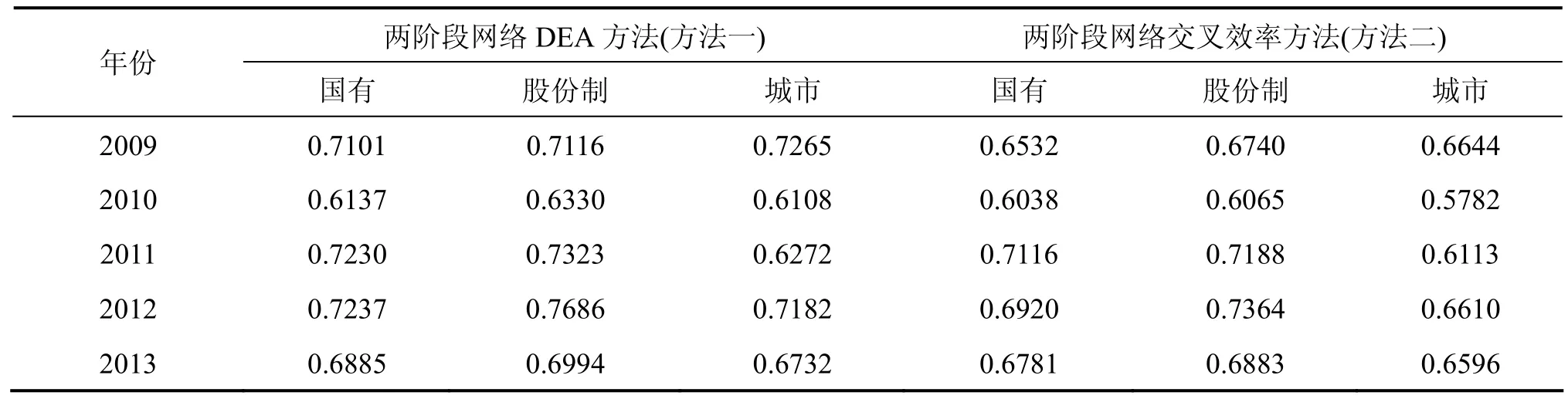
表6 三类银行不同方法效率均值结果

对方法一与方法二下不同银行的5年效率均值进行Mann-Whitney检验，p-值为0.220 6，接受原假设，说明两个方法的结果存在差异，但大体一致。

2. 两种方法的比较分析

用传统DEA模型进行效率测算时，其单一阶段的评价结构比相同指标体系下两阶段结构的方法一限制性要弱，其结果可能会高估评价单元的效率值。[7]方法一相对于单阶段DEA模型的优势在于：其一，两阶段模式更加符合商业银行的生产经营特点；其二，传统DEA模型容易出现多个效率单元，对于参评单位的区分度较低，而相关联两阶段的效率测算结构对测算更加细化，每一阶段效率值的差异都会对最终效率值有直接影响，这就加强了不同单位间的区分性。方法二与方法一相比，其最大的优势在于采用了“自互评”模式。在进行效率评价时，方法二会综合考虑其他决策单元的情况，评价更加客观。在方法一和方法二的测算结果中，中国农业银行在方法二下的排名相对于方法一有所下降(2013年效率排名下降两位，2009—2013年的效率均值下降一位)，这说明引入“自互评”后，不利于其在整体中的排名。这揭示了“自评”情况下其权重赋值相对极端，在其他决策单元中“得不到认可”，引入“他评”效率对其影响更大。

方法二还以不同决策单元间“指标加权值”差异最小为目标进行了二级规划。如表7所示，二级规划后，权重赋值发生变化的中国银行和北京银行分别减少了一个零权重；权重赋值朝着目标函数的限定方向变化。权重限定后，原先的零权重消失了，这说明决策单元能够得到“自评”效率值的权重体系并不是唯一的，在目标函数的限定下，模型选择了不含零权重的权重体系。该方法在达到了目标函数效果的同时兼顾指标权重不唯一问题，增强了解的稳定性(解唯一)，并且能够有效减少零权重的出现。

表7 2013年指标权重限定前后权重发生变化银行的赋权情况

四、结语

在已有方法的基础上，本文将交叉效率评价中的“自互评”模式引入到两阶段关联DEA方法中，通过二级规划对模型进行指标权重向量唯一化的优化，构建出本文银行效率测算模型。与“自评”两阶段关联DEA方法相比，本文模型引入了交叉效率评价中的“自互评”模式，评价结果兼顾公平性与差异性。另外，本文模型对指标权重进行了优化，并对各决策单元赋权，得到加权交叉效率值，增强了解的稳定性。

本文应用两阶段交叉效率模型对我国16家上市商业银行进行效率测算的结果显示：我国商业银行整体效率波动性不大，有较大提升空间；股份制银行效率较高，但各类银行效率差异并不明显，且有趋同的趋势。商业银行效率表现与其整体竞争力具有一定正向相关性。股份制银行的相对高效率说明了国有银行股份制改革的可取性，国有银行规模管理及体制上有待改善。我国城市商业银行起步较晚，提升空间较大。金融危机对三类银行的冲击都比较明显，各类银行在抗风险和抵御外界冲击能力上需要加强。

银行生产经营过程分为两个阶段：第一阶段主要目的为吸储，第二阶段则在吸收存款的基础上盈利。股份制银行吸储效率更优，国有银行和城市银行盈利效率较高。总体上，我国商业银行效率变化主要受吸储效率的左右，盈利效率差异化不明显且变动较平缓。因此，加强金融创新以增加产品多样性；鼓励竞争以加强银行业盈利能力；深化改革，逐步弱化政策性偏倚和地方保护主义，提升公平性以改善市场环境；这些措施都有助于我国商业银行竞争力的提高。

[1] Seiford L M, Zhu J. Profitability and marketability of the top 55 US commercial banks [J]. Management Science, 1999(45): 1270−1288.

[2] Kao C, Hwang S-N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan [J]. European Journal of Operational Research, 2008, 185(1): 418−429.

[3] 周逢民, 张会元, 周海, 等. 基于两阶段关联DEA模型的我国商业银行效率评价[J]. 金融研究, 2010(11): 169−179.

[4] 芦锋, 刘维奇, 史金凤. 我国商业银行效率研究−基于储蓄新视角下的网络DEA方法[J]. 中国软科学, 2012(2): 174−184.

[5] Hirofumi Fukuyama S M. Mirdehghan. Identifying the efficiency status in network DEA [J]. European Journal of Operational Research, 2012(220): 85−92.

[6] Peter Wanke, Carlos Barros. Two-stage DEA: an application to major brazilian banks [J]. Expert Systems with Applications, 2014(41): 2337−2344.

[7] Wang Ke, Huang Wei, Wu Jie, et al. Efficiency measures of the Chinese commercial banking system using an additive two-stage DEA [J]. Omega, 2014(44): 5−20.

[8] Sexton T R, Silkman R H, Hogan A J. Data envelopment analysis: critique and extensions[C]// Silkman R H (ed.). Measuring Efficiency: an Assessment of Data Envelopment Analysis. Jossey-Bass, San Francisco, 1986: 73−105.

[9] Wang Yingming, Chin Kwaisang. A neutral DEA model for cross-efficiency evaluation and its extension [J]. Expert Systems with Applications, 2010(37): 3666−3675.

[10] Wang Yingming, Chin Kwaisang, Jiang Peng. Weight determination in the cross-efficiency evaluation [J]. Computers & Industrial Engineering, 2011(61): 497−502.

[11] Wu Jie, Sun Jiasen, Liang Liang. Cross efficiency evaluation method based on weight-balanced data envelopment analysis model [J]. Computers & Industrial Engineering, 2012(63): 513−519.

[12] Nuria Ramón, José L. Ruiz, Inmaculada Sirvent. On the choice of weights profiles in cross-efficiency evaluations, on the choice of weights profiles in cross-efficiency evaluations [J]. European Journal of Operational Research, 2010(207): 1564−1572.

[13] Nuria Ramón, Jose´ L. Ruiz, Inmaculada Sirvent. Reducing differences between profiles of weights: a “peer-restricted”cross-efficiency evaluation [J]. Omega, 2011(39): 634−641.

[14] Wu Jie, Liang Liang, Yang Feng. Determination of the weights for the ultimate cross efficiency using shapley value in cooperative game [J]. Expert Systems with Applications, 2009(36): 872−876.

[15] Wu Jie, Sun Jiasen, Liang Liang, et al. Determination of weights for ultimate cross efficiency using shannon entropy [J]. Expert Systems with Applications, 2011(38): 5162−5165.

[16] 李双杰, 高岩. 银行效率实证研究的投入产出指标选择[J].数量经济技术经济研究, 2014(4): 130−144.

[17] Lang James R, Golden, Peggy A. Evaluating the efficiency of SBDC with data envelopment analysis: A longitudinal approach [J]. Journal of Small Business Management, 1989(27): 42−49.

[18] Georgios E. Chortareas, Jesús G. Garza-García, Claudia Girardone. Competition, efficiency and interest rate margins in latin american banking [J]. International Review of Financial Analysis, 2012(24): 93−103.

Research on the efficiency of Chinese commercial banks: through interactively-evaluated two-stage network cross efficiency model

LI Shuangjie, ZHANG Jinliang
(School of Economics and Management, Beijing University of Technology, Beijing 100124, China)

The existing “self-evaluation” two-stage network DEA model has not considered the indicator weight values of other decision-making units, and is not likely to be the only weight vector. This article implements the secondary planning which makes the indicator weight vector the only one, and introduces the “self-mutual evaluation” model of cross efficiency to construct the two-stage network cross efficiency model. And then, with the process of bank efficiency evaluation being divided into two related phases with the deposit being an intermediate output indicator, the article studies efficiencies of the 16 listed commercial banks in China from 2009 to 2013. Results show that the efficiencies of listed commercial banks in China as a whole is stable and has large room to be improved. The differences of efficiencies between all kinds of banks are not obvious, and these banks have the tendency of convergence. Their profit efficiencies level off without obvious differences, and the efficiency to absorb funds at the first stage can better control the banks’ synthesis efficiency. Compared with the previous “self-evaluation” model, this two-stage network cross efficiency model can evaluate more objectively with stronger stability.

bank; indicator; the secondary planning; two-stage network DEA model; cross efficiency

F832.4

A

1672-3104(2015)03−0130−08

[编辑: 苏慧]

2014−12−04；

2015−03−27

北京市社科基金重点项目“北京地区理工科高校科研竞争力分析”(12JGA005)

李双杰(1963−)，男，河北保定人，博士，北京工业大学经济与管理学院教授，博士生导师，主要研究方向：经济计量模型，(金融)企业绩效与效率分析；张锦良(1988−)，男，河北任丘人，北京工业大学经济与管理学院硕士研究生，主要研究方向：数量经济学