中国股市长记忆性与趋势变化研究

张金凤+马薇

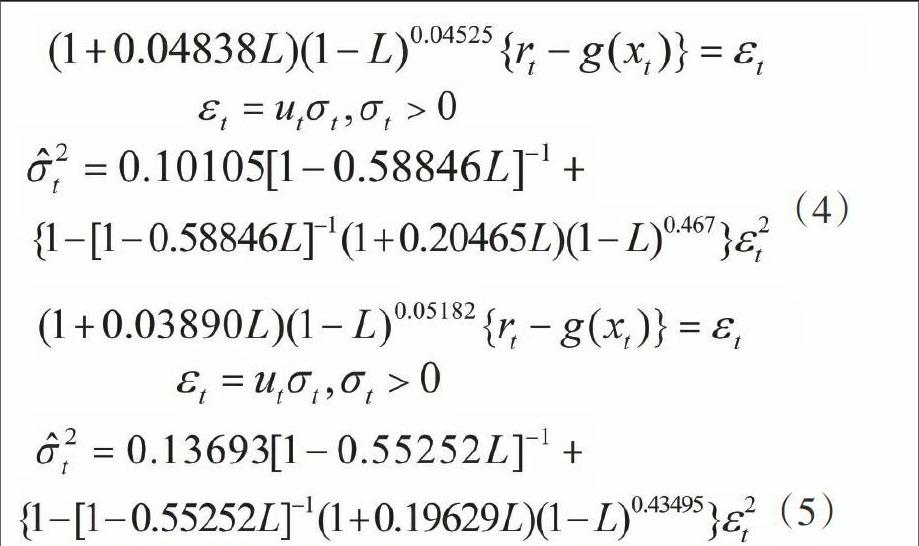
摘 要：文章对中国股市的长记忆性进行研究，在研究中将SEMIFAR模型与FIGARCH模型相结合，建立了既能反映收益率趋势变化情况又能描述收益率和波动长记忆特征的SEMIFAR-FIGARCH模型，利用该模型对我国沪、深两市的收益率和波动率的长记忆性及趋势变化进行实证分析，并与ARFIMA-FIGARCH、ARFIMA-HYGARCH模型结果比较拟合及预测效果。研究结果表明：我国沪、深两市的收益率和波动率均存在长记忆性；其收益率序列存在显著的趋势变化特征；SEMIFAR-FIGARCH模型的拟合和预测效果优于ARFIMA-FIGARCH、ARFIMA-HYGARCH模型，表明SEMIFAR-FIGARCH模型对我国股市有较好的模型解释能力和预测能力。

关键词：SEMIFAR-FIGARCH模型；趋势；长记忆；核估计方法

作者简介：张金凤，女，天津财经大学博士研究生，天津工业大学理学院教师，从事非参数计量经济学研究；马薇，女，天津财经大学理学院博士生导师，从事非参数非线性计量经济学研究。

基金项目：全国统计科学研究项目“大数据条件下金融风险测度的方法研究”，项目编号：2014LY003

中图分类号：F830.91 文献标识码：A 文章编号：1000-7504（2015）06-0055-07

金融时间序列的长记忆性也称为长期相关性，描述了金融时间序列中相距较远的观测值之间稳定的依存关系。Mandelbrot最早提出了长记忆性的概念，并将其应用在资产收益的研究中，此后，在金融领域长记忆性得到广泛的应用。对金融时间序列而言，具有长记忆性意味着过去会持续影响着未来。如果金融时间序列存在长记忆性，一方面基于布朗运动和鞅过程假设所导出的金融衍生产品定价模型将失效，金融市场会面临较大的风险；另一方面长记忆性的存在可为金融资产的预测提供一定的理论支撑。因此，关于金融时间序列长记忆性的检验与研究，逐渐成为近年来金融领域研究的一个热点和重点问题，特别对金融市场的风险控制、价格预测、市场监管等方面都有着重要的理论意义与应用价值。

目前关于金融时间序列长记忆性的检验与研究主要有统计方法和模型方法两大类。从20世纪80年代以来，国内外学者关于长记忆性进行了大量实证研究。Greene和Fielitz（1977）[1]，Barkoulas、Baum和Travos（2000）[2]，Sibbertson（2004）[3]通过R/S检验表明美国、希腊、德国等国家的股票收益率存在明显的长记忆性；王春峰、张庆翠和李刚（2003）[4]利用R/S方法对我国1993—2001年间沪、深两市的长记忆性进行检验，得出我国股票市场存在较强的长记忆性，不是一个效率市场；张维和黄兴（2001）[5]检验出中国股市日、周收益率均存在长记忆特征，市场呈非线性的波动。在模型方法上，Granger和Joyeux（1980）[6]，Hosking（1981）[7]提出了能够较好描述金融时间序列持续性和长记忆性的ARFIMA模型，并广泛应用在经济金融领域中。对金融时间序列的波动情况，目前多采用GARCH模型族如FIGARCH模型和HYGARCH模型来刻画其长记忆性。一些学者还尝试将ARFIMA模型与FIGARCH、HYGARCH模型分别结合，构造出ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型来同时考察金融时间序列收益率和波动的双长期记忆程度，如Kang和Yoon（2006）[8]利用上述模型分析了日本、韩国、新加坡以及中国香港的股票市场，得出这些股市的收益率不存在长记忆性，而波动存在长记忆性和非对称性；张卫国、胡彦梅和陈建忠（2006）[9]，曹广喜（2009）[10]，石泽龙和程岩（2013）[11]分别对我国股市及亚洲汇率市场建立了ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型来检验金融市场收益率和波动率的双长期记忆特征。此外不断有学者对上述长记忆研究的模型方法进行改进与扩展，以达到更好地分析和预测效果。Beran和Ocker（1999）[12]对ARFIMA模型进行扩展，将模型中的常数项替换成平滑趋势函数，进而提出了SEMIFAR（semiparametric fractional autoregressive model）模型。SEMIFAR模型在考察金融时间序列长、短记忆特征的同时，还可以通过平滑趋势函数分析收益的趋势变化，一般情况下，趋势可分为确定性趋势和随机性趋势两种，因此SEMIFAR模型能较好地捕捉到任何一种趋势的变化。随后，Beran和Feng（2002）[13]系统地总结了SEMIFAR模型的估计方法，简单地讨论了模型的预测能力，并指出SEMIFAR模型要比一般的平稳长记忆模型更强大。Feng、Beran和Keming（2007）[14]，Chikhi、Peguin-Feissolle和Terraza（2013）[15]分别将SEMIFAR模型应用到各种实际分析如汇率、股市中，发现该模型有较强的解释能力。国内应用SEMIFAR模型的文献还很少，陈秋雨（2011）[16]通过SEMIFAR模型研究了中国黄金期货市场，发现其收益率存在很强的长记忆性，并指出长记忆中大部分由确定性趋势来把握，随机性趋势则接近随机游走过程；郑雪峰和陈铭新（2012）[17]对深圳成指1997—2011年收益率建立SEMIFAR模型，得出深圳成指收益存在长记忆性，其趋势变化是先降再升，其后又下降的态势，并进行了相应的预测，得到较好的结果。

通过对文献的梳理，发现国内关于SEMIFAR模型主要集中在金融资产收益率的长记忆性与趋势变化的研究，而同时考察收益率和波动长记忆性的SEMIFAR模型还没有做更深入的探讨。因此，本文将SEMIFAR模型与FIGARCH模型结合，构成SEMIFAR-FIGARCH模型对中国股市进行实证研究，同时为了比较模型拟合和预测效果，与ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型进行对比分析。本文通过实证分析考察SEMIFAR-FIGARCH模型在拟合数据、预测效果方面是否优于ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型，在这过程中还研究了中国股市是否存在明显的趋势变化情况。

一、模型设定与改进

（一）SEMIFAR-FIGARCH模型

Beran提出的SEMIFAR模型，既考虑了金融时间序列的短期和长期记忆特征，又能把隐藏在确定性趋势背后的随机性趋势挖掘出来，可见，SEMIFAR模型是研究金融时间序列趋势变化成因的一个有力工具。此外为了更好刻画金融资产波动率的长记忆性，Baillie、Bollerslev和Mikkelsen（1996）用（1-L）s代替IGARCH模型的一阶差分算子从而提出了FIGARCH模型。在实际中，金融时间序列的收益率和波动率大多存在长记忆性，因此本文将SEMIFAR模型与FIGARCH模型相结合得到SEMIFAR-FIGARCH模型，该模型不仅能同时考察金融资产收益率和波动率的长记忆性，还能刻画收益率的趋势变化组成情况，这是以往长记忆模型所不能提供的。

设时间序列 ，则SEMIFAR（p，δ）-FIGARCH（r，s，n）模型形式如下：

（1）

正整数m∈{0，1}，?（L）、α（L）和β（L）分别是滞后算子L的p阶、r阶和n阶多项式。（1-L）δ的二项展开式为：

（2）

是gamma函数， 。（1-L）δ的二项展开式同（2）式。参数p描述了序列{Yt}的短期记忆程度，分整参数δ∈（-0.5，0.5）刻画了序列{Yt}的记忆程度，当δ∈（0，0.5）时，序列{Yt}具有长记忆特征；当δ∈（-0.5，0）时，序列{Yt}具有反持续性；当δ=0时，序列{Yt}具有短期记忆性。由于许多金融资产都可通过至多一次差分实现平稳，因此正整数m的取值为0或者1，是时间序列{Yt}差分到平稳的次数，m=0时，Yt=g（xt）+ξt；m=1时，（1-L）Yt=g（xt）+ξt，显然?（L）（1-L）δξt=εt就是一个q=0的ARFIMA（p，δ，0）过程，是一个平滑趋势函数，刻画序列的趋势变化，一般采用非参数核估计法估计。波动率方程中其中w为常数项，参数s刻画了FIGARCH过程的长期记忆特征且0

从模型的形式可以看出，由于平滑趋势函数的引入，使得SEMIFAR模型更加灵活，应用也更广泛。同时也注意到，SEMIFAR模型并不包含移动平均过程MA项，也就是剔除了随机扰动项前期累计影响，充分体现了当前数据的变化特征。

（二）SEMIFAR-FIGARCH模型估计方法

为了估计SEMIFAR-FIGARCH模型中的参数，不妨令 是估计过程中SEMIFAR部分的参数向量，

是FIGARCH部分的参数向量， 、

是对应的参数估计向量，则SEMIFAR-FIGARCH模型中的参数可用三阶段法估计：首先利用非参数方法估计趋势项函数 ，然后估计SEMIFAR部分的参数向量 ，最后估计FIGARCH模型的参数向量 。

二、对我国股市长记忆性的实证研究

接下来利用上面改进的SEMIFAR-FIGARCH模型对我国股市收益率和波动率的长记忆性和趋势变化情况进行分析与研究。

（一）变量选取与数据分析

为了更好地反映我国股市的变化特征，本文选取上证综指和深圳成指在t日的收益率作为研究变量记作，Rti（i=1，2），这里收益率序列采用对数差分形式=100ln（Pti / Pt-1i），其中Pti（i=1，2）是沪深两市在t日的收盘指数。根据经济形势变化的特点，选取数据样本区间从1997年1月2日至2014年5月15日，各有4197个收益率数据包含了我国股市上涨、下跌以及调整的全过程。为了对SEMIFAR-FIGARCH模型和ARFIMA-FIGARCH模型、ARFIMA-HYGARCH模型的拟合及预测效果进行评价和比较，将1997年1月2日至2013年4月30日共3955个样本数据作为上述模型的估计样本来进行建模与分析，其余242个样本数据用于模型预测波动性能力的评价。所有实证分析过程采用S-PLUS8.0和OxMetrics6.0软件操作，数据来源于Wind股票交易系统。

1. 基本统计分析

表1（见下页）列出了样本估计期内上证综指和深圳成指的收益率序列基本统计特征。从表1所示数据可以看到，沪、深两市收益率均值较小，偏度均为负，同时峰度值均超过正态分布的峰度值3，表明两市收益率都具有左偏、尖峰厚尾的特征，均不服从正态分布，这也可从J.B统计量及相应的P值得出相同的结论；单位根ADF检验结果表明沪、深两市收益率均为平稳序列；两指数的ARCH检验统计量在5%显著性水平下均拒绝了序列不存在异方差的零假设，即沪、深两市收益率序列存在着ARCH效应，适合建立GARCH模型。这点从图1也可以看出，沪、深两市收益率序列存在较强的波动集聚性及持续性，且波动的集聚性相似。

2. 独立性检验

表2（见下页）给出了沪、深两市收益率的独立性检验的情况：在5%的显著性水平下，两股指的BDS统计量均大于标准正态分布的临界值1.96，因此拒绝沪、深股市收益率序列独立同分布的零假设。由检验结果可以看出，中国股市的变化规律很难确定，股市存在相应的风险。

（二）长记忆检验

由于金融市场大多呈现出一定的记忆性，因此，有必要检验沪、深两市收益率和波动率是否存在长记忆性。这里采取GPH谱回归法，是由Geweke和Porter-Hudak（1983）提出的一种半参数长记忆检验方法。时间序列{Yt}的分整谱密度为： ，其中w是傅里叶频数，fu（w）是相对于ut的谱密度。为了求d，对上式取对数得

（3）

在大样本且 情况下， 。参数可用最小二乘法估计，这里U是Uj的样本均值。GPH谱回归法能直接给出分整参数d的估计值，而d与Hurst指数（H）之间的关系为H=d+0.5。Hurst指数包含了全部变动区间，当-0.5

综合以上的检验结果，沪、深股市收益率序列是平稳的，存在ARCH效应，且收益率和波动率均存在长记忆性，具有一定的可预测性，因此对沪、深指数收益率和波动率序列采用SEMIFAR-FIGARCH模型来建模，其中均值方程为SEMIFAR模型，方差方程为FIGARCH模型。

（三）模型估计结果及分析

本文首先采用极大似然估计法对SEMIFAR模型进行估计，由于沪、深两市的收益率序列均是平稳的，故两指数SEMIFAR模型的差分参数m均取零，而滞后阶数p则是从0到5的整数中进行选择并根据信息准则BIC值最小来确定其取值，估计结果表明：沪、深两市的SEMIFAR模型滞后阶数p均为零即收益率不存在短期记忆特征；沪、深两市的分整参数估计值分别为0.073和0.035，说明两指数的收益率存在较弱的长记忆性，与前面的长记忆检验结果一致。

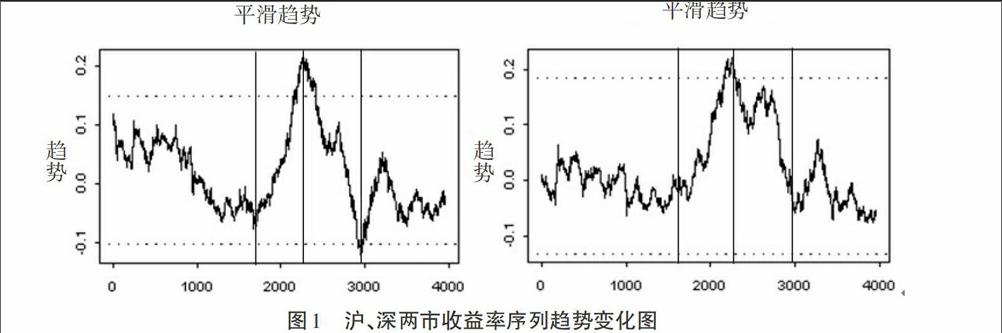
由图1的沪、深两市收益率序列的趋势变化图可以看出，上证综指和深圳成指的趋势变化曲线走势大体相似，大致可分为以下四个变化阶段：（1）1997年至2004年间曲线均落在置信区间内，中间有几次较大的波动，但总体呈现出下降的变化趋势，且上证综指的下降趋势较为明显。（2）2004年至2007年间沪、深两市的趋势函数快速上涨，且穿过置信区间上限，均达到最大值，表明此阶段确定性趋势显著存在。在此期间中国股市正经历一次大的牛市，股指在短短两年时间暴涨5倍之多。（3）2007年至2008年10月两市的趋势函数加速下降，其中沪指还一度接近置信区间的下限。（4）2008年11月至2014年期间沪、深两市的趋势函数趋于平稳，在置信区间内小幅波动。通过分析可知，利用SEMIFAR模型对中国股市收益率的阶段性趋势变化一目了然，沪、深两市的确定性趋势变化明显，且两市的长记忆性大部分可由确定性趋势来解释，而随机性趋势则带有少部分长记忆性，这是以往研究模型不能提供的。随着中国股市的不断完善和健康发展，这种趋势变化逐渐减弱。

接下来对沪、深两市收益率和波动率序列建立SEMIFAR-FIGARCH模型，并在误差分布分别服从正态、GED和t分布情况下，综合考察信息准则Akaike、Schwartz、Hannan-Quinn、Shibata的估计值，得到误差分布服从t分布时，建模效果相对较好，因此后面的研究均在误差分布服从t分布下进行，将参数估计值代入（1）式中，从而得到上证综指和深圳成指的SEMIFAR-FIGARCH估计模型为（4）式和（5）式：

（4）

（5）

从估计模型中可以看出：沪、深两市的收益率存在较弱的长记忆性，深市收益率的长记忆性略高于沪市，而两市波动的长记忆性显著存在，且沪市的波动记忆程度较高。为了对比模型拟合和预测效果，引入ARFIMA-FIGARCH模型、ARFIMA-HYGARCH模型进行比较分析，比较结果见表3：综合四个信息准则估计值结果，沪、深两市的SEMIFAR-FIGARCH模型的拟合效果均要好于ARFIMA-FIGARCH和ARFIMA-HYGARCH模型，表明利用SEMIFAR-FIGARCH模型对我国股市进行分析研究是适合的。

（四）模型预测结果比较

为了判断SEMIFAR-FIGARCH模型与ARFIMA-FIGARCH、ARFIMA-HYGARCH模型对我国股市波动性的度量效果，对预留样本数据进行预测，将沪、深两市的收益率平方作为各自的实际波动率 ，而由模型（4）和（5）计算得出的方差 作为波动率的预测，评判标准依据下面五种预测误差度量指标：平均平方误差（MSE）、平均绝对误差（MAE）、均方根误差（RMSE）、Theil不等系数（TIC）、对数损失函数（LL），则沪、深两市波动率的各模型预测结果见表4。

由表4的结果可以看出，在五个预测误差度量指标中，沪、深两市SEMIFAR-FIGARCH模型的四个指标值均小于其他两个模型，综合考察五个度量指标，SEMIFAR-FIGARCH模型对我国股市波动率的预测效果要优于ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型。

三、结论与展望

本文在对金融时间序列长期记忆性的模型检验进行整理的基础上，将SEMIFAR模型扩展成SEMIFAR-FIGARCH模型，用于检验我国股市收益率和波动率的长记忆性，同时分析收益率的趋势变化走势，为中国股市长记忆性的研究又提供了一个有力工具。通过以上实证研究，可以得出以下结论：

（1）本文通过SEMIFAR-FIGARCH模型对我国股市的研究表明：沪、深两市的收益率长记忆性较弱，而波动率具有较强的长记忆性，表明我国股市存在潜在的风险。随着国家经济结构的转型，证监会一系列政策的出台，将会有效地缩短股市的记忆长度，以削弱金融市场的风险。

（2）中国股市收益率趋势变化显著，呈阶段式下降或上升，在整个样本区间中上证综指和深圳成指的趋势变化走势相似；与深圳成指相比，上证综指的趋势变化尤为明显，震荡幅度更大，并且两市的趋势变化大部分可由确定性趋势来解释，少量由随机性趋势来承担，这可能与两指数的编制以及人们对经济的预期有关，随着中国股市的不断完善和健康发展，这种趋势变化的震荡幅度会逐渐减小。

（3）通过比较实证结果发现，SEMIFAR-FIGARCH模型不仅能较好地捕捉到金融时间序列趋势的变化，还能有效地提高模型的预测能力，表明利用该模型对我国股市进行研究是适合的。

当然对SEMIFAR-FIGARCH模型仍需更进一步的研究：Feng和Beran将MA过程引入SEMIFAR模型中，得到了SEMIFARMA模型，显然SEMIFARMA模型更一般化，还体现了随机误差的累计影响，后续可以在均值方程SEMIFARMA方面进行深入研究。

参 考 文 献

[1] Greene， M.， Fielitz， B.， “Long-term Dependence in Common Stock Returns”， in Journal of Financial Economics， Vol.4， No.3， 1977.

[2] Barkoulas， J.T.， Baum， C.F.， Travos， N.， “Long Memory in the Greek Stock Market”， in Applied Financial Economics， Vol.10， No.2， 2000.

[3] Sibbertson， P.， “Long Memory in Volatilities of German Stock Returns”， in Empirical Economics， Vol.29， No.3， 2004.

[4] 王春峰、张庆翠、李刚：《中国股票市场收益的长期记忆性研究》，载《系统工程》2003年第1期.

[5] 张维、黄兴：《沪深股市的R/S实证分析》，载《系统工程》2001年第1期.

[6] Granger， C.， Joyeux， R.， “An Introduction to Long Memory Time Series Models and Fractional Differencing”， in Journal of Time Series Analysis， Vol.1， No.1， 1980.

[7] Hosking， J.， “Fractional differencing”， in Biometrika， Vol.68， No.1， 1981.

[8] Kang， S.H.， Yoon， S-M.， “Asymmetric Long Memory Feature in the Volatility of Asian Stock Markets”，. in Asia-Pacific Journal of Financial Studies， Vol.35， No.5， 2006.

[9] 张卫国、胡彦梅、陈建忠：《中国股市收益及波动的ARFIMA-FIGARCH模型研究》，载《南方经济》2006年第3期.

[10] 曹广喜：《我国股市收益的双长记性检验——基于VaR估计的ARFIMA-HYGARCH-skt模型》，载《数理统计与管理》2009年第1期.

[11] 石泽龙、程岩：《基于ARFIMA-HYGARCH-M-VaR模型的亚洲汇率市场均值和波动过程的双长期记忆性测度研究》，载《经济数学》2013年第1期.

[12] Beran， J. ，Ocker， D.， “SEMIFAR Forecasts， with Applications to Foreign Exchange Rates”， in Journal of Statistical Planning and Inference， Vol.80， No.1， 1999.

[13] Beran， J.， Feng， Y.， “Iterative plug-in Algorithms for SEMIFAR Models- definition， Convergence and Asymptotic Properties”， in Journal of Computational and Graphical Statistics， Vol. 11， No.3， 2002.

[14] Feng， Y.， Beran， J.， Keming， Y.， “Modelling Financial Time Series with SEMIFAR-GARCH Model”， in Journal of Management Mathematics， Vol.18， No.4， 2007.

[15] Chikhi， M.， Peguin-Feissolle， A.， Terraza， M.， “SEMIFARMA-HYGARCH Modeling of Dow Jones Return Persistence”， in Computational Economics， Vol.41， No.2， 2013.

[16] 陈秋雨：《中国黄金期货市场特征及风险控制》，浙江大学博士学位论文，2011.

[17] 郑雪峰、陈铭新：《基于SEMIFAR模型的我国股市波动率的长记忆性研究》，载《南京财经大学学报》2012年第2期.

[责任编辑 国胜铁]