一种快速检测房颤方法的研究

一种快速检测房颤方法的研究

梁康，孙迎，陆宏伟，孙方东

上海理工大学 医疗器械与食品学院(上海，200093)

【摘要】该文介绍了一种通过心电图RR间期数据进行快速检测房颤症状的方法。借助MIT-BIH提供的正常窦性心律与房颤数据库，分别提取100个连续RR间期数据，对其进行相空间重构，并构造概率密度函数曲线，通过概率密度函数曲线的偏态系数及曲线峰值对应横坐标位置进行区分房颤与正常窦性心律。结果表明，该方法通过使用100个连续RR间期数据进行区分房颤与正常窦性心律，准确率为0.94，适合快速检测房颤时使用。

【关键词】RR间期；相空间分布；房颤；偏态分析

doi:10.3969/j.issn.1674-1242.2015.02.003

作者简介：梁康,Email:liangkang90@126.com

【中图分类号】R318.04

【文献标志码】A

文章编号：1674-1242(2015)02-0073-05

Abstract【】This paper introduces a method to detect atrial fibrillation rapidly by the RR interval of ECG data. 100 consecutive RR interval data were extracted from the MIT-BIH Normal Sinus Rhythm database and Atrial Fibrillation database. We then reconstructed the phase space and probability density function curve of these data. Distinguishing the normal Sinus Rhythm(NSR) and atrial fibrillation(AF) was performed through comparing the skewness and peak value of the probability density function curves. Result shows that the accuracy is 0.94 when 100 RR interval data is used to detect AF. This method may be applied to detect AF rapidly.

收稿日期：(2015-04-02)

A Rapid Detection Method of Atrial Fibrillation

LIANG Kang, SUN Ying, LU Hongwei, SUN Fangdong

School of Medical Instrument and Food Engineering,

University of Shanghai for Science and Technology (Shanghai, 200093)

【Key words】RR interval, phase space distribution, atrial fibrillation, skewness analysis

0　引言

心房颤动(简称房颤)是一种比较常见的心率失常疾病。房颤发病率伴随年龄的增长而增加，60岁以上人群发病率为5%，80岁以上人群发病率为10%[1]。年龄每增加10岁，房颤发病率就会增加1.4倍[2]。当房颤发作时，人体心率呈现快而不齐的症状，不仅心跳比正常状态下加快，而且非常不整齐，心房失去有效的伸缩功能，心输出量降低，容易导致血栓形成，并引起缺血性中风，危及生命安全[3]。

由于房颤发作时间可能较短，现阶段检测房颤主要通过医院的专业设备动态心电图机进行连续观测[4]，可以起到不错的预防和诊断的效果，但仍然需要可以用于快速检测房颤的方法，且提高房颤的识别率。

目前，基于心电图RR间期的一些心血管疾病研究已有很多，但仅依靠RR间期来检测房颤难度仍然较大。因此，实现通过RR间期来提取特征量，用于快速房颤检测，可在一定程度上降低房颤检测的难度。为此，本文将从心电图RR间期的特征进行分析，以MIT-BIH Atrial Fibrillation Database(房颤数据库)和Normal Sinus Rhythm Database(正常窦性心律数据库)为数据来源，通过相空间理论对正常窦性心律(NSR)与房颤(AF)的RR间期进行理论研究，根据对概率密度函数图像的分析，得出区分NSR与AF的特征量，并验证该方法鉴别NSR与AF的准确性。

1　RR间期特点

目前研究RR间期特点常用的一种方法是借助RR-Lorenz散点图[5]。RR-Lorenz散点图是以混沌理论为依据，根据心电图RR间期的动态变化规律，将心电图RR间期数据通过散点图的形式表现出来，对于样本较大的数据，比传统的AECG分析技术效果好[6]。RR-Lorenz图的作图方式为：以相邻RR间期作为横纵坐标，在平面直角坐标系中进行绘制心电图RR间期的散点集[7]。

本文以MIT心电数据库为例，分别选取3 000个心电数值对比NSR的Lorenz散点图和AF的Lorenz散点图，如图1、2所示。

图1NSR的RR-Lorenz图

Fig.1NSR's RR-Lorenz

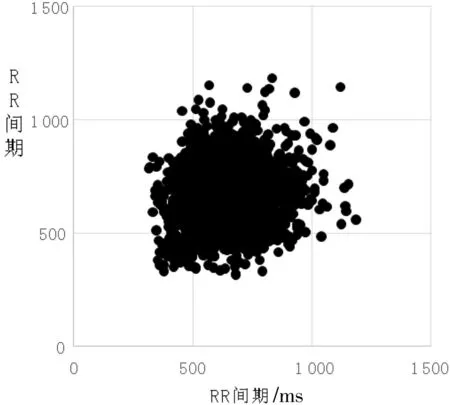
图2AF的RR-Lorenz图

Fig.2AF's RR-Lorenz

从图1、图2可以看出，NSR与AF的RR-Lorenz图差异明显。NSR的RR-Lorenz散点图呈现棒球拍形状，沿着Y=X直线分布比较对称；而AF的RR-Lorenz散点图呈现扇形分布。同时，通过大量的RR-Lorenz散点图观测发现，正常窦性心律心电图的Lorenz图多呈现45°线周围紧密直线排列，而房颤心电图的Lorenz图大多呈现靠近原点的扇形。

因此，NSR与AF的心电图RR间期中存在着不同规律。正常窦性心律心电图的相邻RR间期时间差较小，即相邻两次心搏时间差较小，使得RR-Lorenz散点图呈现直线型排列，而房颤心电图的相邻RR间期差异性比较大，即房颤的相邻心搏时间差异较大，心房激动达到了300～600 次/min，由于存在房室结不应期，快速的心房激动无法全部通过房室结，能最快通过地恰好是Lorenz图中扇形的直线界线[8]。本文同样以混沌理论为基础，借助相空间重构，对NSR与AF进行区分。

2　相空间重构

2.1相空间

相空间重构出现于统计学，由Takens等引入到动力学体系[9]，通过相空间重构的方法，可以将混沌特性的序列重构为非线性动力学系统。将心电图的RR间期作为一个可观测量，根据Takens的嵌入理论，利用RR间期进行相空间重构，同时能够保持系统动力学不变[10]。

对于心电图的RR间期x(n)，n=1,2,3…N，可以构造m维向量y(n)，

y(n)=(x(n)，x(n+t)，…x(n+(m-1)t)

(1)

其中m为嵌入维度，t为延时时间，通过x(n)构造y(n)称为相空间重构。

2.2概率密度函数

在相空间重构的基础上，构造关联的概率密度函数f(m，t，r)计算相空间中的任意两点之间的距离小于r的概率。f(m，t，r)如下所示。

(2)

||·||表示欧几里得距离，h为阶跃函数。

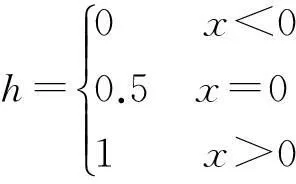
(3)

因此，概率密度函数可以表达为如下公式：

(4)

2.3高斯拟合

为了更准确地进行提取区分NSR与AF的特征参数，本文中对概率密度函数p进行了7点一次线性滤波，并对滤波后的概率密度函数图像进行高斯拟合，通过拟合结果的偏态值与图像峰值进行区分NSR与AF。

3　结果分析

3.1数据选取

本文选择MIT-BIH Atrial Fibrillation Database(房颤数据库)和Normal Sinus Rhythm Database(正常窦性心律)两个数据库中的数据进行算法分析，其中房颤数据库选取207段数据，正常窦性心律数据库中选取208段数据，每段数据内容为100个心电图的连续RR间期，以此用于绘制概率密度函数图像进行区分NSR与AF。使用Java语言编写程序实现绘制概率密度函数图像。

3.2概率密度函数分布图

借助相空间理论及概率密度函数图像，对选取的100个心电图RR间期进行相空间重构，在m维空间中重新构建延时为t的数据，并且以各个数据的距离值构造概率密度函数。由于选取100点心电图的RR间期，数量有限，当维度m与延时t的数值不断增加时，重构后的点数量则不断减少。因此，在满足重构条件的基础上，本文选择维度m=5的图像进行处理，如图3所示。

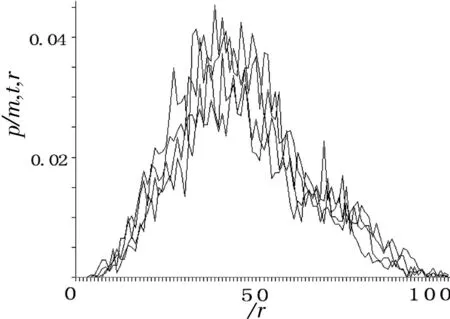
图35维原始概率密度函数图像

Fig.3Original probably density function curve atm=5

3.3滤波拟合

获得维度m=5条件下多个延时t的概率密度函数图像后，仍需对其进行滤波处理，使图像平滑显示，便于图像进行拟合，从而提取特征量。在保证图像信息的最小损失前提下，使图像更顺滑，本文选择使用7点一次滤波方法进行处理，图3中的图像经7点一次滤波后的结果见图4所示。

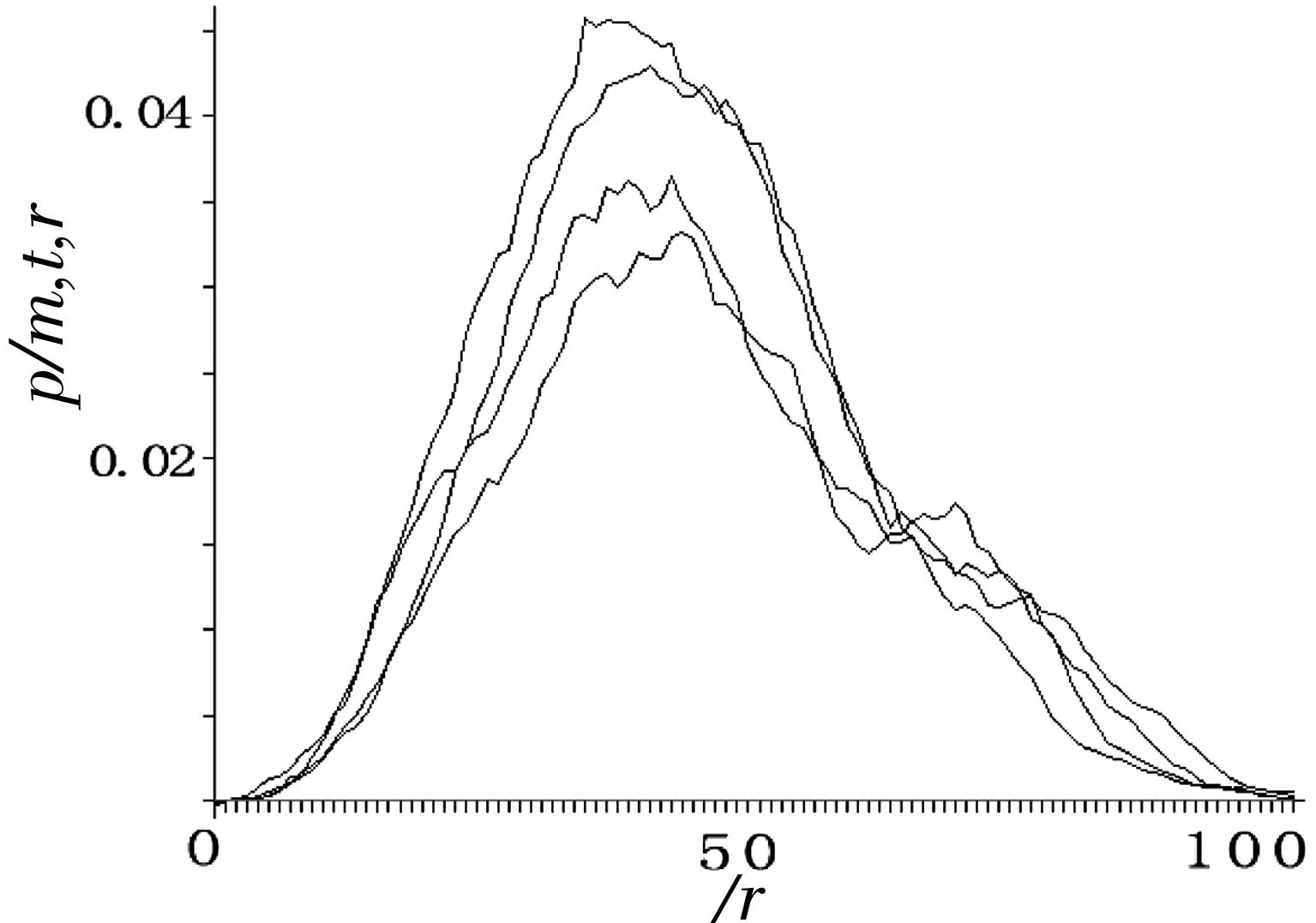
图4滤波后概率密度函数图像

Fig.4probably density function after filtering

通过对208段正常窦性心律心电数据与207段房颤数据分别采样100个RR间期进行重构相空间并绘制概率密度函数图像，发现正常窦性心律的概率密度函数图像接近于对数正态分布(如图5)，而房颤数据的概率密度函数图像接近于正态分布(如图6)。

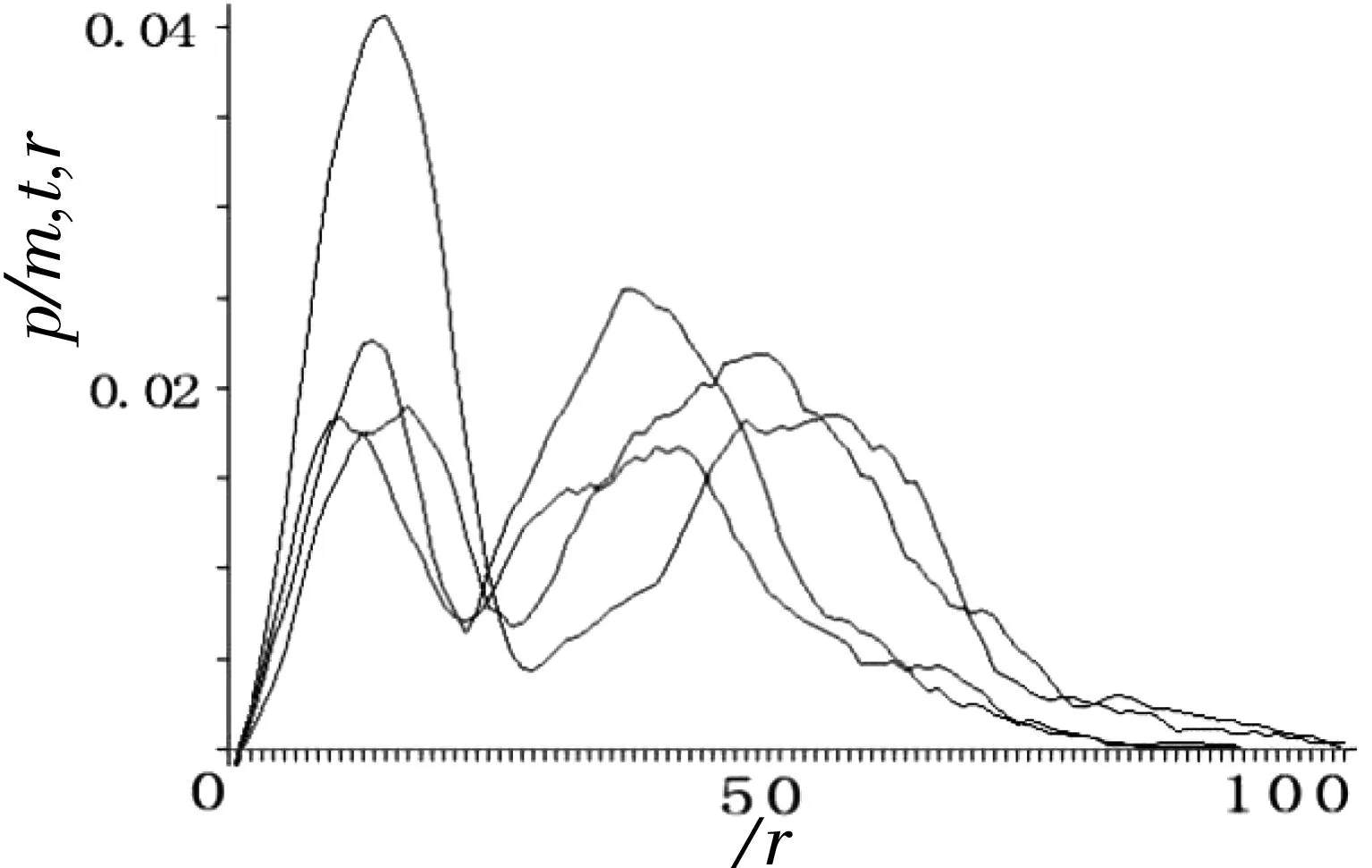
图5NSR的概率密度函数图像

Fig.5Probably density function curve of NSR

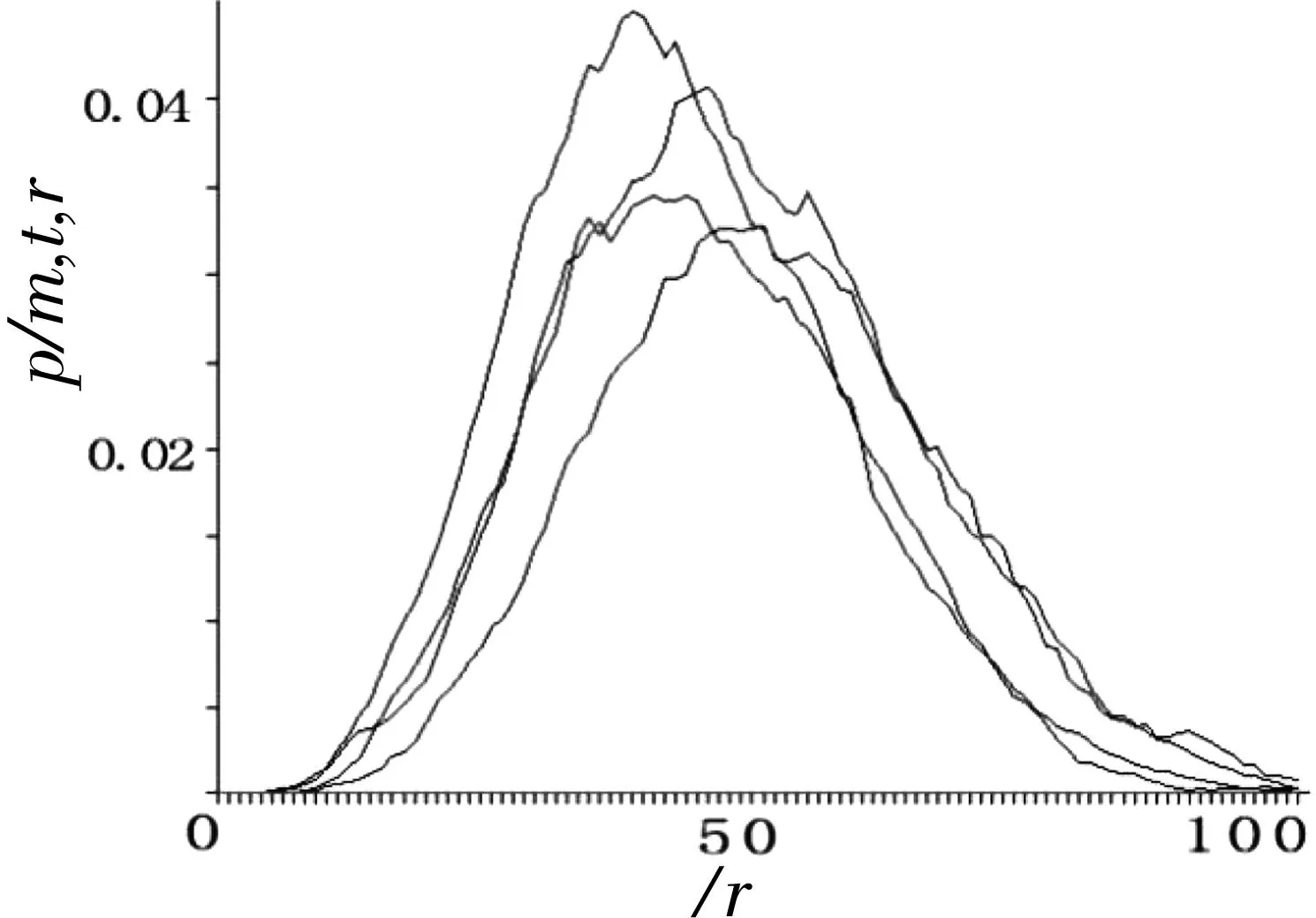
图6　AF的概率密度函数图像

滤波后的概率密度函数图像中，维度m=5时，延时t值越大，图像的特征越不明显，因此选用延时t=1的曲线进行拟合，并提取特征参数。

借助计算机辅助技术，使用Origin软件对滤波后的概率密度函数图像中维度m=5，延时t=1进行高斯函数图像拟合，如图7、图8所示，分别为正常窦性心律与房颤的RR间期概率密度函数图像的拟合曲线，拟合R平方值均在0.95以上。

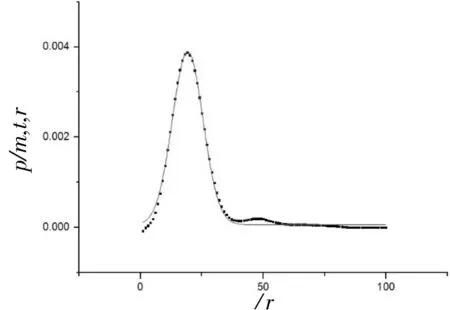
图7NSR的拟合曲线

Fig.7Fitting curve of NSR

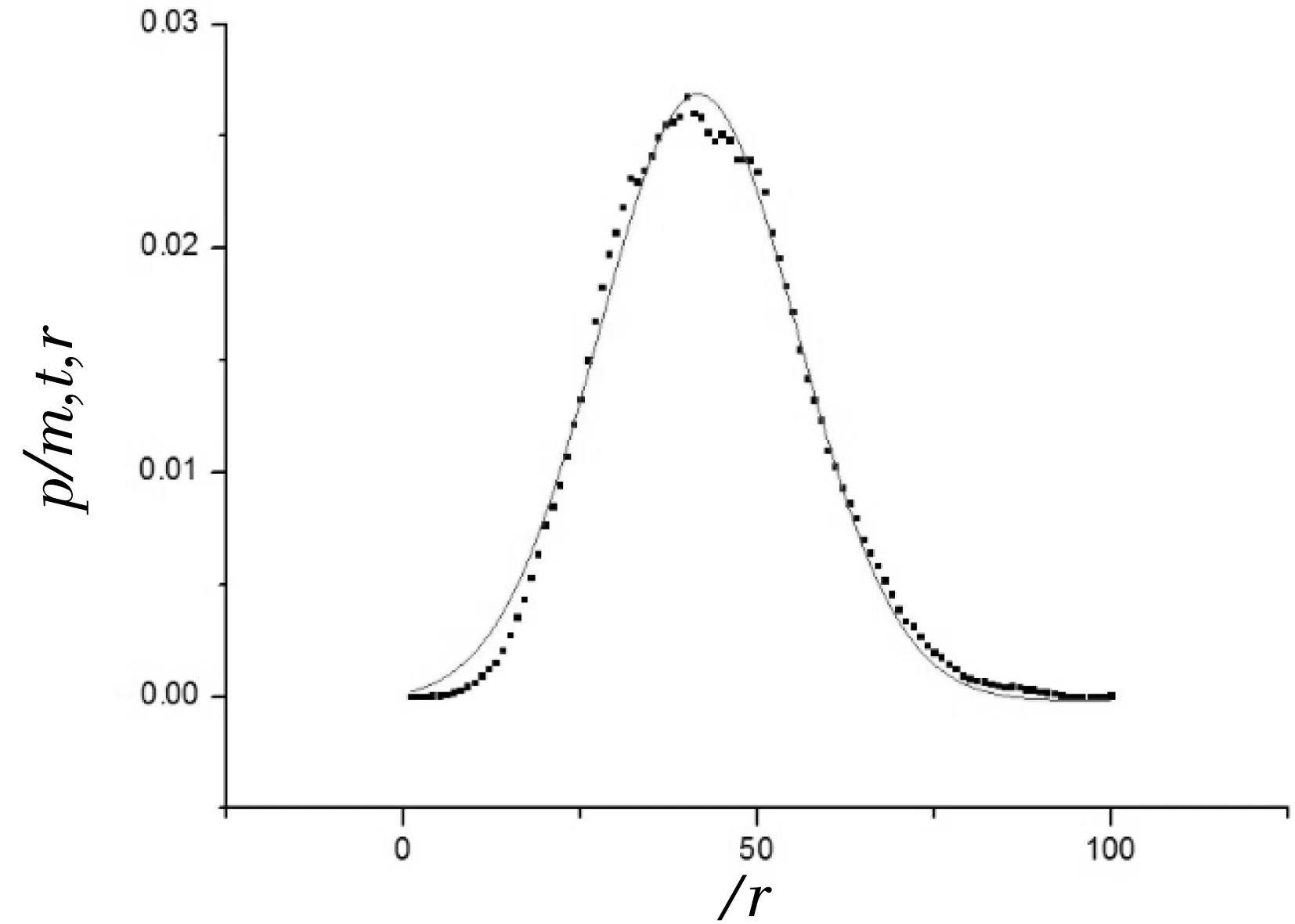
图8　AF的拟合曲线

3.4偏态分析

由于检测结果符合正态分布或对数正态分布，因此可通过正态分布的特征值进行区分正常窦性心律与房颤的概率密度图像。本文中使用概率密度曲线的偏态系数与曲线峰值横坐标位置两个特征来区分NSR与AF。

其中，偏态系数Skew方法为：

(5)

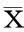
通过对MIT-BIH的208段正常窦性心律心电数据与207段房颤心电数据进行偏态系数计算，部分数据如表1所示。

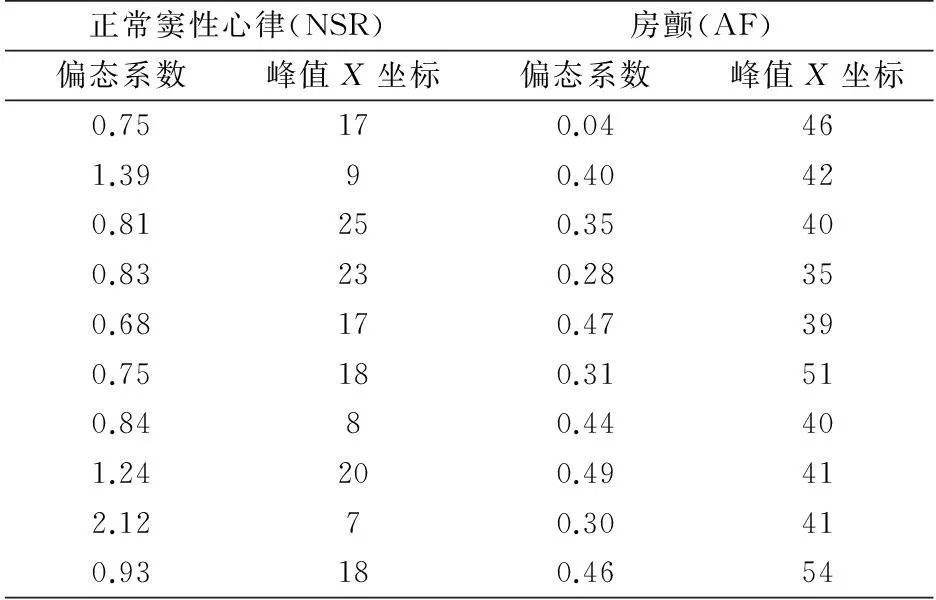
表1　NSR与AF数据偏态系数对比

统计结果发现，房颤的概率密度函数图像的偏态系数小于1且曲线峰值对应横坐标X(0≤X≤100)均大于33，正常窦性心律的概率密度函数图像的偏态系数则变化较大，且比多数房颤的偏态系数大，峰值横坐标X则小于33。

结果中房颤概率密度曲线呈现出的明显特点，是由于房颤与正常窦性心律相比，房颤的RR间期关联性比正常窦性心律弱[11]，房颤RR间期具有更明显的不规则性，随机性较强，房颤的概率密度曲线更加接近正态分布，峰值位于整体曲线的中心部分；而正常窦性心律的概率密度曲线则是更加接近对数正态分布，峰值位于整体曲线左部分。

因此，以此偏态值与横坐标作为阈值，进行区分房颤与正常窦性心律，得出结果为表2所示。

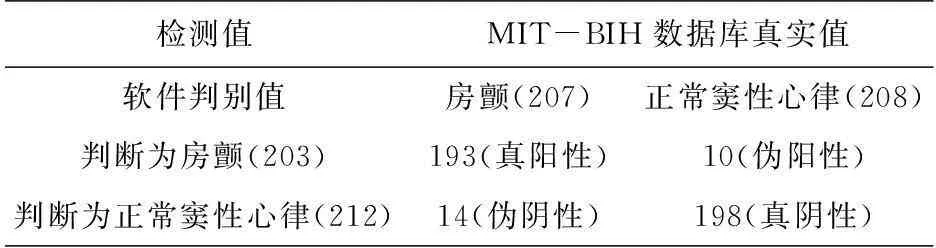
表2　准确率检验

统计结果发现，208段正常窦性心律心电数据与207段房颤心电数据使用偏态系数及曲线峰值横坐标位置作为阈值进行区分，房颤心电数据概率密度曲线图的偏态系数均小于1且曲线峰值横坐标X>33，且房颤的概率密度曲线呈正态分布曲线；

正常窦性心律数据概率密度曲线图的偏态系数则不规则，而曲线峰值横坐标X<33。通过该方法进行区分房颤与正常窦性心律的灵敏度为0.93，特异度0.95，准确率为0.94。

4　结论

本文借助了MIT-BIH提供的正常窦性心律数据库与房颤数据库的心电数据，从每段数据中提取连续100个心电图的RR间期数据，并使用相空间方法进行重构，在维度m=5，t=1的情况下绘制概率密度函数的曲线图，对曲线进行线性滤波和高斯拟合，最终发现房颤数据与正常窦性心律数据的概率密度曲线有明显区别，并以曲线的偏态系数及峰值横坐标位置进行判断，准确率为0.94。

本文中判断房颤与正常窦性心律的方法已在JAVA平台上实现，以后将可在移动平台(Android/iOS)上进行实现，更加方便用户进行检测。同时，作者将继续对房颤与正常窦性心律心电数据进行研究，进一步提高房颤检测的准确度。

致谢：感谢MIT-BIH数据库提供的心电数据。

参考文献

[1] Pagana G, Galleani L, Gross S, et al. Time-frequency analysis of the endocavitarian signal in paroxysmal atrial fibrillation[J]. IEEE T Bio Med Eng, 2012, 59(10):2838-2844.

[2] CD F, BM P, TA M, et al. Prevalence of atrial fibrillation in elderly subjects (the cardiovascular health study)[J]. Am Cardiol, 1994, 74(3):236-241.

[3] Brunner KJ, Bunch TJ, Mullin CM, et al. Clinical predictors of risk for atrial fibrillation: implications for diagnosis and monitoring[J]. Mayo Clin Proc, 2014, 89(11):1498-1505.

[4] Pürerfellner H, Pokushalov E, Sarkar S, et al. P-wave evidence as a method for improving algorithm to detect atrial fibrillation in insertable cardiac monitors[J]. Heart Rhythm, 2014, 11:1575-1583.

[5] 刘雁, 慕德俊, 焦永锋,等. R-R Lorenz图实现心电信号混沌特征识别的研究[J]. 北京生物医学工程, 2008, 27(1):37-40.

[6] 李方洁, 曾辉, 郭小玉. 宽 QRS 波 Lorenz 散点图的鉴别诊断[J]. 中国循环杂志, 2006, 21(8): 230-232.

[7] 王步青, 王卫东. 心率变异性分析方法的研究进展[J]. 北京生物医学工程, 2007, 26(5):551-554.

[8] 李方洁, 向晋涛. 心电散点图呈现的房室结功能不应期及对宽QRS波的鉴别[J]. 中国心脏起搏与心电生理杂志, 2011, 25(1):16-19.

[9] Roterman Y, Porat M. Color image coding using regional correlation of primary colors[J]. Image Vision Comput, 2007, 25(5):637-651.

[10] Li J, Dunmire B, Beach KW, et al. A reflectance model for non-contact mapping of venous oxygen saturation using a CCD camera[J]. Opt Commun, 2013, 308(11):78-84.

[11] 陆宏伟, 林敏, 孙迎,等. 房颤R-R间期关联性比正常窦性心律弱[J]. 上海理工大学学报, 2007, 29(5):445-448.