三个五阶非线性方程的精确解

钟鸣华，　那仁满都拉，　斯仁道尔吉

(内蒙古师范大学数学科学学院,呼和浩特010022)

三个五阶非线性方程的精确解

钟鸣华，那仁满都拉，斯仁道尔吉

(内蒙古师范大学数学科学学院,呼和浩特010022)

[摘要]为了得到三个五阶非线性方程的精确解，本文通过假设行波解将三个五阶非线性方程化为常微分方程并借助辅助方程法和Mathematica软件对其求解,最终获得了一系列精确解.

[关键词]五阶非线性方程; 辅助方程法; 精确解

1引言

非线性偏微分方程在现实生活以及生物、物理等邻域中有着重要而广泛的应用,因此非线性偏微分方程的求解问题就成为非线性科学的前沿研究课题之一.到目前为止，数学和物理工作者在求解非线性偏微分方程的领域积累了大量的经验并先后提出了一系列求解方法,这些方法在许多具体的方程上都得到了应用,如Jacobi椭圆函数法[1]、齐次平衡法[2]、完全近似法[3]、试探函数法[4]、双曲函数展开法[5]、约化摄动法[6]、F-展开法[7]、Exp函数法[8]、辅助方程法[9]等都在具体的文献中被引用,并作为主要求解方法.本文运用辅助方程法精确求解文献[10]中提出的如下三个方程

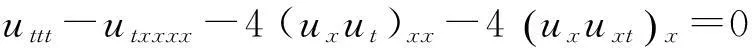
(1)

(2)

(3)

并且得到一些新的精确解.

2方法介绍

考虑如下形式的非线性偏微分方程

N(t,x,u,ut,ux,uxx,…)=0,

(4)

假设其行波解为

u(x,t)=u(ξ),ξ=kx-vt，

(5)

其中k和v是待定常数,则方程(4)可转化为下面形式的常微分方程

F(u,u′,u″,u‴,…)=0,

(6)

其中“′”是函数u关于ξ的导数.

设方程(6)有如下形式的解

(7)

其中φ(ξ)满足辅助方程

φ′(ξ)2=b0+b1φ(ξ)+b2φ(ξ)2+b3φ(ξ)3+b4φ(ξ)4,

(8)

这里n是根据方程中最高阶导数项和最高次幂的非线性项平衡得到的ai,bj,j=0,1,2,3,4是待定常数.

把(7),(8)带入到(6),令φ(ξ)的各次幂的系数为零而得到一个非线性代数方程组并求解可得到待定的系数ai,bj.

由文献[11]和[12]知,辅助方程(8)有如下几种解:

解(一)当b0=b1=b3时,(8)具有钟状孤子解、三角函数解和有理解:

(9)

(10)

(11)

(12)

(13)

(14)

解(三)当b0=b1=0,(8)具有如下几种解:

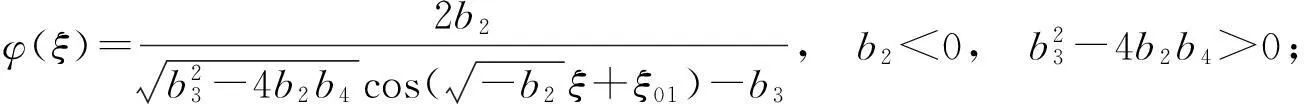
(15)

(16)

(17)

(18)

解(四)当b0=b1=b4=0时,(8)具有如下钟状孤子解、三角函数周期解和有理解:

(19)

(20)

(21)

解(五)当b4=0,b3>0时,(8)具有Weierstrass椭圆函数解:

(22)

3方程(1)的精确解

假设方程(1)的行波解为

代入方程,积分两次并取积分常数均为零,则有如下常微分方程

v2u′(ξ)-k4u‴(ξ)-6k3u′(ξ)2=0.

(23)

设u′(ξ)=w(ξ),则以上方程变为

v2w(ξ)-k4w″(ξ)-6k3w(ξ)2=0.

(24)

根据平衡最高阶导数项和最高幂次的非线性项,得到n=2,所以,设方程(24)有如下形式的解

w(ξ)=a0+a1φ(ξ)+a2φ(ξ)2，

(25)

其中φ(ξ)满足方程(8).把(8)和(25)代入到(24),化简后,令φ(ξ)n的系数为零,得到如下关于a2,a0,a1,b2,b0,b1,b3,b4,k,v的超定代数方程组

利用Mathematica软件,解方程组,得如下两组解:

把(Ⅰ)代入到解(四)有

①b2>0时,

则代入到(25)可得w(ξ),对w(ξ)求不定积分,即得

②b2<0时,

则代入到(25)可得w(ξ),对w(ξ)求不定积分,即得

把(Ⅰ)代入到解(五)有:b4=0且b3>0时,

则代入到(25)可得w(ξ),对w(ξ)求不定积分即可得原方程的解u(ξ).

把(Ⅱ)代入到解(一)有

①b2>0,b4<0时,

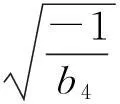
②b2<0,b4>0时,

③b2=0,b4>0时,

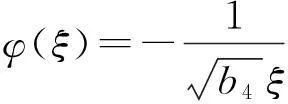
代入到(25)可得w(ξ),对w(ξ)求不定积分,即得

把(Ⅱ)代入到解(二)有

①b2<0, b4>0时,

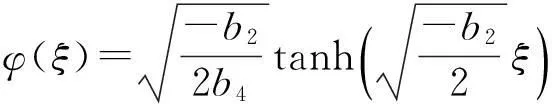
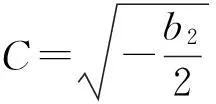
u(ξ)=(a0-kC2)ξ+Cktanh(Cξ)+c21.

②b2>0, b4>0时,

u(ξ)=(a0+kD2)ξ-Dktan(Dξ)+c22.

情形1:b3=0,则代入(Ⅱ)可得

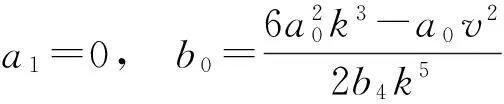
由b0=0可得

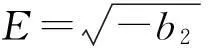
代入(Ⅱ)有

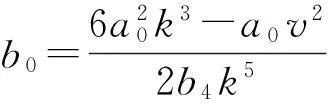
由于(Ⅱ)中b4≠0,所以不把(Ⅱ)代入到解(四)和解(五)研究.

4方程(2)的精确解

同第一个方程的精确解的求法一样, (2)经行波变换后化为

(v2-k2)w(ξ)-k4w″(ξ)-6k3w(ξ)2=0.

(26)

利用Mathematica软件,解平衡后得到的方程组,得如下两组解:

把(Ⅰ)代入到解(四)有:由b1=0可得

①b2>0时,

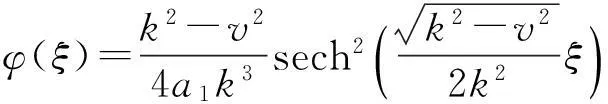
则有

②b2<0时,

则有

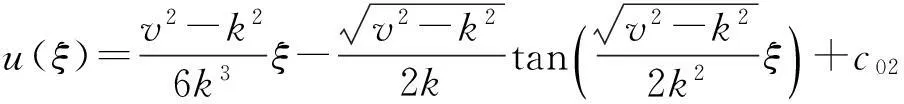
③b2=0时,可得

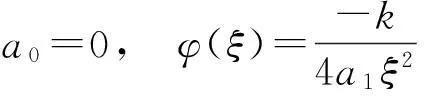
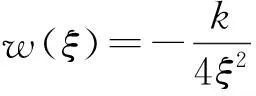
把(Ⅰ)代入到解(五)有:b4=0且b3<0时,则有

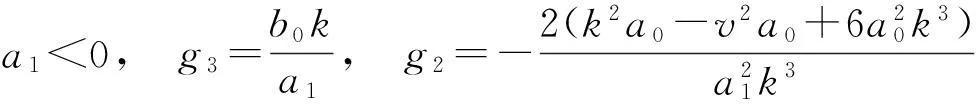
则

对w(ξ)求不定积分即可得原方程的解u(ξ).

把(Ⅱ)代入到解(一)有

①b2>0, b4<0时,

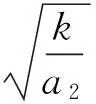
②b2<0, b4>0时,

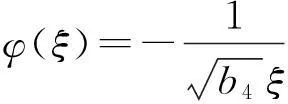
①b2<0, b4>0时,

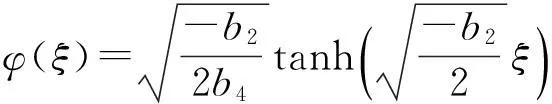
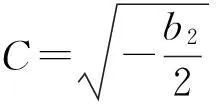
u(ξ)=(a0-kC2)ξ+kCtanh(Cξ)+c21.

②b2>0,b4>0时,

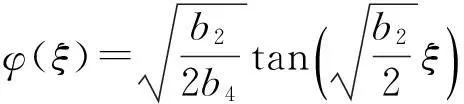
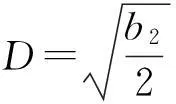
u(ξ)=(a0+kD2)ξ-Dktan(Dξ)+c22.

把(Ⅱ)代入到解(三)有:由b1=0可得

情形1:a1=0,则代入(Ⅱ)且由b0=0得

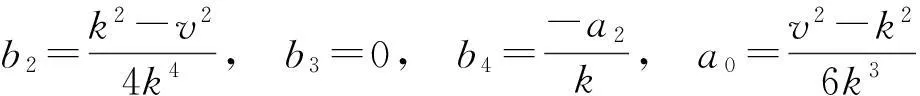
① 当b2<0,b4>0时,则

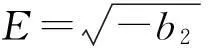
② 当b2>0,b4<0时,则

③ 当b2>0,b4>0时,则

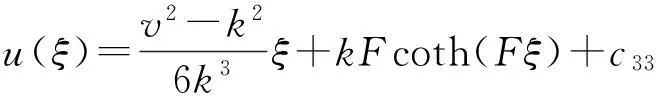
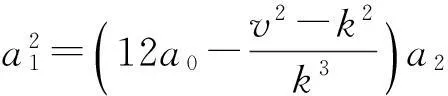
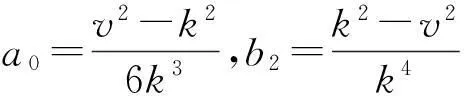
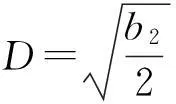
由于(Ⅱ)中b4≠0,所以不把(Ⅱ)代入到解(四)和解(五)研究.

5方程(3)的精确解

方法同上,解不定方程组可得下面两组解:

把(Ⅰ)和(Ⅱ)分别代入解(一)、解(二)、解(三)、解(四)、解(五),可得如下解:

本文用行波变换后把三个五阶非线性方程转化为常微分方程,再利用辅助方程法得到了这三个方程的一系列精确解,并且这些解都是首次给出的.

[参考文献]

[1]刘官厅,范天佑.一般变换下的Jacobi椭圆函数展开法及应用[J].物理学报, 2004, 53(3): 676-679.

[2]张解放. 变更Boussinesq方程和Kupershmidt方程的多孤子解[J].应用数学和力学, 2000, 21(2): 171-175.

[3]郭鹏,张磊,吕克璞,段文山.一类非线性弹性杆波动方程的求解[J].应用数学和力学,2008,29(1):57-61.

[4]武祥,郭鹏,刘远聪.一类非线性粘性弹性杆波动方程的求解[J].科技信息, 2008(2):203.

[5]杨建荣,毛杰健,张解放.一维弹性杆的非线性波动方程的孤波解[J].毕节师范高等专科学校学报, 2001, 19(4):48-50.

[6]吕克璞,郭鹏,张磊等.非线性弹性杆波动方程的摄动分析[J].应用数学与力学, 2006, 27(9): 1079-1083.

[7]张平.关于一类五阶非线性发展方程的新精确解[J].五邑大学学报(自然科学版), 2008, 22(1): 35-39.

[8]杨昆望.应用指数函数展开法求解非线性发展方程[J].纯粹数学与应用数学,2012,01:85-91.

[9]Sirendaoreji.Auxiliaryequationmethodforsolvingnonlinearpartialdifferentialequations[J].PhysicsLettersA, 309(5-6)(2003):387-396.

[10]Abdul-MajidWazwaz.Kinksolutionsforthreenewfifthordernonlinearequations[J].AppliedMathematicalModelling,2014,33:110-118.

[11]长勒.几类非线性演化方程的精确类孤子解[D].内蒙古：内蒙古师范大学数学科学学院, 2012.

[12]郭玉翠.非线性偏微分方程引论[M].北京:清华大学出版社, 2008.

ExactSolutionsforThreeFifthOrderNonlinearEquations

ZHONG Ming-hua，Narenmandula，Sirendaoerji

(MathematicalScienceCollege,InnerMongoliaNormalUniversity,Huhhot, 010022,China)

Abstract:Inordertoobtainthethreefifth-ordernonlinearequationexactsolution.Inthispaper,byassumingthetravellingwavesolutionsofthreefifth-ordernonlinearequationsintoordinarydifferentialequationandwiththeaidoftheauxiliaryequationmethodandMathematicasoftwaretosolvethem.Finallyweobtainaseriesofexactsolutions.

Keywords:fifth-ordernonlinearequation;auxiliaryequationmethod;exactsolution

[中图分类号]O175.2

[文献标识码]A

[文章编号]1672-1454(2015)04-0070-09