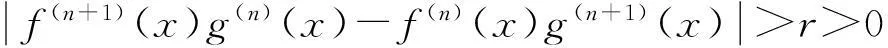几类中值定理中间点的分析性质

傅新梅,　刘　晴,　李宏亮

(1.浙江外国语学院数学系，杭州310012;　2. 杭州市大禹路小学， 杭州310012)

几类中值定理中间点的分析性质

傅新梅1,刘晴2,李宏亮1

(1.浙江外国语学院数学系，杭州310012;2. 杭州市大禹路小学， 杭州310012)

[摘要]给出了广义Taylor公式、高阶Cauchy中值定理及加权型中值定理中间点的单值性、连续性及可导性的充分条件，并给出了求导公式.

[关键词]Taylor公式； 中间点； 单值； 连续； 可导

1引言

2007年刘龙章、戴立辉、杨志辉[1]讨论了Lagrange中值定理和Cauchy中值定理中间点ξ的单调性、连续性及可导性问题.2009年程希旺[2]则对Taylor中值定理中间点ξ的单值性、连续性及可导性问题进行研究分析.2012年时统业、谢井、李鼎[3]引进一个新函数F(h(x),k)，用较简便的方法讨论了Taylor中值定理中间点ξ的单值性、连续性及可导性问题.

本文主要对广义Taylor公式、高阶Cauchy中值定理及加权型中值定理的中间点的单值性、连续性及可导性问题进行研究.

2引理

引理1(广义Taylor公式[4])设函数f(x)和g(x)在[a,b]上具有n-1阶连续导数，在[a,b]内f(n)(x)和g(n)(x)存在，且g(n)(x)≠0则对任何x∈(a,b)至少存在一点ξ∈(a,x),使

(1)

引理2(高阶Cauchy中值定理[4])设函数f(x)和g(x)在[a,b]上具有n-1阶导数，在(a,b)内具有n阶导数，且g(n)(x)≠0则对任何x∈(a,b)至少存在一点ξ∈(a,x)使

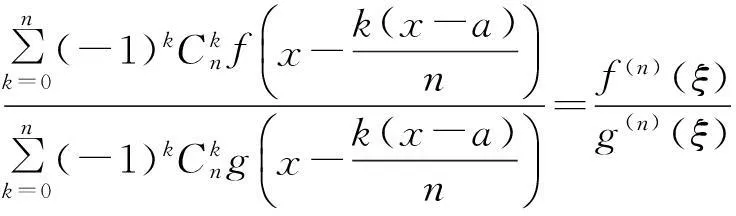
(2)

引理3[5]设函数f(x),g(x)满足

(i) 在区间[a,x]上有定义，且有n-1阶的连续导数f(n-1)(x),g(n-1)(x)，

(ii) 在开区间(a,x)内有n阶导数，且

0

则至少存在点ξ∈(a,x)，使

(3)

其中

3结论

定理1设函数f(x)和g(x)在[a,b]上n+1阶连续可导，且

g(n)(x)≠0，f(n+1)(x)g(n)(x)-f(n)(x)g(n+1)(x)

在(a,b)内保号(恒正或恒负)，则

(i) 满足(1)式的“中间点”ξ=ξ(x)是x的单值连续函数；

(ii) 满足(1)式的“中间点”ξ=ξ(x)是x的可导函数，当n=1时，其导数为

当n≥2时其导数为

由已知条件g(n)(x)≠0，f(n+1)(x)g(n)(x)-f(n)(x)g(n+1)(x)在(a,b)内保号(恒正或恒负)，可知φ(x)是单调函数，那么(1)式的“中间点”ξ=ξ(x)是x的单值函数.另一方面

其中ξ(x)介于a,x之间，ξ(x+Δx)介于a,x+Δx之间，η介于ξ(x),ξ(x+Δx)之间.

令

由于f(n+1)(x)g(n)(x)-f(n)(x)g(n+1)(x)在(a,b)内保号且f(n+1)(x),g(n+1)(x)连续，故存在ξ(x)的一个领域∪(ξ(x),δ)，使得

因此

=0.

故满足(1)式的“中间点”ξ=ξ(x)是x的单值连续函数得证，即结论(i)成立.且

将F′(x)和G′(x)带入上式，就能分别得到当n=1和n≥2时的导数公式，即结论(ii)成立.

注1(i) 当g(x)=(x-a)n时，那么f(n+1)(x)g(n)(x)-f(n)(x)g(n+1)(x)在(a,b)内保号，即f(n+1)(x)保号. 故定理1是[2]中定理2的推广.

(ii) 当n=1时，广义Taylor公式为Cauchy中值定理.故定理1是对[1]中定理3的推广.

对高阶Cauchy中值定理类似于定理1的证明可得到下面的结论.

定理2设函数f(x)和g(x)是[a,b]上n+1阶连续可导，且

g(n)(x)≠0，f(n+1)(x)g(n)(x)-f(n)(x)g(n+1)(x)

内保号(恒正或恒负)，则

(i) 满足 (2)式的“中间点”ξ=ξ(x)是x的单值连续函数；

(ii) 满足 (2) 式“中间点”ξ=ξ(x)是x的可导函数，其导数为

对于加权型中值定理也有下面的结果.

定理3设函数f(x)和g(x)是[a,b]上n+1阶连续可导，且

g(n)(x)≠0，f(n+1)(x)g(n)(x)-f(n)(x)g(n+1)(x)

在(a,b)内保号(恒正或恒负)，则

(i) 满足(3)式的“中间点”ξ=ξ(x)是x的单值连续函数；

(ii) 满足(3)式的“中间点”ξ=ξ(x)是x的可导函数，导数为

其中

其中Tn=1.

证类似于定理1中(i)的证明可得结论(i)成立.利用定理1中(ii)的证明方法结合行列式的求导公式以及行列式的相关性质可得结论(ii)成立.

[参考文献]

[1]刘龙章，戴立辉，杨志辉.再论微分中值定理“中间点”ξ的性质[J].大学数学， 2007，23(4)：164-166.

[2]程希旺. 泰勒中值定理中值点的分析性质[J].数学的实践与认识，2009，39(4)：236-238.

[3]时统业，谢井，李鼎.论泰勒中值定理中间点的性质[J].大学数学，2012，28(4)：121-123.

[4]苗俊岭.广义微分中值定理中间值的渐近性[J].黑龙江农垦师专学报，2001，4(58)：88-90.

[5]马跃超，陈侠.加权型中值定理[J].沈阳航空工业学院学报，2002，19(2)：63-65.

TheIntermediatePoint’sAnalyticalPropertiesofSomeKindsofMeanValueTherom

FU Xin-mei1，LIUQing2，LIHong-liang1

(1.DepartmentofMathematics,ZhejiangInternationalStudiesUniversity,Hangzhou, 310012,China；

2.HangzhouDaYuluPrimarySchool,Hangzhou310030,China)

Abstract:WeobtainsomesufficientconditionsfortheintermediatepointsofgeneralTaylorformula,highorderCauchy’smeanvaluetheoremandtheweightedmeantheoremtohavesingle-value,continuity,differentiability.Atthesametime,wegetformulaetocalculatederivatives.

Keywords:generalTaylorformula;intermediatepoint;single-valued;continuity;derivative

[基金项目]国家自然科学基金(11371048)； 北京建筑大学双语课程建设(常微分方程)；北京建筑大学稳定性理论优质课程(K2015004)

[收稿日期]2015-02-13；[修改日期]2015-05-31

[中图分类号]O156

[文献标识码]C

[文章编号]1672-1454(2015)04-0060-04