Colebrook-White方程三个显式公式的重制
2015-12-21贾美胜杨康魏兰洪艳萍张禹江西省天然气投资有限公司江西南昌330096江西省天然气有限公司江西南昌330096
贾美胜 杨康 魏兰 洪艳萍 张禹(.江西省天然气投资有限公司,江西 南昌 330096;.江西省天然气有限公司,江西 南昌 330096)
1 Colebrook-White方程
在计算摩阻系数的众多方程中,最常用的就是Colebrook-White方程,它是一个经验公式[1,2]

表1 Colebrook-White方程的不同显式形式
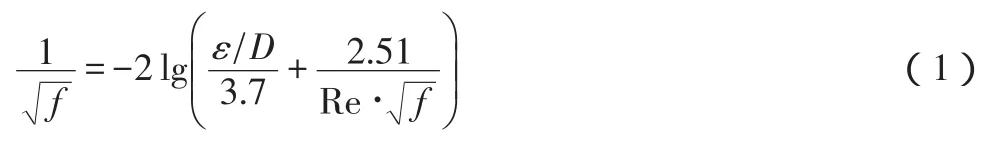
该公式与摩擦系数f有关,同时还与管道粗糙度和雷诺数Re有隐性关联.
2 显式Colebrook-White方程的关联性
解决摩阻系数是一个复杂的过程,由于Colebrook-White方程的隐式形式,设计者在最初用使用该方程时,需要借助图表进行估算.随着计算机的应用,可以运用迭代算法,如弦截法、抛物线法等来求解该方程.但是这样用起来仍然不方便.于是,各种显式Colebrook-White方程便应运而生.表1中的公式是最常见和精确的显式公式.
2.1 显式Colebrook-White方程的代表
表1中公式1和公式6为Zigrang和Sylvester提出的公式(1982);公式2为Barr提出的公式(1981);公式3为Serghides提出的公式(1984);公式4为chen提出的公式(1979);公式5为Romeo提出的公式(2002);公式7为Serghides提出的公式(1984);公式8和9为C.T.GOUDAR和J.R.SONNAD提出的公式(2008);公式8和9为苑伟民提出的公(2013)[11].
2.2 三个高精确度显式Colebrook-White方程的研究
为获得计算摩阻系数的高精度和简单形式的显式方程,数值计算法应用而生.
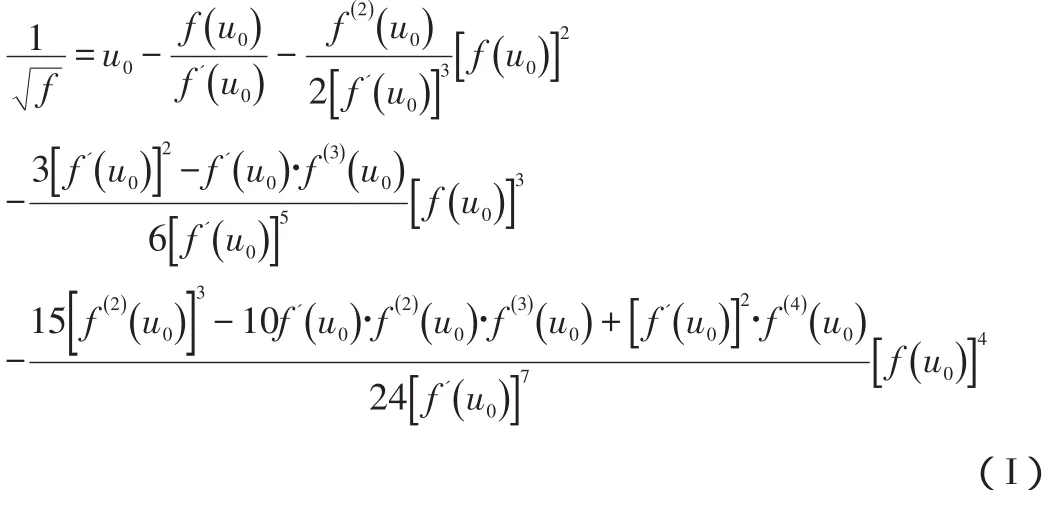
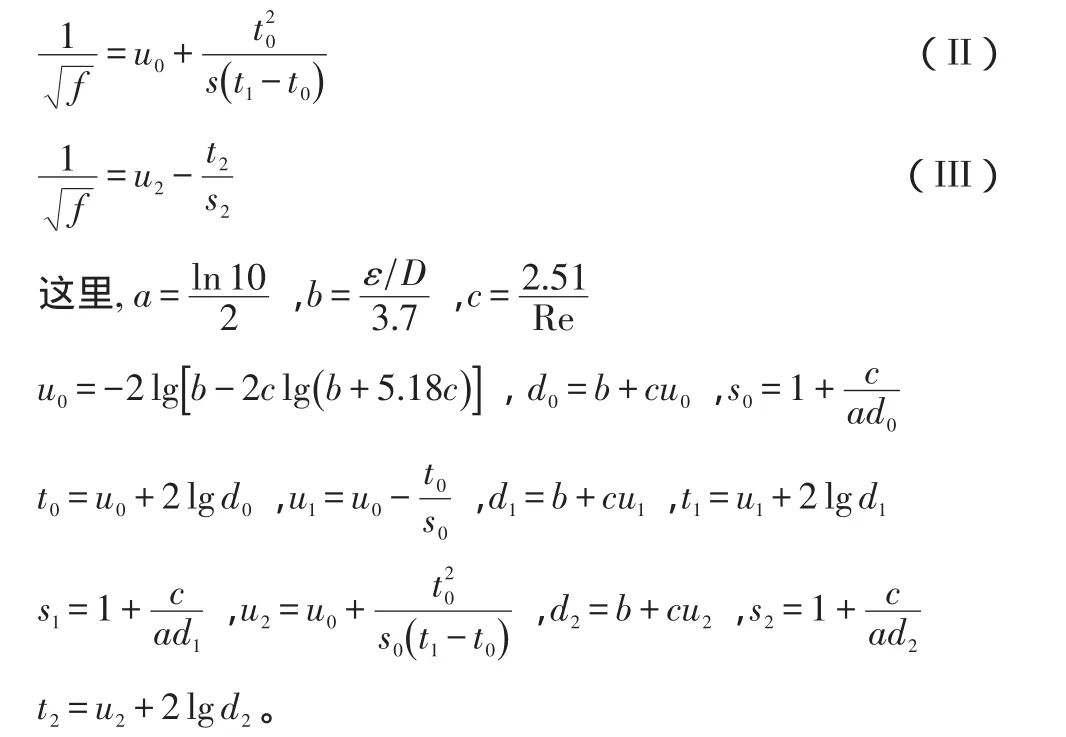
公式1非常复杂,公式2和公式3相对简单,但它们都能得到高精确度数值.
3 显式公式的对比研究
计算了500个f值和它们的相对误差还有绝对误差,表2显示了最大误差值.表2中的值在整个测量范围内(Re∈(0,106)不是都有效的,但是我们可以估算整个紊流区对运行环境的影响.
3.1 数据(如表2、表3)
3.2 对比方法:连续计算50000次摩阻系数f.
表4中,公式a and公式b是弦截法求解方程,公式1到9与表1相关联,公式(I)到(III)是本文介绍的方法.
由于计算机起始工作状态不同,表4中的计算时间仅作为参考.
4 结语
4.1 表1中,方程的精度能够满足工程需要.
4.2 显式公式的计算精度和耗时均优于迭代计算法.
4.3 本文中的新公式与Colebrook-White方程相比可以减少9.992E-12%的相对误差,1.050E-15的绝对误差,其结果优于其它公式.
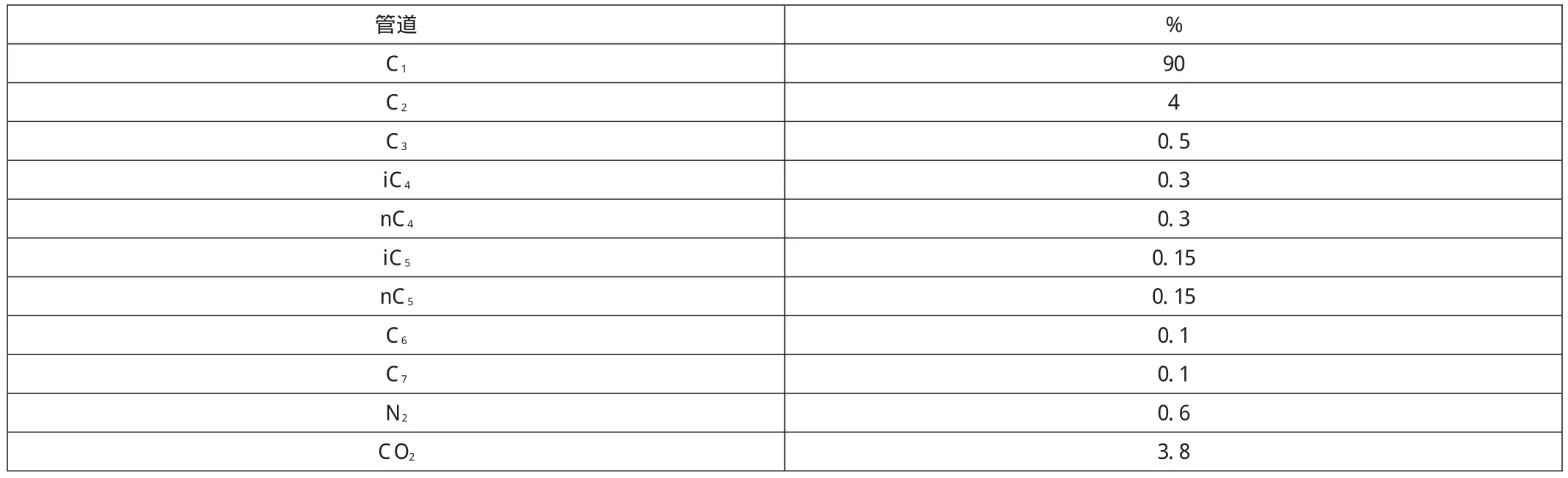
表2 气体组分

表3 记录数据
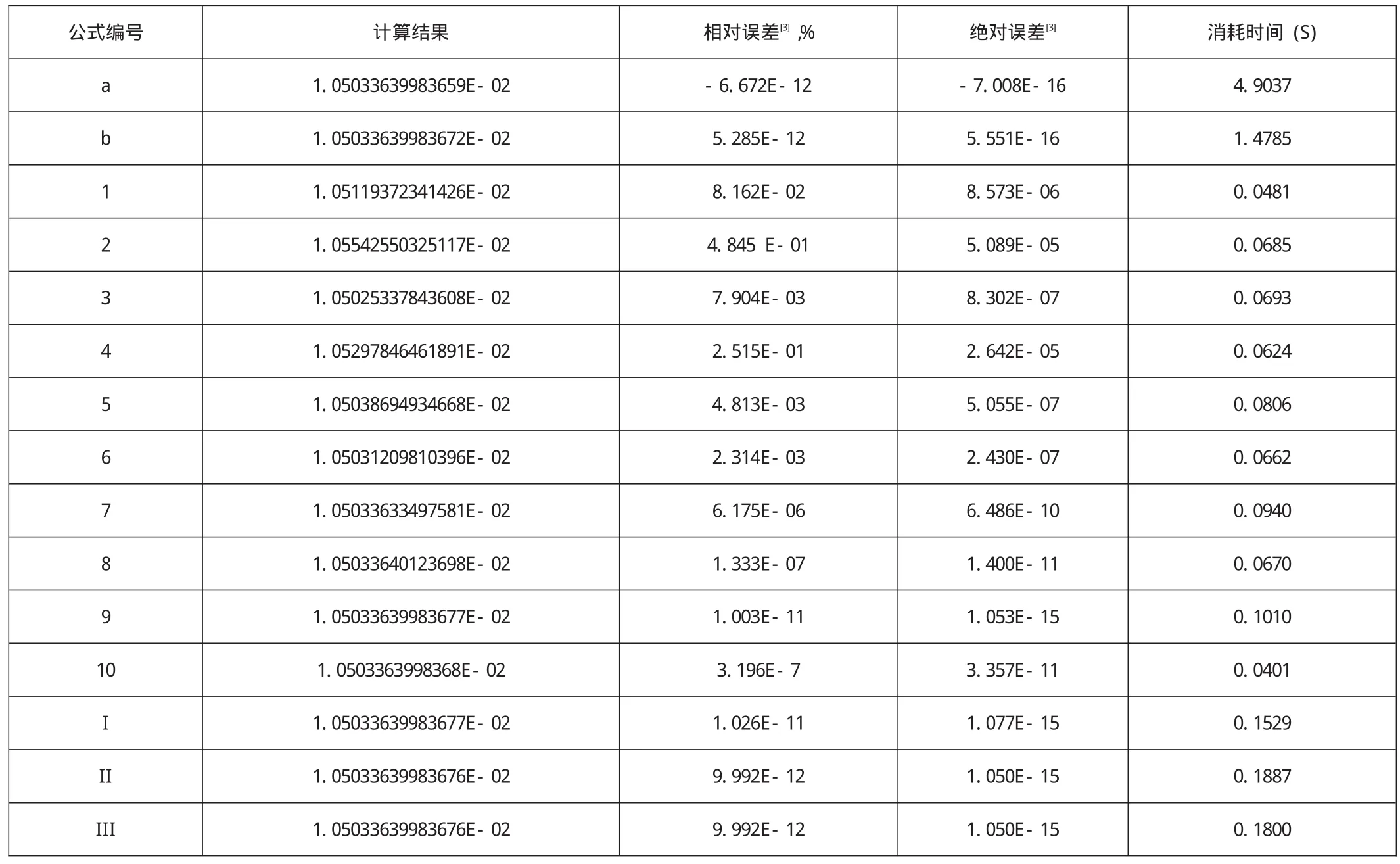
表4 摩阻系数计算参数对比
4.4 本文中的数值计算法可用来解决高次超越方程.
[1]Brown O G.The history of the Darcy-Weisbach equation for pipe flow resistance,In Environmental and water resources his⁃tory[J],Proceedings and invited papers for ASCE 150th Anniversa⁃ry(1852-2002),Fredrich,A.,and Rogers,J.,(eds.),ASCE,Reston,VA,34-43,2002.
[2]Coelho M,Carlos Pinho.Considerations About Equations for Steady State Flow in Natural Gas Pipelines[J],Braz.Soc.of Mech.Sci. & Eng.Vol.XXIX,No.3,2007.
[3]李庆扬,王能超,易大义.N数值分析[M].第三版.北京:清华大学出版社,2005.
[4]王小明.用反函数多项式展开法求解高次超越方程[J].温州职业技术学院学报2002,2(4):25-30.
[5]苑伟民,青青,袁宗明,等.Colebrook-white方程显式公式对比研究[J].石油与天然气,2010,28(4):5-7.
[6]苑伟民,贺三,袁宗明,等.VB与MATLAB混合编程在求解天然气无形参数中的运用[J].中国科学论坛,2008,8(9):21-23.
[7]张志涌.精通Matlab®6.5[M].北京:北京航空航天大学出版社2003.
[8]Michael Halvorson.Microsoft Visual Basic Professional 6.0 Step by Step[M].美国:微软出版社,1998.
[9]苑伟民,贺三,袁宗明等。求解BWRS方程中密度根的数值方法[J].天然气与石油,2009,27(1):4-6.
[10]苑伟民,贺三,袁宗明,等。BWRS状态方程中压缩因子的数值方法[J].管道技术与设备,2009,16(3):14-16.
[11]苑伟民.Colebrook-White方程新的显式形式的再形成[J].NGO,2013,31(1):17-19.
