不同材料杆组成的均质四边形边框绕质心轴的转动惯量

鲍四元

(苏州科技学院土木工程学院，江苏苏州215011)



不同材料杆组成的均质四边形边框绕质心轴的转动惯量

鲍四元

(苏州科技学院土木工程学院，江苏苏州215011)

摘要：对不同材料杆组成的均质四边形边框，利用离散质点系统的质心公式确定均质四边形边框的质心位置。基于平行轴定理推导四边形边框绕质心轴的转动惯量公式。转动惯量的解析公式用四边形的4条边长、对角线长和对边夹角表示。已有文献的一些公式成为本文结果的特例，所用方法可进一步推广到求解其他边框图形绕质心轴的转动惯量。

关键词：刚体；边框;四边形；质心;转动惯量

0引言

物体的转动惯量是个经典问题。最近，不少学者对具有规则形状的物体的转动惯量进行了研究，如椭圆环[1]、旋转面[2]、分形物体[3-4]、四边形物体[5]、边框物体[6-7]等，文献[6]及文献[8]研究了任意均质三角形边框刚体绕质心轴的转动惯量。已有文献考虑的情况往往都是单一的材料，另外，至今尚未发现关于四边形边框刚体对质心轴转动惯量的文献。

本文对于更一般的推广结构，即不同密度均质四边形杆组成的边框刚体，建立直角坐标系，利用离散质点系统的质心公式确定均质四边形边框的质心位置，并尝试推导原体系绕质心轴的转动惯量公式。

1均质四边形边框质心位置的确定

如图1，设均质四边形边框A1B1C1D1的4条边长分别为A1B1=d,B1C1=a,C1D1=b,A1D1=c,对角线A1C1=e,B1D1=f，质量线密度分别为常量λa、λb、λc和λd，4条边的中点分别为A、B、C和D(即各边的质心)。

图1　 四边形杆边框的示意图

建立一个直角坐标系xOy，原点O可任意确定。设A1、B1、C1和D1的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)和(x4,y4)。由于4杆A1B1、B1C1、C1D1和D1A1都是均质的，故4杆质心的坐标分别为：

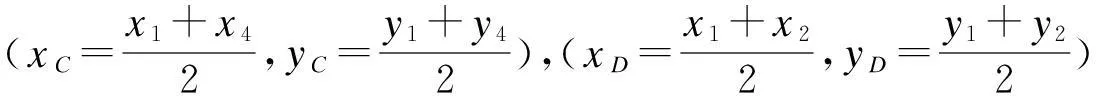
在A、B、C和D上分别放置质量为ma=λaa,mb=λbb,mc=λcc和md=λdd的4个质点,此4质点体系的质心G即为均质四边形边框的质心。由力学中离散质点系统的质心公式得质心G的坐标(xG,yG)为：

(1)

式中：M=ma+mb+mc+md。

将A1B1、B1C1、C1D1和D1A14杆质心坐标代入质心G的坐标，化简得质心坐标的一种表示：

(2)

2化简

化简ma(AG)2+mb(BG)2+mc(CG)2+md(DG)2

由勾股定理得：

(3)

为方便，记xij=xi-xj,yij=yi-yj(其中i,j表示图1中点的位置)，如式(3)中，xAG=xA-xG。由式(1)得

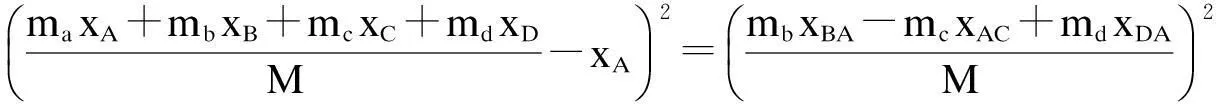
(4)

类似地，

(5)

故

ma(xAG)2+mb(xBG)2+mc(xCG)2+md(xDG)2=

(6)

式中：P=2xBAxAC+2xCBxBA+2xACxCB；Q=2xBDxDA+2xBAxAD+2xADxBA；R=2xCBxBD+2xBDxDC+2xDCxCB；S=2xADxDC+2xDCxCA+2xCAxAD。

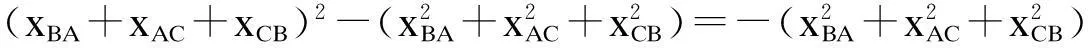
(7)

对Q、R、S可作类似处理，从而式(6)化为

ma(xAG)2+mb(xBG)2+mc(xCG)2+md(xDG)2=

(8)

类似地化简关于y坐标的表达式如下：

ma(yAG)2+mb(yBG)2+mc(yCG)2+md(yDG)2=

(9)

式(8)与(9)相加，并利用式(3)得

ma(AG)2+mb(BG)2+mc(CG)2+md(DG)2=

(10)

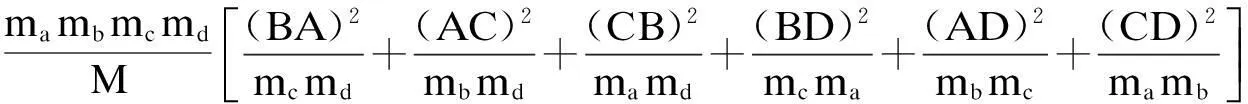
玉钺是良渚器物中最高贵的。它是权力的象征，根据权力的大小高低，钺的质地不同，有石钺，也有玉钺，只有王才能拥有最好的钺——玉钺。钺在中国古代也称之为戚，它本是一种武器，即斧头，陶渊明有诗云：“刑天舞干戚，猛志固长在。”后来，戚成为古代君王权杖。

图1中，由三角形中位线定理得BA=CD=f/2，AD=CB=e/2，又ma=λaa，mb=λbb,mc=λcc,代入式(10)得

ma(AG)2+mb(BG)2+mc(CG)2+md(DG)2=

(11)

3均质四边形边框对质心轴的转动惯量

设质心轴垂直于四边形所在的平面，由细杆对自身形心轴的转动惯量公式、平行轴定理及式(11)易得均质四边形边框对质心轴的转动惯量。

这里考虑4根杆的单位长度质量相等，即λa=λb=λc=λd=λ的情况。此时，均质四边形边框对质心轴的转动惯量为

IG=IaG+IbG+IcG+IdG=

(12)

考查2个特例。

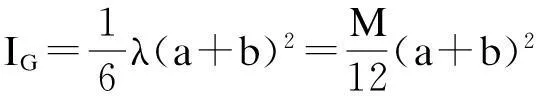
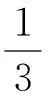
特例2是三角形杆框架系统。当d=0时，A1和B1重合，此时四边形边框A1B1C1D1退化为三角形A1C1D1(图3)。化简式(12)得三角形杆框架对质心轴的转动惯量

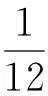
(13)

此结果与文献[6]及文献[7]中的结果完全一致。

图2　平行四边形杆边框的示意图

图3　三角形杆边框的示意图

4结论

1)任意四边形形状、不同材料杆组成的均质边框的质心在其中点四边形内，具体位置可由离散质点系的质心公式确定。

2)由式(10)知，各杆质量与其质心到边框质心的距离平方乘积的和恰好等于4杆中所有任选2杆质心点连线距离平方与这2根杆各自的质量三者乘积之和除以杆框架的总质量。

3)利用刚体转动惯量定义及刚体系质心坐标公式，可得不同材料杆组成的均质四边形边框绕过质心的垂直轴的转动惯量公式。当4杆质量线密度相等时，给出公式的解析形式。验算了2个特例情况：平行四边形杆框架系统和三角形边框系统。所得结果与已有文献结果完全一致，从而证明了本文结论的有效性。

[参考文献]

[1]赵新闻,周欣然,杨兵初.椭圆环刚体的转动惯量[J].大学物理，2008,27(6):13-14.

[2]楼智美.均质旋转面绕旋转轴转动的转动惯量[J].大学物理，2009,28(12):22-24.

[3]许佳敏，邱为钢.分形物体转动惯量的计算[J].大学物理，2011，30(11):53-55.

[4]鲍四元，汤亚娟.基于迭代法对分形物体转动惯量的研究[J].大学物理，2014，33(9)：11-14.

[5]周国全.任意四边形刚体平板绕质心轴的转动惯量公式[J].物理与工程，2002,12(6):24-26.

[6]周国全，徐斌富.均质边框三角形刚体绕质心轴的转动惯量公式[J].大学物理，2012，31( 12):8-9.

[7]李力.简捷推导均质三角形边框刚体绕质心轴的转动惯量[J].大学物理,2013,32(5)：19.

[8]孙徐莉,鲍四元.不同材料组成的均质边框三角形刚体绕质心轴的转动惯量[J].常州工学院学报，2014，27(5)：14-16.

责任编辑：唐海燕

本刊声明

为适应我国信息化建设，扩大本刊及作者知识信息交流渠道，本刊已许可中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库产品中，以数字化方式复制、汇编、发行、信息网络传播本刊全文。作者文章著作权使用费与稿酬本刊一并支付。作者向本刊提交文章发表的行为即视为同意本刊上述声明。中国学术期刊(光盘版)电子杂志社将免费提供作者文章引用统计分析资料。如作者不同意文章被收录，请在投稿时告知本刊，本刊将适当处理。

谢谢合作！

On the Rotation Inertia of a Rigid Quadrilateral Frame of Different Materials Round Its Centroid-through Axis

BAO Siyuan

(School of Civil Engineering,Suzhou University of Science and Technology,Suzhou 215011)

Abstract：By using the centroid formula of system of particles,the centroid of an arbitrary rigid quadrilateral frame made up of several materials is determined.Based on the parallel axis theorem,the rotation inertia of a rigid quadrilateral frame round its mass center axis is derived.The moment inertia of the rigid body is expressed by the edge length,the diagonal length,and the angle between the opposite sides of the quadrilateral frame.Some results in available literature have become the special cases of findings in this paper.The method in use can be further used in cases of other grid-like rigid bodies.

Key words：rigid body;frame;quadrilateral;centroid;rotation inertia

中图分类号：O313.3

文献标志码：A

文章编号：1671-0436(2015)04-0001-05

作者简介：鲍四元(1980—)，男，博士，副教授。

基金项目：国家自然科学基金项目(11202146)；江苏省“青蓝工程”优秀青年骨干教师资助项目

收稿日期：2015-01-22