过程功率谱熵在转子振动定量诊断中的应用
2015-12-21白广忱
白 斌,白广忱,李 超
过程功率谱熵在转子振动定量诊断中的应用
白 斌,白广忱,李 超
(北京航空航天大学能源与动力工程学院,北京100191)
针对旋转机械振动过程的复杂性和振动故障产生的随机性,提出了1种以信息熵理论为基础,通过多测点、多转速下的功率谱信息熵(功率谱熵)差矩阵来描述旋转机械振动过程变化规律的故障定量诊断方法。采用在转子试验台模拟转子振动的4种典型故障,得到4个测点多转速下的振动故障数据;对这些故障数据进行分析和处理,求其功率谱熵矩阵。结果表明:通过对转子振动故障信号进行实例计算和分析,该方法在转子振动故障分类和故障严重程度判断方面效果良好。
转子振动;故障诊断;信息熵;信息融合;功率谱熵;差矩阵;旋转机械
0 引言
转子不但是旋转机械的核心部件,还是其振动源和主要故障源。有时故障诊断要从定量角度根据故障的危害程度以及发展趋势而定。自20世纪80年代以来,基于振动的现代故障诊断方法得到了很大发展,但是,对于旋转机械,特别是大型复杂的旋转机械,其几何结构庞大且复杂,需要利用信息融合技术对多传感器的信息进行融合分析,以避免单个传感器采集信息分析出现的高几率虚警、漏报和混淆现象[1]。信息熵是对系统不确定程度的描述[2-5],是定量指标,可用于转子振动状态变化情况的定量分析。近几年,信息熵方法作为信息处理手段在国内外得到了长足发展,在医学、信息、航空航天、石油等领域得到广泛应用。澳大利亚新南威尔士大学的Endo等[5]应用最小熵解卷积技术来增强现有的基于滤波技术自回归模型,用于识别传动装置,特别是齿轮的局部故障;中国的徐可君等[6-8]提出基于Kolmogorov熵和Lyapunov指数能谱熵的航空发动机转子—机匣系统状态识别和故障诊断新方法;英国诺丁汉特伦特大学Yang等[9]提出采用结构熵检测信号中的故障特征;格拉斯哥大学的Li等[10]用Hubert光谱和信息熵进行内燃机故障诊断;西安交通大学的屈梁生等[11]将信息熵作为衡量设备可诊断性和可维护性的定量方法,用熵距来区分机械潜在故障类别;空军工程大学的李俊涛等[12]利用多元联合熵对航空发动机性能进行深入分析,为航空发动机及其他复杂旋转机械系统监控提供了1种新的方法。但上述均为基于状态的故障诊断方法,缺少对振动过程规律的描述。华中科技大学的陈非等[13]提出了基于过程的定量诊断方法,通过多测点多转速下的信息熵矩阵很好地描述了振动过程的变化规律;霍天龙等[14-15]将熵与SVM相结合对转子进行故障诊断;白斌等[16]将SVM进行改进对发动机转子故障识别,准确度得到提高。
本文基于信息融合思想,通过转子试验台模拟4种典型故障特征信号,以信息熵方法为基础,利用融合过程功率谱熵差矩阵对转子振动的故障类型以及故障严重程度进行定量诊断研究。
2 功率谱熵的过程定量诊断方法
2.1 振动信号的信息熵特征
信息熵最早是香农为解决信息的量化度量问题而提出来的,其基本概念为:假设M是可测集合类H生成的δ代数和具有μ(μ(M)=1)测度的勒贝格空间,且可表示为其有限划分A=(Ai)中互不相容集合的形
式中:μ(Ai)为集合Ai的测度,i=1,2,…,n。
对于转子振动频域信号,需要进行信息熵特征提取,进而求出功率谱熵。
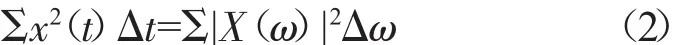
因此,S={S1,S2,…,SN}可以看作是对原始信号的1种划分。由此可以定义相应的信息熵,即功率谱熵(记作Hf,下标f表示频域)
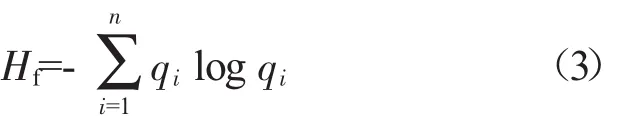
式中:qi为第i个功率谱在整个谱中所占百分比。
功率谱熵表征了单个通道振动信号的谱型结构情况。振动能量在整个频率成分上分布得越均匀,则信号越复杂,不确定性程度也就越大。对于转子振动故障诊断来说,由于缺少定量指标,单利用信息熵对转子故障进行诊断效果不太理想。在转子振动典型故障状态下,可以根据表征转子各系统状态的信息熵大小及其工作状态来判断是否有故障。然而,对于任意1种故障,由于采集振动波形的时刻和测点不同,计算得到的功率谱熵值有一定的分布区间。4种典型故障的重叠功率谱熵区域见表1,如果某一未知故障类型的功率谱熵值为1.0,就很难判断此类故障属于这4种故障中的哪1种。

表1 转子振动故障的功率谱熵分布区间
2.2 基于过程功率谱熵的定量诊断方法
假设功率谱熵矩阵A(M×N)是转子振动任意1种典型故障的诊断样本,其中M表示升速或降速过程中振动信号采样点数,N表示振动信号的测点数。矩阵A中的任意1个元素Aij就表示在第i个采样转速下第j个通道的功率谱熵值。对于未知故障类型的振动信号(即目标振动信号)进行同样的升速或降速数据采集,就可以得到M×N的功率谱熵矩阵B。为了比较功率谱熵矩阵B和A的过程规律,首先将2个矩阵相减求得功率谱熵差矩阵H

分别求功率谱熵差矩阵H的均值和方差矩阵
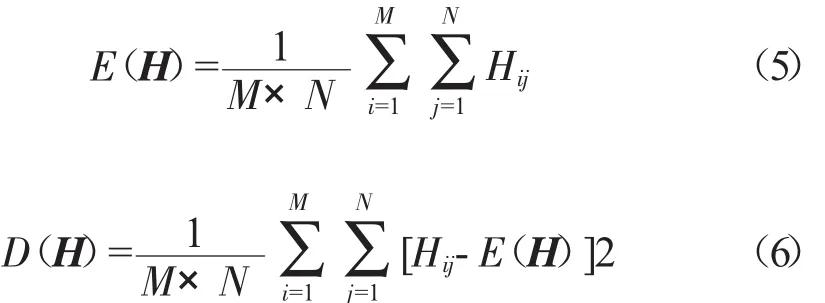
同理,可以求出目标振动信号与转子典型振动故障之间的功率谱熵差矩阵的均值和方差。通过求取其中均值绝对值和方差的最小值,就可进行故障判别。功率谱熵差矩阵的均值绝对值越小,表示目标振动信号的功率谱熵值分布区间与故障样本振动信号的功率谱熵值分布区间越接近,即目标振动信号属于这种故障的可能性越大,反之亦然。若目标振动信号的功率谱熵值分布区间与各故障样本振动信号的功率谱熵值分布区间都很接近,则就要通过信号功率谱差矩阵的方差值进行比较。功率谱熵差矩阵的方差反映了2种故障的相似程度,方差越小,表示目标振动信号的功率谱熵值的过程分布规律与振动故障样本功率谱熵值的过程分布规律越接近,即目标振动信号属于该故障的可能性越大,反之亦然。
3 转子振动故障模拟试验
转子升速过程是由很多状态构成的过程,在不同转速下,振动形态不同,按照转速间隔或时间间隔采集的振动波形记录了丰富的信息。1种故障在某一时刻或某一状态下引起的振动表现具有一定的分散性和随机性,但在1个过程中却有其规律性。多测点、多转速下的信息熵值组成的信息熵矩阵是多种状态的综合,这个信息熵矩阵反映了振动信号的过程规律。因此,可以通过信息熵矩阵来描述转子振动信号的过程规律。
转子试验台和试验测量系统如图1所示。为了研究转子振动的过程特征,在转子试验台上进行了4种典型故障(转子不平衡、轴系不对中、支座松动和转子碰摩)的模拟试验;每种故障都在1000~3000 r/min转速范围内来模拟,每种情况都分别进行多次升降速试验,振动信号采样的转速间隔设为100 r/min;试验系统布置了4个振动测点(测加速度),即4点振动信号,因此每次升降速试验能采集到每种故障模式的84组振动信号(1组振动信号对应某一振动测点的1个采样转速下的振动波形)来反映升速或降速的过程特征,进而对每种故障都可得到多个能反映其过程特征的原始数据集合。

图1 转子试验台及其测量系统
每组振动波形信号都可以求出上述的功率谱熵值,对任意1种故障,计算出最能反映其过程特征的那次试验的多测点、多转速下的功率谱熵值,得到1个以功率谱熵矩阵作为该种故障的故障诊断样本。
4 计算实例
4.1 转子振动故障功率谱熵矩阵计算
通过MATLAB编程对采样得到的各故障模式的振动信号进行计算,得到其功率谱熵矩阵。各种故障的功率谱熵值的分布区间见表1。对于任意1种故障,由于采集振动波形信号的时刻和测点不同,计算得到的功率谱熵值会在一定的数值范围内波动,有一定的分布区间。因此,仅仅依靠信功率谱值来进行故障诊断是行不通的。
4.2 目标信号选取和故障功率谱熵差矩阵计算
在相同试验条件下模拟的另外1次支座松动故障的3维图作为目标振动信号,如图2所示。
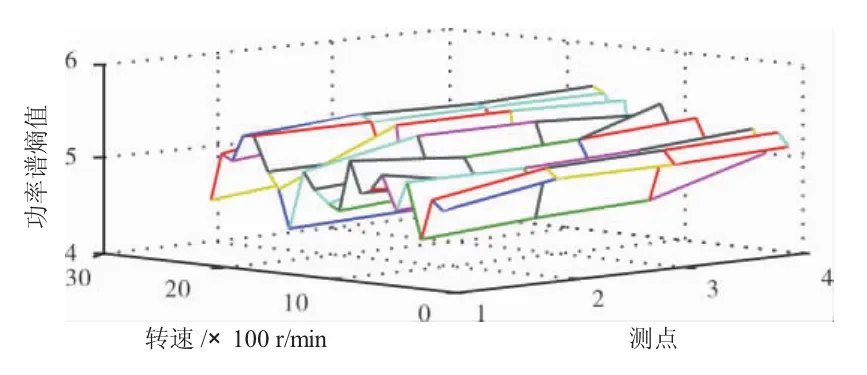
图2 目标振动信号的功率谱熵矩阵
把目标振动信号(图2)的功率谱熵矩阵分别与每种故障的功率谱熵矩阵样本相减,得到4个信号功率谱熵差矩阵,如图3~6所示。分别求得4个信号功率谱差矩阵的均值绝对值和方差,其结果见表2。
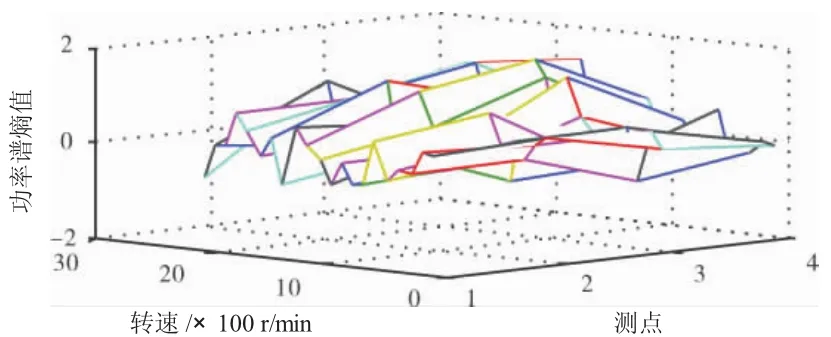
图3 与不对中故障的功率谱熵差矩阵
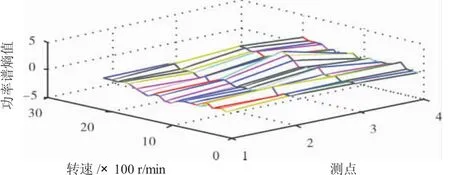
图4 与不平衡故障的功率谱熵差

图5 与碰摩故障的功率谱熵差矩阵

图6 与支座松动故障的功率谱熵差矩阵
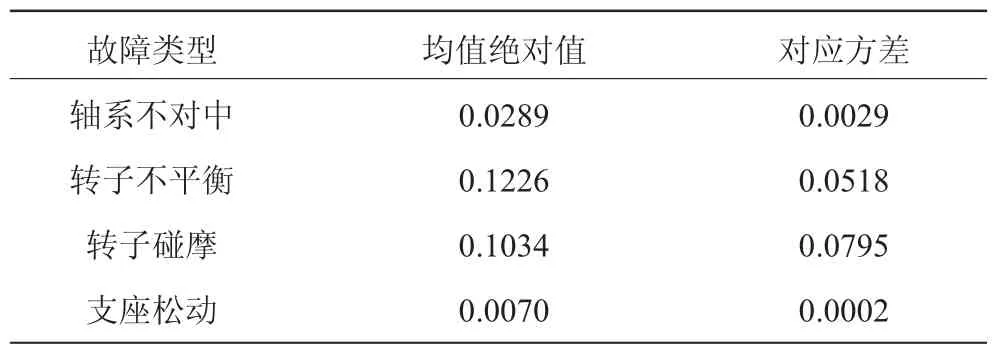
表2 功率谱熵差矩阵的均值绝对值和方差
从表2中可见,从相对应的4种故障功率谱熵差矩阵的均值绝对值来看,虽然可以诊断出目标信号的故障模式为支座松动,但由于均值绝对值的区别不太明显,故诊断效果不太准确。就其方差来看,目标故障振动信号与支座松动故障功率谱熵差矩阵的方差值最小,并与其他最小值相差10倍以上,即目标故障振动信号的信息值过程分布规律与支座松动故障的功率谱熵值的过程分布规律有较好吻合,故可以诊断为支座松动故障,与事实相符。
4.3 故障严重程度的诊断
为了用功率谱熵矩阵来诊断某种故障的严重程度,选取支座松动故障进行诊断,以转子正常工作状态(无故障模式)的振动信号为基准振动信号,功率谱熵矩阵用A表示。分别以1个和2个支座松动来模拟其松动故障模式,用其振动信号功率谱熵矩阵作为目标功率谱熵矩阵,分别用B1和B2表示相应2种故障矩阵。分别求H1=B1-A和H2=B2-A,并求B1和B2的均值绝对值和方差,其值的大小决定了故障严重程度,越大故障越严重;反之亦然。诊断结果见表3。
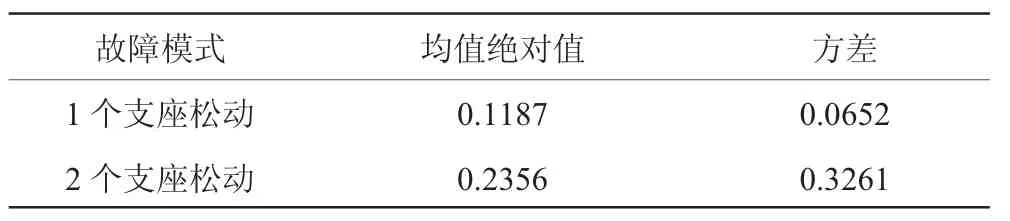
表3 故障严重程度诊断结果
从表3中可见,1个支座松动的故障模式的功率谱熵差矩阵的均值绝对值和方差明显比2个支座松动故障的小,说明1个支座松动故障模式的故障严重程度较小,这与假设相符。因此,利用功率谱熵差矩阵可以对故障严重程度进行有效判别。
5 结论
(1)本文以信息融合理论为基础,指出了基于状态诊断方法在大型复杂旋转机械诊断中的不足,提出了功率谱熵转子振动过程故障诊断方法。
(2)通过转子试验获取振动故障数据,从中得到转子振动过程信号变化规律的指标-功率谱熵矩阵,然后通过计算功率谱熵差矩阵的均值绝对值和方差,能定量地比较2次振动过程变化吻合程度,得到比较准确的过程规律的判别结果。
(3)基于过程融合功率谱熵的转子振动故障诊断方法能够很好地区分故障类别和判断故障的严重程度。
(4)由于大型复杂的旋转机械振动故障本身的复杂性,因而本文方法能否有效区分故障的发生部位,还需进一步研究。
[1]Nelson M,Mason K.A model-based approach to information fusion[J].Information,Decision and Control,1999(S1):395-400.
[2]黄献,宋治,郑文.功率谱熵对大鼠痫性发作预报的评估意义[J].中南大学学报,2009,34(8):776-780.HUANG Xian,SONG Zhi,ZHEN Wen.Effect of power spectral entropy on the prediction of seizure in epileptic rats[J].Journal of Central South University,2009,34(8):776-780.(in Chinese)
[3]毛鹏,王莉飞,成虎.基于信息熵的项目群管理组织结构研究[J].东南大学学报,2010,12(3):55-59.MAOPeng,WANGLifei,CHENGHu.A research of program management organizations on basis of entropy[J].Journal of Southeast University,2010,12(3):55-59.(in Chinese)
[4]胡军辉邵忍平曾泽君.基于谱熵的齿轮故障诊断方法研究 [J].机械传动,2007(5),84-87.HU Junhui,SHAO Renping,ZENG Zejun.Method of gears fault diagnosis based on spectral entropy[J].Mechanical Transmission,2007(5),84-87.(in Chinese)
[5]Endo H,Randan RB.Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J].Mechanical Systems and Signal Process,2007,21(2):906-919.
[6]余波,李应红,张朴.关联维数和Kolmogorov熵在航空发动机故障诊断中的应用[J].航空动力学报,2006,21(1):219-224.YU Bo,LI Yinghong,ZHANG Pu.Application of correlation dimension and Kolmogorov entropy in aeroengine fault diagnosis[J].Journal of Aerospace Power,2006,21(1):219-224.(in Chinese)
[7]徐可君,夏毅锐,江龙平.基于KolmogoroV熵的转子-机匣系统故障诊断研究[J].海军航空工程学院学报,2006,21(4):437-440.XU Kejun,XIA Yirui,JIANG Longping.Fault diagnosis research of ro-torcase system based on Kolmogorov entropy[J].Journal of Naval Aeronautical Engineering Institute,2006,21(4):437-440.(in Chinese)
[8]徐可君,江龙平.基于Lyapunov指数谱的航空发动机故障诊断研究[J].应用力学学报,2006,23(3):488-492.XU Kejun,JIANG Longping.Lyapunov exponent spectrum with application to aero engine fault diagnosis[J].Chinese Journal of Applied Mechanics,2006,23(3):488-492.(in Chinese)
[9]Yang W X,Hull J B,Seymour M D.Detecting the singularities in engineering signals[J].JournaI of Materials Processing Technology,2006,175(1-3):439-445.
[10]Li Hongkun,Zhou Pelin,Ma Xiaojiang.Pattern recognition on diesel engine working condition by using a novel methodology-hubert spectrum entropy[J].Journal of Marine Engineering and Technology,2005(6):43-48.
[11]Qu Liangsheng,Li Liangming,Lee Jay.Enhanced diagnostic certainty using information entropy theory[J].Advanced Engineering informatics,2003,17(3-4):141-150.
[12]李金涛,张凤鸣,李永宾,等.基于多元联合熵的航空发动机性能分析[J].微计算机信息,2007,23(1):53-54.LI Jintao,ZHANG Fengming,LI Yongbin.Performance analysis of aeroengine based on multi-joint entropy[J].Microcomputer Information,2007,23(1):53-54.(in Chinese)
[13]陈非,黄树红,张燕平,等.基于过程的旋转机械振动故障定量诊断方法[J].动力工程,2008,28(4):543-547.CHEN Fei,HUANG Shuhong,ZHANG Yanping,et al.A quantitative dagnosis method of vibration faults of rotating machinery based on process[J].Journal of Power Engineering,2008,28(4):543-547.(in Chinese)
[14]霍天龙,赵荣珍,胡宝权.基于熵带法与PSO优化的SVM转子故障诊断[J].振动、测试与诊断,2011,31(3):279-284.HUO Tianlong,ZHAO Rongzhen,HU Baoquan.Fault diagnosis for rotor systems based on entropy band method and support vector machine optimized by PSO[J].Journal of Vibration,Measurement and Diagnosis,2011,31(3):279-284.(in Chinese)
[15]费成巍,白广忱,李晓颖.基于过程功率谱熵SVM的转子振动故障诊断方法[J].推进技术,2012,33(2):293-294.FEI Chengwei,BAI Guangchen,LI Xiaoying.Method of rotor vibration fault diagnosis from process power spectrum entropy and SVM[J].Journal of Propulsion Technology,2012,33(2):293-294.(in Chinese)
[16]白斌,白广忱,林学柱.基于FSVM改良隶属度的发动机振动故障识别[J].振动与冲击,2013,32(20):23-28.BAI Bin,BAI Guangchen,LIN Xuezhu.Improved FSVM and multi-class fuzzy membership method for aeroengine vibration fault identification [J].Journal of Vibration and Shock,2013,32(20):23-28.(in Chinese)
Application of Process Power Spectrum Entropy in Rotor Vibration Quantitative Diagnosis
BAIBin,BAIGuang-chen,LIChao
(School of Energy and Power Engineering,Beihang University,Beijing 100191)
Aiming at the complexity of rotating machinery vibration process and the randomcity of vibration fault,a fault quantitative diagnosismethod whichdescribed thechangedisciplinarian of rotor vibrationby power spectruminformation entropy(power spectrumentropy)difference matrix under more measurement points and multi-speed based on the information entropy theory was presented.Four typical failures of rotor vibration were simulated based on rotor experiment and vibration fault data under more points and multi-speed were collected,and then the power spectrum entropy matrix was calculated through analyzing and processing the data.The result show that the validity of the method between distinguishing the rotor fault types and determining the fault severity is proved to be effective by example calculation and analysis of rotor vibration fault signals.
rotor vibration;fault diagnosis;information entropy;information fusion;power spectrum entropy;difference matrix;rotating machinery
V263.6
A
10.13477/j.cnki.aeroengine.2015.01
2013-07-15 基金项目:国家自然科学基金(51375032,51175017)资助
白斌(1984),男,在读博士研究生,研究方向为系统动力学、航空发动机结构振动及可靠性稳健性以及结构优化;E-mail:baibin@126.com。
白斌,白广忱,李超.过程功率谱熵在转子振动定量诊断中的应用[J].航空发动机,2015,41(1):27-31.BAIBin,BAIGuangchen,LIChao.Application of processpower spectrumentropy in rotor vibration quantitativediagnosis[J].Aeroengine,2015,41(1):27-31.
(编辑:沈广祥)
