基于聚类和拟合的QAR 数据离群点检测算法
2015-12-20王丽婧
杨 慧,王丽婧
(中国民航大学 计算机科学与技术学院,天津300300)
0 引 言
分析挖掘QAR (quick access recorder)数据[1,2]的主要目的在于找出其中包含的异常数据,从而发现一些有价值的存在于正常情况之外的其它情况。发达国家已经开始通过QAR 数据分析进行故障诊断,例如英国民航局的InsightFDM 系统根据对QAR 数据的处理来发现飞机维护计划之外的其它问题[3],美国开发的软件I-Trend利用QAR数据提高飞机的飞行安全。国内民航业对QAR 数据的利用还并不充分,目前主要应用序列相似性分析法[4]、小波变换[5]以及关联规则[6]等方法对数据进行研究,但是这些方法并不能对QAR 中出现的异常数据进行有效检测。
由于QAR数据所包含的数据量大、处理困难,所对应的离群点检测算法应该具有高计算效率和少量几遍扫描存储数据等特点。本文通过对QAR数据的分析,结合K均值聚类算法和最小二乘法提出了一种适用于QAR数据的离群点检测算法,为QAR数据在故障检测中的应用提供了前期准备。
1 相关工作
1.1 QAR 数据特点
QAR 数据是检修人员进行飞机维护,专家确定飞机故障的重要依据。其数据严格按照时间规律,采样频率为一秒一次。飞机发生故障时在QAR 数据上所表现出的主要是数值的波动和变化情况,飞机故障关注局部的变化,同时对数值比较敏感[7],且部分故障数据产生的时间是连续的。
QAR 数据记录的属性值数量巨大,但飞机的某一具体故障发生时,往往只与其中有限个数的属性有紧密关系。针对飞机故障的主要属性进行处理能够快速准确的对故障数据的产生进行定位,因此本文采用考虑主导因素的方法来提高算法检测故障的准确性。
1.2 离群点挖掘问题
从大量数据集中快速而且准确地找出飞机行驶过程中的异常数据并进行分析和判断,反映了离群点检测方法的时间效率和准确度[8]。
飞机发生某些故障时所对应的属性值比较集中,离散化程度较低,因此一些检测稀疏无规则离群点的算法[9]用于分辨QAR 离群数据效果并不理想。本文在基于距离的离群点定义的基础上,提出了一种新的算法实现对QAR 数据的离群点检测,相关定义请参见文献 [10]。
2 算法KLS介绍
针对QAR 数据的特点,算法KLS满足对QAR 数据离群点检测的如下要求:首先,为了及时发现飞机在飞行过程中隐含的问题,算法对QAR 数据的分析时间较短;其次,由于QAR 数据量大,算法对数据库的扫描只有一遍或者少量几遍,减少了时间和空间的开销。
2.1 算法相关原理
2.1.1 K 均值聚类
K-means聚类算法能够将大量数据分类聚合,有效处理大数据集,同时其迭代速度快,数据查找快速准确,因此在流数据中也得到广泛应用。文献 [11]在利用Kmeans算法对流数据进行处理时采用了按时间顺序分区聚类的思想。借鉴上述思想,算法KLS第一阶段对QAR 数据按照时间顺序进行分割并聚类,生成对应的K 均值点集。
QAR 异常数据发生时间较集中,同时发生故障时的数据关联性强,因此聚类生成的QAR 故障数据簇比较紧密且远离正常簇。根据这一特点,算法第二阶段忽略数据簇密度因素,利用生成簇的均值中心点来寻找离群数据。
2.1.2 最小二乘法
最小二乘法依靠样本数据寻找最优拟合,当数据依赖关系强且按照某种规律变化时拟合效果较好。
飞机在稳定飞行过程中,其各个参数都是按规律变化的,对QAR 数据聚类所得的均值点中包含大量的飞行正常数据均值参考点和少量的故障数据均值参考点,此时离群点对拟合效果的影响较小。算法KLS利用最小二乘法拟合参数曲线时,以实测值Yi与拟合值^Yi的差Yi-^Yi的平方和SQ 最小化来寻找最优模型
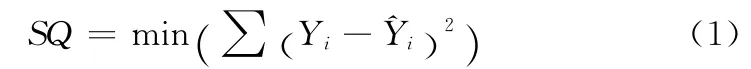
2.2 关键定义
假设QAR 数据被划分为数据块,每个数据块包含相同数目的数据点。按照数据流分区聚类算法对QAR 数据进行处理并进一步拟合寻找离群均值参考点的过程中,有相关定义如下:
定义1 对QAR 划分成的数据块分别进行聚类,每个数据块都生成k 个簇,每个簇的中心点为ct1,ct2,…,ctk,每个中心点的权重h1,h2,…,hk代表它所在的簇的数据个数,则每个数据块将由k 个均值参考点rei(cti,hi)所代表。
定义2 设均值参考点集为RE,对于每一个均值参考点rei,其中的中心点cti= (x1i,…,xni)所对应的离群因子pi定义为均值中心点到直线拟合点y= (y1i,…,yni)的偏差距离
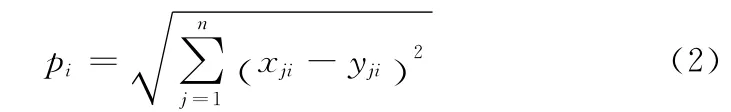
定义2将离群因子表示为两个值之间的欧氏距离,确保均值参考点距拟合线越远,所对应的离群因子的值就越大,距离拟合线越近,其离群因子的值就越小。
定义3 设离群因子集为P,那么属于离群因子集P的判定值AP 定义如下
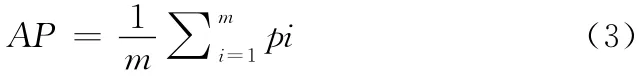
定义4 设离群程度为δ,离群因子最小值为min(pi),那么
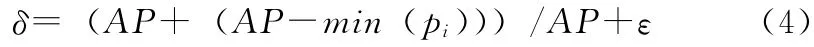
其中,ε为0到1之间的随机数。
定义5 对于离群因子集中任意pi∈P,若pi>δ*AP,则pi所对应的均值参考点rei为离群点,其所在簇中的数据即为离群数据。
从定义3可以看出,AP 值为所有离群因子总和的平均值,而定义4中离群程度δ值在离群点的判定中影响较大。由于符合离群点条件的均值参考点rei对应的离群因子pi的值远大于正常的离群因子值,设定的δ在依照离群因子最小值min(pi)和平均值AP 计算出的理想离群程度的基础上,加入随机数ε成为最终的离群程度δ,以确保少数离群因子值pi略高于理想离群因子范围的正常均值参考点与离群均值参考点的分离,保证了离群对象的获取。
2.3 算法实现
采用KLS算法对QAR 数据进行离群点检测大致分为以下两个阶段:第一阶段,将数据分区并进行聚类,找出均值参考点集;第二阶段,采用最小二乘法进行拟合,根据设定范围找出离群参考点,进而得到离群数据。QAR 数据量大,但其中所包含的故障数据是少量的,对数据划分之后利用K 均值聚类确保了聚类效果及速度,同时生成的均值参考点集中离群均值参考点个数也是极少量的,最小二乘法拟合几乎不受离群点影响,保证了算法的可行性。
算法输入:QAR 时序数据X,数据划分长度S
算法输出:QAR 中的异常数据
具体步骤:
步骤1 将输入的QAR 数据按照时间顺序每S 个数据点为一个长度区域进行划分,则当前输入数据可被划分为X= {X1,X2,X3,…,XM};
步骤2 对每个数据区域Xi内的数据按照k 均值聚类算法进行聚类,当中心点ctx(j)=ctx+1(j)(j=1,2,…,k),即聚类中心不再改变时,输出中心点值cti及其权重值hi,生成k个均值参考点 {re1,re2,…,rek},写入中心点集RE;
步骤3 重复步骤2,将每次生成的k个参考点按顺序依次写入RE,直至QAR 数据所有分区中的K 均值点全部产生;
步骤4 根据最小二乘法对步骤2中生成的均值参考点集RE 中各点的中心点值cti进行拟合,计算出当前飞机参数曲线模型;
步骤5 依据RE 中各点的中心点值cti= (x1i,…,xni),找出曲线模型中对应的拟合值y= (y1i,…,yni),按照式 (2)计算RE 中各个均值参考点rei的离群因子pi,写入离群因子集P;
步骤6 利用式 (3)计算离群因子集P 的判定值AP,同时找出离群因子集中的最小值min(pi),根据式 (4)计算出离群程度δ;
步骤7 在离群因子集P 中找到满足pi>δ*AP 条件的离群因子,组成离群集OP;
步骤8 找出OP 中所有的离群因子pi所对应的均值参考点rei,组成离群中心点集ORE,则其中的rei被视为离群点,其权重值hi的总和即视为离群数据的个数;
步骤9 扫描QAR 数据,找出ORE 中的rei所对应簇中的数据,这些数据作为QAR 故障数据或者干扰数据输出。
3 相关实验及结果分析
对文章所提出的KLS算法在飞机故障数据中的应用进行检测,算法采用MATLAB 7.0 实现,实验平台配置为Intel Core i5,2.5 GHz,4 GB 内 存 的PC,操 作 系 统 为Windows 7,通过某B737-800 型飞机记录的数据,对KLS算法用两种不同的故障类型进行实际检测验证,实验数据相关信息见表1。

表1 实验数据相关信息
实验一根据扰流板故障的特点,选用QAR 数据中的飞机高度和10号扰流板位置作为属性。在飞机飞行过程中,将飞机高度作为判断飞机飞行阶段的条件。根据专家经验,十号扰流板位置数值在-3 左右的时候视为正常。数据为飞机的一次飞行过程中记录的9184条QAR 数据值,其中扰流板故障数据有194条,取S=300,实验结果见表2。
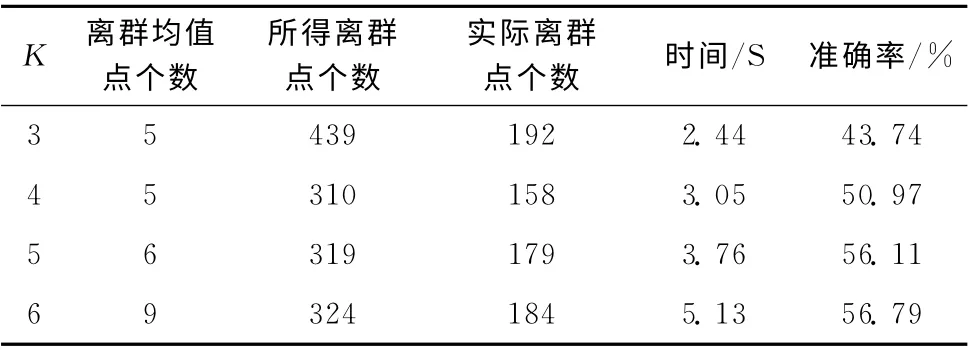
表2 扰流板故障算法效果
为了考虑K 值的选取对算法效果的影响,本文选择了4个不同的K 值分别进行实验以检测结果。从表2中可以看出,K 值较小时,对QAR 异常数据的检测比较准确,但同时对正常数据检测的准确率也相应较低。因为算法对数据比较敏感,受飞机高度的影响,当K 值较小时,所得离群中心点中包含有飞机故障数据,但同时也会把正常数据误划为异常数据;当K 值逐渐增大时,对故障数据准确的检测个数有所下降,但其中包含的正常数据相对减少,所以总体准确率增加,但还是有部分数据因为飞机高度的起伏变化而出现判断误差。
实验二选取的是空中颠簸的故障。由专家经验可得飞机在空中是否有空中颠簸的故障发生主要与飞机的垂直加速度的属性值有关,垂直加速度 (ALV)在大于1.5或小于0.5的时候颠簸感较强烈。由于空中颠簸的状况一般发生在飞机起飞之后,因此选取飞机的Air/Ground和垂直加速度为所用属性,并对Air/Ground 非数值属性进行预处理。数据为某航班飞机巡航阶段65521 条数据,其中含空中颠簸数据36条。取S=500,实验结果见表3。
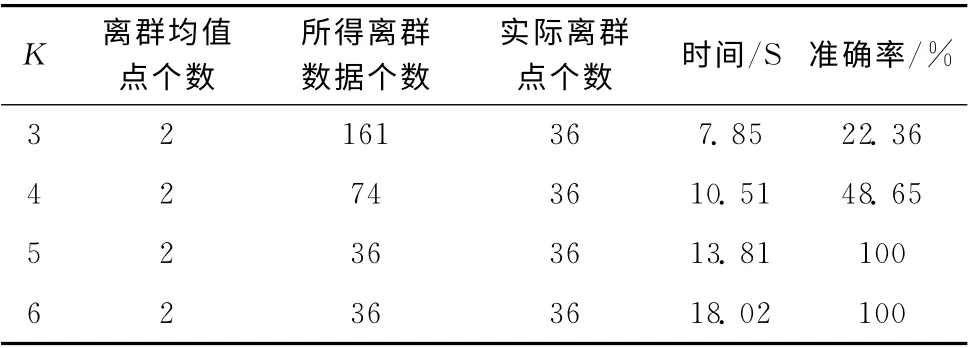
表3 空中颠簸算法效果
从表3可以看出,由于所选属性相对扰流板故障属性来说较为稳定,K 值较小的时候,生成的聚类簇个数较少,因此部分正常数据被划为了异常数据;但是随着K 值的增加,算法聚类效果增强,正常数据逐渐被排除,同时故障数据没有出现聚类偏差,因此离群点检测的准确率也随之增加。当K 值增加到一定程度之后,故障数据的聚类效果趋于稳定而不再发生变化。
由以上两个飞机故障的实验结果,得到算法在两个实验中所用时间的对比如图1所示。
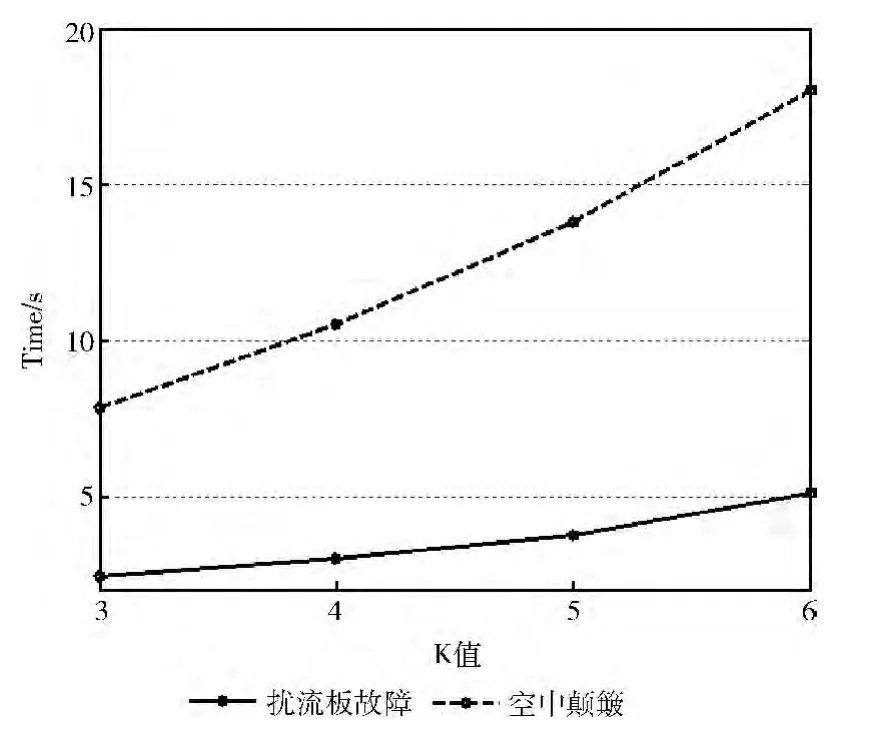
图1 算法运行时间
由图1可以看出,KLS算法在空中颠簸故障样本中的执行时间大于扰流板样本数据中的执行时间。分析可知由于空中颠簸故障样本数据集远远大于扰流板样本中的数据,同时空中颠簸故障样本数据分区所取S 值较大,因此其时间也相应增加。随着K 值逐渐增加,离群点检测耗费的时间也随之增加,因此在算法应用时,应该综合考虑时间和准确率等各方面的因素,选择合适的K 值,从而得到需要的检测结果。
4 结束语
本文针对QAR 数据参数稳定,故障数据聚类效果好的特点,提出了一种适用于QAR 数据的算法。该算法前期基于聚类对QAR 数据进行分区并利用K-means算法生成中间均值点,后期根据生成的聚类均值点进行最小二乘法拟合直线,通过计算均值点到直线的离群因子找出最有可能的离群点。算法的时间和效率都得到了有效验证,同时算法也满足了对QAR 数据少量扫描的特点,实验验证了该方法可行。
算法在应用中还需根据实际情况进一步改进来提高性能。比如在数据选取方面,应充分考虑如何有效地从QAR数据中选取各个故障具有代表性的精简属性。并且在考虑主导因素的同时加入次要因素的影响,使算法在故障检测中的应用范围更广泛。
[1]CAO Lin.QAR principle analysis and application in aircraft maintenance[J].Jiangsu Aviation,2011 (1):36-37 (in Chinese). [曹琳.QAR 原理分析及在飞机维护中的应用[J].江苏航空,2011 (1):36-37.]
[2]GAO Yuan.Research on fault early warning of B777airplane based on data mining [D].Tianjin:Civil Aviation University of China,2008 (in Chinese). [高原.数据挖掘算法在B777飞机故障预警中的应用研究 [D].天津:中国民航大学,2008.]
[3]Kiyak E,Caliskan F.Application of fuzzy logic in aircraft sensor fault diagnosis[J].International Journal of Systems Applications,Engineering & Development, 2012, 6 (4):317-324.
[4]YAN Wei,ZHAO Yang,GAO Yuan.Study on similarity search of flight time series data [J].China Computer & Network,2008,34 (21):54-57 (in Chinese). [闫伟,赵杨,高原.飞行时序数据相似性挖掘算法研究 [J].计算机与网络,2008,34 (21):54-57.]
[5]FENG Xingjie,LI Sheng,XUN Xiuxia.Civil aviation QAR data reduction and it’s performance analysis based on wavelet scaling coefficients [J].Computer Engineering and Design,2009,30 (5):1255-1258 (in Chinese).[冯兴杰,李胜,郇秀霞.基于小波尺度系数的民航QAR 数据约简及其性能分析[J].计算机工程与设计,2009,30 (5):1255-1258.]
[6]LIU Yang,CAO Huiling,LIANG Dajiao.The application of association rules mining in aeroengine QAR data[D].Beijing:Publishing House of Electronics Industry,2009:233-237 (in Chinese).[刘扬,曹惠玲,梁大教.关联规则挖掘在航空发动机QAR 数据中的应用 [D].北京:电子工业出版社,2009:233-237.]
[7]YANG Hui,ZHANG Guozhen.Similarity search for multidimensional QAR data subsequence [J].Computer Engineering and Applications,2013,49 (5):136-139 (in Chinese). [杨慧,张国振.QAR 数据多维子序列的相似性搜索 [J].计算机工程与应用,2013,49 (5):136-139.]
[8]XUE Anrong,JU Shiguang,HE Weihua,et al.Research of local outlier mining algorithms [J].Journal of Computers,2007,30 (8):1455-1463 (in Chinese). [薛安荣,鞠时光,何伟华,等.局部离群点挖掘算法研究 [J].计算机学报,2007,30 (8):1455-1463.]
[9]SUN Meiyu.Research on discords detect on time series based on distance and density [J].Computer Engineering and Applications,2012,48 (20):11-17 (in Chinese).[孙梅玉.基于距离和密度的时间序列异常检测方法研究 [J].计算机工程与应用,2012,48 (20):11-17.]
[10]XUE Anrong,YAO Lin,JU Shiguang,et al.Survey of outlier mining [J].Computer Science,2008,35 (11):13-18(in Chinese).[薛安荣,姚林,鞠时光,等.离群点挖掘方法综述 [J].计算机科学,2008,35 (11):13-18.]
[11]ZENG Ying,LUO Ke,ZOU Ruizhi.Outliers detection method based on K-means and agglomerative clustering [J].Computer Engineering and Applications,2009,45 (29):131-133 (in Chinese). [曾颖,罗可,邹瑞芝.基于K-均值聚类和凝聚聚类的离群点查找方法 [J].计算机工程与应用,2009,45 (29):131-133.]
