基于信息瓶颈的变压器故障诊断算法

路光辉，姬 波，雍明超，周 钟，牧继清

（1.许继集团有限公司，河南 许昌461000；2.郑州大学 信息工程学院，河南 郑州450001）

0 引 言

油中溶解气体分析 （dissolved gas analysis，DGA）是变压器故障诊断主要方法之一，可以对变压器故障做出有效诊断［1，2］。目前，业界主流应用的方法是基于规则的大卫三 角 形 法［3，4］，该 方 法 基 于3 种 油 中 溶 解 气 体：甲 烷（CH4）、乙烯 （C2H4）和乙炔 （C2H2）的数量进行运算并根据结果点在大卫三角形中的位置来判断故障类型。该方法具有简单、高效且直观地优点。除了基于规则的诊断方法外，近年来模式识别方法被广泛引入到变压器故障诊断问 题 中，如 人 工 神 经 网 络 （ANN）［5，6］、支 持 向 量 机（SVM）［7］、贝叶斯 （Bayes）方 法［8，9］和半 监 督 分类方 法［10］等都取得了一定的效果。信息瓶颈方法 （information bottleneck，IB）［11－13］是一种基于信息论的模式识别方法，被广泛应用于文档聚类［14］、图像分析［15］、DNA 处理和视频图像检索等领域，但是在变压器故障诊断领域尚未见到信息瓶颈方法的相关应用。其主要原因是信息瓶颈方法的主要研究对象是无监督分类 （聚类）问题，而不是有监督分类问题。因此，本文提出了一种基于信息瓶颈方法的变压器故障诊断算法。为了解决有监督分类的DGA 故障诊断问题，将基于信息瓶颈方法的DGA 故障诊断过程分为两个阶段。第一阶段进行无监督分类，即采用信息瓶颈方法对样本数据 （样本数据中含有训练样本和待测样本两类数据）进行聚类并得到多个结果簇，其目标是最小化簇内距离的同时最大化簇间距离；第二阶段进行结果簇内样本投票，即通过各个簇中训练样本的类标签进行投票，以简单多数或加权投票结果来给定待测样本的分类标签。在实际数据集上的实验结果表明，基于信息瓶颈方法的变压器故障诊断算法 （DGAsIB算法）是可行有效的，DGAsIB算法分类结果优于大卫三角形方法、BPNN 算法和Bayes方法。

1 变压器故障诊断方法

变压器运行中油中溶解气体主要包括氢气 （H2）、甲烷 （CH4）、乙烷 （C2H6）、乙烯 （C2H4）、乙炔 （C2H2）、Z烃 （ZTING）、一氧化碳 （CO）和二氧化碳 （CO2）等。变压器油中气体的含量在变压器老化及故障期会发生剧烈变化，各个气体的组份也会出现明显不同。因此，可以通过检测变压器油中溶解气体的组分来分析变压器运行状态并进行提前的预警。

1.1 基于规则的大卫三角形法

基于规则的DGA 方法包括大卫三角形法、IEC 三比值法、立体图示法等多种诊断方法。其中，大卫三角形方法（Duval method）由于具有简单、高效且直观的优点，成为了业界实际使用的主流方法。Duval法基于甲烷 （CH4），乙烯 （C2H4）和乙炔 （C2H2）的百分比进行运算，其值域范围为一个等边三角形。气体比例计算公式见式 （1）

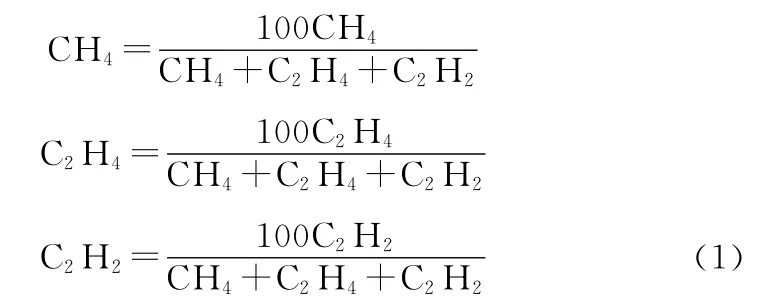
大卫三角形图示如图1所示。

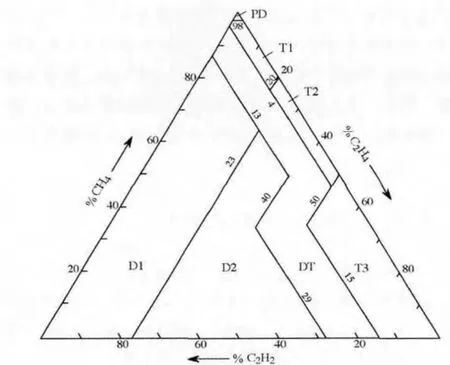
图1 大卫三角形

图1中交叉的实线构成了7个封闭区域。PD 区域代表局部放电；D1区域代表低能量放电；D2 区域代表高能量放电；T1区域代表低温过热 （T＜300℃）；T2区域代表中温过热 （300＜℃T＜700℃）；T3区域代表高温过热 （T＞700℃）；DT 区域代表放电及过热。Duval法通过对3种气体百分比的计算并投影为图中的坐标点，根据坐标点在大卫三角形中的区域不同来区分不同故障。

1.2 基于模式识别的人工神经网络法

研究结果表明，针对变压器故障DGA 识别问题，含有单个隐含层的BPNN 网络可以良好的满足诊断的要求。因为该网络已被证明可以逼近任意闭区间内的连续函数。含隐含层的三层BP神经网络的结构如图2所示。

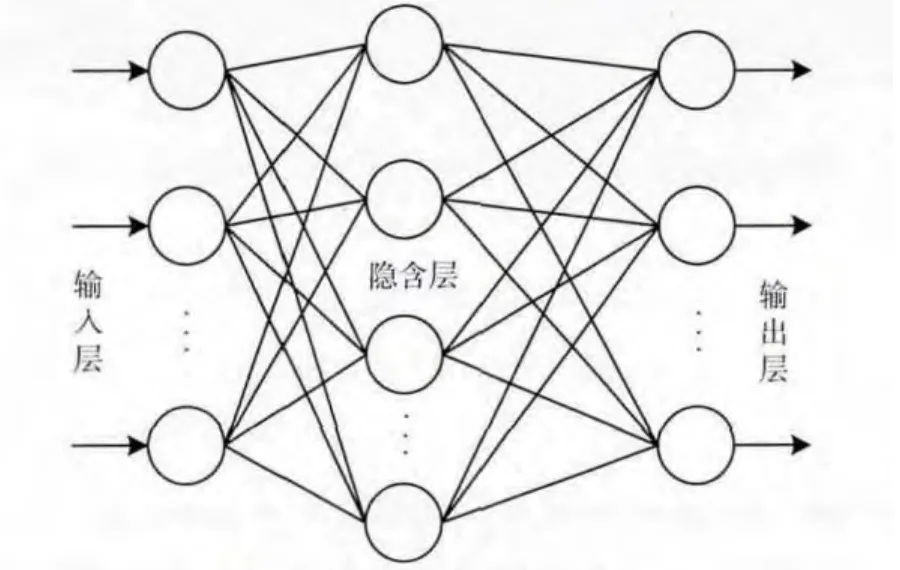
图2 BP神经网络的结构

令N，L，M 分别为输入层、隐含层和输出层节点数目，i，j，k 表示输入层、隐含层和输出层的节点，ωji为输入层到隐含层的权重，ωkj为隐含层到输出层的权重，则隐含层节点输出Oj和输出层节点输出Ok可见式 （2）

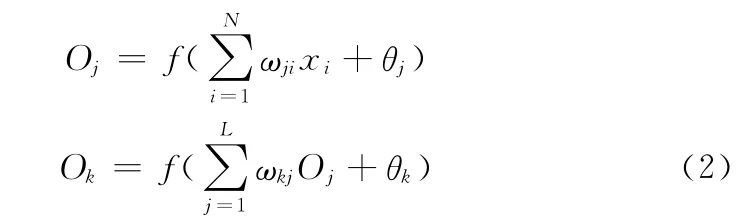
式中：f——激励函数，包括阈值型、分段线性型、Sigmoid函数和双曲正切型等；θj和θk为隐含层和输出层的阈值。

令输出层神经元的期望值为Ok′，则输出层误差函数E和权值的变化项Δωkj，Δωji见式 （3）

式中：η——学习速率。

1.3 基于模式识别的贝叶斯方法

贝叶斯方法根据已有样本数据判定待测DGA 数据的类别，即利用训练样本中的先验信息预测测试样本的后验概率。贝叶斯分类器具有较强的自学习能力，可以持续将新数据样本引入已知先验信息，从而提高事件后验概率预测的准确性。贝叶斯后验概率计算见式 （4）

式中：P（C｜X）为条件X 下C 的后验概率，P（C）为C的先验概率，P（X｜C）为条件C 下的后验概率，P（X）为X 的先验概率。

令A 代表DGA 属性变量集，C 代表DGA 故障类型变量。假设有n个条件属性变量，Val（Ai）1＜i＜m 代表属性取值范围，Val（C）代表DGA 故障变量取值范围，则A＝＜A1，A2，…，An＞，Ai的取值ai∈Val（Ai），C 的取值c∈Val（C）。令t代表训练样本，t＝＜a1，a2，…，an，cl＞，1＜l＜m，x代表测试样本，x＝＜a1，a2，…，aj，…，an＞。

样本x 归属于类cj的后验概率

式中：P（cj｜a1，a2，…，an）——测试样本为故障类型cj的后验概率；P（a1，a2，…，an｜cj）——故障类型cj下条件概率；P（cj）——故障类型cj的先验概率；α ＝1／P（a1，a2，…，an），α为常量。

2 基于信息瓶颈的变压器故障诊断算法

2.1 信息瓶颈方法

信息瓶颈方法起源于香农信息论，基于联合概率分布P（X，Y）对原变量X 进行压缩，在尽可能压缩X 的同时最大化地保存相关变量Y 的信息。该方法主要的研究对象是无监督分类 （聚类）问题，不要求预先获取训练样本中的先验知识，也不要求训练样本的存在。其目标函数如下

其形式解如下

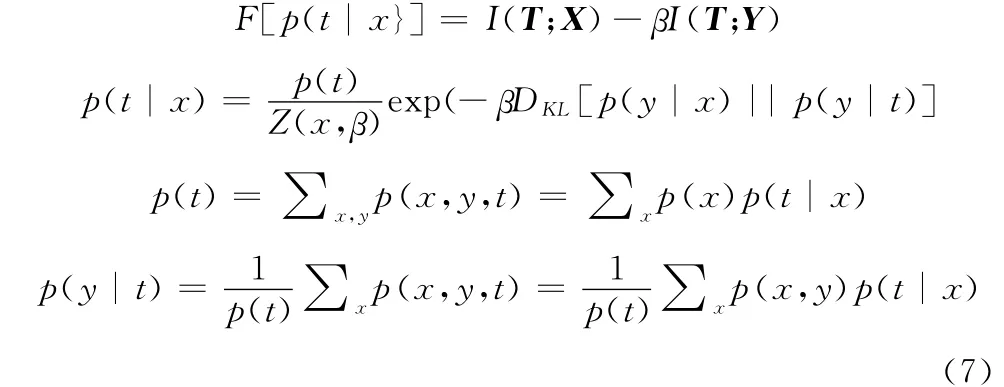
式中：Z（x，β）是归一化函数；DKL——KL距离。

序列化IB算法 （sIB算法）是一种广泛使用的基于信息瓶颈的序列化聚类算法。sIB算法属于划分聚类算法，要求已知聚类簇数目k，并初始随机将数据划分为k个簇。每一次迭代时从簇t中依次取出所有元素x，然后将x 重新分配到新簇tnew中，tnew＝argmincostt∈T（｛x｝，t）。

其中，cost（｛x｝，t）表示将x 指派到t引起的互信息I（T；Y）值的减小量；π1、π2为权值。

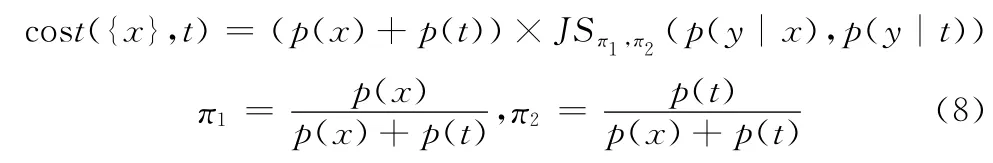
当所有元素x 均未被重新分配或达到指定迭代次数时sIB算法终止。

2.2 变压器故障诊断算法

信息瓶颈方法是一种无监督分类（聚类）方法，可以将数据按照相似性进行区分和类别归属，从而将样本数据集中的样本划分到若干个子簇中，使每个子簇代表一类样本。为了解决有监督分类的DGA模式识别问题，本文提出在将信息瓶颈方法应用于DGA诊断时，利用训练样本知识对聚类结果进行投票以获得最终的待测样本标号。诊断算法主要分为两个步骤：①采用IB方法对样本数据集（包括训练样本和待测样本）进行聚类，得到k个结果簇；②对于每一个待测样本，通过各个簇中训练样本的投票决定待测样本的类标号。

算法详细流程如图3所示。先取一个测试样本x，并将其合并到训练集中；接下来采用IB方法聚类并得到k 个结果簇；如果x 属于某个簇t，则使用该簇中所有训练样本进行投票。投票方式采用简单多数投票和加权投票两种方式。简单多数投票为简单多数选举方式，加权投票时以各个类别的先验概率为权来进行加权投票。例如，假设目标类c＝（1，2，3），先验概率Pc＝ （1／4，1／2，1／4）。如果结果簇A 中包含10个训练样本和1个待测样本，而10个训练样本的类标号为 ［1，3，2，1，1，2，1，2，2，1］。则该10个训练样本的简单多数投票结果为类标号1，即对待测样本标定为类属1。而加权投票结果为类标号2，即对待测样本标定为类属2。从中可以得出，简单多数和加权投票可以产生不同的类标号，而加权投票的可靠程度依赖于先验知识。

2.3 数据变换

在采用基于模式识别方法对DGA 数据进行诊断时，不同的算法有着不同的数据预处理要求。例如，神经网络算法要求对数据做归一化处理，以避免具有较大值域的属性左右算法结果；贝叶斯算法要求对连续数据进行离散化以便进行概率计算。对于IB 算法而言，要求数据为非负数据，以便能计算信息熵和互信息值并以此判定样本重新指派的代价。因此，本文算法实验中尝试性采用了一些数据变换方法来对数据进行预处理。根据DGA 数据特征，本文选择了Max－Min法、对数特征变换法和反正切函数法3种数据变换方法 （见式 （9））

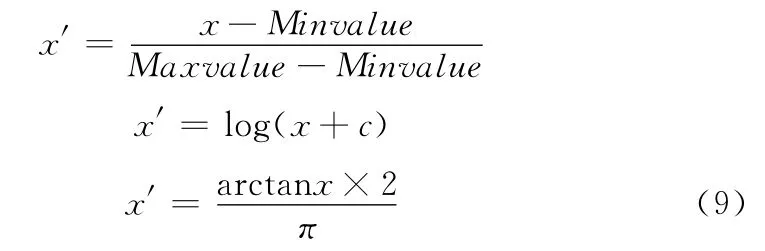
式中：Max－Min法变换后的值域为 ［0，1］区间；c是常数1.01，c常数的引入目的是为了将对数变换后的值域范围从 （－∞，＋∞）变化为 （0，＋∞）；反正切函数法变换后的值域为 ［－π／2，π／2］。

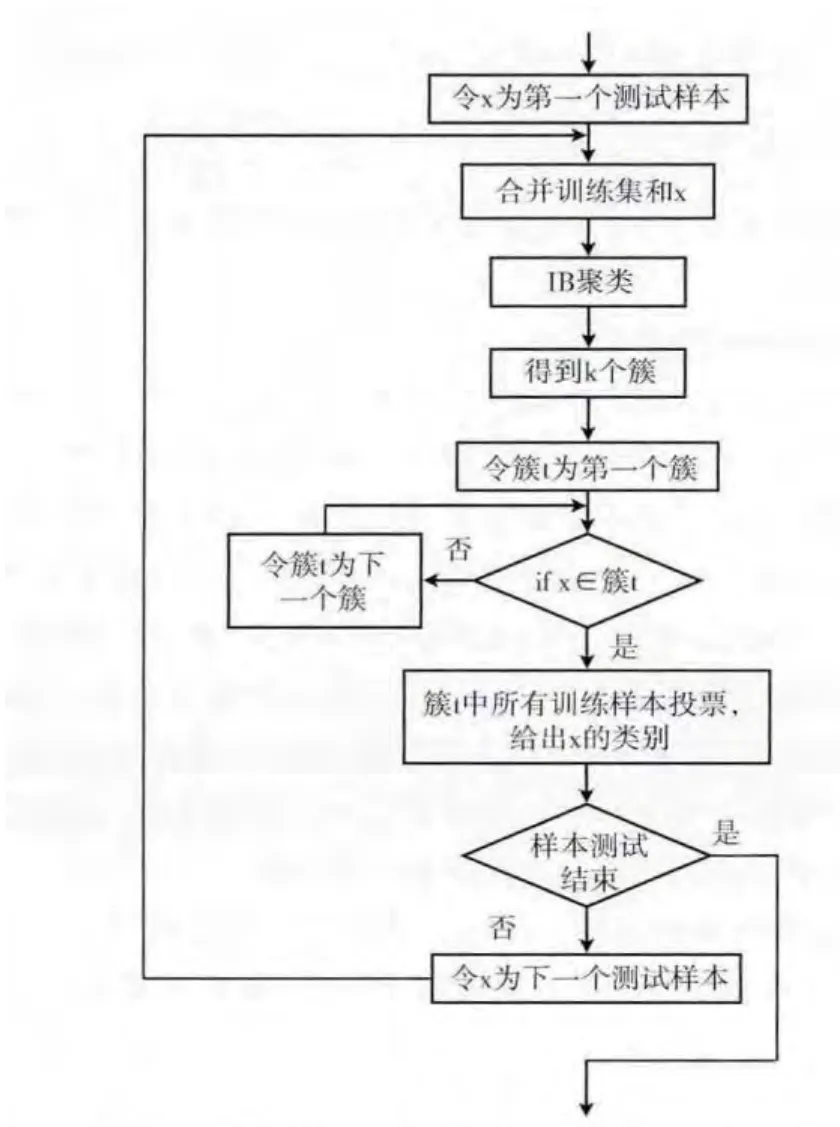
图3 基于信息瓶颈方法的DGA 诊断流程

?

2.4 诊断算法伪码

3 实 验

3.1 实验数据集

实验数据取自于实际生产数据，总共搜集到609 个样本。每个样本包括8 个属性 （H2，CH4，C2H6，C2H4，C2H2，ZTING，CO，CO2）和专家标定的数据类标号。数据清洗和规整步骤如下：

（1）删除没有专家标定的类别号的样本；

（2）删除重复样本；

（3）删除有缺失属性的样本；

（4）删除属性值为0的样本。最终得到的有效数据样本个数为350 个。数据样本的故障类型分布见表1。

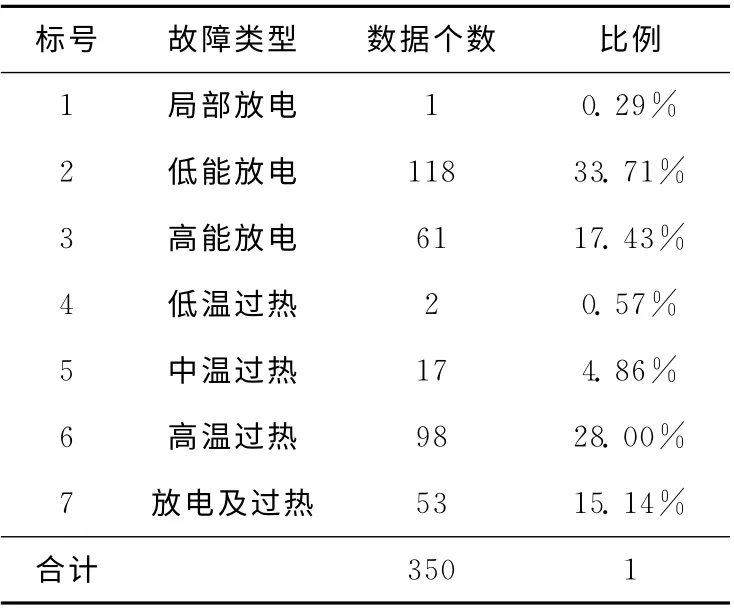
表1 数据样本的故障类型分布

针对这350个数据样本进行训练集和测试集划分后得到了10组实验数据集。划分方法采用十折交叉验证法，即将数据集随机分成十分，轮流将其中9份作为训练数据，1份作为测试数据。最终采用十次十折交叉验证正确率的平均值作为对本文算法精度的估计。

3.2 实验结果及分析

3.2.1 简单多数和加权投票结果比对

DGAsIB算法有3个参数，实验中类别k 设定为DGA故障类型数，即k＝7；聚类循环次数l＝10；平衡参数β＝＋∞。表2中给出了两种投票方式下原始数据、Max－Min变换后、对数变换后和反正切变换后的分类正确率。从中可以观察到：

（1）两种投票方式的对比中，10次实验中简单多数5次占优，加权投票5次占优，简单多数的十次十折平均值为58.37%，加权投票的十次十折平均值为57.83%。这说明简单多数投票法略优于加权投票法。我们认为，其主要原因是由于从实际生产中能获取的故障数据数目有限，导致各个故障类型的先验分布概率 （见表1）未能完全反映实际分布，因此加权投票法的权重值不够理想。随着数据的逐渐积累，应能改善加权投票法的结果。

（2）各种数据变换形式的对比中，仅有一次对数变换的结果最优。这说明对于IB方法而言，只需保证原始数据的非负性 （DGA 数据本身已具有非负的特性），而不需要其它模式识别算法要求的归一化或变换过程。

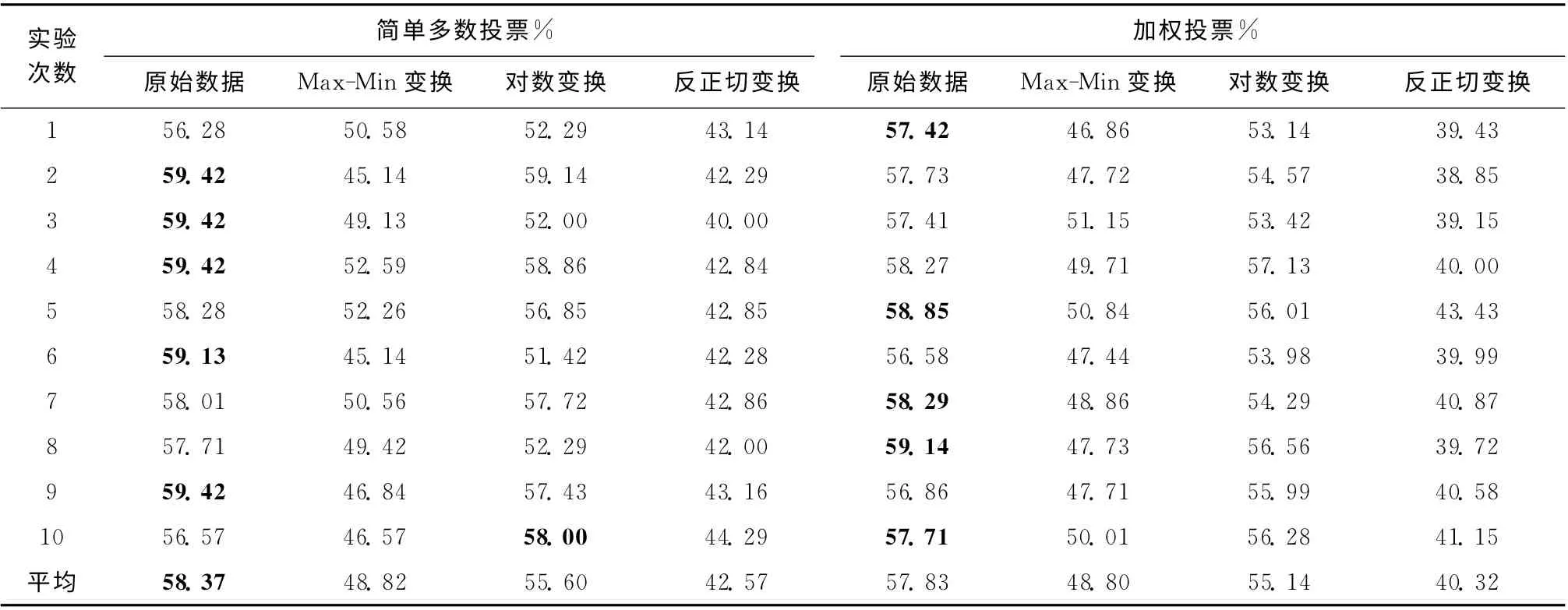
表2 简单多数和加权投票结果比对

3.2.2 DGAsIB算法和其它诊断算法比对

为了验证本文方法和算法的有效性，我们与业界应用的Duval法、以及基于模式识别的Bayes算法和BPNN 算法进行了比较。表3给出了DGAsIB 算法和其它诊断算法对比结果。图4中给出了各种算法的最优结果对比柱状图。其中，DGAsIB算法结果采用的是基于原始数据的简单投票结果。贝叶斯算法的离散化采用等宽离散方法，表中列Bayes＿2，Bayes＿3，...，Bayes＿5分别表示将各个属性值离散化为2～5箱后的Bayes分类结果。BPNN 神经网络的结构为3层，输入层8个节点，隐含层20个节点，输出层7个节点，激励函数选用tansig和purelin，网络训练函数选用traingdm。表中列BPNN＿0.01表示学习速率η 为0.01时训练的网络模型对测试集的分类结果，其它类似。从中可得如下结果。

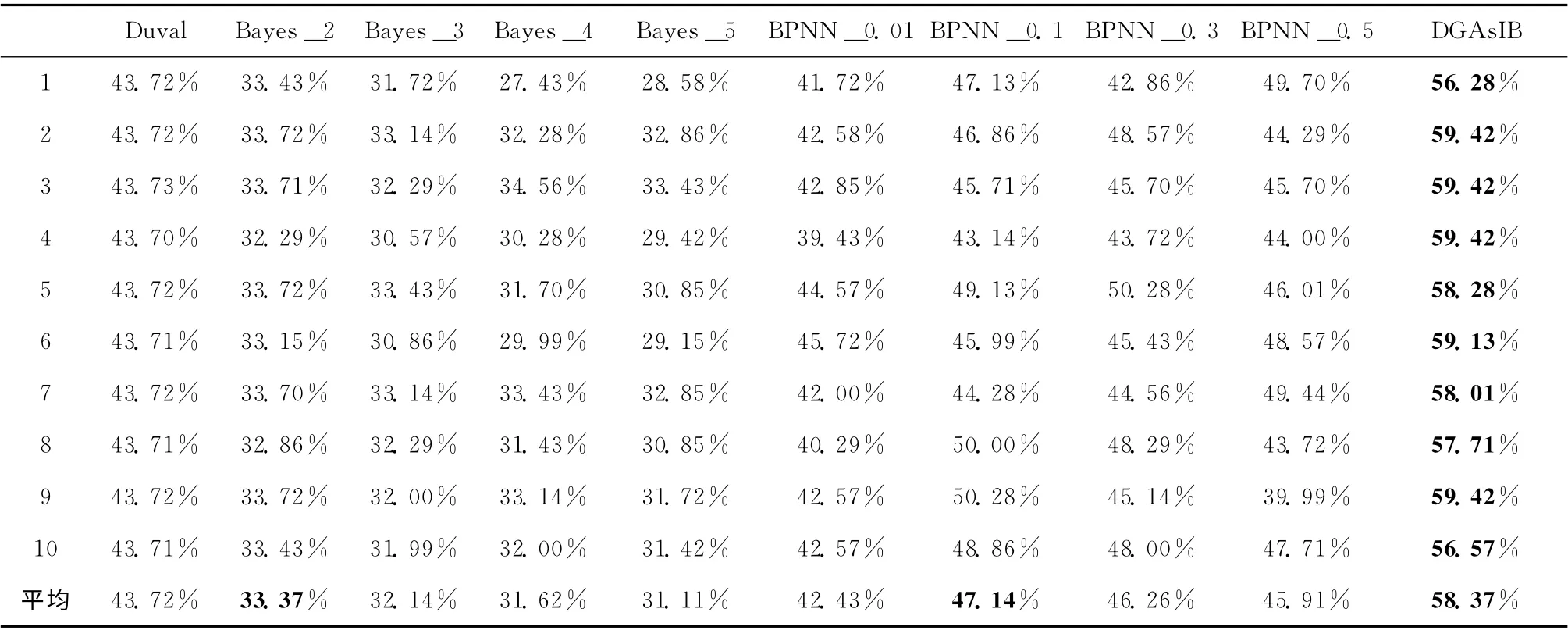
表3 DGAsIB算法和其它诊断算法比对

在参与比较的10种算法中，DGAsIB算法在十次十折实验中均为最优。DGAsIB 算法十次十折的总平均值为58.37%。比业界实际使用的Duval方法的43.72%提高了14.65%；比Bayes算法的最优结果33.37%提高了25%；比BPNN 算法的最优结果47.14%提高11.23%。这说明，基于信息瓶颈的DGA 诊断方法是可行的和有效的。

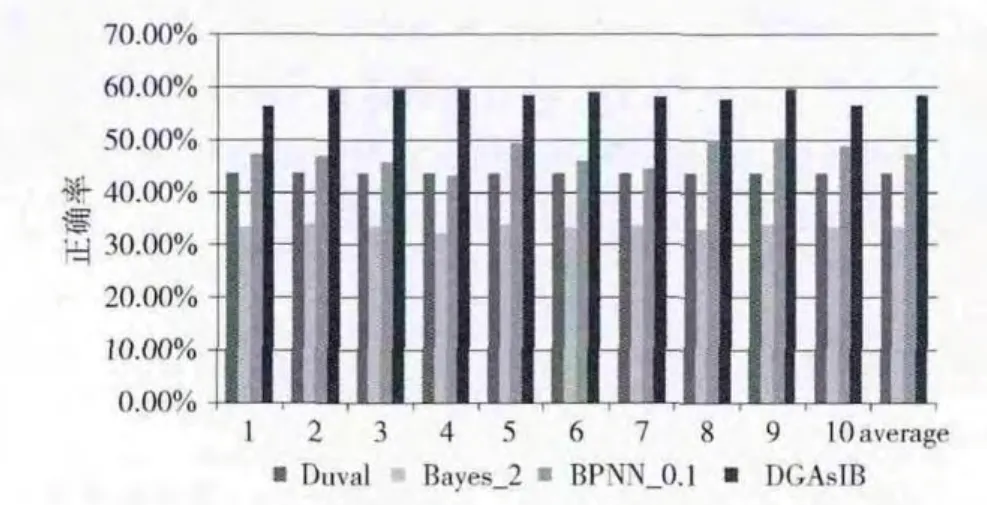
图4 各种算法的最优结果对比

4 结束语

本文提出了一种基于信息瓶颈方法的变压器故障诊断算法。该算法采用对DGA 数据进行聚类后的加权投票方式来判定待测样本的故障类别。实验结果表明，该算法应用到变压器故障诊断中，可以有效提高诊断的正确率，对于保证变压器的稳定性和电网的可靠性有一定意义。DGAsIB算法还有一些待完善的地方，如运算效率的提高和数据变换方法的改进等。这些工作涉及到了计算复杂度分析、数理统计等领域，将在后续工作中进一步改进。

［1］Bakar N A，Abu－Siada A，Islam S.A review of dissolved gas analysis measurement and interpretation techniques ［J］.IEEE Electrical Insulation Magazine，2014，30 （3）：39－49.

［2］HU Honghong，ZHENG Yajun，BAO Qitian.Analysis of online monitoring device of gases dissolved in transformer oil and its application ［J］.Transformer，2013，50 （4）：75－77（in Chinese）.［胡红红，郑亚君，包淇天.浅析变压器油中溶解气体在线监测装置及其应用 ［J］.变压器，2013，50 （4）：75－77.］

［3］YANG Zhenyong.Discussion on diagnosis of transformer fault based on“guide to the analysis and the diagnosis of gasses dissolved in transformer oil”［J］.Transformer，2008，45 （10）：24－26 （in Chinese）.［杨振勇. 《变压器油中溶解气体分析和判断导则》判断变压器故障的探讨 ［J］.变压器，2008，45（10）：24－26.］

［4］Sukhbir Singh MN，Bandyopadhyay.Duval triangle：A noble technique for DGA in power transformers［J］.International Journal of Electrical and Power Engineering，2010，4 （3）：193－197.

［5］Zakaria F，Johari D，Musirin I.Optimized artificial neural network for the detection of incipient faults in power transformer［C］／／IEEE 8th International Power Engineering and Optimization Conference，2014：635－640.

［6］ZHANG Juncai，QIAN Xu，ZHOU Yu.Application of extension neural network in transformer fault diagnosis［J］.Computer Engineering and Applications，2011，47 （7）：8－11（in Chinese）.［张俊彩，钱旭，周玉.可拓神经网络在变压器故障诊断中的应用［J］.计算机工程与应用，2011，47 （7）：8－11.］

［7］Wei C H，Tang W H，Wu Q H.A hybrid least－square support vector machine approach to incipient fault detection for oilimmersed power transformer ［J］.Electric Power Components and Systems，2014，42 （5）：453－463.

［8］BAI Cuifen，GAO Wensheng，JIN Lei，et al.Integrated diagnosis of transformer faults based on three－layer Bayesian network ［J］.High Voltage Engineering，2013，39 （2）：330－335 （in Chinese）.［白翠粉，高文胜，金雷，等.基于3层贝叶斯网络的变压器综合故障诊断 ［J］.高电压技术，2013，39（2）：330－335.］

［9］Su H S.Transformer fault diagnosis method based on rough set and Bayesian optimal classifier［C］／／Proceedings of the 3rd WSEAS International Conference on Circuits Systems，Signal and Telecommunications.Zhejiang.China：WSEAS，2009：183－188.

［10］GUO Xinchen，SONG Qiong，FAN Xiuling.Transformer fault diagnosis based on semi－supervised classifying method［J］.High Voltage Engineering，2013，39 （5）：1096－1097（in Chinese）.［郭新辰，宋琼，樊秀玲.基于半监督分类方法的变压器故障诊断 ［J］.高电压技术，2013，39 （5）：1096－1097.］

［11］Fabrizio R，Nicola D M.Applying the information bottleneck to statistical relational learning ［J］. Machine Learning，2012，86 （1）：89－114.

［12］Gedeon T，Parker A E，Dimitrov A G.The mathematical structure of information bottleneck methods ［J］.Entropy，2012，14 （3）：456－479.

［13］Slonim N.The information bottleneck：Theory and application［D］.Israel：The Hebrew University of Jerusalem，2002.

［14］Ye Y D，Ren Y L，Li G.Using local density information to improve IB algorithms［J］.Pattern Recogn Lett，2011，32：310－320.

［15］Dhanalakshmi S，Ravichandran T.A modified approach for image segmentation in information bottleneck method ［J］.International Journal of Advanced Research in Computer Engineering ＆Technology，2012，1 （7）：59－63.