面向片区的液化石油气库存预测模型

滕少华，邱小斌，张 巍，刘冬宁，梁 路

（广东工业大学 计算机学院，广东 广州510060）

0 引 言

液化石油气从购买、运输到使用，有一定的时间间隔，合理的存气量是必要的。在满足居民用气要求的前提下，降低各个气站的存气量是降低风险，减少成本，是提高企业运营效率的必然选择［1］。

当前液化石油气用户中，存在大量机械表用户，对于这些用户需要抄表人员入户抄表，抄表后才可以进行银行代扣费，这就存在着入户抄表率低、回款速度慢的问题。统计显示，一次抄表成功率只有30%，在扣款成功率只有80%的情况下，由此原因造成的煤气款项滞纳累计达到每月600万左右 （以某市为例）。因而，开展液化气库存预测对经营企业有重要意义。

考虑到居民用户液化气的使用受季节、气候影响，随时间、季节而变化，具有周期波动异常等特性，单纯的某种分析方法 （如回归分析）难以模拟并解决这类复杂问题，尤其是难以对一些潜在风险进行评估。

当前，许多液化气相关企业对下一阶段液化气储气量的预测仍依赖于管理人员的经验，少部分企业采用了一些统计分析方法，但都难以准确刻画居民用户液化气使用的上述特性。

时间序列是根据时间顺序得到的一系列观测值，在一个时间序列中，观测值之间有很大的相互依赖型，居民用户的使用情况符合这一特征，它的预测则是利用时态数据库［2］中历史数据来训练模型，预测事物将来的数据值以及发展趋势，常用的预测模型有：指数平滑法 （ES）［3］、求和自回归移动平均法 （ARIMA）［4］、季节性的指数平滑法（SES）［3］和 季 节 性 求 和 自 回 归 移 动 平 均 法 （SARIMA）［4］模型。

迄今，时间序列的预测研究已被运用到检测网络入侵［5］、伊朗地区水资源的需求量预测［6］等诸多领域。除了单独用ANN 来对时间序列进行预测外［7］，部分学者也将ARIMA 与ANN 结合起来使用［8］，Riquelme等也提出利用PSF模式对西班、美国、澳大利亚三地的电力市场价格和需求量进行预测，并取得了实际效果［9］。

上述研究从应用出发，各种方法对实际问题的缓解、解决起到了较好的效果，但研究也表明，尚未有一种模型对所有应用都适用。对不同数据集，由于数据的特性差异，各种模型有不同的表现。其中，指数平滑法及其季节模型要求数据集具备更好的完整性，ARIMA 及其季节模型对波动大的数据集具有更好的短期预测效果，但二者没有特别明显的界限；人工神经网络从生物仿生学中发展而来，具有较强的鲁棒性、记忆能力、非线性映射能力以及自学习能力［10］，且在该问题域的应用上，神经网络对提高部分精度也有不俗的表现，但过于复杂，计算时间过大，存在过学习等问题。

由于当前数据集中部分用户用气历史不够长，存在数据不完备的情况，因此，本文从片区出发，采用对波动大的数据集有较好效果的SARIMA 模型对片区液化气使用情况进行建模，预测片区储气量，并用液化气使用数据进行了检验，验证了SARIMA 模型对局部区域储气量的预测具有96%的准确率。最后将SARIMA 模型与指数平滑法、BP神经网络［11］和小波神经网络［12］进行了比较实验，实验结果表明，在片区液化气储量预测上，SARIMA 模型具有更好的预测效果。

1 居民用户液化石油气预测建模

1.1 SARIMA模型

ARIMA 模型也称为Box－Jenkins方法，它包含3 个子模型：自回归模型 （AR），移动平均模型 （MA），自回归移动平均模型 （ARMA）［4］。ARIMA 模型未考虑数据的季节性变化规律，对数据从整体上建模，在ARIMA 模型基础上加上对季节因素考虑的模型称为SARIMA。

季节性求和自回归移动平均模型 （SARIMA）的形式化 表 示 为［4］

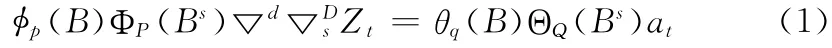
式中：at—— “白噪声”序列，s——时间间隔，季节性差分算子 s ＝1－Bs，p——趋势自回归阶数，d——趋势消除需要差分的次数，q——趋势移动平均的阶数，P——季节性自回归的阶数，D——季节性消除需要差分的次数，Q——季节性移动平均的阶数。

1.2 预测体系结构

片区液化气使用情况预测主要包含：数据预处理、模型识别、建模、模型参数估计、模型检验、评估以及预测等，其体系结构如图1所示。

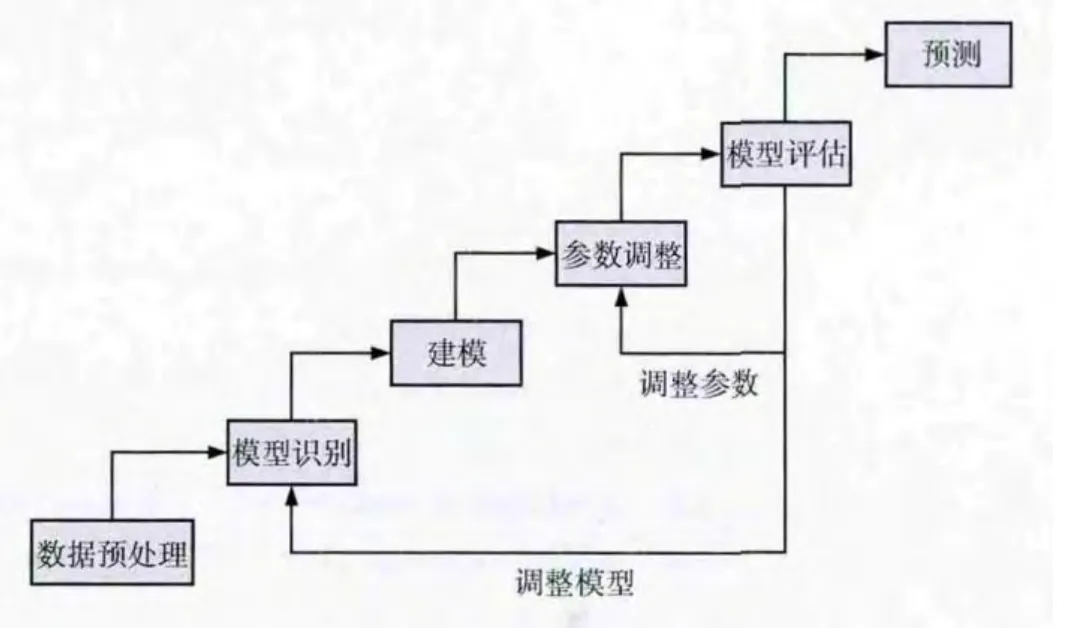
图1 片区液化气预测体系

图1中，模型识别主要是识别寻找可能的时间序列模型；参数调整则是在已识别模型的基础上调整、确定模型具体参数；模型评估，则是对当前模型进行 “过拟合”处理。若模型不符合，需对参数调整与模型识别进行反复迭代，迭代分为两种，一种是调整模型内的参数及其迭代；另一种则是从识别模型进行迭代，多次迭代后，可得到多个可行的模型。此时可借助贝叶斯公式 （BIC）在已识别的模型中选取最优模型，由此，并将它确定为最后预测模型。

由此可知，最终模型的确定是一个不断迭代选优的过程。

1.3 预测流程

模型识别是依据序列的平稳性，季节性，建立可能的预测模型；参数调整则是根据差分次数，差分后的自相关（ACF）和偏自相关图 （PACF）调整模型具体的参数值；模型检验，可通过检查建模后模型残差的自相关函数，判断是否为白噪声，其预测具体流程如图2所示。

对应预测流程，其伪代码如图3所示。

2 实验及结果分析

2.1 实验数据及预处理

本文的实验数据来源于某市居民用户4年中液化气的实际用气数据。

因为历史原因，燃气用户用气量历史数据存在缺失数据、各种噪声和不一致数据的情况。在数据分析前需要对数据进行预处理，本文中的数据预处理包括数据选择、数据清理、数据集成、数据变换、数据归约等［13］。

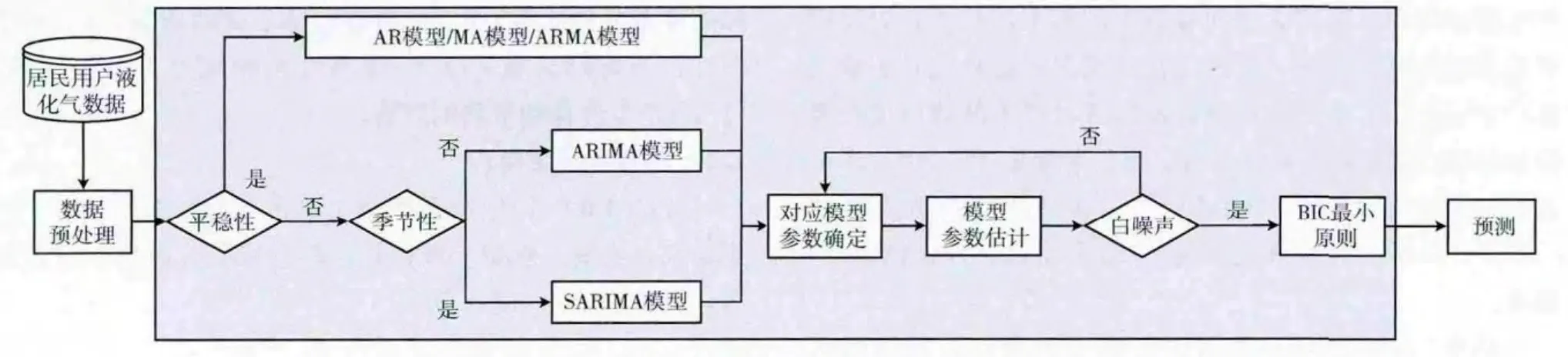
图2 片区液化气预测流程

由于用气数据以前未统一，数据来源于不同的系统，集成时造成少量数据丢失。另外，各个小区初始通气时间不一样，造成用气时间存在差异。对于用气时间不够长的小区，建模时可能导致训练数据不够，进而影响片区用气量预测模型的准确性。因此本文选取用气记录至少4年以上的片区用户数据进行建模。

具体实验时，此处选取某市北岭片区，对小区通气时间在2008年之前的用户进行建模。经统计，该片区共有4497户液化气用户，从2008年前开通点火至今一直在用气。

首先对用户用气数据序列进行异常检测［14］，对少数缺省值进行填充或修正，缺省值的填充根据用户历史数据以及发展趋势进行估计。由于燃气公司是每隔一个月上门抄表一次，因而抄表记录是跨月的，需要进行相应的拆分和合并，比如：抄表时间是2012－03－01至2012－04－06的用气记录，拆分成两条用气记录，分别是2012－03－01 至2012－03－31和2012－04－01至2012－04－06的用气记录，对于后一条记录还需要和四月份其它天数的用气记录进行合并，以形成2012－04－01至2012－04－30的一个月用气记录。此处分拆记录采用按天均分。某市北岭片区用气记录数据预处理后，共有用气记录296660条，形成本文的实验数据。

对于含有季节性的时间序列数据，按式 （2）形式化［4］

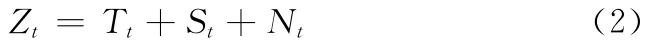
式中：Tt——趋势项，St——季节性，Nt——噪声（异常）。

2.2 实验及结果分析

图4是按照用户用气量构成的时间序列构成的图，由图4不难发现，每一年的用气量波形都相似，每一个波形的最大值和最小值有一个明显的上升趋势；每年6、7、8月份是一个低谷，每年12、1、2月份是一个用气量高峰期；这明显体现季节变化趋势，并且数据是不平稳的。由此可大概确定使用的模型是SARIMA （p，d，q）× （P，D，Q），数据的非平稳性需要通过差分来达到平衡，模型具体参数值则根据差分后序列的ACF、PACF中的拖尾情况确定。

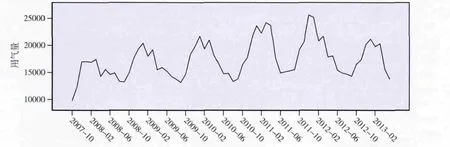
图4 北岭片区总用气量序列

差分的原则是进行最小差分次数且能保证平稳性，过多的差分虽然能保证序列更加平稳，但差分过多会导致样本损失，反而使模型不能反映实际数据。一般来说，取0、1、2中的一个差分，就可以满足问题所需。

在某市北岭片区用气量的时间序列中，对序列进行一阶差分以消除趋势增长，查看该序列是否达到平稳性要求。在图5中，图 （a）表明了d＝1的时间序列情况，数据都在0周围波动，序列基本达到平稳性；图 （b）是自相关函数图，自相关值大部分都在置信范围内，说明自相关性很弱，表明一次差分趋势不稳定性确实已经去除，另外在12的倍数节点上，数值一直很大，而且具有拖尾现象，这表明该序列确实存在季节性，而且间隔为12；图 （c）是偏自相关函数图，在K＝12处数值很大，这符合实际情况，一年之中各个季节，气候温度不一样导致用气量呈现着季节性质。可以看到偏自相关函数图在K＞12之后都截尾，而自相关是拖尾的，所以参数p可能取值12，研究结果表明，p的值一般是不大于2 的，p的值也可能是1、2，而q的值为0。

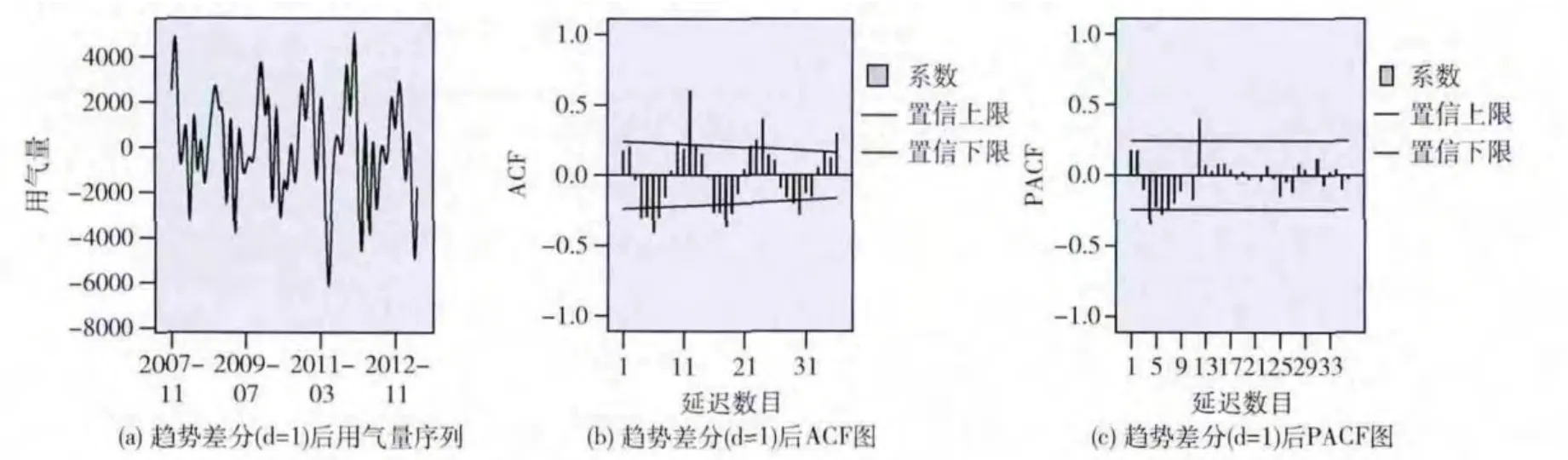
图5 趋势差分 （d＝1）后用气量序列、ACF及PACF图

在确定序列具备季节性趋势后，按照周期s＝12对原始用气量序列进行一阶季节差分，差分后序列如图6 （a）所示，序列在一阶季节差分后达到平稳状态，进而观察其自相关函数图和偏自相关函数图，此时在12 的倍数节点上，自相关函数值和偏自相关函数值在延迟s后都已经在置信区间范围内，也就是说都是截尾的，如图6 （b）和图6 （c）所示，因此p，q的取值都可能是0，1。另外注意到一次季节差分后的自相关函数在一定范围内持续为正或持续为负，说明还存在一定的相关性。

进一步对序列进行趋势差分和季节差分，其中d、D 都为1，观察差分后的序列，如图7 （a）所示。注意到在进行趋势差分和季节差分后，序列是平稳的，自相关函数图和偏自相关函数图也几乎都在置信度为95%的置信区间内，与此同时，自相关函数值也是正负交替，说明序列有必要将趋势差分和季节差分结合，如图7 （b）和图7 （c）所示。

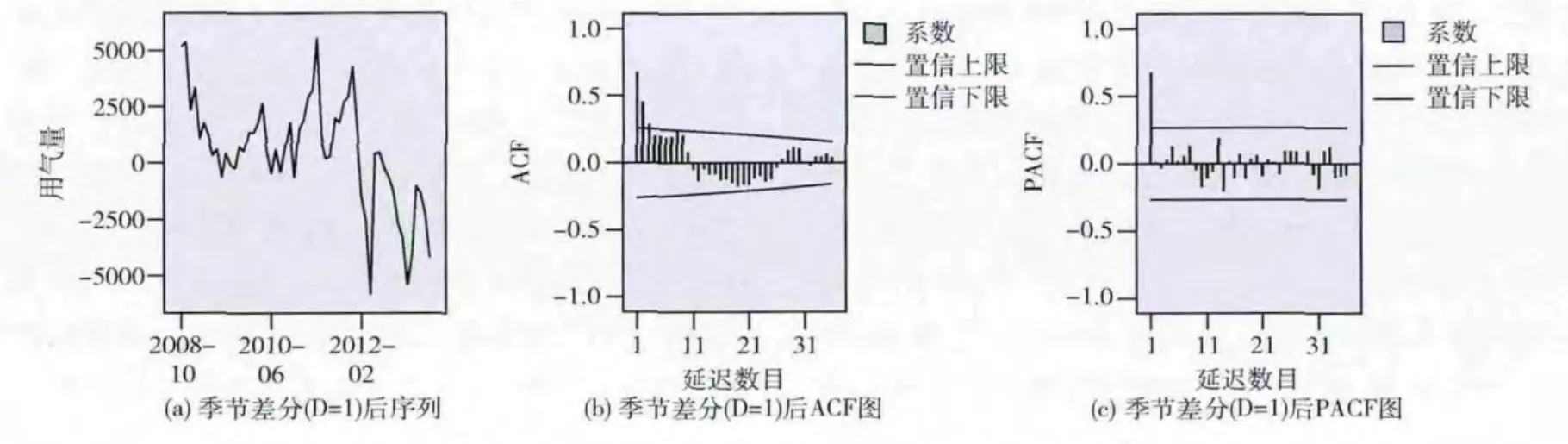
图6 季节差分 （D＝1）后序列、ACF及PACF图

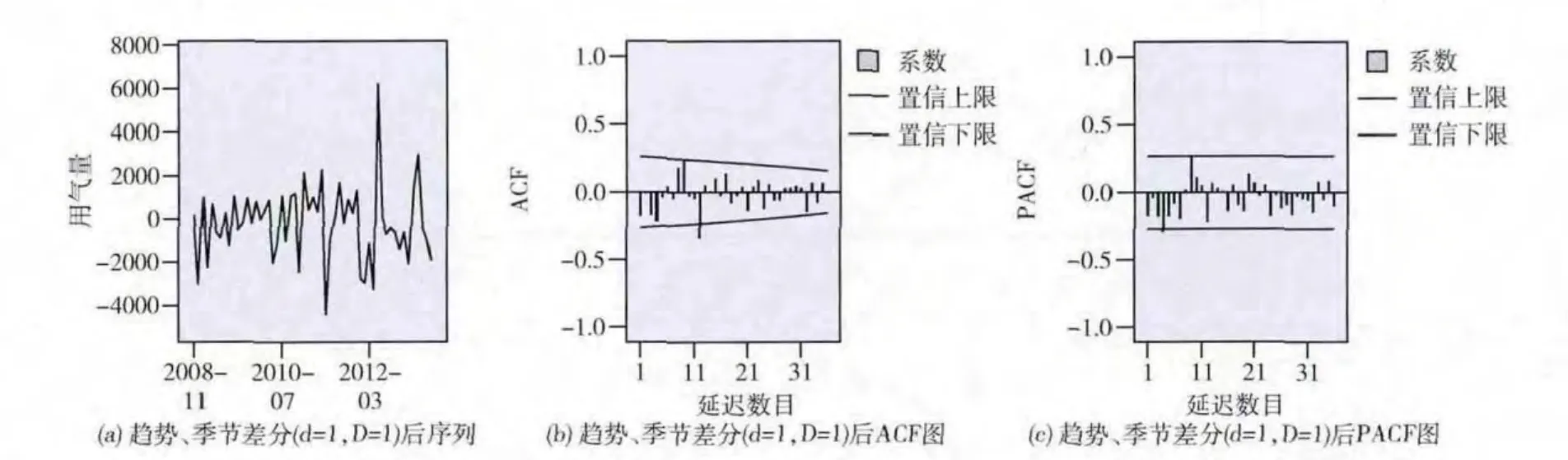
图7 趋势差分，季节差分 （d＝1，D＝1）后序列、ACF及PACF图

可用于识别的模型存在多个，我们并不知道哪一个模型是最适合的，这时可以通过查看候选模型的BIC 值，它表示序列模型之后相对 “真实模型”的信息损失，BIC 值最小的候选模型表示模型损失最小，但也不是最优模型，只是相对较优，BIC可表示为

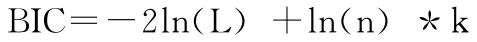
式中：L——在该模型下的极大似然函数，n——数据的数量，k——模型参数的变量个数。

候选模型以及BIC见表1。

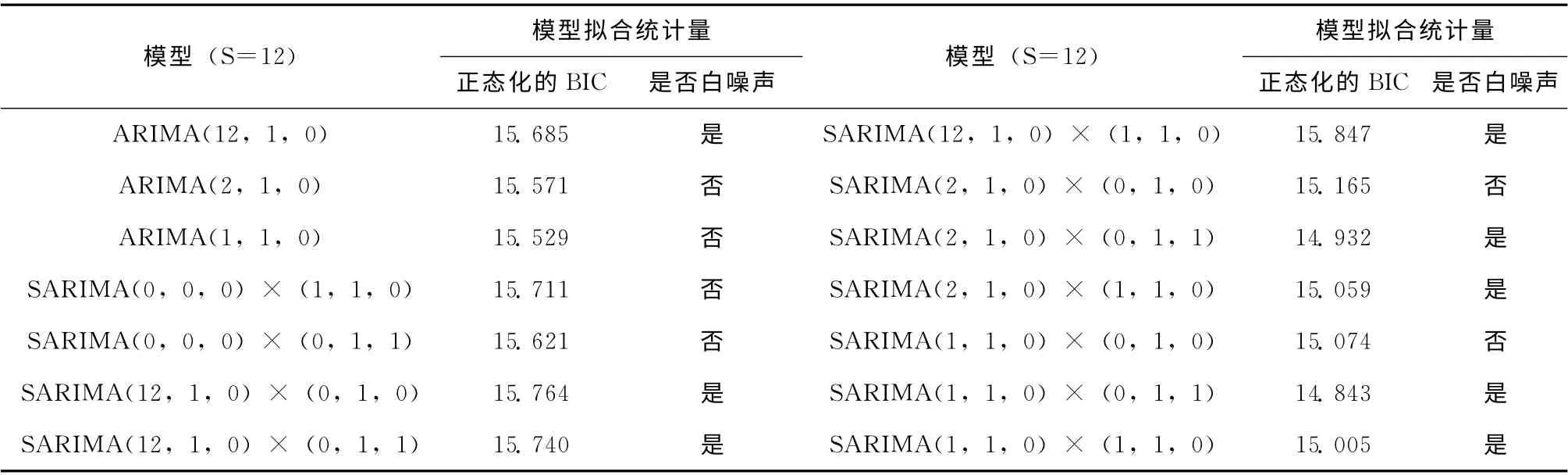
表1 候选模型及其BIC、白噪声

根据建立模型后的残差要符合白噪声原则，可以知道在单独的趋势差分后的模型和季节差分后的模型中，只有ARIMA（12，1，0）模型的残差是白噪声的，而二者结合的模型大部分都满足该原则，又基于BIC 最小原则，最后的模型确定为SARIMA（1，1，0）× （0，1，1），该模型的残差如图8所示，预测如图9所示。

从预测图中可以看出，序列的真实值都在置信范围内，特别是在2012年下半年以后，用气量相对以前有着较大的下降趋势，而该模型也能对这种变化进行合理的预测，表明了模型对该问题域建模有较强的健壮性。

在对2012年06月至2013年05月时间段内的用气量预测中，各模型都有不错的准确率，但是SARIMA 模型相对其它模型，具有更高的预测准确率，达到了96%，比指数平滑法、BP神经网络和小波神经网络更优，具体情况参见表2。但不可否认的是，当前数据集仅能提供年月，不能提供或者未使用其它影响用气量变化的因子，如温度、GDP、气价等，这对神经网络的训练带来了一定的影响，间接地影响了预测的准确性，各模型的比较如图10 所示，此时，SARIMA 模型相对于其它模型，其波动较小。

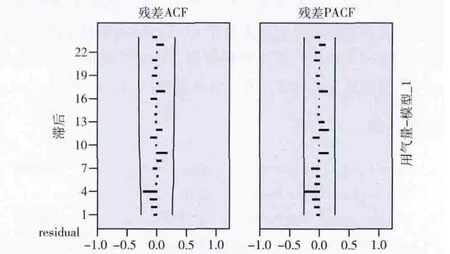
图8 SARIMA（1，1，0）× （0，1，1）模型残差

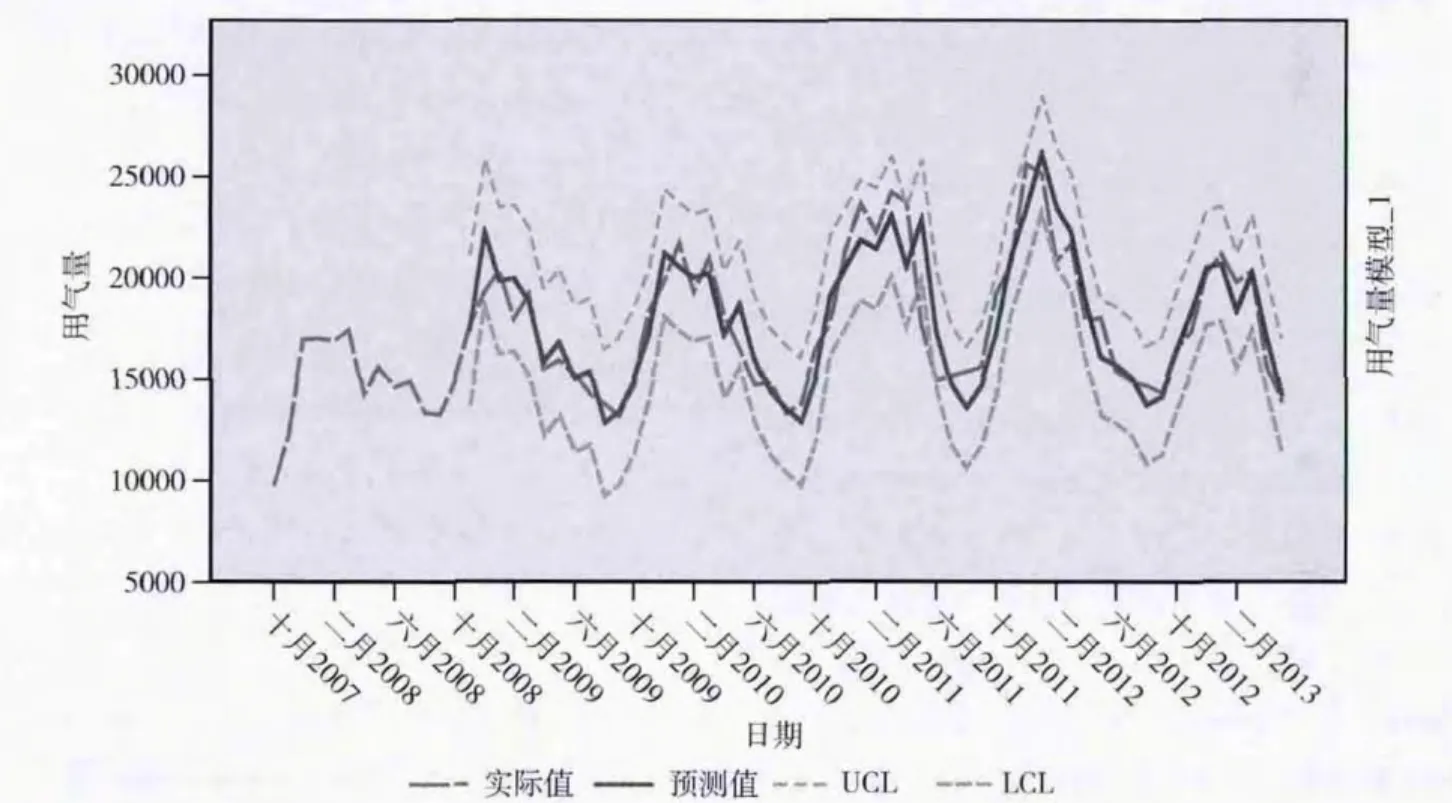
图9 SARIMA（1，1，0）× （0，1，1）模型预测

表2 4种模型的预测准确率／%

3 结束语

本文的工作结果表明：一方面，用SARIMA 模型对片区居民用户液化气使用情况建模，预测片区储气量是可行的，相对其它模型也具有更高的准确率；另一方面，对企业来说，片区储气量的准确预测，可以指导企业减少储气量，节约成本，提高资金周转率，规避由于价格变动带来的资金风险。

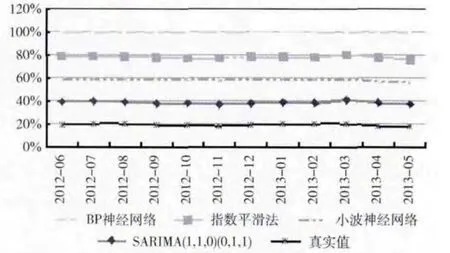
图10 各模型比较

必须注意：由于历史用气数据不全、存在不一致现象；并且每一个月的数据也并非完全真实，而是通过拆分和合并获得，拆分只是简单的按照平均分摊原则，未考虑月份之间的权值差异，尽管这是因为业务上不能满足要求而进行的必要 “暴力”分拆，但是如果我们能够在数据完整性和准确性上有所提高，模型可能会有更好的效果。

考虑到各个用户之间用气多少相互独立，而对用户来说，每个月用气又是重复事件，因而，下一步我们将尝试针对个人用户的用气行为进行聚类［15］，形成虚拟片区，然后再对虚拟片区用气量建模和预测，进而开展保守代扣款业务，以降低企业经营风险和资金周转。

［1］Hamilton J D.Understanding crude oil prices ［R］.National Bureau of Economic Research，2008.

［2］LIU Dongning，TANG Yong，TENG Shaohua，et al.A minimal substructural logic in temporal database［J］.Chinese Journal of Computers，2013，36 （8）：1592－1601 （in Chinese）.［刘冬宁，汤庸，滕少华，等.基于时态数据库的极小子结构逻辑系统 ［J］.计算机学报，2013，36 （8）：1592－1601.］

［3］Dubeau F，Mir Y.Exponential growth model：From horizontal to linear asymptote［J］.Communications in Statistics－Simulation and Computation，2014，43 （10）：2186－2204.

［4］Box G E P，Jenkins G M，Reinsel G C.Time series analysis：forecasting and control ［M］.John Wiley ＆ Sons，2013：374－377.

［5］WANG Lingjian，TENG Shaohua.Application of clustering and time－based sequence analysis in intrusion detection ［J］.Journal of Computer Applications，2010，30 （3）：699－701 （in Chinese）.［王令剑，滕少华.聚类和时间序列分析在入侵检测中的应用 ［J］.计算机应用，2010，30 （3）：699－701.］

［6］Mombeni H A，Rezaei S，Nadarajah S，et al.Estimation of water demand in Iran based on SARIMA models［J］.Environmental Modeling ＆Assessment，2013，18 （5）：559－565.

［7］Paoli C，Voyant C，Muselli M，et al.Forecasting of preprocessed daily solar radiation time series using neural networks［J］.Solar Energy，2010，84 （12）：2146－2160.

［8］Khashei M，Bijari M.A novel hybridization of artificial neural networks and ARIMA models for time series forecasting ［J］.Applied Soft Computing，2011，11 （2）：2664－2675.

［9］Martinez Alvarez F，Troncoso A，Riquelme J C，et al.Energy time series forecasting based on pattern sequence similarity［J］.IEEE Transactions on Knowledge and Data Engineering，2011，23 （8）：1230－1243.

［10］Qasim M，Kanjiya P，Khadkikar V.Artificial neural network based phase locking scheme for active power filters［J］.IEEE Transactions on Industrial Electronics，2014，61 （8）：3857－3866.

［11］Wang J Z，Wang J J，Zhang Z G，et al.Forecasting stock indices with back propagation neural network ［J］.Expert Systems with Applications，2011，38 （11）：14346－14355.

［12］Cao J，Lin Z，Huang G.Composite function wavelet neural networks with extreme learning machine ［J］.Neurocomputing，2010，73 （7）：1405－1416.

［13］Davis J J，Clark A J.Data preprocessing for anomaly based network intrusion detection：A review ［J］.Computers ＆Security，2011，30 （6）：353－375.

［14］LI Aichun，TENG shaohua.Application of web mining technology to click fraud detection ［J］.Computer Engineering and Design，2012，33 （3）：957－962 （in Chinese）. ［李 爱春，滕少华.Web 挖掘在网络广告点击欺诈检测中的应用［J］.计算机工程与设计，2012，33 （3）：957－962.］

［15］Cao H，Li X，Woon Y，et al.Integrated over sampling for imbalanced time series classification ［J］.IEEE Transactions on Knowledge and Data Engineering，2013，25 （12）：2809－2822.