基于Chwa ＆Hakimi模型的GA－BPFD算法

宣恒农，刘田田，张润驰

（南京财经大学 信息工程学院，江苏 南京210046）

0 引 言

对系统级故障诊断的研究是建立在故障模型基础之上的［1－5］，主要模型有测试模型和比较模型两类。系统故障诊断算法发展至今，研究成果颇丰。张大方等提出了集团诊断算法，结合图论的相关知识确定系统中的故障节点；笔者等建立了基于方程的诊断理论，根据测试结果矩阵直接求取绝对故障基方程诊断算法的最大特点是对系统中的故障节点数目无任何要求，不需要满足t－可诊断性［6］。近年来，由于群体智能算法具有自学习、自组织、自适应的特征和实现简单、鲁棒性强等优点，运用群体智能方法解决系统级故障诊断问题渐渐成为主流［7，8］。

1 相关研究

Elhadef等运用遗传算法 （genetic algorithm，GA）解决了PMC模型下的系统级故障诊断问题，李炯城等改进了遗传算法并取得良好的效果［9］；Mourad Elhadef等首次将BP神经网络应用到Chwa ＆ Hakimi模型下的系统级故障诊断问题，得到了BPFD 智能诊断算法［5］，仿真结果表明，BPFD 算法具有极高的诊断精度。然而由于BP神经网络本身的局限性，初始参数的选择对迭代次数与结果误差的影响很大。本文将探究基于Chwa ＆ Hakimi模型，用遗传算法对BPFD 算法进行了改进，提出了GA－BPFD算法。仿真结果表明，算法在稳定性与时间复杂度方面具有明显的优越性。

根据Chwa ＆ Hakimi模型的定义，对于由n 个节点组成的系统v＝｛v1，v2…，vn｝，让任意一对相邻节点vi、vj（i≠j）执行相同的测试任务，接着对所得结果进行比较。若两个节点的运行结果一致，则这两个节点都认为对方通过了测试，否则，都认为对方未通过测试。根据双方的故障状态可分为3种情况：正常节点与正常节点比较，其结果必为正常；正常节点与故障节点 （或故障节点与正常节点）比较，其结果必为故障；故障节点与故障节点比较，其结果可能为正常，亦可能为故障。令vi＝0表示vi为正常节点，vi＝1表示vi为故障节点，用wij＝0 （或wji＝0）表示vi与vj的运行结果一致，wij＝1 （或wji＝0）表示vi与vj的运行结果不一致。将全部这样的wij以i 为行号、j为列号的规则存储在一个n 阶矩阵W 中，称W 为系统X 的一个测试症候矩阵。

2 GA－BPFD算法的主要过程

对BP神经网络训练的过程就是对其权值和偏置值不断优化改进的过程，初始参数的选择十分关键，不当的初始参数会使算法的解空间搜索范围陷入局部。考虑到遗传算法全局搜索的特点能有效克服BP 神经网络解的局限性问题，我们首先用遗传算法生成BP神经网络的初始参数。

用GA 算法改进BPFD 算法，重点需要考虑以下几个问题：GA 算法初始种群的选取；适应度函数的构造；选择、交叉和变异算子的设计；与BPFD 算法的结合方式等。下面我们对改进算法进行逐一分析。

为叙述方便，对 vi∈V（1≤i≤n）；我们用γ（vi）表示V 中所有与vi相邻的节点构成的集合，即γ（vi）＝｛vj｜vj∈V，（vi，vj）∈E｝；用e（vi）表示V 中所有与vi相接的边构成的集合，即e（vi）＝｛eij｜vj∈V，eij∈E｝。于是不难得到如下结论。

定理1 在Chwa ＆ Hakimi模型下，设故障模式与其症候相容，则：

（1）若eij＝0，则ui－uj＝0；

（2）若eij＝1，则（ui＋uj－1）（ui－uj）＝0。

证明：当故障模式与症候S 相容时，根据Chwa ＆Hakimi模型的定义，若eij＝0，则必有ui＝uj＝0或ui＝uj＝1，于是有ui－uj＝0；若eij＝1，则必有ui＝0，uj＝1，或ui＝1，uj＝0，或ui＝uj＝1。显然，上述3种情况均满足（ui＋uj－1）（ui－uj）＝0。

综上，定理1得证。

2.1 选取初始种群

我们先随机生成GA 算法的初始种群，即BP神经网络的权值和偏置值，种群中个体的编码采用实数编码方式。

2.2 构造适应度函数

GA 算法的核心是适应度函数的设置，设置的好坏直接影响算法的收敛速度和最终解的获得。在本文中，适应度函数fit采用BP神经网络中误差平方和的倒数，即

式中：sol表示种群中的每个个体，种群中的个体数为n。实际输出与期望值之间的差值越小，适应度函数的值就越大。

2.3 设计选择算子

通用的选择操作包括轮盘赌、（μ＋λ）选择和期望值选择等方法。这里采用轮盘赌选择方法：每个个体被选择的概率与其在整个种群中的相对适应度成正比 （因此该法又被称为适应度比例选择法）。具体步骤如下：

步骤1 计算每个个体在轮盘中的选择概率。设种群数目为n；个体适应度为fit（sol），则sol 被选择的概率P（sol）为

显然，个体的适应度越大，被选中的概率也就越高。

步骤2 计算每个个体的累加概率，其中

步骤3 在轮盘中随机选择n 次，其具体的选择方法如下：

（1）产生一个 ［0，1］之间的随机数r；

（2）如果r＜q1，则选择第1个个体，若qi－1＜r≤qi，则选择第i个个体。

通过上述方法，适应度高的个体会被尽可能地保存至下一代。

2.4 设计交叉算子

由于采用实数编码的方式，因此采用简单交叉的方法。根据交叉概率pc，从种群P1中选择pc＊t个个体与种群P1中的个体进行单点交叉。具体步骤如下：

步骤1 比较两个个体的基因不同的位；

步骤2 列出基因不同位基因的所有组合，选出其中满足t－可诊断性的个体，并按适应度值由高到低的顺序排列；

步骤3 选出适应度最高的两个个体作为杂交后的最终个体。

2.5 设计变异算子

变异的操作很大程度上依赖于变异概率pm，根据变异率pm选择变异个体，当适应度函数值小于变异概率时，进行基因翻转操作。

2.6 GA算法与BPFD算法的结合

步骤1 通过以上步骤将得到误差最小的一组神经网络权值和偏置值，并以此作为神经网络的初始权值；

步骤2 通过前向计算、误差的计算、反向传播和权值更新等操作进行神经网络的训练；

步骤3 判断是否满足精度要求，若达到要求即输出结果，否则再次进行训练。

由于经过了遗传算法的全局搜索，所以再次陷入局部极小值的可能性不大。

3 GA－BPFD算法的步骤与效率分析

在上述步骤的基础上，我们将GA－BPFD 算法的完整过程总结如下：

输入：测试报告

输出：故障集F，无故障集FF

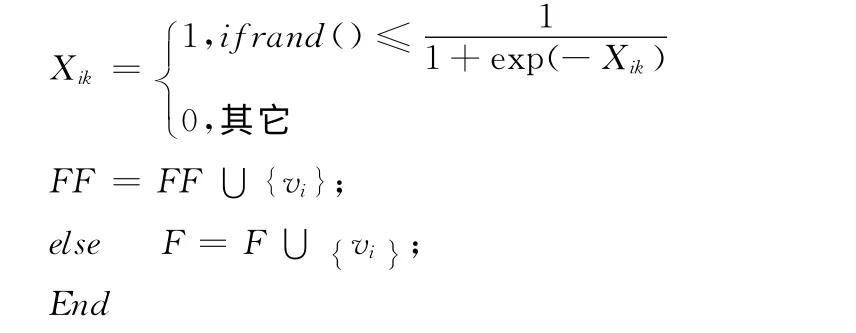
算法流程如图1所示，上述的6 个步骤顺序执行，我们逐步分析算法的时间复杂度。第一步，初始化随机生成初始种群P0，种群大小为n，时间复杂度为Ο（n）；第二步，计算每个个体的适应度，遍历整个种群，种群大小为n，时间复杂度为Ο（n）；第三步，采用轮盘赌法进行选择，计算个体的适应度总和时复杂度为Ο（n），选择过程中共进行了n次，所以时间复杂度为Ο（n）；第四步，交叉过程中采用的是单点交叉，最坏的情况是所有的个体均参与了交叉，时间复杂度为O（n2），最好的情况是无种群个体参与交叉，时间复杂度为O（1）；第五步，最坏情况下，所有种群个体均发生了变异，时间复杂度为O（n2），最好情况下，没有个体发生变异，时间复杂度为O（1）；第六步，神经网络训练，时间复杂度为O（n2）。

图1 GA－BPFD算法流程

因此，算法总的时间复杂度为Ο（n）＋Ο（n）＋Ο（n）＋Ο（n）＋Ο（n2）＋Ο（n2）＋Ο（n2）＝O（n2），即在最坏情况下，时间复杂度均为O（n2）。BPFD 算法为了避免得到的是局部最优解，增加了相应的额外步骤，算法的时间复杂度为Ο（n3）。相较之下，GA－BPFD 算法有效地降低了诊断的时间复杂度。

4 实验仿真

我们对GA－BPFD算法与BPFD 算法进行了仿真比较。仿真均在一台配置为Core（TM）2 2.33GHz CPU，2.00 G 内 存 的 计 算 机 上 用Matlab 语 言 编 程 实 现［10－12］。根 据Chwa ＆ Hakimi模型，我们首先随机生成不同规模的网络拓扑连接图与符合t－可诊断性的故障模式，通过模拟测试，得出测试报告，以此作为算法的输入。

当种群大小设置为50，迭代次数设置为100、200时，由本文提出的方法进行遗传迭代得到误差平方和变化曲线图，如图2 （a）、（b）、（c）所示，从图2中我们可以看到，由100－200代，误差平方和下降基本趋于一个稳定最小值，在训练过程中误差趋于最小，这说明了改进算法分析实现的合理性。而适应值在50－60代内趋于稳定并得到最优的初始权值，这将作为BPFD 算法训练的初始权值。

图3展示了当系统节点数为200 时，两个算法的均方根误差、诊断时间和故障单元数的综合比较。根据系统的t－可诊断性，故障节点的数目从1 递增到99。图4 展示了随着系统规模的增加，两种算法在CPU 运行时间方面的比较，更加凸显了改进后的算法的优越性。

结合大量实验的结果，我们得出以下结论：

对于诊断误差，如图3所示，GA－BPFD 算法的诊断误差较小，在准确性上要优于BPFD 算法；在诊断的稳定性方面，BPFD 算法的稳定性较差，而GA－BPFD 算法诊断结果则趋于稳定；在算法的泛化性能上，由于BP网络的性能评价函数值与误差呈负相关，改进后的GA－BPFD 算法的输出误差较改进前有了极大降低。而随着故障节点数的增加，算法诊断的误差并没有随之增大，在保证算法训练精度的同时，网络的泛化精度也能得到满意值；在诊断时间方面，如图4 所示，随着系统规模节点数的不断增大，BPFD 与GA－BPFD 算法所用时间也相应增加。但GABPFD 算法所用时间明显少于BPFD 算法所用时间，随着系统规模的增大，尤其实在节点数目大于100 以后，GABPFD 算法的时间效率要明显高于BPFD 算法。

5 结束语

图2 GA 的预处理

本文提出了GA－BPFD算法。与BPFD 算法相比，GABPFD 算法由于预先以GA 算法进行参数预处理，得到了一个较为优越的初始权值与偏置值，大幅降低了算法在BP神经网络迭代学习过程中非必要的迭代运算，使得算法在进行故障诊断时收敛速度加快，总体的时间复杂度降低；同时对BP神经网络泛化能力的分析可知，在训练过程中算法对不同样本值也能给出准确的诊断。

对于BP神经网络泛化性能的研究，目前还处在初级阶段。通过对神经网络本身性质的研究来改进算法性能，将会是进一步的研究方向。同时，其它智能算法，如模拟退火等对BPFD 算法改进的研究还有待进一步探讨。

实际上，GA－BPFD算法不仅仅适用于Chwa ＆Hakimi模型，对于PMC 模型、BGM 模型和Malek模型，只要根据各模型的特征，将算法进行相应调整，亦可适用。因篇幅所限，我们将另文专述。

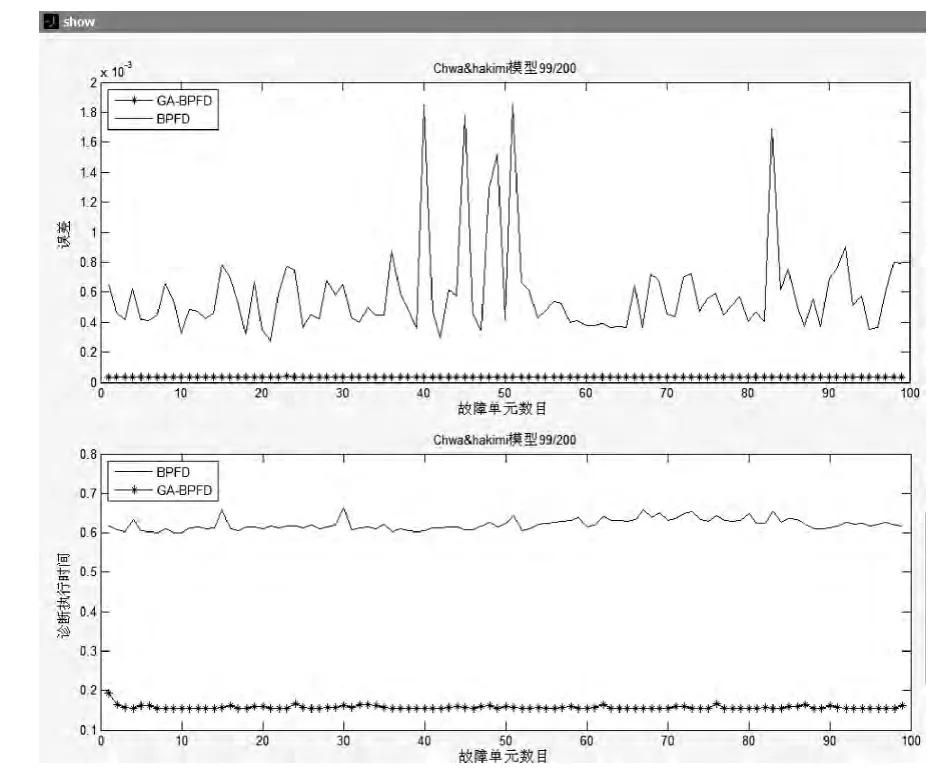
图3 系统规模为200时误差和时间比较

图4 CPU 时间随节点增加的变化

［1］Wu X，Zhu X，Wu GQ，et al.Data mining with big data［J］.IEEE Transactions on Knowledge and Data Engineering，2014，26 （1）：97－107.

［2］Ui－Min Choi，Kyo－Beum Lee，Blaabjerg F.Diagnosis and tolerant strategy of an open－switch fault for t－type three－level inverter systems［J］.IEEE Transactions on Industry Applications，2014，50 （1）：495－508.

［3］Mourad Elhadef.Solving the PMC－based system－level fault diagnosis problem using hopfield neural networks ［J］.IEEE International Conference on Advanced Information Networking and Applications，2011：216－223.

［4］Mourad Elhadef.A modified hopfield neural network for diagnosing comparison－based multiprocessor systems using partial syndromes［J］.IEEE 17th International Conference on Parallel and Distributed Systems，2011：646－653.

［5］Mourad Elhadef，Amiya Nayak.Comparison－based systemlevel fault diagnosis：A neural network approach ［J］.IEEE Transactions on Parallel and Distributed Systems，2012，23（6）：1047－1059.

［6］XUAN Hengnong，HE Tao，XU Hong，et al.Two points diagnostic algorithm based on Chwa ＆Hakimi fault model［J］.Computer Engineering and Applications，2010，46 （5）：66－68（in Chinese）. ［宣恒农，何涛，许宏，等.基于Chwa ＆Hakimi故障模型的二分诊断算法 ［J］.计算机工程与应用，2010，46 （5）：66－68.］

［7］Arora S，Singh S.The firefly optimization algorithm：Convergence analysis and parameter selection ［J］.International Journal of Computer Applications，2013，69 （3）：48－52.

［8］Yang XS，He X.Firefly algorithm：recent advances and applications ［J］.International Journal of Swarm Intelligence，2013，1 （1）：36－50.

［9］LI Jiongcheng，WANG Yangyang，LI Guiyu，et al.Rapid convergence of hybrid genetic algorithm ［J］.Computer Engineering and Design，2014，35 （2）：686－689 （in Chinese）.［李炯城，王阳洋，李桂愉，等.快速收敛的混合遗传算法［J］.计算机工程与设计，2014，35 （2）：686－689.］

［10］Wan Weishui，Shingo Mabu，Kaoru Shimada，et al.Enhancing the generalization ability of neural networks through controlling the hidden layers ［J］.Applied Soft Computing，2009，9 （1）：404－414.

［11］ZHU Kai.Proficient in MATLAB neural network ［M］.Beijing：Electronic Industry Press，2010 （in Chinese）. ［朱凯.精通 MATLAB 神 经 网 络 ［M］.北 京：电 子 工 业 出 版社，2010.］

［12］Nakama T.Theoretical analysis of batch and on－line training for gradient descent learning in neural networks ［J］.Neural Computing，2009，73 （1－3）：151－159.