软件接收机中QPSK 信号同步器的设计与实现

马 涛，雷洪利，向 新，王 锋，孙 晔

（空军工程大学 航空航天工程学院，陕西 西安710038）

0 引 言

传统的QPSK 信号接收机需要对接收信号首先进行载波同步，然后进行位同步，由于在位同步过程中过采样策略能有效提高同步性能，因此需要系统工作在比较高的采样率下，这无疑会占用大量的系统资源。

本文针对QPSK 信号的特点，考虑到软件接收机的工作机制，使用了一种首先利用Gardner定时恢复算法［1］进行位同步，然后再利用Costas环载波相位补偿算法对信号进行载波同步的工作方式。根据数字锁相环的相关理论对这种工作方式的可行性、工作过程、资源利用、参数设置和系统性能进行了分析和仿真。研究结果表明，这种工作方式能有效降低同步器的复杂度，使同步器工作在比较低的采样率下；仿真结果表明，同步器收敛速度快，对系统误码率的影响比较小。为同步器的实际应用提供了依据。

1 定时恢复原理

位同步也称为定时恢复，其目的是实现码元采样相位的最佳化，即让抽样脉冲在最佳位置进行抽样，由于在初始阶段无法确定最佳相位，因此需要通过锁相环路反馈调整和误差检测算法来实现上述目标。

定时恢复环路的实现结构如图1所示，由插值滤波器、定时误差检测器、环路滤波器和NCO （控制器）组成。x（t）是接收信号经下变频和匹配滤波器后输出的基带信号，通过频率为1／Ts的本地时钟 （T／Ts很可能是一个无理数）对x（t）进行过采样后得到x（m），插值滤波器对x（m）进行插值和重采样，重采样频率为1／Ti，此时每个符号有k＝2个采样点，得到y（k），利用Gardner算法从y（k）中提取定时误差，定时误差经环路滤波器后控制NCO，使NCO产生插值滤波器需要的参数mk和μk，完成定时恢复。

图1 位同步器结构

1.1 插值滤波器

插值滤波器的主要功能就是对接收的过采样序列进行滤波和重采样，并且从重采样序列中获得最佳采样值。

设经1／Ts采样后的信号［2］为

式中：ci——基带码元，Δθ——下变频后的相位偏差，h（t）——余弦滚降滤波器，τ——接收延时，n（kTs）——采样后的噪声信号。

插值滤波器对x（mTs）进行重采样，每个码元采两个样点，环路收敛时，其中一个样点为最佳采样点，其输出为

为了简化计算，对式 （2）重新整理可得

式中：mk——kTi／Ts的整数部分，令int［］表示向下取整，就有mk＝int［kTi／Ts］。μk——kTi／Ts的 小 数 部 分，有μk＝kTi／Ts－mk。同时可以得到i＝int［kTi／Ts］－m。

通过式 （3）可知，哪些采样点需要参与运算由mk决定，而滤波器的冲激响应则由μk 决定。由于插值滤波器仅需得到插值，即重采样值，因此仅需获得插值的频率和相位即可，其冲激响应不必求得。所以可以使用Farrow 结构［3］实现插值滤波器。Farrow 结构能有效降低计算的复杂性，用移位替代乘法运算。本文采用α＝0.5的分段抛物线插值滤波器。

为了实现Farrow 结构的滤波器，令

将式 （4）代入式 （3）可得

系数bl（i）是独立于μk 的固定值，可以直接通过查表获得。

1.2 定时误差检测

根据式 （1），定时恢复时存在载波相位偏差，因此定时误差检测采用对载波相位不敏感的Gardner算法，其计算公式为

式中：y（tn）和y（tn－1）——当前码元和前一码元的最佳采样值，y＊（tn－1／2）——两个码元的中间值，其大小反映了误差的大小。由式 （6）可知，使用Gardner算法提取定时误差，每个符号仅需要两个采样点，每个符号周期只需要计算一次定时误差，因此十分适合硬件实现。

为了减小噪声对定时误差的影响，可以对y（tn）和y（tn－1）进行归一化，仅保留其符号信息，其计算公式为

改进后的Gardner算法仍然具有对载波相位不敏感的特性。同时在相邻码元相同时输出为零，对环路不做出调整。

1.3 环路滤波器

在定时恢复环路中，环路滤波器决定了环路的捕获和跟踪性能，同时能减小噪声对环路稳定的影响。本文采用锁相环中常用的比例积分滤波器［4］，其结构如图2所示。

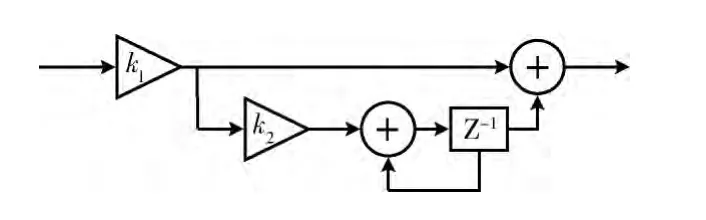
图2 环路滤波器结构

定时恢复环路相当于一个二阶二类的数字锁相环。为了计算k1和k2的值，令k＝kpkvk1，其中，kp为误差检测灵敏度，反映定时误差检测算法的性能［5］，在PSK 调制系统中，针对Gardner算法，kp的值可由式 （8）计算得到，其中α为滚降系数。kv是控制器增益，取kv＝1

当k2＜k＜0.2时，等效噪声带宽由式 （9）定义在满足系统带宽与采样率之比足够小时，有如下定义

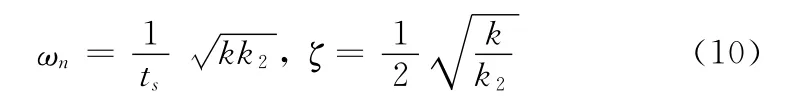
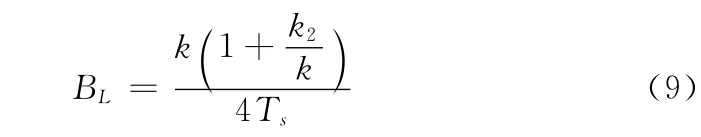
式中：ωn和ζ——模拟锁相环中的无阻尼固有频率和阻尼系数。ζ 一般取0.707，因此可以得到k2＝k／2，代入式（9）中，可得

通过式 （11）即可确定环路滤波器的系数，BLTs的取值需要根据实际情况确定。

1.4 控制器

控制器 （NCO）的作用主要是根据接收的误差信号为插值滤波器提供基点索引mk和小数间隔μk 的值。其原理相当于对一个固定的控制字以及误差信号进行累加，在累加器的溢出时刻输出采样脉冲以及小数间隔μk 的值。

由于插值滤波器内部存在延时单元，因此mk的值不需要计算出来，只要在NCO 的溢出时刻根据寄存器中当前的几个信号值计算出插值，即通过NCO 得到插值频率和相位。

根据NCO 累加器的值η（m）以及控制字W（m） （W（m）中包含环路滤波器输出的误差），可以得到归一化的相位累加器的值［6］

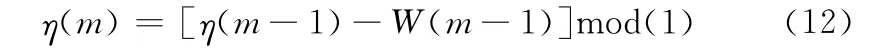
为了便于计算，式 （12）是一个递减型NCO 的表达式。在环路收敛的条件下，W（m）接近常数，此时有W（m）＝Ts／Ti。小数间隔μk 的值就可以利用NCO 累加器计算出来。令ε0＝1／W（m），有μk＝ε0η（m）。

2 载波相位补偿原理

载波相位补偿即载波同步，但载波相位补偿环路之前接收信号已经进行下变频处理，因此载波同步仅需要做相位的估计，不需要对接收信号的频率进行跟踪。由于下变频过程中并没有使用一个完全相干的载波，因此下变频后的信号中存在着残留的频差和相差，并且伴随着信号从定时恢复环路输出，叠加在最佳判决值上。

定时环路中，信号经过插值滤波器后每个码元仅有两个样点，对NCO 输出频率进行分频，就可以获得最佳判决时刻，即通过插值滤波器输出得到最佳判决点。因此，只要估计出下变频时的载波相位误差即可得到最佳判决值。

2.1 开环结构下的载波相位补偿

当下变频频率与载波频率一致时，可以采用一种开环结构的载波相位补偿方式，也称为前馈的补偿方式。其实现结构［7］如图3所示。

图3 开环结构载波相位补偿原理

根据式 （1），设ci＝ai＋jbi，定时恢复完成后，由于每个码元仅含有一个最佳判决点，在不考虑噪声的情况下，设相差为Δθ，信号可以简单记作 （省略样点间隔2Ti）

将式 （13）写作I路和Q 路两路信号，即

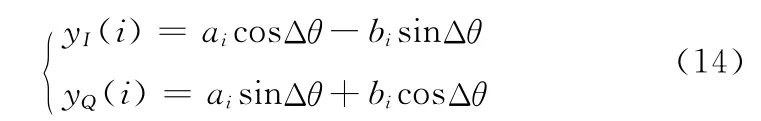
对yI（i）和yQ（i）分别进行归一化，仅保留其符号值，记作sgn ［yI（i）］和sgn ［yQ（i）］，相位误差θ（i）［8］可通过式 （15）计算获得

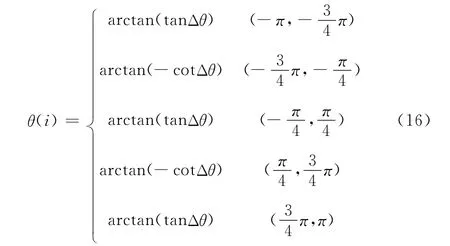
因此同步后基带码元可以通过式 （17）得到

将式 （16）化简代入式 （17）中，可以得到载波相差与解调出的基带码元的关系如式 （18）所示

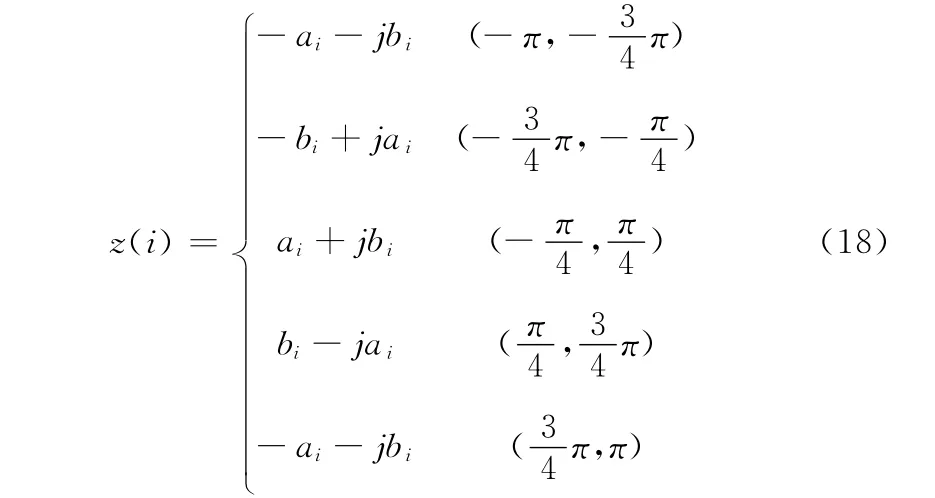
开环结构的原理和实现过程都比较简单，并且不需要收敛时间。但是开环结构没有反馈，因此对相位也没有跟踪，当下变频频率与载波频率有偏差时，相位误差也会循环增长，一旦相差落入不同的两个区间时，I、Q 两路信号就会出现如式 （18）所示的相位模糊情况，并且循环往复，导致得到一组基带码元并非原始的基带码元。而且，在存在噪声的情况下，这种不同区间的跳变会变得更加没有规律。因此，只有在通信时间较短，下变频与载波频率相干性较好，并且信噪比足够高的情况下这种开环结构才能够被使用。显然，实际的通信系统很难满足这样苛刻的条件。

2.2 闭环结构下的载波相位补偿

在开环结构下，当下变频频率和载波频率有误差时，相位误差会在0－2π区间内跳变，因此解调出的信号是不可用的。为了克服这个问题，通常情况下使用闭环形式的载波相位补偿方式，即反馈的锁相环方式。其实现结构与位同步环路类似，如图4所示。

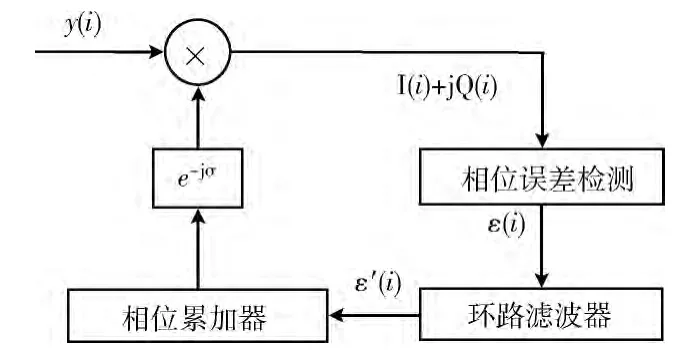
图4 闭环结构载波相位补偿原理

2.2.1 相位误差检测器

相位误差检测器的结构与图3类似。

参照2.1节中的变量定义，设环路输出的相位补偿值为e－jσ，与y （i）相乘可得

当Δθ－σ≈0 时，I（i）和Q（i）分别就是需要的两路码元。

对比式 （19）与式 （14），其结构是类似的，因此可以对式 （19）进行与式 （14）相同的处理。设相位误差检测器输出为ε（i），则可以得到闭环结构下ε（i）与Δθ－σ的关系等同于式 （16）中θ（i）与Δθ 间的关系。但式 （14）中Δθ是下变频的相位误差，而式 （19）中Δθ－σ则是下变频的相位误差与环路产生的估计相位的差。

因此，根据下变频初始相位误差的不同，通过相位误差检测器可以得到一个和式 （18）相近的结论 （相差为Δθ－σ，解调得到的码元为I（i）＋jQ（i））。由于软件接收机中下变频在模拟端完成，相位误差依然有可能会落入各个区间内，但是此时环路能够收敛，即相位误差会直接收敛在任何一个区间内，而不会在各个区间之间跳变。因此可以插入一段固定的码元序列，然后对码元序列的识别来判断初始相位的区间。

2.2.2 环路滤波器

环路滤波器与定时恢复环路中环路滤波器结构相同，即采用比例积分滤波器。其作用与参数计算可参考1.3节。载波相位补偿环路中有kp＝1，kv＝1。

2.2.3 相位累加器

相位累加器的功能就是对相位误差检测输出的相位误差进行累加 （mod （2π）），其结构与定时环路中NCO 中的相位累加器相似，但没有固定的控制字。这是由于接收信号已经进行下变频，相位累加器只需要提供相位估计，不需要输出特定的频率。即由于提前对信号进行了下变频处理，因此环路中NCO 就退化成了相位累加器。

3 仿真及性能分析

3.1 仿真模型及参数

本文在Matlab／Simulink 环境［10］下对该同步器进行设计和仿真，模型主要参数为：码元速率设定为1 Mbps，接收端过采样速率为8 Mbps，发送和接收端采用滚降系数为0.5的根升余弦滤波器作成形滤波。采用QPSK 数字调制方式。其实现流程如图5所示。

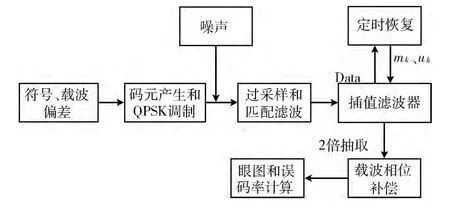
图5 模型仿真流程

3.2 性能分析

本文将分别在无噪条件下及高斯噪声条件下对同步器系统性能进行分析。在无噪条件下，观察系统各部分控制信号的波形，以及测试环路的收敛速度，保证理想条件下同步器系统的可行性；在高斯噪声条件下，测量系统的误码率，并与实际接收机进行比较，分析在高斯环境下的系统性能。

3.2.1 等效噪声带宽的选取

由于环路滤波器的等效噪声带宽对系统性能具有比较大的影响，其值越大环路收敛越快，但定时和相位补偿的偏差也越大，甚至会出现码元丢失或者载波相位落入不同区间的情况，使同步得到的基带码元失去了意义。相反，其值越小环路收敛越慢，当系统存在较大频差时，过小的带宽值会使环路的捕获性能变得极差。但等效噪声带宽的选择上并没有明确的定义，需要根据实际情况确定。为了仿真能兼顾收敛速度以及可靠性，经过多次对比实验，最终将定时恢复环路中环路滤波器等效噪声带宽设为0.002，相位补偿环路中环路滤波器等效噪声带宽设为0.02，以下分析都将基于此设定。

3.2.2 无噪条件下的同步器性能

为了更直观地观察同步的工作过程，首先假定噪声为零，设码元频差为0.25、载波频差为0.025。通过Matlab／Simulink环境下的scope模块分别观察定时环路误差控制信号w（n），小数间隔μk，相位补偿环路控制信号ε’（i），相位估计ζ（i）的仿真仿真曲线，由此可以看到定时恢复环路和载波相位补偿环路的收敛情况，如图6所示。

通过对系统进一步分析，在无噪条件下，可以观察到环路收敛时间随码元频差的增加而增长，当码元频差小于1%，载波频差为0时，环路在10－3s内即可达到收敛。

而当码元频差固定为0.5%，同理可以观察到环路收敛时间虽载波频差的增加而增长，但载波频差小于0.075%时，收敛时间都接近于10－3s，这是由于在相位补偿环路中，环路滤波器中的累加器在定时恢复过程中已经有了一个接近于可以跟踪载波频差的值，因此定时恢复完成后，相位补偿也能很快完成。而当频差继续增大时，收敛时间则增长较快。

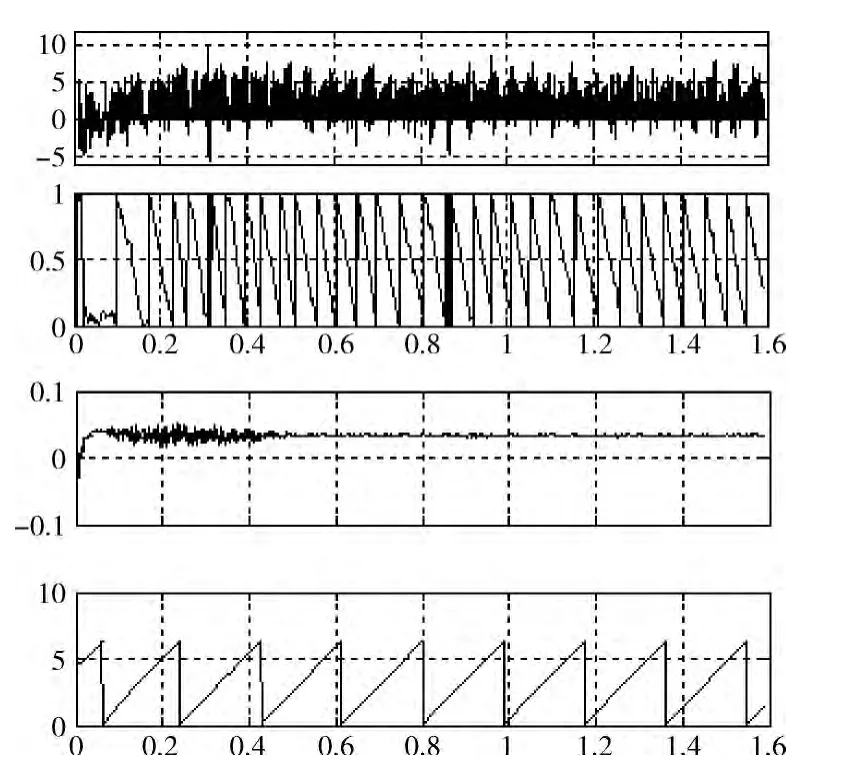
图6 仿真波形

3.2.3 高斯环境下的同步器性能

当系统加入高斯噪声后，仿真表明，环路收敛需要要的时间会大大增加。例如，在载波频差为0.075%的情况下，无噪条件下环路收敛所需要的时间小于10－3s，而当信噪比为7dB时，实际环路收敛所需要的时间为3000×10－6s，相比无噪声条件下增加了2倍。

码元频差取码元速率的0.5%，载波频差取载波频率的0.05%时，误码率［11］分析如图7所示。

图7 系统误码率仿真

由图7可知，同步环路的性能良好，通过定时恢复和相位补偿，能够完成同步，取得最佳判决值。环路的抗噪声性能良好，因此与实际接收机的误码率特性曲线十分接近。

4 结束语

本文通过对Gardner算法和Costas环载波同步算法进行分析和研究，提出了一种QPSK 信号同步器，给出了同步器各部分的参数设定。该同步器能够工作在比较低的采样率下，适合应用于软件接收机中，并且对码元频偏和载波频偏有一定的跟踪能力。仿真结果表明，同步器能够跟踪1%以上的码元频差和0.1%以上的载波频偏。同步系统在码元速率为1Mbps时，基本能在10－2s内完成收敛，同步环路对系统误码率影响较小，性能良好。

［1］Chen Qin，Li Min.Modified Gardner algorithm for bit synchronization in high－order QAM system ［C］／／IEEE Conference Publications，2013：428－429.

［2］Silva C，Eric M，Gordana JD.Design and simulation of QPSK reconfigurable digital receiver ［C］／／53rd IEEE International Midwest Symposium on Circuits and Systems，2010：656－659.

［3］Valentin V，Vladimir P，Pavel P.DSP source code optimization of BPSK／QPSK receiver symbol synchronization recovery circuit［J］.International Conference on Electronic Devices，Systems and Applications，2011：208－212.

［4］Juan AM，Nicolas AC，Pedro AR，et al.A high data rate BPSK receiver implementation in FPGA for high dynamics applications ［C］／／VII Southern Conference on Programmable Logic，2011：233－238.

［5］FU Yongming，ZHU Jiang，JU Yingyu.Parameters design and performance analysis of the timing recovery loop based on Gardner timing detector ［J］.Journal on Communications，2012，33 （6）：191－198 （in Chinese）.［付永明，朱江，琚瑛珏.Gardner定时同步环路参数设计及性能分析 ［J］.通信学报，2012，33 （6）：191－198.］

［6］Zhang Lili，He Zhiming.A modified timing synchronization algorithm for QPSK in digital receiver ［C］／／2nd International Conference on Artificial Intelligence，Management Science and Electronic Commerce，2011：1821－1824.

［7］Wilfried G.Open－loop analysis of a nonlinearly modified Gardner synchronizer ［J］.Browse Journals ＆ Magazines，2014，18 （11）：1963－1966.

［8］Maarten T，Michiel S，Patrick R.Time domain model for costas loop based QPSK receiver［C］／／8th Conference on Ph.D.Research in Microelectronics and Electronics，2012：313－316.

［9］Shi Dengsheng，Yan Chaoxing，Wu Nan，et al.An improved symbol timing error detector for QPSK signals ［C］／／6th International ICST Conference on Communications and Networking in China，2011：1088－1092.

［10］ZHANG Shuiying，XU Weiqiang.Principles and Matlab／Simulink simulations of commuications ［M］.Beijing：Posts＆Telecom Press，2012：242－253 （in Chinese）. ［张水英，徐伟强.通信原理及Matlab／Simulink仿真 ［M］.北京：人民邮电出版社，2012：242－253.］

［11］Proakis JG，Salehi M.Digital communication ［M］.5th ed.Beijing：Publishing House of Electronics Industry，2009：114－127.