基于单双亲混合GA的复杂拣选作业优化

李 晓，项 前＋，吕志军，管树林（.东华大学 机械工程学院，上海060；.上海精星仓储设备工程有限公司，上海06）

0 引 言

对于拣货作业优化问题的研究，曾经有学者利用启发式算法［1］研究订单分批策略，在此基础上对拣选路径进行优化；也有学者把拣选作业优化问题抽象成旅行商 （TSP）问 题，分 别 利 用 遗 传 算 法［2，3］、蚁 群 算 法［4，5］、多 种 群 果 蝇算法［6］、启发式TSP算法［7］、MMAS算法［8］等对此问题进行过研究，且取得了不错的效果。然而以上研究方法简化了问题的复杂性，忽略了装箱约束条件，王占磊［9］、周超［10］等在考虑了装箱约束条件的前提下，对单一作业拣选优化问题进行了研究；由于配送中心很多时候同时进行多个出入库作业，周军等［11］在兼顾最小路径原则和先进先出原则的基础上，对复合作业拣选路径优化进行了研究。以上都取得了可喜的研究成果，但忽略了多品项拣选时复杂约束条件。据此，本文在考虑多品项约束的前提下，建立储存区复杂拣选作业优化模型，基于一种单双亲混合GA对作业顺序和储位分配同时进行优化求解，以达到缩短拣选路径、提高拣选效率的目标。

1 复杂拣选作业优化模型

1.1 模型描述与假设

（1）储存区布局：如图1所示，出入库台位于货架的同侧，每条拣货巷道都设有一台堆垛机。一个储物单元包括：两排货架、一条拣货通道、一台堆垛机；本文仅对单个仓储单元的拣选作业进行优化求解；

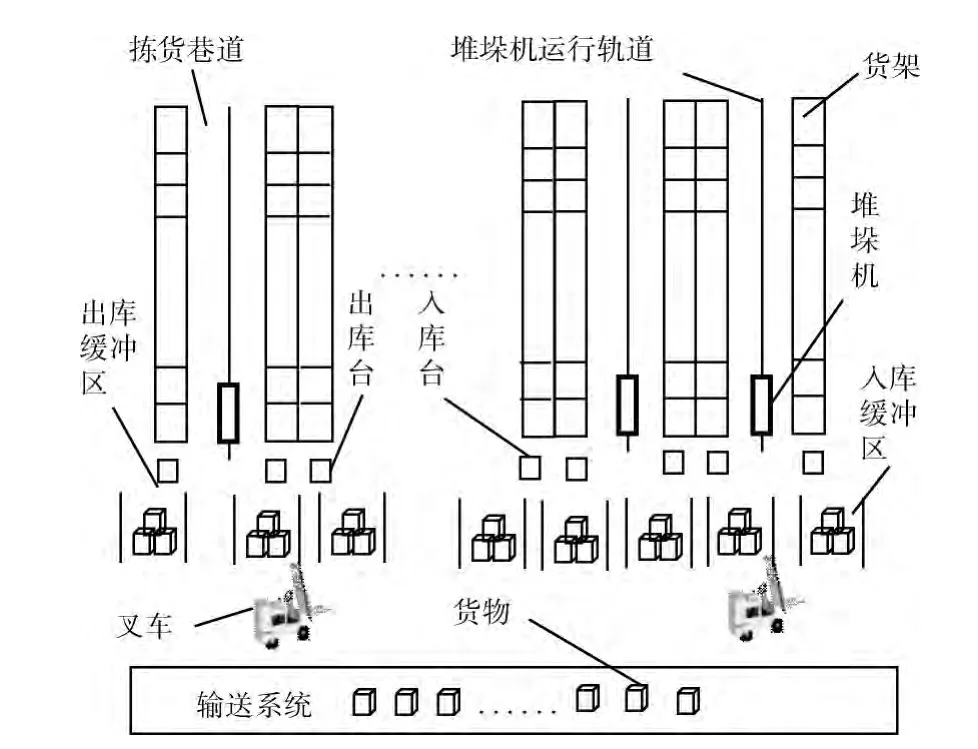
图1 储存区布局

（2）拣选作业工作流程：堆垛机接收到仓储控制系统（WCS）发送的出入库任务序列后，从出入库台出发，首先运行至第一作业任务的目标储位，对其进行存取操作；然后执行下一个作业任务，直至所有的作业任务完成，若改变任务序列的顺序，将有不同的拣选路径与之对应；

（3）每个储位只能存放一个货物单元 （托盘或集装箱）［12］，且货架上的品项储存类型和存放状态 （有物料／无物料）已知，因此求解过程中可及时查询获得各品项的出入库约束域；

（4）堆垛机的每次存取操作对象为单个品项的一个货物单元，堆垛机对每个操作品项的存、取动作所用时间相等；

（5）堆垛机匀速运行，故可用堆垛机运行路径来衡量堆垛机的存取效率；当堆垛机执行完最后一个任务后返回到出入库台。

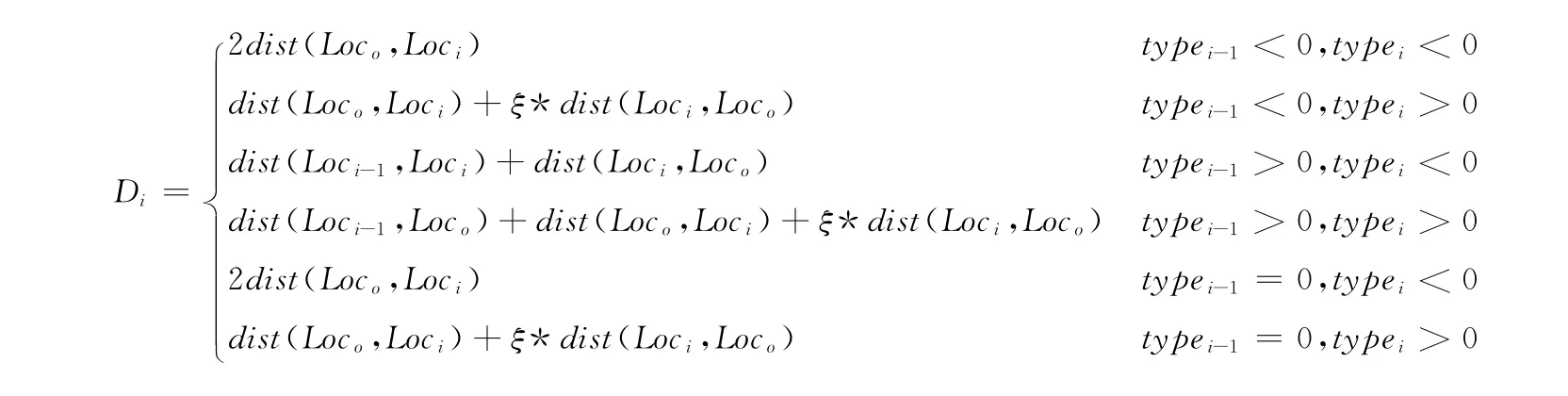
1.2 复杂拣选作业数学模型

1.2.1 模型相关符号描述

（1）MRxC：单排货架储存矩阵，R 表示货架层数，C表示货架列数。MRxC第i 层第j 列的元素Mij∈Z（整数集），表示品项编码号，Mij＞0时表示该储位有物料存储，Mij＜0时表示该储位无物料；

（2）T：初始任务矩阵，T＝ （T1，T2，…，Tn），n∈Z＊（正整数集），代表任务的个数。其中Ti＝（typei，toi）T，typei表示任务类型，typei∈Z（整数集），表示品项编码号，typei＞0时表示入库任务，typei＜0时表示出库任务，typei＝0时表示堆垛机在出入库台等待任务指令；toi表示目标储位编码，toi∈Z＊（正整数集）；

（3）Loci：Loci表示第i个任务的目标储位，其由所处的排列层号k，r，c唯一表示，Loci＝ （ki，ri，ci），出入库台坐标表示为：Loco＝ （0，0，0）。

1.2.2 目标函数的确立

据1.1假设，取堆垛机完成一系列任务的总行程S作为优化目标

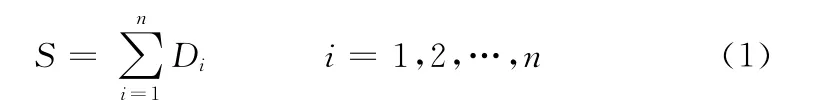
式中：Di——完成第i 个任务的作业行程，如表1 所示，归纳了其路径组成。Di与前一个任务结束储位Loci－1（当前一个任务为首个任务或出库任务时Loci－1＝Loco）、当前任务的目标储位Loci、前一个任务类型typei－1、当前任务类型typei、当前任务是否为最后一个任务 （用ξ表示，当前任务为最后任务时ξ＝1，否则ξ＝0）有关，故Di可以表示为

综合上述分析，Di的计算如下

其中，dist（Locm，Locn）表示同一仓储单元内相邻两排货架中目标储位Locm与Locn之间的距离，计算如下

1.2.3 约束域的确立

货物的存储遵循了一定的存储策略，不同的品项存放在储存区的不同区域，首先获得品项出入库约束域（MPN）：单个品项出库约束域即品项入库可行域，单个品项入库约束域即品项出库可行域。

2 单双亲混合遗传算法设计

2.1 模型编码

（1）染色体编码

染色体包括作业顺序段染色体 （seq）和目标储位段染色体 （loc），seq 和loc 采用分开独立编码方式。如图2 所示，其中seq的基因码为T 的列索引，loc的基因码对应与目标储位编码toi。

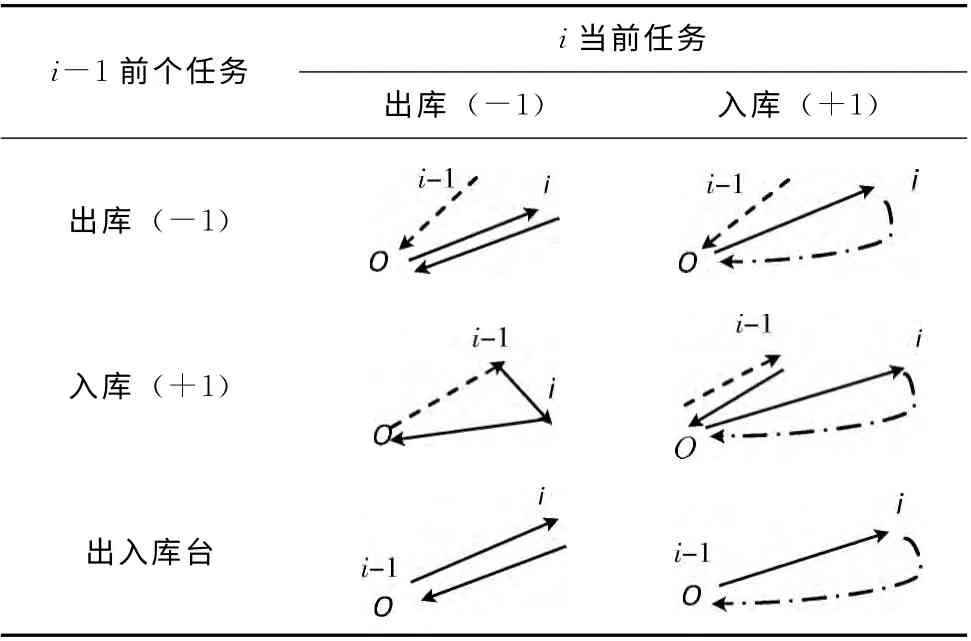
表1 Di 路径组成

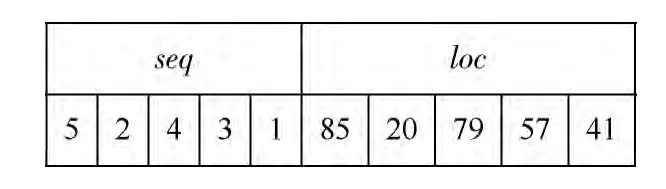
图2 染色体结构

（2）储位编码与解码

每个储位都有其唯一的地址：第k排r 层c 列，即 （k，r，c），储位编码codekrc的计算如下

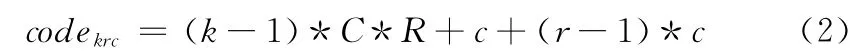
式 （2）、式 （3）中codekrc表示储位编码后的编码，MAX ＿CODE 表 示 储 位 最 大 编 码；其 中codekrc∈［0，MAX ＿CODE］，k＝0或1，r∈［0，R］，c∈［0，C］。

储位的解码过程为储位编码计算过程的逆运算，已知codekrc、R、C 可求解储位的排k、列r、层c。

2.2 适应度函数设计

适应度是用来度量种群中个体优劣的指标。本文适应度计算如下

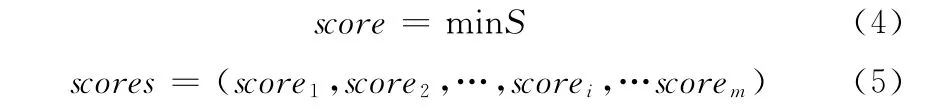
式 （4）为计算单条染色体的适应度值 （score）公式，式（5）为种群适应度值 （scores）的表达式，其中m 为种群规模，scorei表示单条染色体的适应度值。

2.3 创建初始种群

初始种群的创建过程如下：

步骤1 随机排列1到n个任务来创建seq；

步骤2 获取各品项出入库约束域MPN，按照任务矩阵T 从MPN 中随机抽取符合条件的储位，参照seq段排列储位顺序创建loc段；

步骤3 组合创建好的seq和loc 为一条完整的染色体；

步骤4 重复步骤1～步骤3，直到创建完成PopulationSize （种群规模）条染色体。

2.4 交叉算子设计

交叉算子的设计思想是，seq 采用基因重组方式；loc基因重组后再采用双亲交叉方式；图3为此过程图解，其中P11、P21为seq，P12、P22为loc。

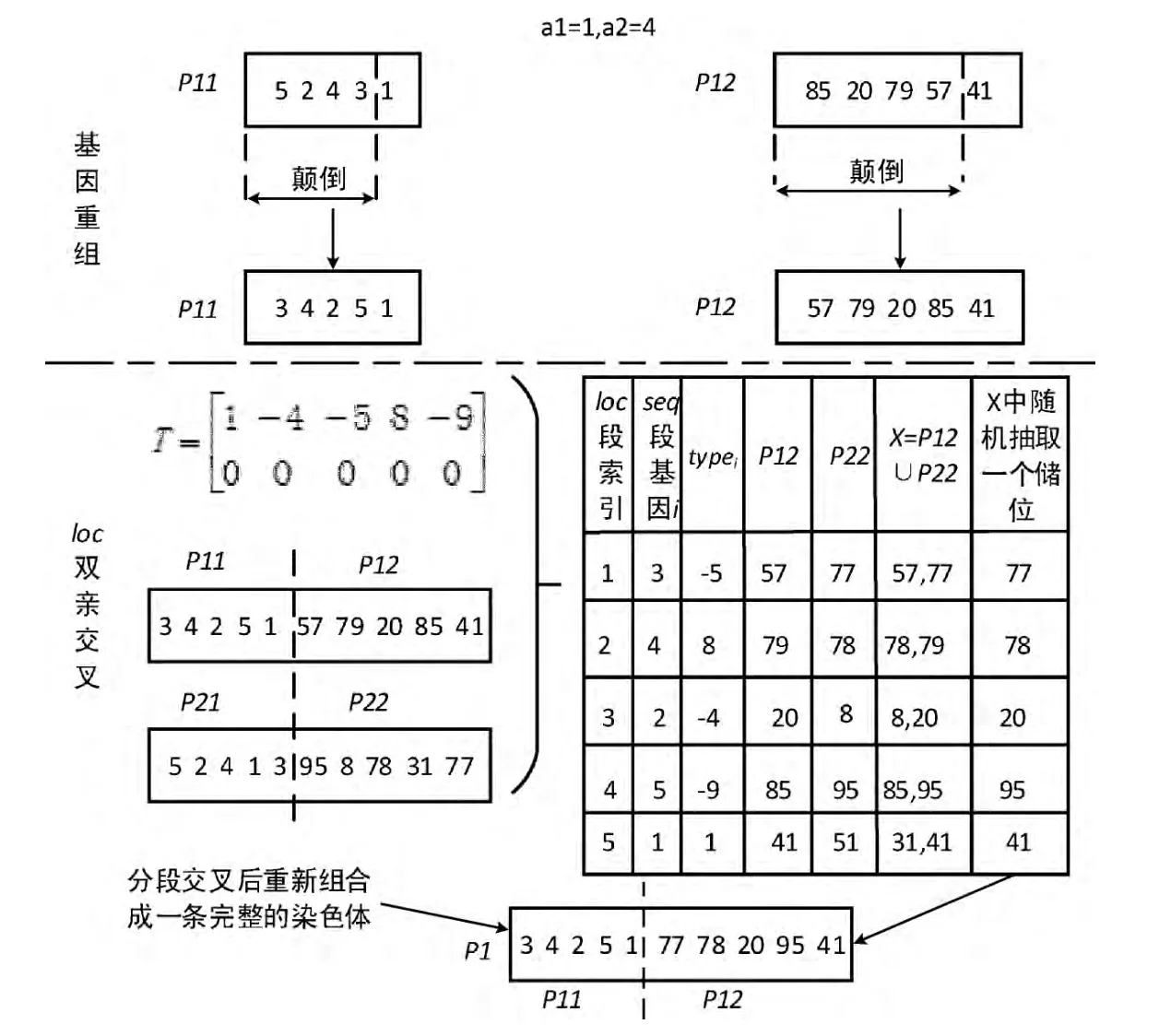
图3 交叉算子设计图解

步骤1 基因重组：选择一个父体P1，把它分段为：P11和P12，再产生两个随机位置a1、a2，分别颠倒P11和P12上a1到a2间的基因码的排列位置；

步骤2 loc双亲交叉：选择另外一个父体P2，把它分段为：P21和P22，将P22和P12上同品项作业类型的储位码toi先合并为X，再从X 中为该品项随机抽取一个目标储位，按照loc段索引生成新的P12。

步骤3 组合P11和P12为一条新的完整的染色体P1；

步骤4 重复步骤1～步骤3，直到完成所选全部父体的交叉操作。

2.5 变异算子设计

变异算子的设计思想：seq采用基因重组方式；loc采用基因重组后再单点变异方式；变异算子设计过程如下，图4为此过程图解，其中P11为seq，P12为loc。

步骤1 基因重组：选择一个父体P1，把它分段为：P21和P22，再产生两个随机位置m1、m2，交换P21和P22上m1和m2处的基因码；

步骤2 loc 单点变异：首先产生一个随机变异位置m，获得m 位置处品项的typei及出／入库可行域，取该品项的出／入库可行域与m 位置toi的差集Y，从Y 中重新为该变异位置随机抓取一个储位完成变异基因位的变异操作；

步骤3 组合P11和P12为一条新的完整的染色体P1；

步骤4 重复步骤1～步骤3，直到完成所选全部父体的变异操作。

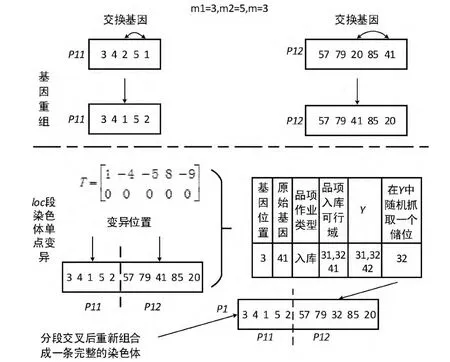
图4 变异算子图解

3 实验与分析

为了验证单双亲混合GA 对求解复杂拣选作业优化问题的有效性，基于基本GA 和单双亲混合GA，以MATLAB遗传算法工具箱为实验环境，分别进行单品项单一拣选作业、单品项复合拣选作业、多品项单一拣选作业、多品项复合拣选作业、缺货报警作业实验，最后对两种算法的优化结果及优化前后性能做了比较。实验设置如下：实验对象为一个仓储单元，由两排5层10列的货架和一条拣货通道组成。此外，本文还做了算法参数优化实验，分别测试了交叉概率 （CrossoverFraction）和种群规模 （PopulationSize）对适应度影响及种群规模 （PopulationSize）和精英个体（EliteCount）对适应度影响，其它算法参数设置见表2，算法主要参数对适应度影响实验结果如图5、图6所示。

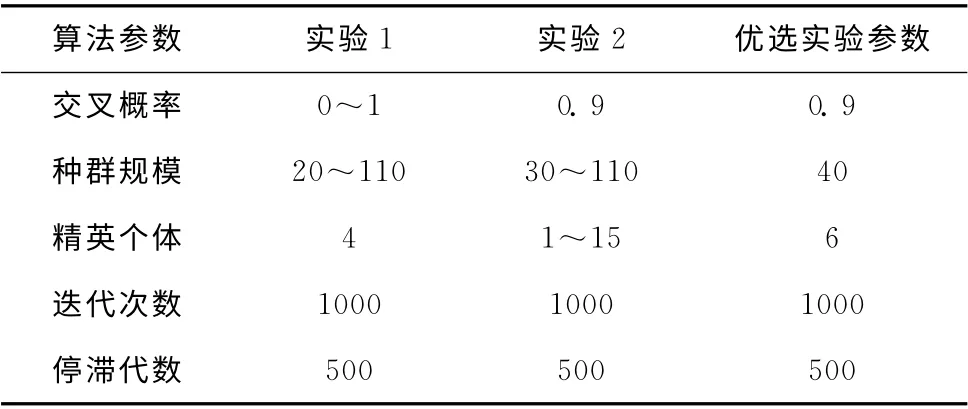
表2 实验案例算法参数设置

实验结果分析：当PopulationSize＜20，Crossover－Fraction＜0.2或CrossoverFraction＞0.95时算法不易找到最优解；当EliteCount＞6时，算法很不稳定。通过实验结果分析比较，优选的实验算法参数设置见表2第3列。

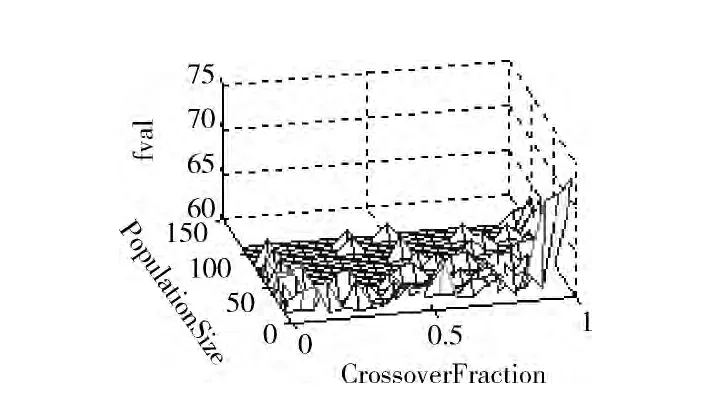
图5 PopulationSize－CrossoverFraction 测试结果

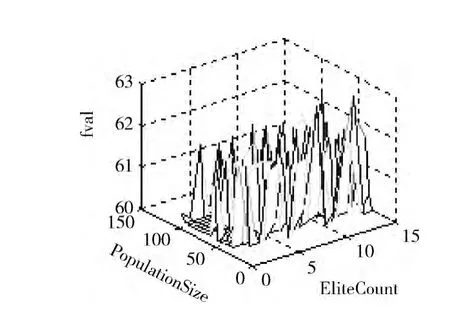
图6 PopulationSize－EliteCount测试结果

3.1 单品项单一拣选与单品项复合拣选作业实验

单品项单一拣选与单品项复合拣选作业实验，作业任务分别为：品项3的10次出库作业、品项3的5次出库和入库作业。根据下达的任务，首先搜索品项3的存储区域并寻找目标货位，然后进行组合优化，分别利用基本GA 和本文算法进行求解，优化前后性能及两种算法优化结果比较见表3。

3.2 多品项单一拣选与多品项复合拣选作业实验

多品项单一拣选与多品项复合拣选作业实验，作业任务分别为：10 种品项分别对应的一次出库作业、品项1、4、5、8分别对应的一次入库作业和品项2、3、6、7、9、10分别对应的一次出库作业。对于多品项拣选问题的优化，普通GA 不再适用。基于本文算法对多品项拣选作业问题进行优化求解，优化前后性能比较见表3，优化结果显示见表4。其中G 为优化结果输出单元数组，用于直观显示优化后作业顺序及目标储位，G1、G2分别对应于两排货架中品项及任务布局，其中，“0”代表该储位无作业任务，正整数表示入库品项，负整数表示出库品项，带圈的整数表示作业执行顺序。

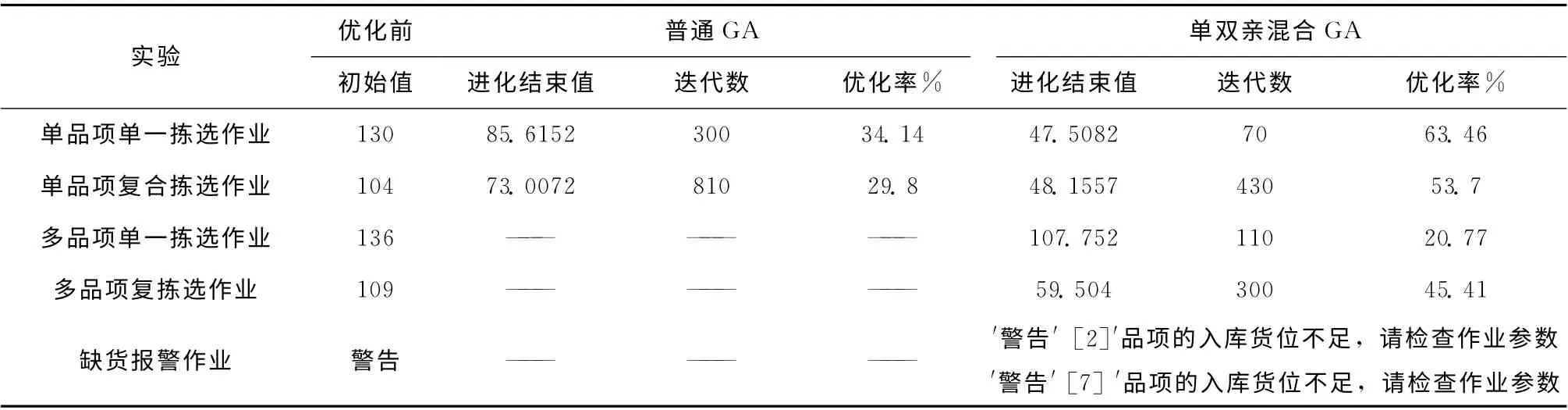
表3 拣选作业优化前后性能及优化方法比较

以上实验结果表明，构建的复杂拣选作业优化模型更贴近于实际仓储作业情况，单双亲混合GA 算法优化效果显著。此外，所研究算法已经在企业仓储管理与监控软件中得到了应用，且取得了良好的应用效果。

4 结束语

本文在多品项约束条件下，建立了复杂拣选作业数学模型，在获得多品项不同出入库约束域的基础上，兼顾作业顺序及储位优化，提出了一种单双亲混合GA 仓储作业优化算法，并用实验验证了该算法的有效性。本文仅对配送中心单个储物单元的复杂拣货作业优化问题进行了研究，对于多巷道联合作业间的作业量平衡问题，在此基础上，遵循 “出库频率高和关联度高的品项储存在不同拣货巷道”的原则，对多个仓储单元的作业优化进一步研究。

［1］LI Shizhen.Study on optimal design and control of order pic－king in distribution center［D］.Chengdu：Southwest Jiaotong University，2008 （in Chinese）.［李诗珍.配送中心拣货作业优化设计与控制研究 ［D］.成都：西南交通大学，2008.］

［2］LIU Wanjun，HUANG Yangbo，DING Peng.Optimized research on order picking based on partheno－genetic algorithm［J］.Journal of Computer Applications，2010，30 （11）：2891－2893 （in Chinese）.［刘万军，黄杨波，丁鹏.基于单亲遗传算法的拣选作业优化研究 ［J］.计算机应用，2010，30（11）：2891－2893.］

［3］JIN Meng，MU Xihui，DU Fengpo，et al.Dynamic programming and immune genetic algorithm－based multi－cross aisles order picking path planning studies［J］.Computer Measurement＆Control，2013，21 （11）：3120－3123 （in Chinese）.［靳萌，穆希辉，杜峰坡，等.基于动态规划与免疫遗传算法的多穿越巷道拣货路径规划研究 ［J］.计算机测量与控制，2013，21（11）：3120－3123.］

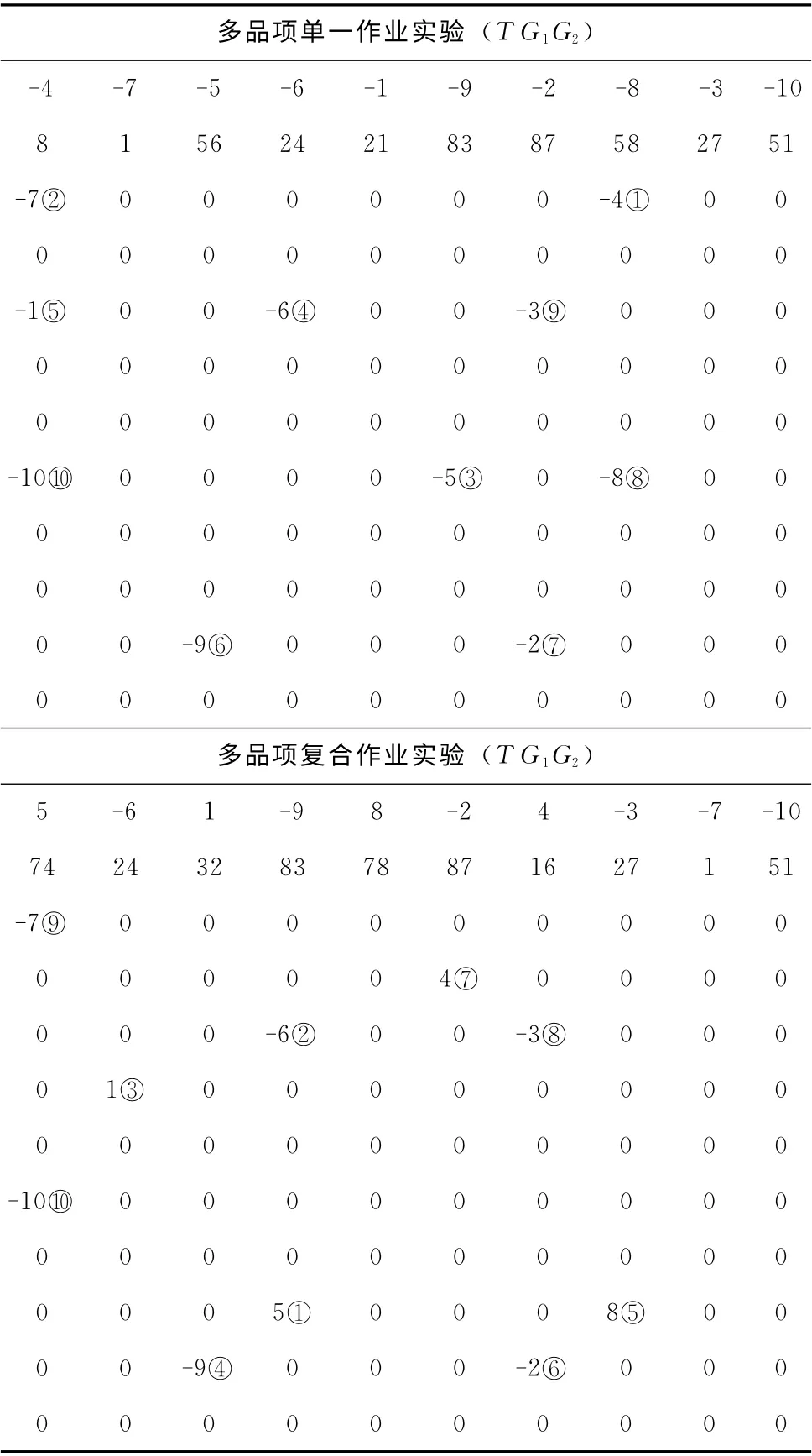
表4 实验结果

［4］PANG Long，LU Jingui.Order picking optimization of automated warehouses based on the ant colony genetic algorithm［J］.Computer Engineering ＆Science，2012，34 （3）：148－151 （in Chinese）.［庞龙，陆金桂.基于蚁群遗传算法的自动化立体仓库拣选路径优化 ［J］.计算机工程与科学，2012，34（3）：148－151.］

［5］LIU Chenqi，LI Meijuan，CHEN Xuebo.Order picking prob－lem based on ant colony algorithm ［J］.Systems Engineering－Theory ＆ Practice，2009，29 （3）：179－185 （in Chinese）.［刘臣奇，李梅娟，陈雪波.基于蚁群算法的拣选作业优化问题 ［J］.系统工程理论与实践，2009，29 （3）：179－185.］

［6］LIU Zhixiong，WANG Yafen，ZHANG Yu.Multiple population fruit fly optimization algorithm for automatic warehouse order picking operation scheduling problem ［J］.Journal of Wuhan University of Technology，2014，36 （3）：71－77 （in Chinese）.［刘志雄，王雅芬，张煜.多种群果蝇优化算法求解自动化仓库拣选作业调度问题 ［J］.武汉理工大学学报，2014，36 （3）：71－77.］

［7］Christophe Theys，Olli Braysy，Wout Dullaert，et al.Using a TSP heuristic for routing order in warehouse ［J］.European Journal of Operational Research，2010，200 （3）：755－763.

［8］FANG Yanjun，XIE Yijing.Optimization for order picking of metrological verification warehouse based on MMAS ［J］.Engineering Journal of Wuhan University，2013，46 （5）：645－658 （in Chinese）.［方彦军，谢宜净.基于MMAS算法的计量检定中心仓储堆垛机拣选路径优化 ［J］.武汉大学学报 （工学版），2013，46 （5）：645－658.］

［9］WANG Zhanlei.Research on order batching and picking path optimization problem in distribution center ［D］.Changchun：Jilin University，2013 （in Chinese）.［王占磊.配送中心订单分批及拣货路径优化问题研究 ［D］.长春：吉林大学，2013.］

［10］ZHOU Chao.Stduying on the three－dimensional warehouse storage spaces and picking routin ［D］.Ma’anshan：Anhui University of Technology，2013 （in Chinese）.［周超.企业立体仓库储位及拣货路径优化研究 ［D］.马鞍山：安徽工业大学，2013.］

［11］ZHOU Jun，ZHAO Changyou，LIU Zhanqiang，et al.Operation optimization of storage and retrieval for stacks in AS／RS of raw tabacco material［J］.Computer Integrated Manufacturing Systems，2009，15 （4）：772－776（in Chinese）.［周军，赵长友，刘战强，等.烟丝原料立体仓库堆垛机出入库作业优化研究［J］.计算机集成制造系统，2009，15 （4）：772－776.］

［12］ZHANG Xiaochuan.Modern logistics technology and equipment［M］.Beijing：Chemical Industry Press，2013：37－38（in Chinese）.［张小川.现代仓储物流技术与装备 ［M］.北京：化学工业出版社，2013：37－38.］