改进趋近率滑模控制在APF中的应用实现

李云祥，沈志达，郑 丹

（中国航天科工集团第二研究院706所，北京100854）

0 引 言

APF的电流跟踪控制方法一直以来都是国内外的一个研究热点，目前常见的控制方法有：①滞环控制，容差带宽会影响控制的效果且开关频率不固定，不利于滤波器的设计［1，2］；②PI控制，对变化率较快的谐波信号控制精度不佳，且控制参数难以选定［3］；③重复控制，基于上一周期的信号误差对当前信号进行控制，对突变信号的动态响应较慢［4－6］等。滑模控制与传统经典的电流控制算法相比，动态响应快，有较强的抗干扰能力强，且是一种非线性的控制方法，很适合结构随开关状态变化的电路之中。然而，滑模控制有一个明显的缺点，即抖振［7］。为了削弱滑模控制中的抖振问题，提出了很多方法，有滤波法、观测器法、趋近律法等［8］。本文在研究削弱抖振的趋近律法的基础上，提出了一种改进趋近律法的滑模控制方案，通过选择适当的状态变量，合适的系统参数，通过Simulink进行仿真实验，实验结果表明，此控制方案不仅可行，而且较常规的滑模控制算法有较好的控制效果，到达了预期的结果。

1 有源电力滤波器的数学模型

有源电力滤波器的原理拓扑结构如图1 所示［9］。通过有源电力滤波器工作的基本原理，参见文献 ［10］可知，有源电力滤波器主要有指令电流计算电路和指令电流生成电路两部分组成，而控制算法直接影响指令电流生成电路的输出结果。

图1中，iSa、iSb、iSc分别是系统ABC三相源电流，iLa、iLb、iLc是三相负载电流，ia、ib、ic 是APF的三相补偿电流，La、Lb、Lc是三组连接电感，Usa、Usb、Usc 是三相源电压，Udc为直流侧母线电压，由基尔霍夫电压和电流定理可得

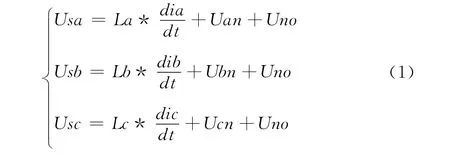
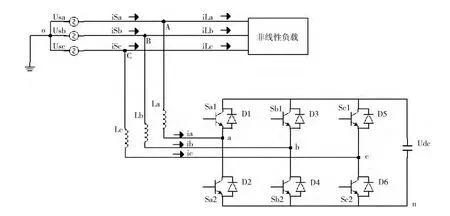
图1 APF系统拓扑结构

定义系统的开关函数为

式中：k＝a，b，c。

设系统三相对称且平衡，由式 （2）可得

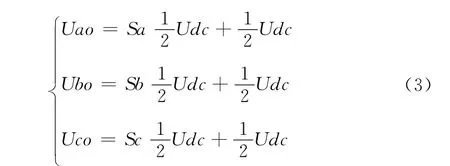
将式 （3）带入到式 （1）中可得

令

则式 （4）可以表示为

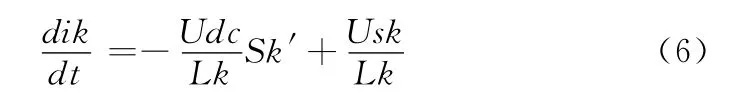
三相系统的方程只有两项是独立的，将abc 三相坐标系转换为αβ 静止坐标系有

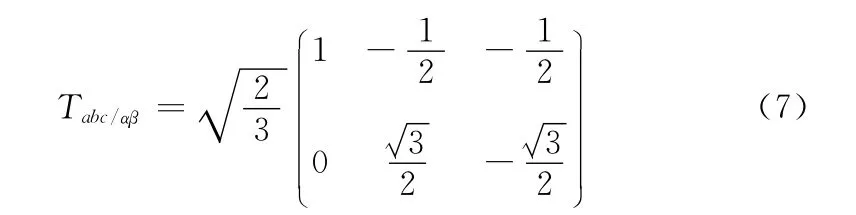
将式 （7）带入式 （6）可得系统两相静止坐标系下状态空间方程为

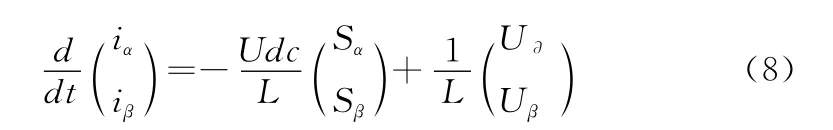
2 滑模控制

滑模控制是从变结构系统的控制中得到和发展的一种非线性控制方法，它包含一个不连续的状态反馈控制率，该控制率根据系统状态变量的变化在系统的状态空间内的两个连续的系统结构之间高频的切换，以达到被控系统的动态能够精确地跟踪预先设定的期望状态［11］。

若有一个切换面S（x）＝0的所有点都是终止点，即系统运动到切换面S（x）＝0附近时，从切换面的两侧趋近切换面，当系统在预先设计的滑模面上运动，无论系统的初始状态从哪里开始，都会被吸引到该区域，最终停留在切换面上［12］。切换面S（x）＝0上的所有点组成的状态空间区就是滑动模态区，切换面S（x）＝0就是滑模切换面，系统在滑模区的运动就称作 “滑模运动”。系统能够运动到切换面S（x）＝0，必须满足下列式子

滑模运动首先要存在切换面，系统能够趋近并且能够达到该切换面，然后沿着该切换面运动到预先设定的平衡点。其次，滑模运动必须要满足终止点的条件，即系统运动的初始点无论在状态空间的任何位置，系统的运动必须朝向切换面S（x）＝0，并且在有限的时间内能够到达切换面。

（1）设计切换面函数s（x），使滑动模态渐近且稳定。

上述切换函数S（x）和控制函数u（x）都得到后，一个完整的滑模控制系统就实现了。

3 基于趋近律的滑模控制

整个滑模控制的运动轨迹分为两个部分：趋近运动状态，即系统的运动点由任意初始位置向切换面S（x）＝0趋近的运动，图2中的AB段；滑模运动状态，即系统运动点沿着滑模面向预定平衡点运动，图2中的B0段。

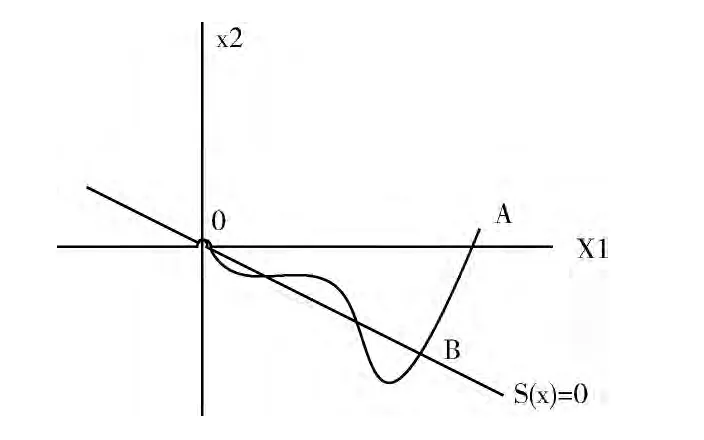
图2 滑模控制运动轨迹

滑模控制的理想条件是不考虑系统在滑模切换面S（x）＝0两侧切换过程的空间以及时间滞后，且控制量没有限制，在理想条件下，系统在滑模控制下的运动是光滑并且渐近稳定于原点，就不会产生抖振。但是在实际的条件下，由于系统状态存在时间以及空间的滞后，不可能根据控制信号做出及时快速的响应，系统的运动只会在原有滑模切换面两侧的光滑切换过程中叠加锯齿状的轨迹，如图3所示。

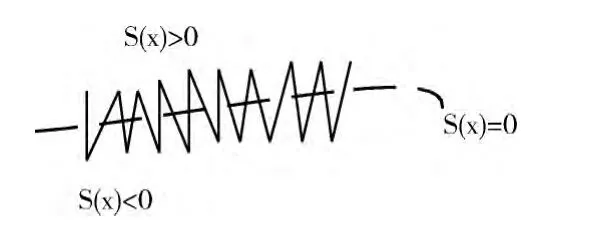
图3 抖振曲线

产生抖振的原因从物理上讲，是由于系统的状态点由初始点A 向滑模面S（x）＝0趋近运动，到达B点时，存在一定的速度和惯性。如果存在某种趋近运动，当系统的运动点远离切换面时，有较大的速度，迅速的趋近去换面S（x）＝0，在系统的运动点向切换面运动的过程中，速度越来越小，当运动点到达切换面时，速度接近于零，这样不仅保证了滑模控制的动态特性，而且还削弱了系统的抖振。

由常规的趋近率可以看出

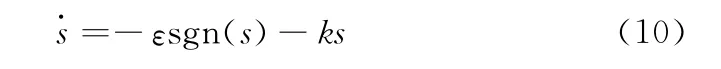
采用趋近率的滑模控制算法的趋近速度不是恒定不变的，当系统远离滑模面时，速度较大，之后，速度逐渐变小，当S →0时，趋近速度等于ε，如果ε选取合适，这样不仅缩短了趋近时间，而且减小了系统运动到滑模面时的速度，在明显的改善系统的动态特性的同时也削弱了抖振的影响。

根据趋近律的设计原则，在常规趋近律基础上，设计改进趋近律为

与常规趋近律相比可知，当系统远离切换面时，即｜S｜0时，趋近运动的速度与S2成正比，速度更大，系统可以在更短的时间内到达切换面；当系统接近切换面时，即S→0时，S21，系统的速度等于εs2，趋近速度更小。综上所述，改进趋近律不仅可以改善趋近运动的动态特性，趋近时间更短，而且还可以明显的削弱由于速度造成的系统抖振。

与此同时，当s＞0时

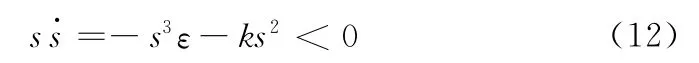
当s＜0时

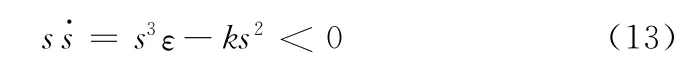
由式 （12）、式 （13）可知，改进的趋近律同样满足滑模控制可达性的条件≤0。

有源电力滤波器的控制问题，属于电流的跟踪控制问题，根据滑模控制理论，定义滑模切换面

则，切换函数为

由式 （8）可得

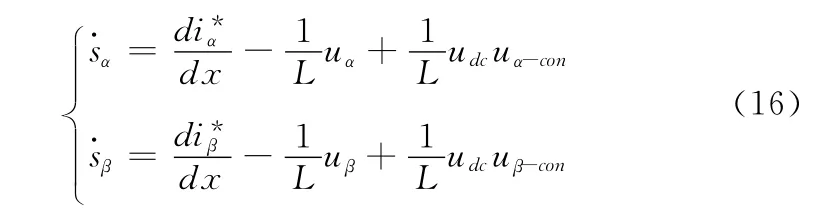
其中，uα－con，uβ－con是α，β两相的控制信号，可设

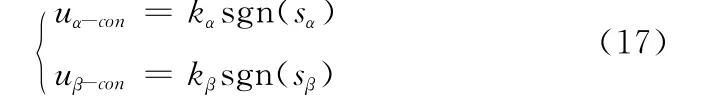
其中，sgn（x）是符号函数，当x ＞0 时，sgn（x）＝1，当x ＜0时，sgn（x）＝－1。

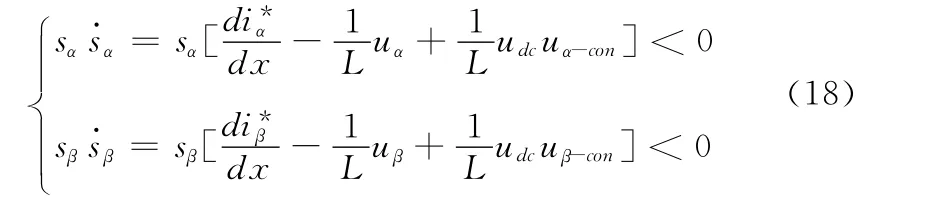
可以得出

根据式 （19）选取合适的参数带入到式 （18），就得到了滑模控制的控制量，通过PWM 或者SVPWM 调制得到相应的开关量，控制IGBT 等开关设备，以实现电流跟踪控制的效果。

4 仿真实验结果

本文通过Matlab建立APF 系统的仿真模型，仿真的条件是：三相电压380V，频率50Hz，电感L＝1mh，负载为三相整流桥。为了单纯的验证前文所提出的电流控制算法的效果，将直流侧电压Udc固定在800V，以排除直流侧电压控制的影响。

三相负载电流的波形如图4所示，负载电流发生明显的畸变，由标准的三相正弦波变为“兔耳朵”形，以A相为例。

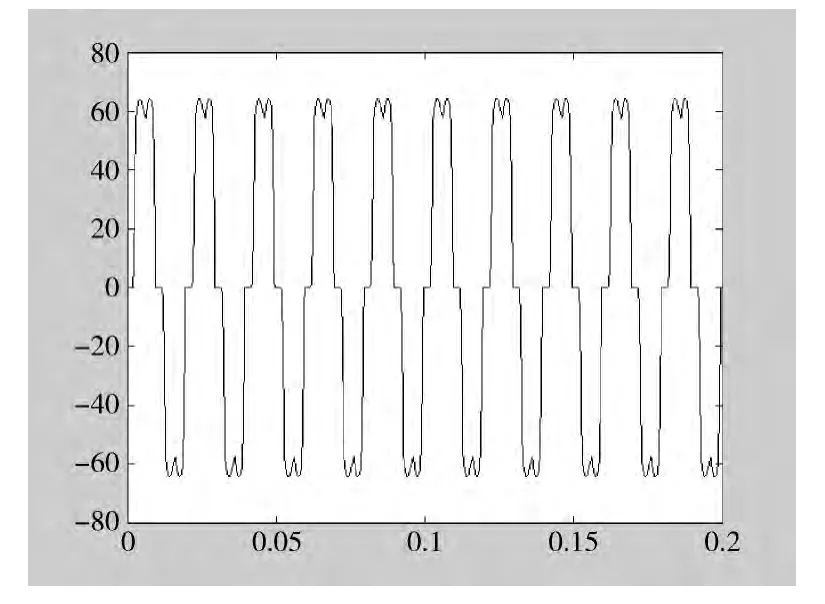
图4 负载电流波形

对三相的负载电流进行FFT 分析，分析的结果如图5所示，负载电流的总畸变率THD＝24.02%，主要存在5、7、11、13等次谐波。

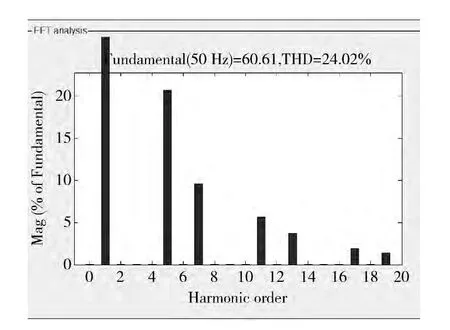
图5 负载电流FFT 分析

为了验证本文所提算法，在相同的条件下，对常规趋近律以及改进的趋近律的滑模控制算法进行仿真的结果进行对比，以A 相为例，图6 是谐波补偿后A 相的负载电流，从图中可以看出，二者都可以明显的改善负载电流的波形，改进趋近律的滑模控制算法补偿后负载电流的纹波更小、更光滑，结果接近于正弦波。

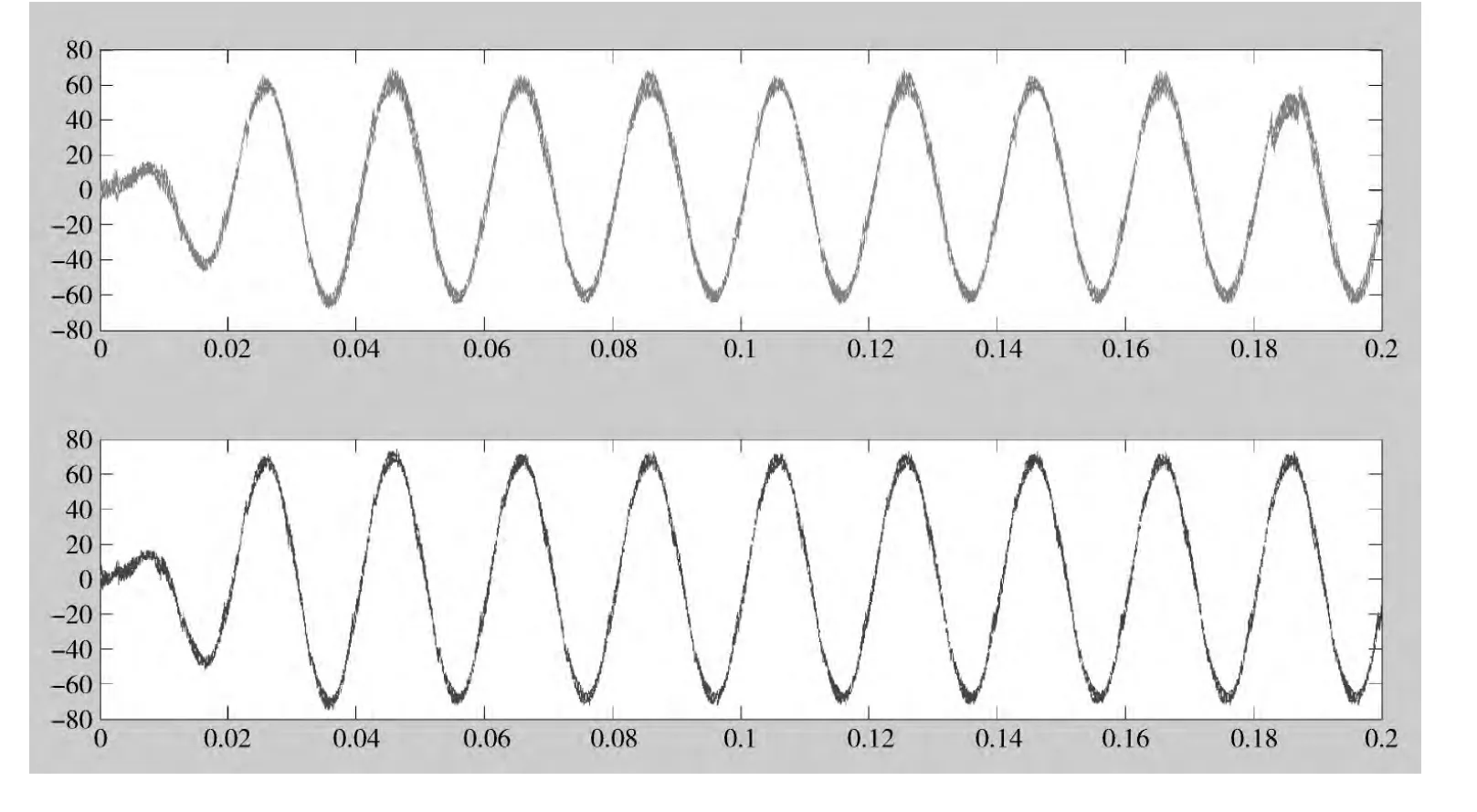
图6 谐波补偿后A 相负载电流

由图7可知，常规趋近律将负载电流的畸变率由THD＝24.02%下降到THD＝6.60%，由图8可得改进趋近律的谐波滤除效果，将负载电流的畸变率由下THD＝24.02%降到THD＝4.76%，比常规趋近律的补偿效果更好。

图9、图10分别是常规趋近律和改进趋近律的谐波跟踪图，上图曲线为谐波，下图曲线为谐波补偿电流，对比图9和图10可知，改进趋近律的滑模控制算法跟踪谐波电流更精准，抖振较小。

5 结束语

本文对有源电力滤波器的滑模控制算法进行了研究并建立了Matlab 仿真模型，针对当前滑模控制算法存在的“抖振”问题，以趋近律方面为切入点，对传统常规趋近律做了改进，与常规趋近律的滑模控制算法进行对比仿真验证，仿真结果表明，改进趋近律的滑模控制算法在APF系统上的可行的，在相同的条件下，谐波跟踪更精确，补偿后的三相负载电流的纹波更小，负载电流畸变率由常规趋近率的6.6%，下降到4.76%，补偿效率提高28%，谐波补偿的效果更好，具有一定的研究和实用价值。

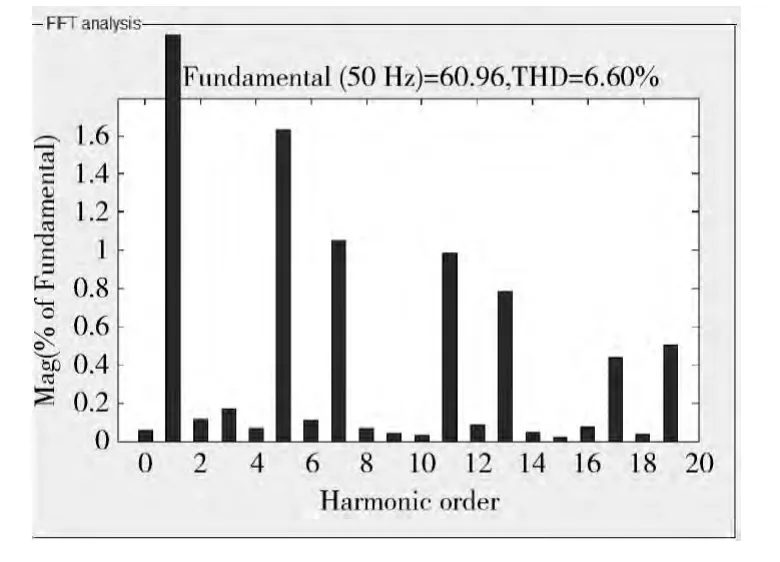
图7 常规趋近律的谐波滤出效果

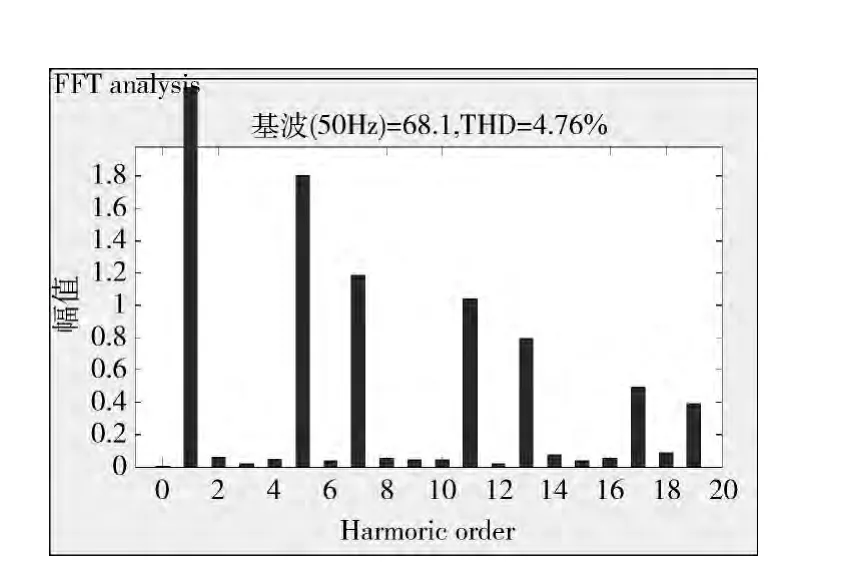
图8 采用改进趋近律的谐波滤除效果

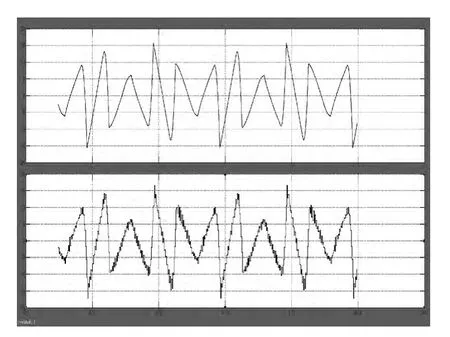
图9 常规趋近律谐波跟踪

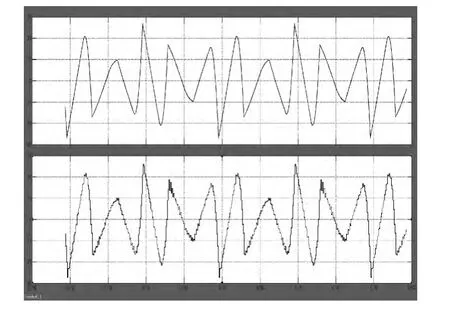
图10 改进趋近律谐波跟踪

［1］XIE Bingruo.Research on a new series hybrid active power filter and some related problem ［D］.Wuhan：Huazhong University of Science and Technology，2010 （in Chinese）.［谢冰若.新型串联混合型有源电力滤波器及相关问题研究 ［D］.武汉：华中科技大学，2010］

［2］LU Feng，TIAN Mingxing，ZHU Qianghua，et al.Comparison of indeterminate frequency hysteresis SVPWM control and hysteresis control for shunt active power filter［J］.Journal of Power Supply，2014，13 （5）：19－27（in Chinese）. ［卢锋，田铭兴，朱强化，等.并联有源电力滤波器不定频滞环SVPWM 控制与滞环控制的比较［J］.电源学报，2014，13 （5）：19－27.］

［3］ZHOU Kaijie.Reacher on active power filter ［D］.Jinan：Shandong University，2011 （in Chinese）.［周凯杰.有源电力滤波器的研究 ［D］.济南：山东大学，2011.］

［4］LIANG Zhishan，QIU Yinfeng，WEI Xueliang.Research on passivity－based control of APF with repetitive control compensation ［J］.Electric Machines and Control，2013，17 （7）：87－93 （in Chinese）. ［梁志珊，邱银锋，魏学良.重复控制补偿的有源电力滤波器无源控制 ［J］.电机与控制学报，2013，17（7）：87－93.］

［5］ZHENG Dan.Research on harmonic detection and control method of active power［D］.Beijing：Beijing Jiaotong University，2007 （in Chinese）.［郑丹.并联型电力有源滤波器的谐波检算及控制策略研究 ［D］.北京：北京交通大学，2007.］

［6］TANG Xin，MA Yingzhao，LI Hongtao.Double closed－control of active filter using repetitive algorithm ［J］.Electric Machines and Control，2009，13 （S1）：67－71 （in Chinese）.［唐欣，马迎召，李红涛.基于重复控制的有源滤波器双闭环控制［J］.电机与控制学报，2009，13 （S1）：67－71.］

［7］WANG Han.Novel sliding mode control method for threephase three－wire shunt active power filter［J］.Electronic Design Engineering，2013，20 （23）：66－72 （in Chinese）. ［汪韩.新型三相三线制并联有源滤波器的滑模控制方法 ［J］.电子设计工程，2013，20 （23）：66－72.］

［8］XU Zhuang，LI Guangjun，XU Dianguo.Parallel control of generator－side converters for permanent magnet direct－drive wind power generation systems ［J］.High Voltage Engineering，2010，36 （2）：474－480 （in Chinese）. ［徐壮，李广军，徐殿国.永磁直驱风电系统发电机侧变流器的并联控制 ［J］.高电压技术，2010，36 （2）：474－480.］

［9］ZHENG Dan，LIAO Min，LIU Zhenquan，et al.Three closed loops control strategy of three－phase four－wire active power filter［J］.Power System Protection and Control，2014 （22）：95－99 （in Chinese）.［郑丹，廖敏，刘振全，等.三相四线有源电力滤波器的三闭环控制策略 ［J］.电力系统保护与控制，2014 （22）：95－99.］

［10］WANG Zhao’an，YANG Jun，LIU Jinjun，et al.Harmonic suppression and reactive power compensation ［M］.Beijing：China Machine Press，2005 （in Chinese）. ［王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿 ［M］.北京：机械工业出版社，2005.］

［11］YI Yongqiang.Research on the sliding mode servo control in deep－sea precision manipulator［D］.Wuhan：Huazhong University of Science and Technology，2007 （in Chinese）.［易勇强.深海精密作业机械手滑模伺服控制策略研究 ［D］.武汉：华中科技大学，2007.］

［12］ZHANG Dong.Synchronization of chaotic behavior and control of a class of delayed neural network system ［D］.Shanghai：Tongji University，2010 （in Chinese）. ［张栋.一类时滞神经网络系统的混沌行为与控制同步 ［D］.上海：同济大学，2010.］