基于模拟退火法的光伏阵列铺设倾角的确定

谢世龙，张海搏，张 弛，顾伟东

(中国移动通信集团广东有限公司南方基地，广东广州 510000)

在设计小型楼宇太阳能系统时，需在建筑物外表面铺设光伏电池，光伏电池组件所产生的直流电需要经过逆变器转换成220 V交流电才能供家庭使用。不同种类的光伏电池每峰瓦的价格差别很大，且每峰瓦的实际发电效率或发电量还受诸多因素的影响，如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度等。因此，在小型楼宇太阳能系统的设计中，研究光伏电池在小屋外表面的优化铺设是很重要的问题。基于贪婪算法的小型楼宇太阳能系统优化设计［1］，仅考虑了在贴附模式下光伏电池组件所带来的经济效益，但在实际生活中，电池板的朝向与倾角［2］均会影响到光伏电池的工作效率，因此选择架空方式安装可调整与阳光辐射的角度，节约电池占用面积，因而这种方式可使光伏电池会更有效率。

在架空安装方式下，其关键是光伏电池组件最佳倾角的确定。本文以光伏阵列的倾角为决策变量，以光伏阵列倾斜面上的总辐射强度最大为目标，建立非线性模型。并基于模拟退火［3］法求解出了最佳倾角。模拟退火算法与初始值无关，约束条件少，鲁棒性强，算法求得的解与初始解状态无关，而且该方法具有渐近收敛性，已在理论上被证明是一种以概率l收敛于全局最优解的全局优化算法，模拟退火算法还具有并行性。

1 准备工作

1.1 模型假定

(1)水平面总辐射强度、水平面散射辐射强度、中午时分的太阳高度角等气象数据参考北纬38°，东经112°的历年平均值。

(2)假设光伏阵列是固定式的，光伏组件不随阳光的移动而转动。

(3)不考虑天空中的散射和地面辐射部分对倾斜面总辐射强度的影响。

1.2 模拟退火算法

模拟退火法的基本思想［4］是:(1)由一个产生函数从当前解产生一个位于解空间的新解。(2)由当前解经过简单地变换，例如对构成解的全部或部分元素进行置换、互换等产生新解。(3)计算与新解所对应的目标函数差。(4)判断新解是否被接受。(5)当新解被确定接受时，用新解代替当前解，同时修正目标函数值即可。此时，当前解实现了一次迭代，可在此基础上开始下一轮试验;而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。

2 模型建立与求解

考虑到电池板的朝向与倾角均会影响到光伏电池的工作效率，选择架空方式安装光伏电池。然后，以光伏阵列的倾角为决策变量，以光伏阵列倾斜面上的总辐射强度最大为目标，建立非线性模型。

2.1 建立非线性模型

借助模型准备部分已搜索到的相关资料［3－4］:对于某一倾角固定安装的光伏分组阵列，所接受的太阳辐射强度与其倾角有关，较为简便的总辐射强度计算经验公式为

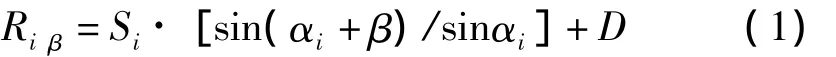
其中，Ri，β为第i日，倾斜光伏阵列面上的该日太阳能总辐射强度;Si为第i日，水平面总辐射强度;Di为第i日，水平面散射辐射强度;αi为第i日，中午时分的太阳高度角;β为光伏阵列的倾角。

建立以倾斜光伏阵列上全年的总辐射强度Rβ最大为目标，以光伏阵列倾角为决策变量的非线性模型如下

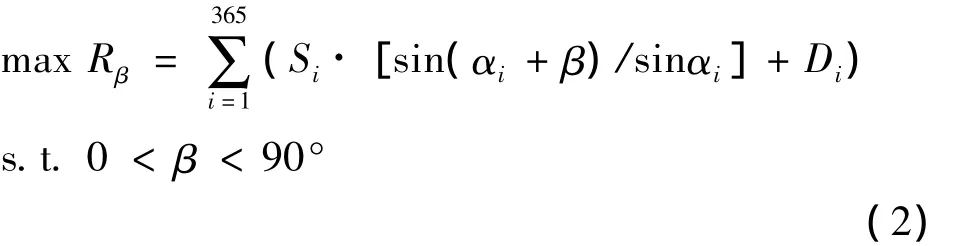
其中，Rβ为倾斜光伏阵列面上，全年太阳能总辐射强度。基于该模型可确定光伏阵列倾斜面上全年接受的总辐射强度最大时，所对应光伏阵列的最佳倾角β。

2.2 基于模拟退火算法求解模型

为求解该非线性模型，考虑采用模拟退火算法［5］对最优倾角进行搜索。解优化问题的模拟退火算法［6］是将内能模拟为目标函数值，温度演化成控制参数。由初始解和控制参数初值开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减温度值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。

令能量函数E取全年太阳能总辐射强度Rβ，初始温度为100℃，终止温度为0.3℃，降温速率为0.99，Markov链长为200。解的转移采用普遍的Metropolis准则

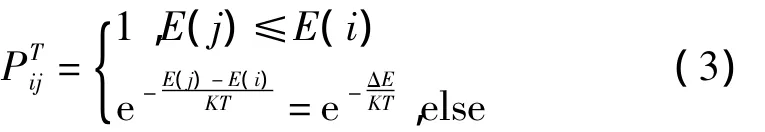
根据Metropolis准则，粒子在温度T时趋于平衡的概率为e－ΔE/(kT)，其中E为温度T时的内能，ΔE为其改变量，k为 Boltzmann常数。在温度 T，若 E(j)≤E(i)，则接受 j为当前状态;否则，以概率接受状态j为当前状态。

借助Matlab软件，采用模拟退火算法［5］确定出光伏阵列的最佳倾角β为38.5°，最大全年总辐射强度(≥30 W/m2)Rβ为1 723 800 W/m2。

图1 算法求解流程图

2.3 架空方式及贴附方式下的结果比较

在架空方式下，根据电池性能的优劣顺序及限制条件，重新对［1］中模型进行优化铺设，利用贪婪算法得出小屋外表电池铺设方案为:前顶面C1型电池32块及SN12、SN11型逆变器各1块;南面 C2型电池10块、SN3型逆变器1块;西面C1型电池10块、SN11型逆变器1块。光伏电池的寿命期为35年，假设所有光伏组件在0～10年效率按照100%计算，10～25年按照90%折算，25年后按照80%折算。从而可计算出，光伏电池的折算寿命期为

假定居民用电价格为0.5元/kW·h结合文献［1］的计算方法可以得出发电量及经济效益如表1所示。

表1 光伏电池寿命期内各面的发电量与投资情况

由表1可知，在光伏电池寿命期内，发电总量为182 493 kW·h;经济效益为47 623元，总投资为43 344元。经计算可得，年平均总收入为182 493÷31.5×0.5=2 897元;投资的有效回收年限为43 344÷2 897=14.96年;投资的实际回收年限为(14.96－10)÷0.9+10=15.51年。贴附方式下光伏组件寿命期内的发电总量为156 755 kW·h，经济效益为35 034元，实际回收年限为18.2年。相比贴附方式，架空方式下光伏组件的使用效率明显提高。

4 结束语

考虑到电池板与太阳辐射的倾角会影响到光伏电池的工作效率，本文以光伏阵列的倾角为决策变量，以光伏阵列倾斜面上的总辐射强度最大为目标，建立非线性模型［4］，并基于模拟退火法求解出了最佳倾角，利用此最佳倾角，可优化小型楼宇太阳能系统的铺设方案。大幅提升了光伏组件的效率，节约了占用面积。该方法计算过程简单，通用，鲁棒性强，适用于并行处理，简单高效地解决了复杂的非线性优化问题。利用此方法求得的最佳倾角为光伏组件的铺设及小型楼宇的设计及优化提供了理论基础。

［1］李晓飞.锁相环在光伏发电系统中的应用［J］.电子科技，2013，26(5):151 －153.

［2］韩斐，潘玉良，苏忠贤.固定式太阳能光伏板最佳倾角设计方法研究［J］.工程设计学报，2009，16(5):348 －353.

［3］唐玉珏，李淼，张建.混合GP—GA用于信息系统建模预测的研究［J］.计算机工程与应用，2004，40(25):44－48.

［4］姜启源，谢金星，叶俊.数学模型［M］.北京:高等教育出版社，2003.

［5］张军，詹志辉.计算智能［M］.北京:清华出版社，2009.