三角调频脉冲信号参数测量方法

苗雪平，张林让，雷 宇

(西安电子科技大学雷达信号处理国家重点实验室，陕西西安 710071)

三角调频脉冲信号是现代雷达电子战中常采用的一种发射信号，其具有对多普勒频移不敏感性，解决信号能量和距离分辨率矛盾的优点。测量三角调频脉冲信号参数是雷达信号处理工程领域的重点之一。传统的测量方法仅针对时域或调制域，未将时域和调制域相结合进行参数测量。且测量三角调频信号调制域参数需进行时频分析，常用的时频分析方法，如短时傅里叶变换(STFT)和Wigner－Vile分布，其在对三角调频信号时频分析时存在着诸多缺陷［1］。STFT存在着窗长和窗函数选择困难的问题，由于使用了傅里叶变换，运算量较大，且受测不准准则的限制，不能解决时间分辨率和频率分辨率的矛盾。Wigner－Vile分布虽不使用窗函数，不存在STFT的问题，但对多分量信号进行时频分布时存在着“交叉项”干扰，时频分布将变得模糊，对频率估计不准，且其采用了积分运算，运算量较大。

将三角调频脉冲信号的时域和调制域参数测量相结合，时域分析时采用统计脉冲信号包络数值的方法估计判决门限，进行脉冲个数、脉冲宽度等时域参数的测量。在时域测量结果的基础上，对三角调频信号的脉内调制参数进行测量。脉内调制参数测量采用相位差分法来得到信号的瞬时频率曲线，并进行线性拟合来获得线性度等调制域参数。其中，相位差分法首先通过反正切函数计算信号的瞬时相位，再对瞬时相位进行差分运算，直接得到信号的瞬时频率，相对于STFT，运算量大幅减小，且无窗函数，也不受测不准准则的限制。此外，相位差分法不存在Wigner－Vile分布的“交叉项”干扰问题。最后进行了Matlab仿真，仿真表明，高信噪比下该方法相对于其他方法，测量参数运算量少、误差小，适合于工程实践。

1 三角调频脉冲信号模型

三角调频脉冲信号是一种脉内频率调制信号，其指的是在脉冲宽度内频率连续线性变化，信号频率先向上后向下或先向下后向上扫描脉冲宽度。其信号表达式为

式中，rect(t)为矩形脉冲;A为三角调频信号的幅度;f0为中心频率;μ为调频系数;f0+μt或 f0－μt为瞬时频率。

2 脉冲时域参数测量

脉冲时域参数是描述雷达信号特征的重要参数，主要包括脉冲宽度、脉冲周期、上升时间、下降时间、关闭时间、占空比、脉冲幅度、幅度90%、幅度10%、顶值、底值、过冲、下冲等，各参数定义［2］。

脉冲时域参数的测量以脉冲包络为基础，设脉冲实、虚部信号分别为I(t)和Q(t)，计算信号包络的表达式为

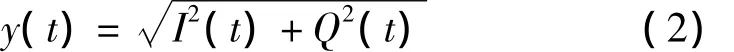
以信号包络y(t)来估计脉冲的近似幅度，关键要估计脉冲波形的近似顶值和近似底值，以获得判决门限。估计算法主要有两种:(1)密度分布平均法［3］;(2)密度分布众数法［3］。

文献［2］指出，当测量采样点数越多，在脉冲包络最大值和最小值之间均分的区间个数越多，所求得的近似底值和近似顶值越精确;通常密度分布平均法能比密度分布众数法得到更好的精度，但其运算量也偏大。

2.1 脉冲个数测量

估计出脉冲的近似顶值 topvalue'和近似底值basevalue'后，近似幅度ampvalue'表达式为二者之差。

以10%ampvalue'作为上升沿下降沿检测门限，测量脉冲个数的步骤为:

(1)脉冲个数初始化为N=0，从信号的起始位置开始查找第一个近似上升沿，查找成功标志位为flag=1，否则标志位为flag=0。

(2)查找到近似上升沿后，继续往后查找近似下降沿，查找成功标志位为flag=1，否则标志位为flag=0。

(3)查找到近似下降沿后，继续往后查找近似上升沿，查找成功后脉冲个数N=N+1，并将标志位赋值flag=1，否则标志位flag=0。

(4)重复步骤(2)至步骤(3)直到标志位flag=0，则结束。

2.2 脉冲宽度测量

在测量脉冲个数过程中，记录所有近似上升沿、近似下降沿判决时刻，对信号的某个脉冲，近似上升沿判决时刻为t'升，近似下降沿判决时刻为t'降，则计算脉冲宽度表达式为

2.3 脉冲其他参数测量

在每个脉冲的脉冲宽度内，运用密度分布平均法，计算每个脉冲精确的顶值top和底值base。并求得每个脉冲精确幅度amp为二者之差。

求出每个脉冲包络的最大值max和最小值min，则过冲overshoot为最大值max和顶值top之差，下冲undershoot为底值base和最小值min之差，幅度的90%(记为amp90%)和幅度的10%(记为amp10%)表达式为

然后通过幅度的90%和幅度的10%这两条脉冲幅度参考线，在脉冲宽度τ内查找这两条参考值所对应的时刻值，即可计算出脉冲的上升时间tr、下降时间tf，脉冲周期T，关闭时间toff及占空比dt等参数。其计算表达式为

其中，tr90是上升沿幅度90%所对应的时刻;tr10是上升沿幅度10%所对应的时刻;t't10是相邻下一次上升沿幅度10%所对应的时刻;tf10是下降沿幅度10%所对应的时刻;tf90是下降沿幅度90%所对应的时刻。由脉冲宽度τ和脉冲周期T，可计算关闭时间toff和占空比dt。

3 脉内调制参数测量

基于已估计出三角调频脉冲信号的脉冲宽度及脉冲周期，可测量其脉内调制参数，主要包括分析调频方向和测量最小频率、最大频率、中心频率、带宽、左调频系数、右调频系数、左线性度和右线性度。首先，应提取三角调频信号每个脉冲的频率，即要对信号进行时频分析。常用的时频分析方法有短时傅里叶变换方法(STFT)、Wigner－Vile分布方法和相位差分法等，本文采用相位差分法。

3.1 短时傅里叶变换

STFT利用一个时间有限的窗函数来截取信号，然后对截取信号采用傅里叶变换进行分析，以确定在这一窗时间段内存在的频率，再沿着时间轴移动窗函数，最终得到信号的瞬时频率随时间的变化关系图。研究表明STFT算法简单，且为线性时频分布，不会在频率分量之间产生交叉项干扰，但采用傅里叶变换，需多次进行积分运算，运算量较大，且由于窗函数的影响，窗长和窗函数选择困难，也无法克服时间分辨率与频率分辨率之间的矛盾［4］。因此，STFT不适合工程上三角调频信号时频分析。

3.2 Wigner－Vile分布

Wigner－Vile分布是实函数，设某实信号的解析形式为x(t)，则其Wigner－Vile分布为

从上式可看出，Wigner－Vile分布中x(t)出现了两次，且不含任何窗函数，是双线性变换，不存在时间分辨率与频率分辨率的矛盾，故具有较好的时频聚集性。但其不满足可加性，且为了得到时频曲线，需进行多次积分运算，运算量较大。经研究表明，其还会在时频平面上虚假分量的位置产生分量之间的交叉项干扰。交叉项会产生有限的能量，其反映了两个相关项之间的相关性并高度震荡，难以克服［5－6］。因此，该方法不适与多分量信号三角调频信号的时频分析。

3.3 相位差分法

假定单一分量连续时间信号s(t)解析表达式为

对于采集的离散信号可通过信号的相位差分来估计信号的瞬时频率。采用中心有限差分估计信号的瞬时频率fc(n)表达式为

其中，fs为信号的采样率;φ(n)为第n点的瞬时相位。

根据中心有限差分估计的特点，可看出其对信号的频率是无偏估计，且群时延为零，对应时频分布的一阶矩。相对于STFT，算法简单，无多次复杂的积分运算，仅有一次反正切运算和差分运算，运算量大幅减小，且无窗函数，也不受测不准准则的限制。此外，相位差分法不存在Wigner－Vile分布的“交叉项”干扰问题，后续的仿真结果将对此验证。故利用中心有限差分估计三角调频信号频率是有效的。

由瞬时频率曲线可得出调频方向。根据调频方向，可确定频率曲线中心为频率最大值或是最小值。以频率曲线为中心将曲线分为左、右两半部分，分别进行直线拟合，求得左、右线性度和左、右调频系数。求得脉冲宽度τ，瞬时频率最大值freqMax，频率最小值freqMin。带宽B为二者差值，中心频率f0为二者之和的

4 仿真结果

为验证时域测量方法的有效性，以三角调频脉冲信号进行Matlab仿真，参数设置为调频方式为向上调频，脉冲宽度为6μs，脉冲重复周期为16μs，完整脉冲个数为4，采样率为50 MHz，带宽10 MHz，信噪比为20 dB。根据上述方法，测得的时域参数如表1所示。

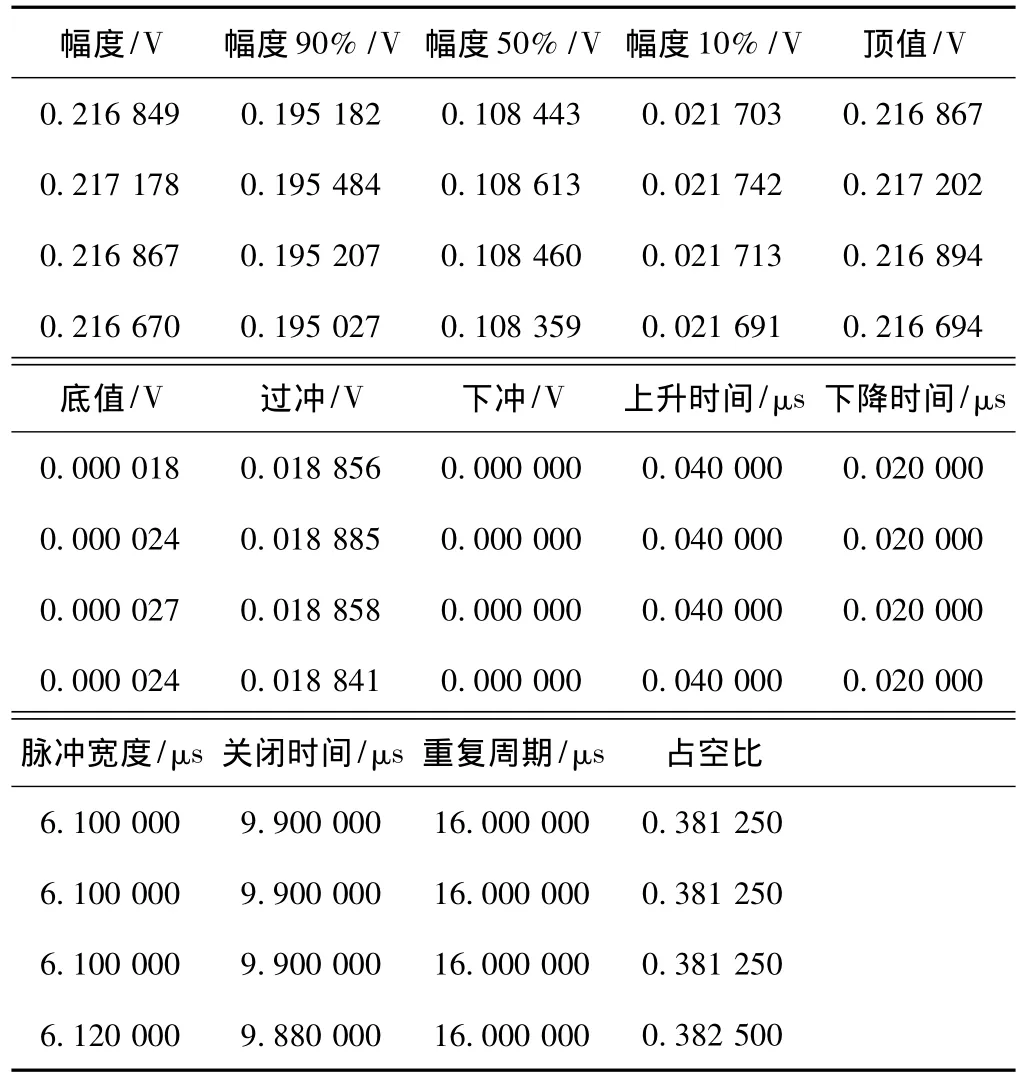
表1 三角调频脉冲信号时域参数表

从表1中可看出，测量的脉冲个数为4，脉冲宽度约为6.1μs，重复周期为16μs，上升时间为0.04μs，下降时间为0.02μs，与实际设定的参数基本上一致，测量误差小。用STFT、Wigner－Vile方法分析三角调频脉冲信号，时频分布如图1所示。

图1(a)STFT采用窗长为30的矩形窗，每次滑窗均在时频图上有明显的痕迹，STFT方法受窗长影响较大。如图1(b)所示，采用Wigner－Vile分布方法，三角调频的时频分布中间出现了“虚假”，有用的时变谱图变得模糊，因此STFT和Wigner－Vile分布均不适合分析三角调频信号。

图1 不同方法下三角调频脉冲信号的时频分布

与STFT方法仿真相同信号，信噪比为20 dB和7 dB时，相位差分法拟合曲线和理想曲线图对比如图2和图3所示。

图2 SNR=20 dB时三角调频相位差分法曲线

图3 SNR=7 dB时三角调频相位差分法曲线

由仿真结果可看出，直接根据瞬时频率的定义展开的相位差分法，具有算法简单、运算量小等特点。不存在“交叉项”干扰，尤其适合工程实践上的大数据量测量，但抗噪性能并不理想，当信噪比较小时，测量性能较差，因此更适用于高信噪比的信号。

将算法用Matlab仿真200次，测量所得各脉内调制参数如表2所示。

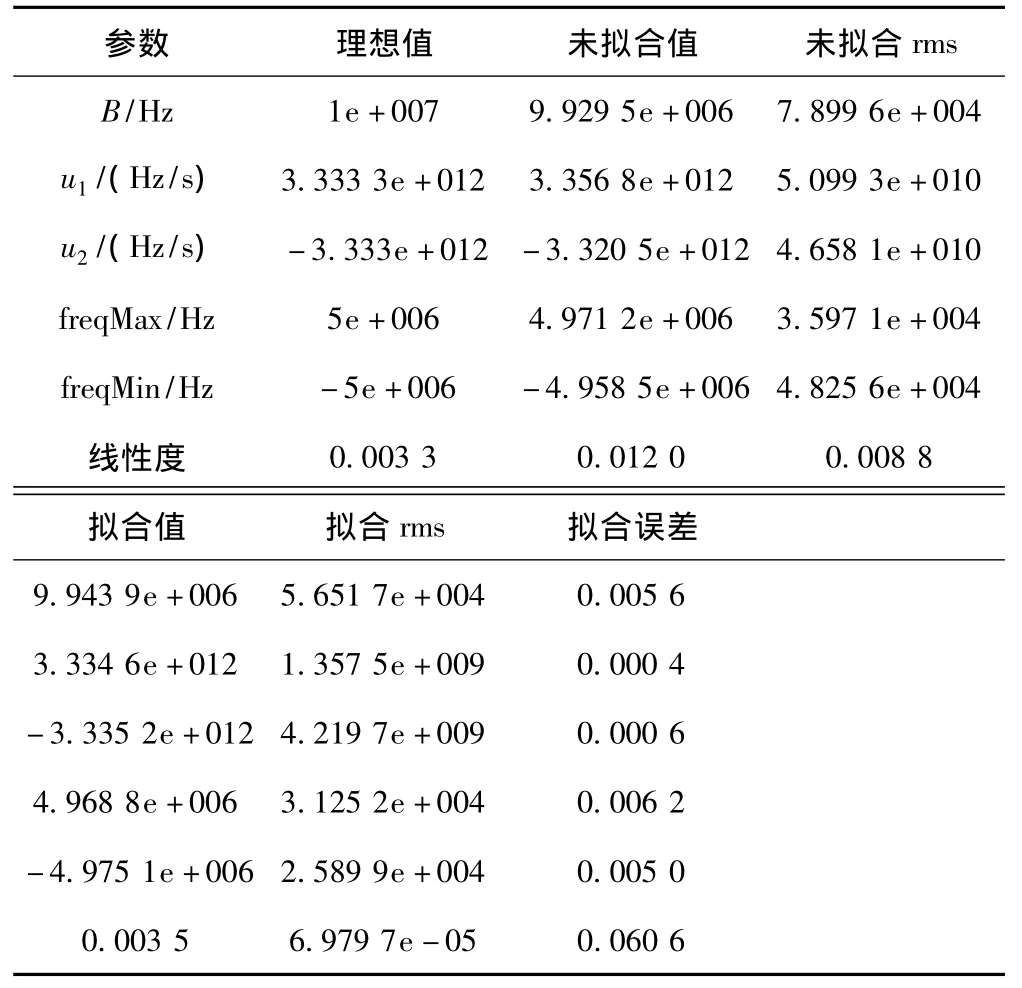
表2 三角调频脉冲信号脉内调制参数表

其中，B表示带宽;u1、u2分别表示左、右调频系数;freqMax、freqMin分别表示脉内最大频率和最小频率。通过测量数据可以看出，调频方向为上三角调频拟合后参数值与理想值相比，测量误差＜1%，测量效果良好。实际仿真时，Matlab仿真200次，用相位差分法，与使用STFT、Wigner－Vile分布相比，得到时频曲线的时间大幅减小。因此，相位差分法具有更小的运算量。

5 结束语

针对雷达中常用的三角调频脉冲信号、联合时域、调制域两方面测量其参数，调制域测量基于时域测量结果。在脉内调制参数测量上，舍弃受选择窗长和窗函数影响较大的STFT方法与时频分布有交叉项的Wigner－Vile方法，而采用相位差分法。仿真表明，其对于高信噪比信号，具有算法简单、运算量少、测试误差小的优点，利于工程实践的测试测量使用。

［1］刘东霞，赵国庆.脉内调制信号参数测量与分析［J］.现代雷达，2003，25(11):17 －20.

［2］郭允晟，苏秉炜，方伟桥.脉冲参数与时域测量技术［M］.北京:中国计量出版社，1987.

［3］刘明亮，陆福敏，朱江淼.现代脉冲测量［M］.北京:科学出版社，2010.

［4］Czerwinski R N.Adaptive short－ time Fourier analysis［J］.IEEE Signal Processing Letters，1997，4(2):42 －45.

［5］罗利春.用维格纳－威利时频分布进行信号时频分析［J］.航天电子对抗，2003(4):18 －21.

［6］韩中合，朱霄珣，李文华，等.基于EMD消除Wigner－Vile分布交叉项的研究［J］.汽轮机技术，2010，52(3):211 －214.