基于相位干涉仪的同时信号测向技术

刘东文，郭少华

(西安电子科技大学电子工程学院，陕西西安 710071)

相位干涉仪具有较高的测向精度以及较快的测向速度，在无源探测中得到了广泛应用。传统的相位干涉仪测向只能对单个到达脉冲信号到达多个天线的相位差来进行雷达信号到达方向的估计，故存在对同时多信号无法分辨造成测向错误的缺陷。针对这一缺点本文提出了一种具有同时信号测向能力的相位干涉仪测向方法，在干涉仪测向中引入了数字信道化技术来解决同时信号分辨，并采用多基线天线结构提高测向精度，天线间距的设计较为灵活，且算法简单、容易实现。

1 基于相位干涉仪同时信号测向原理

式中，{dk}N－1k=1为各天线阵元至0阵元(第一个基线为0阵元)的距离，也称为基线长度［1］。各基线接收到的信号分别进行数字化滤波，将滤波后接收通道0的输出信号分别与其它各通道滤波输出在同一信道内的信

图1为N基线基于相位干涉仪的同时信号的测向系统示意图，当平面电磁波从θ方向入射到线阵时，各阵元接收到的信号为号进行相关运算，输出各阵元接收信号与0阵元接收信号的正交相位差，送至相位差测量与测向处理机。

当有同时多信号到达时，可对各阵元进行FFT变换，即对各阵元的输出信号进行频域处理，并进行门限检测，实现同时多信号频域分离，根据频率标记出每个信号所在信道，这就是频域信道化。

因此，对时域重叠频域分离的信号进行测向，先进行频域分离，再分别对处在同一信道内的信号进行鉴相和测向处理的方法称为基于相位干涉仪的同时信号测向。该方法包括多相数字信道化和一维多基线干涉仪测向两大核心技术。

图1 基于相位干涉仪的同时信号的测向系统示意图

1.1 多相数字信道化技术

传统的数字信道化技术结构复杂，处理速度相对较慢且对硬件要求高，难以满足电子战侦接收机对瞬时宽带信号实时处理以及高精度测量的要求，所以引入了一种高效的数字信道化接收机系统。该数字信道化接收机系统是一种实时宽带数字接收机［2］，采用了多相滤波和短时傅里叶变换(STFT)相结合的算法结构，即多相FFT技术［3］，能实现对宽带信号的实时滤波、检测和参数测量。其优点是不仅具有较高的时频测量精度和检测灵敏度，而且数据输出率低，降低了对后续的处理系统的要求。

如图所示为多项滤波器的FFT结构，该结构的优点在于通过抽取降低STFT预算处理的速度，便于硬件实现。

图2 多相FFT模块结构简图

实现多相FFT算法结构的推导公式如下

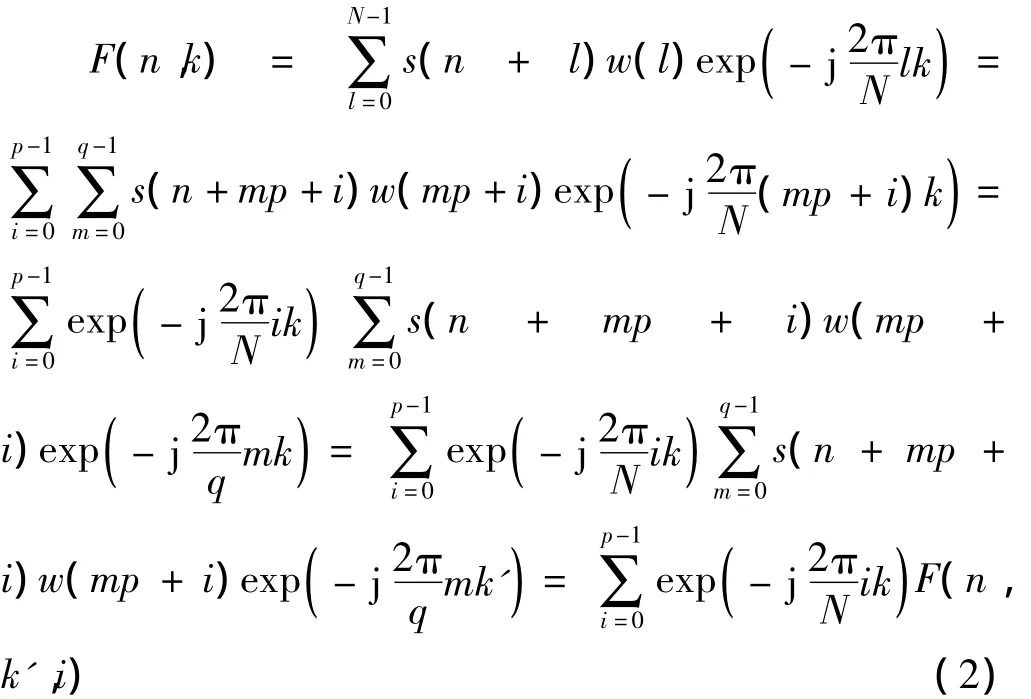
其中N=p × q，k=0，1，…，N －1，k'=mod［k，q］，p为抽取率，q 为 FFT 点数为第 i路的q点FFT的结果。图2中，wi(m)=w(mp+i)，i=0，1，…，p－1为中汉宁窗第i个多相分支的系数。

土壤溶液电导率（EC值）反映溶液中电解质的浓度，在一定程度上也反映了溶液中盐离子浓度，作为土壤盐分对作物危害的诊断指标，比以往所用的土壤全盐含量更为客观准确[10]。由表2可见，经过改良处理后，土壤EC值和pH值都比对照有所下降。改良区和对照区的EC值都属于正常范围，其中改良区的EC值比对照区下降了0.32 ms/cm；改良区的pH值比对照区下降了0.49。说明本改良处理可以促进耕层土壤脱盐，降低盐离子浓度，同时降低土壤pH值，改善耕层土壤的酸碱度。

在图2所示的算法结构中，一帧数据(长度为N)被抽取为p路，每路q个点，加窗后通过q点的FFT模块后再进行q点串行p路并行的合成滤波，其中第i路的合成滤波器结构如图3所示。合成滤波器以先进先出(FIFO)方式，q点串行p路并行输入输出。

图3 第i路的合成滤波器结构图

多相FFT模块可分批分次地对不连续的p个信道同时进行检测，例如对第 0，p，2p，…，(q －1)p 号信道同时并行检测，然后接着对第1，p+1，2p+1，…，(q+1)p+1号信道进行同时并行检测，以此类推，最后对第 p－1，p+p－1，2p+p－1，…，(q－1)p+p－1号信道同时并行检测，1帧数据共需要进行q次同时并行检测才能完成N个信道的检测。因为算法采用多路并行结构，所以多相FFT模块的数据处理速度和数据输出率等同于任意一路的数据处理速度和数据输出率。对于某一路而言，q点的FFT的运算量比N点FFT的运算量小得多，所以处理速度快很多，同时多相FFT模块的单路输出数据率降为STFT模块的1/p，因此实时性和低输出数据率都得到保证。

1.2 一维多基线相位干涉仪测向技术

一维线阵干涉仪测向系统的组成如图3所示，当平面电磁波从θ方向入射到线阵时，各阵元接收到的信号为

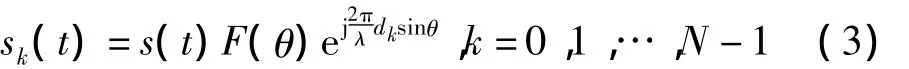
式中，{dk}N－1k=1为各天线阵元至0阵元的距离，也称为基线长度。接收通道0的输出信号分给其他各通道的相关器，输出各阵元接收信号与0阵元接收信号的正交相位差至相位差测量与测向处理机。

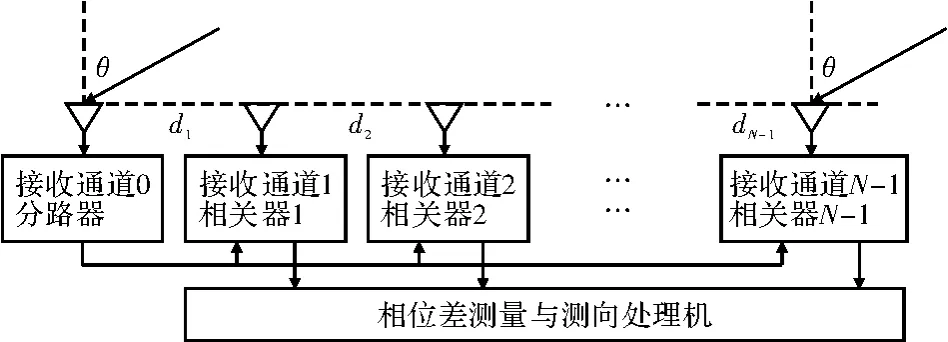
图4 干涉仪系统结构

相位差测量与测向处理机首先测量各基线有模糊的相位差{φk(t)}N－1k=1，φk(t)∈［－π，π)，∀k

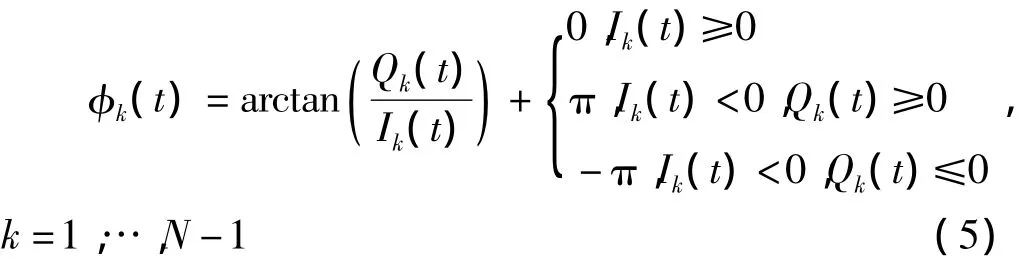
然后再利用长短基线的关系，对{φk(t)}N－1k=1解模糊和相位校正，计算信号的到达方向θ。

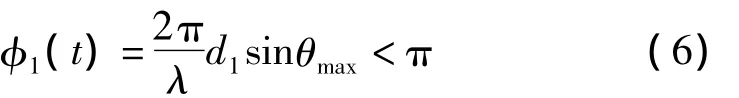
假设最短基线长度d1与单侧最大测向范围θmax满足式(6)，此时相位差φ1与方向θ具有单调对应关系，可以通过式(7)求解信号的到达方向

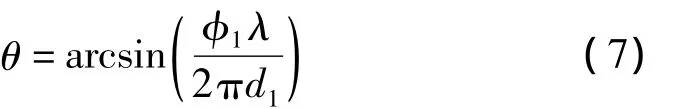
由于长基线解模糊后的相位误差较小，可由短基线求得的无模糊相位逐级求解长基线的无模糊相位{(t)}N－1k－1，并进行相位校正

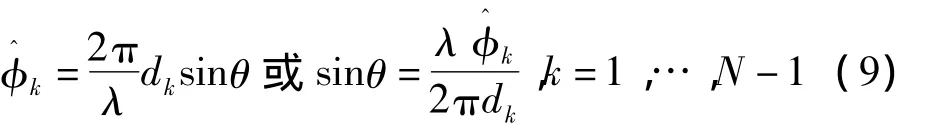
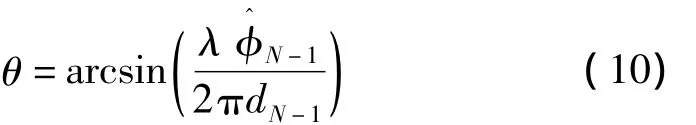
根据最优估计理论，应该要求估计量与实测值的误差平方最小，即

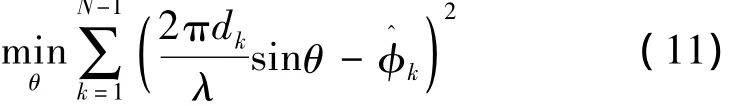
对式(11)中变量θ求导，并令导数为0，可得到方向的最小二乘估计

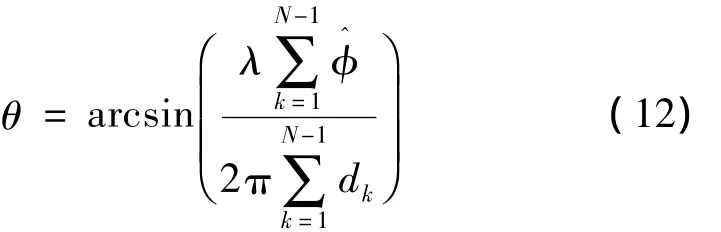
对式(12)中的各参量求全微分，可得到其对测向误差的影响

这表明，在基线方向(θ=±π/2)误差发散，不能测向;dk/λ越大误差越小;此外应尽可能减小频率抖动、基线抖动和系统的相位误差。

由式(8)的相邻解模糊和相位校正算法可见，短基线的相位误差会被放大相邻基线比，然后再进入相邻长基线的解模糊计算，如果放大后的上级相位误差与本级相位误差之和达到π以上，就会发生解模糊错误，且会传递到下一级。因此，要求各级的相位误差必须满足

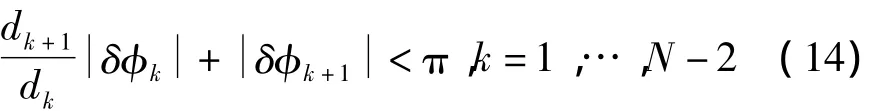
假设各级相关器的相邻基线比与最大相位误差都一致(dk+1/dk=n，δφkmax=δφmax，∀k)，则式(14)可简化为

在实际系统设计中，应按照系统能够达到的相位误差δφmax来选择合适的相邻基线比n。

2 计算机仿真

考虑到脉冲流密度以及信号处理能力的限制，假定在各种噪声条件下同时接收到3个脉冲信号，频率分别为1.2 GHz，2.3 GHz和3.5 GHz，信号到达角分别为10°，22°和30°，根据上述原理进行仿真。

如图5所示，改测角方法能够较为准确地测量出信号的到达方向角，且有一定的同时信号分辨能力;图6所示，对3个信号角度测量的误差随信噪比(SNR)变化，当SNR＞2 dB时，测量精度基本保持在0.01以下，满足电子侦察机对角度测量的要求。图7表示了单信号载频1.2 GHz，入射角为1°～90°时对测量结果的影响。

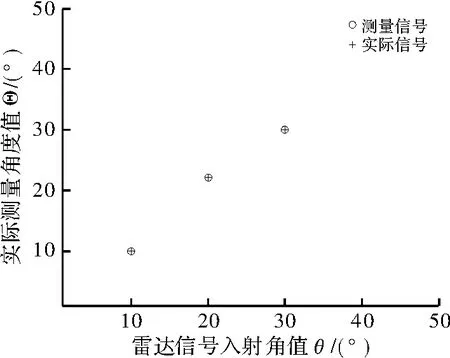
图5 同时信号到达角度测量示意图

图6 测量误差与SNR的变化曲线

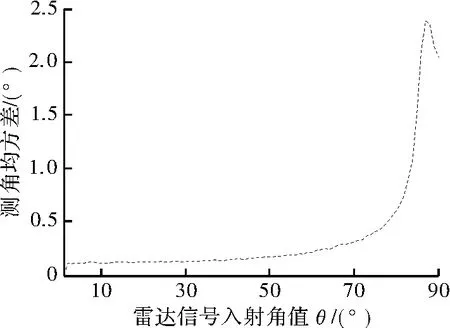
图7 入射角与测量角的均方差之间的线性关系

从图中可看出，不同当来波信号的入射角度比较小时，相应的测角误差也会变较小，随着入射角度的增加，测角的误差也会呈现相应的增加趋势。仿真结果验证了入射角度在(0°，60°)测角误差相对较小，这与实际测量中测角范围在(－60°，60°)内吻合。

3 结束语

通过仿真可分析出，基于相位干涉仪的同时信号测向有效解决了传统相位干涉仪对时域重合频域分离同时到达信号的分辨问题，具有一定的同时信号分辨能力，该方法利用多相数字信道化的高效结构，降低了系统的复杂度，处理时间满足实际的电子侦察机境要求，并采用多基线干涉仪提高了测向精度以及解模糊的正确率。由此可见该方法能够有效完成电子侦察任务。

［1］赵国庆.雷达对抗原理［M］.西安:西安电子科技大学出版社，1999.

［2］王宏伟，赵国庆，王玉军，等.一种宽带数字信道化接收机［M］.西安电子科技大学学报:自然科学版，2010，37(3):487－491.

［3］胡来招.雷达侦察接收机设计［M］.北京:国防工业出版社，2000.

［4］刁晓静.电子侦察中的宽带DBF技术研究［D］.西安:西安西安电子科技大学，2011.

［5］余建宇，王超，郑先宝.一种相位干涉仪的数字信道化测向方法［J］.火控雷达技术，2011，40(1):60 －63.

［6］蒋学金，高遐，沈扬.一种多基线相位干涉仪设计方法［J］.电子信息对抗技，2008，23(4):39 －45.

［7］Wu D Z.Analysis of signals and linear systems［M］.Beijing:Higher Education Press，2004.

［8］丁鹭飞，耿富录，陈建春.雷达原理［M］.4版.北京:电子工业出版社，2009.