一种低损耗波导高通滤波器的设计方法
2015-12-20寇阳
寇 阳
(中国电子科技集团公司第54研究所卫星通信与广播电视专业部,河北石家庄 050081)
在卫星通信频率分配时,为了减小临星干扰,一般上行链路都采用频率较高的频谱资源[1],如目前逐步进入商业运营阶段的Ka频段卫星通信系统,其上行链路工作频率(29~30 GHz)较下行频率(19.2~20.0 GHz)高约 10 GHz[2]。当天线收发隔离度固定时,发射机输出的下行频率热噪声将与下行信号一起进入接收设备,可能会降低通信系统的接收性能,甚至导致整个系统无法正常工作。
在发射机输出口安装抑制下行频率热噪声的阻收滤波器后,该阻收滤波器的插入损耗会直接导致系统EIRP值的降低[3],所以合理抑制噪声的低损耗波导高通滤波器成为了系统中不可或缺的重要部件。本文主要介绍了一种基于波导低频截止特性和阶梯阻抗变换的波导低损耗高通滤波器的设计方法。
1 矩形波导的低频截止特性
消失波[4]又称为凋落波、衰减波,是电磁波传播的一种现象,其特点是电磁波振幅沿某个空间方向按指数规律迅速下降,而且相位无变化,消失波就是截止频率以下的电磁波在金属壁波导传播的一种状态。
齐次Helmholtz方程对于分析电磁波在波导中的传播具有重要意义,对矩形波导采用分离变量法求解第二类齐次边界条件下的Helmholtz方程,波导内部电磁波沿z轴以系数为α的e-∝指数衰减,波导是截止频率为fc的高通滤波器,因此当频率低于其截止频率fc时电磁波会迅速衰减。
最终可得到TEmn模的截止频率为

这种工作在截止频率以下的波导称为截止波导,电磁波的频率低于波导的截止频率时就表现为消失波。利用截止波导中电磁波按指数衰减这一原理做成的截止衰减器可以用作衰减标准,在衰减计量测量技术中具有重要意义[5]。
根据计算得出的TE10消失模的主模磁场分量,可知在截止波导中TE10主模电场的分布情况:电力线处处与y轴平行,Ey的x向分布与传输波导一样为半个正弦函数的形状,沿z轴场强呈指数特性衰减,且场强的衰减速度取决于波导宽边尺寸a和电磁波频率f。
2 阶梯阻抗变换器
在两个特性阻抗不同的传输线之间插入一段或多段不同特性阻抗的传输线,适当选取其长度、特性阻抗的值和节数,便可在一定带宽内使驻波比小于一定值[6]。最简单的阶梯式阻抗变换器是一段长度为λ/4的阻抗变换器[7],如图1所示,若原有两个传输线的特性阻抗分别为Z0和ZL,则由传输线理论可知,变换段的特性阻抗为


图1 阻抗变换器示意图
这种阻抗变换器结构简单,在各种微带线和波导电路中大量应用。微带线的λ/4阻抗变换器是保持变换段的导体带与接地面之间的距离、介质特性不变,通过改变导体带的宽度来实现阻抗变换。当应用于波导时,由于波导是具有色散特性的传输线,一般需要确定矩形波导在TE10模式工作情况下的λ/4阻抗变换器尺寸。此时等效阻抗的定义有多种,但无论何种定义均有如下关系
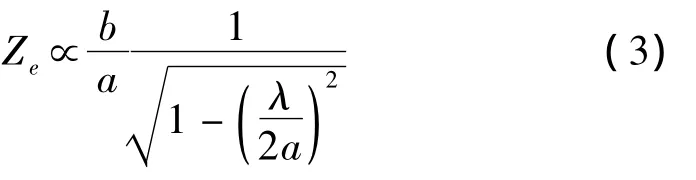
式中,a和b分别是波导宽边和窄边的长度;λ为工作波长;Ze为等效阻抗。
由式(3)可见,Ze不仅与b/a有关,还与波长有关。因此两段波导即使尺寸比相同,对于不同的λ两者的等效阻抗也不相等。只有当两段波导的宽边尺寸相等时,其等效阻抗之比才等于两者窄边尺寸的比值,且与频率无关,可认为是单纯的阻抗变换。根据λ/4阻抗变换器的计算公式可知,图1中变换段窄边的尺寸为

一阶λ/4阻抗变换器只在其工作中心频率附近的有限带宽内满足一定的匹配要求,当频率偏离其中心频率较大时其匹配性能就会下降。要拓展工作带宽就必须采用多节λ/4传输线来实现更宽频率范围内的阻抗匹配。根据λ/4阻抗变换器阻抗匹配计算公式,可得出采用两节λ/4波导进行阻抗匹配时,各节波导的窄边尺寸

从理论上讲,阻抗变换器的阶数越多,其工作带宽越宽,但阶数的增加必然导致电路尺寸增大,且带来更大的插入损耗,所以在设计时要综合考虑这些因素选择适当的阶数。
3 矩形波导高通滤波器的设计
HFSS是Ansys公司推出的专业三维电磁场仿真软件,其求解器主要采用了全波有限元法,此方法基于计算电磁学数值分析方法中的频域微分方程技术,且该软件具有较高的仿真精度和可靠性,现在已经是国际上解决计算电磁学问题的主流应用软件之一。
下面以通带为25~28 GHz、阻带为22~23 GHz、抑制度为40 dB的高通滤波器为例来介绍其设计方法。根据上述矩形波导的低频截止特性和矩形波导的阻抗变换的原理,在HFSS软件中初步建立矩形波导高通滤波器的模型,如图2所示。

图2 矩形波导高通滤波器在HFSS中的模型
一般情况下,初步建立模型的仿真结果难以达到设计要求,所以需用HFSS软件自带的优化功能对模型各参数进行优化仿真。根据之前的理论分析,该模型中的关键变量有5个,依次是高通滤波器的宽边尺寸为a1、a2,变形矩形波导的高度为b1、b2和阶梯变换的长度l;其中a1和a2决定了高通滤波器的截止频率,也是设计高通滤波器时最重要的两个尺寸,b1、b2和l可实现变形矩形波导和标准矩形波导之间的匹配过渡。
因为加工精度问题,实际加工出的滤波器与理想的模型多少存在一定差异,优化仿真后的滤波器还不能直接进行加工。接下来需要通过软件仿真的方式来验证优化设计出的滤波器是否能直接加工生产,该过程可通过软件中参数扫描功能,根据实际加工的误差大小或根据经验来调整其中的变量大小来验证设计的可行性,下面通过一组参数扫描来说明仿真设计方法。
使用软件的参数扫描功能调整滤波器的宽边尺寸得出,如图3所示的参数扫描仿真结果。
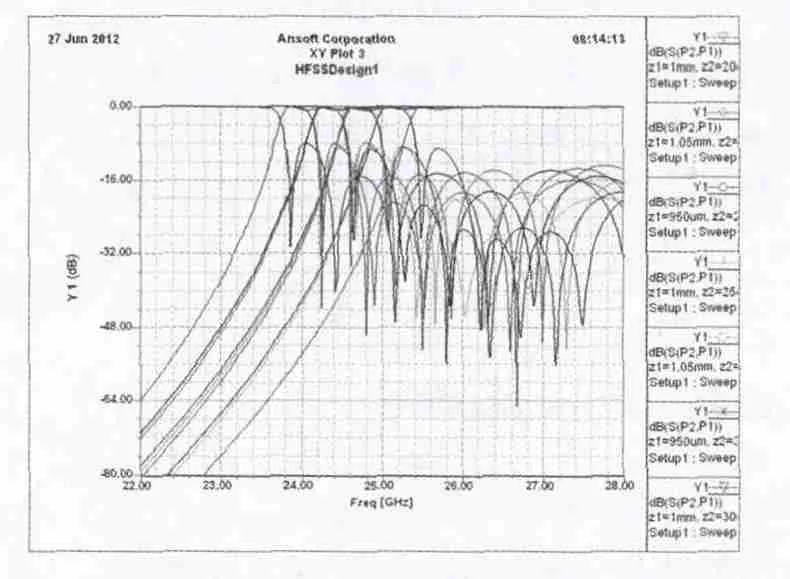
图3 矩形波导高通滤波器宽边参数扫描仿真结果
由仿真结果可看出,高通滤波器宽边尺寸直接决定了滤波器的截止点,与理论分析一致。高通滤波器窄边尺寸和过渡波导的长度影响标准矩形波导和变形矩形波导之间的匹配,合适的匹配过渡可以改善通带内的驻波,仿真结果如图4,图5所示。
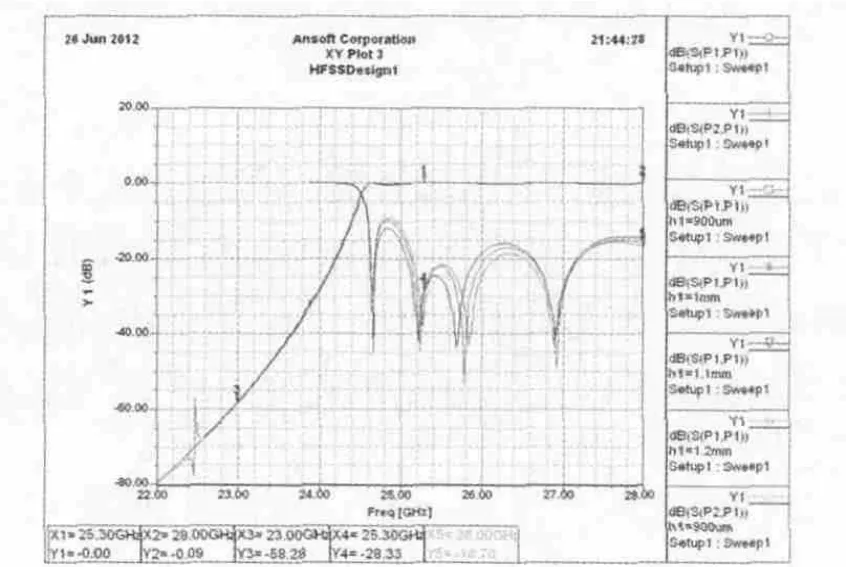
图4 矩形波导高通滤波器窄边参数扫描仿真结果
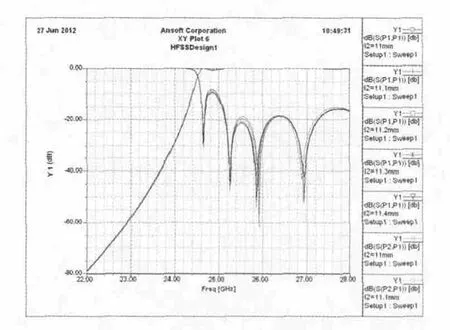
图5 矩形波导高通滤波器过渡波导长度参数扫描仿真结果
4 高通滤波器的测试
根据优化仿真和参数扫描仿真结果,择优确定高通滤波器的尺寸,该设计的高通滤波器的三维结构模型和实物照片如图6所示。

图6 波导高通滤波器三维结构模型和实物照片
利用矢量网络分析仪对高通滤波器的实物进行测试,实际测试结果如图7所示,其通带25~28 GHz,插入损耗<0.4 dB;阻带22~23 GHz,抑制>40 dB。从实测结果和仿真结果的一致性可知,该设计满足指标要求。
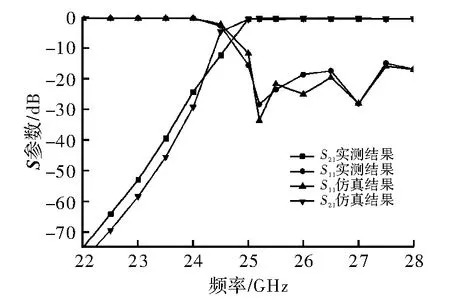
图7 波导高通滤波器实测结果和仿真结果的比较
5 结束语
通过分析及对实物的测试,证明该高通滤波器的设计方法简洁、有效、准确,在通过参数扫描等方式进一步验证后,还能进一步提高产品设计的一次成功率,可有效地指导工程研发过程。
[1]王秉钧,王少勇.卫星通信系统[M].北京:机械工业出版社,2004.
[2]郑晓天,李集林,刘海客,等.Ka频段多点波束卫星通信系统发展趋势分析[J].卫星与网络,2014(7):46-49
[3]肖永伟.Ku频段USAT“动中通”系统设计探讨[J].无线电通信技术,2011,37(2):4 -6,38.
[4]董金明,林萍实.微波技术[M].北京:机械工业出版社,2003.
[5]黄志洵,曲敏.微波衰减测量技术的进展[J].中国传媒大学学报:自然科学版,2010(1):1 -11,30.
[6]孙文武.Ka波段大功率放大器的设计[D].南京:南京理工大学,2008.
[7]高建平,张芝贤.电波传播[M].西安:西北工业大学出版社,2002.
