互通立交桥施工的交通组织优化研究
2015-12-20河北省高速公路京秦管理处河北秦皇岛066001
张 乾 (河北省高速公路京秦管理处,河北 秦皇岛066001)
ZHANG Qian (Beijing-Qinhuangdao Expressway Management Office in Hebei Province, Qinhuangdao 066001, China)
0 引 言
由交通部统计资料可知,互通式立交设计是否合理直接关系到公路的使用效率、安全程度、行车车速、运营费用和通行能力等[1];尤其是大型互通立交桥对我国经济发展具有重要意义,可以称为生命线工程[2]。但是在立交桥建设过程中传统的施工方法常常因工程占用对向车道,导致行车变窄,造成了拥堵、环境污染,以及安全事故等一系列问题[3],为此本着“边通车、边施工”的原则[4],提出了一种全新的施工组织方案,该方案不仅有效地缓解了交通拥堵,还减少了因拥堵所带来的环境污染,降低了因工程变道带来事故发生率,因此开展立交桥施工的交通组织优化研究具有重要的理论和实践意义。
1 施工方法优化
1.1 匝道的曲线要素
以某双向六车道立交桥施工区为例,跨线桥与被交路呈直角相交,则转角α=90°,单车道宽度为3.75m,主线设计速度为120km/h,右转匝道为单车道,设计速度为40km/h,对应最小圆曲线半径为60m,回旋线最小长度为35m。根据平曲线要素计算公式,计算右转匝道各个参数如下:缓和曲线长度为40m,内移值▽R为1.11m,总切线长为134.2m。根据计算结果,绘制图形如图1 所示。
1.2 施工优化方案对比
对于立交桥的建设,传统的工艺为由先修建施工便道,在修立交主体结构,在主体修筑完成后,再修筑立交匝道,整个工程结束后再挖处施工便道;新的施工工艺为,先修建匝道路基和基层,利用匝道作为施工便道,修立交主体结构,在主体修筑完成后,对施工便道(匝道) 进行面层施工即可。具体方案如图2 所示。
2 VISSM 仿真分析
2.1 方案的筛选

图2 新施工组织设计方案
新施工组织设计方案:第一种连接方式,圆曲线长度一定,半径过大时,使该连接段到被交高速之间的曲线变短,进而增大了坡度,增加了车辆爬坡困难,不利于行车安全。经过计算,当车速为35km/h 时,对应的圆曲线半径为50m,纵坡过大,达到了6.2%。因此,对于第一种连接方式,筛选出圆曲线半径为35m 和40m 所对应的两种方案共六种组合形式进行仿真分析。
第二种连接方式,将两路段进行连接,采用回头曲线的形式,圆曲线段的长度应大于半圆,这样设计的路线才会合理。但是,当设计速度为50km/h 时,圆曲线最小半径为100m,则圆曲线的最小长度为400m。与右转匝道的长度相比,一是长度过长,增加了车辆的行驶路程;另一方面,过长的中间段与右转匝道的设计量不成比例。因此,对于第二种连接方式,筛选出六种方案所对应的十八种组合形式进行仿真分析。
2.2 参数的设置
以匝道设计车速为35km/h 方案为例,进行仿真参数的设置。由前期调查数据可知,设置仿真施工区的大车比例为20%,期望车速为35km/h,跟车模型采用符合高速公路驾驶行为的Widemann99 模型;施工区路段200m,按规定据施工区200m 处设置60km/h 限速标志,匝道入口处设置相应减速标志;单车道匝道的设计通行能力一般为800~1 000 辆/h,考虑道路的实际通行能力和交通行为,交通量输入为1 200 辆/h;在整条路段起终点创建行程时间检测,路程时间检测器设置在上游匝道入口处—下游匝道出口处;仿真模型中上游路段至匝道入口450m,车辆检测器设置在下游匝道出口处,仿真时间为10min。
2.3 数据整理与分析
经过对优化方案的第一种、第二种连接方式共二十四种形式仿真计算,得到评价数据如表1 所示。
由表1 数据进行分析得到,不同匝道设计速度,不同圆曲线半径和缓和曲线组合下的形成时间和延误图如图3~4、图5~6、图7~8 所示。
(1) 第一种连接方式。由图3、图4 可知,在匝道设计速度为35km/h 的情况下,半径为35m 和40m 时,所对应的最小平均行程时间分别为23.50s 和23.43s,最小延误均为0.1s。在匝道设计速度为35km/h 的情况下,半径为40m,缓和曲线长度取25m 时,具有最小平均行程时间23.43 和最小延误0.1s。
(2) 第二种连接方式。由图5、图6 可知,当匝道设计速度为35km/h 时,半径为35m、40m 和50m 时,所对应的最小平均行程时间分别为28.98s、28.78s、35.33s,最小延误均为0.4s。总体分析,当平均行程时间及延误为半径取40m,缓和曲线长度取30m 时,具有最小平均行程时间28.78s 和最小延误0.4s。
由图7、图8 可知,当匝道设计速度为40km/h 时,半径为50m、60m 和70m 时,所对应的最小平均行程时间分别为30.38s、33.43s、35.25s,最小延误分别为0.3s。总体分析,当平均行程时间及延误为半径取50m,缓和曲线长度取25m 时,具有最小平均行程时间30.38s 和最小延误0.3s。
2.4 计算结果分析
综合考虑以上三种连接情况及不同半径、缓和曲线长度的组合,行程时间及延误所对应的最佳组合形式如表2 所示。
取三种最优组合形式,分别测试10min 内,在该组合形式下的平均行程时间、平均延误以及实际交通量,得到仿真计算最佳结果值如表3 所示。
将三种最优情况下的平均行程时间、延误时间减去原先的时间再除以原先的时间得到图9、图10。
由图9、图10 可知:平均时间缩短率最高的是第一种35km/h 最优方案;延误时间缩短率最高的是第二种35km/h 最优方案;采用综合评价法对三种方案进行评价,得到三种方案的权重分别为0.3021、0.3827、0.3152,因此,得到的结果是匝道设计速度为35km/h 的第二种连接方式最佳,其次为匝道设计速度为40km/h 的第二种连接方式,最差为第一种连接方式。
3 结束语
互通立交施工期交通组织结合主线、立交自身的改扩建方案以及施工路段的交通量情况,坚持“边通车、边

表1 仿真计算的数据表

图3 缓和曲线长度与行程时间关系图

图4 缓和曲线长度与延误关系图
图3 缓和曲线长度与行程时间关系图施工”的原则,以缓解因施工占道而产生的拥堵,保证社会的车辆正常通行提出了一种新的立交桥施工组织设计,并利用Vissm 仿真技术进行仿真分析,对设计方案进行了优化,得到了最佳的设计参数,不仅减少了建设成本和污染的排放、降低了能耗,提高了行车安全性,而且为完善公路工程技术规范提供了理论依据。

图5 缓和曲线长度与行程时间关系图

图7 缓和曲线长度与行程时间关系图
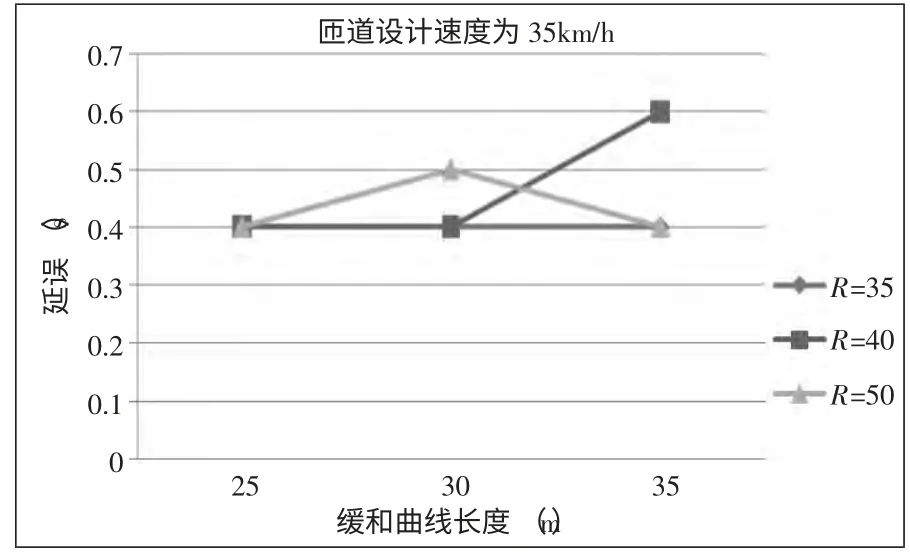
图6 缓和曲线长度与延误关系图

图8 缓和曲线长度与延误关系图

表2 仿真计算最佳连接形式表

表3 仿真计算最佳结果值
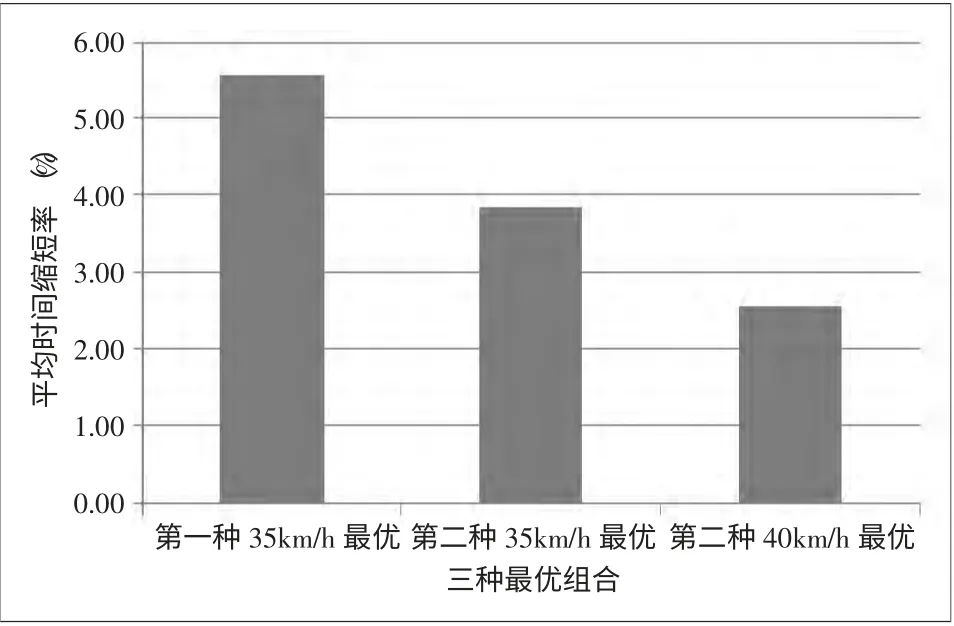
图9 平均行程时间缩短率比较图

图10 延误时间缩短率比较图
[1] 杨智勇. 互通式立交设计探讨[J]. 中南公路工程,2005(2):21-24.
[2] 孙凌. 基于普定某互通立交桥的施工技术研究[J]. 价值工程,2012(11):124-125.
[3] 雷伟. 对互通立交设计的几点见解[J]. 交通标准化,2006(8):164-166.
[4] 彭磊. 高速公路互通式立交改扩建施工交通组织设计分析[J]. 山东交通科技,2015(2):52-55.
