基于负载最近邻偏好分配的复杂网络连锁效应

段东立

（西安武警工程大学装备工程学院，西安710008）

0 引言

连锁故障普遍发生在各种关键生命线系统网络中，大规模的连锁故障一旦发生，往往具有极强的破坏力和影响力［1－2］，例如2008年初中国南方电力网络的崩溃、北美电力网大崩溃事故、因特网阻塞、2012年印度电网的两次崩溃事故以及2013年青岛输油管线的爆炸等都可以从某种程度上认为是因连锁故障所导致的灾难，这些灾难造成的损失常常十分巨大。因此，网络连锁故障理论的研究非常重要且具有现实意义。

过载机制的复杂网络连锁故障模型主要包括3个因素：负载模型、容量模型与负载重分策略［3－8］，其中负载重分策略是关键［4］。2002年，Motter与Lai［5］将过载机制连锁故障引入复杂网络的研究，提出了ML模型，假设每个节点的容量正比于其初始负载，之后，Wang和Kim［9］在该模型基础上，提出为初始负载较高的节点分配更多的容量，Li和Wang［10］认为节点的容量不仅与其初始负载相关，还与节点本身的能力（度）相关。这些模型的负荷分配规则为全局重新分配，主要是基于介数的概念，假设网络中所有信息的传输都是基于最短路径，且节点失效后网络负载以非连续的方式瞬时调整到适应新网络的状态（即新网络的介数为网络的更新负载），这种机制的主要特征是网络中所有节点都可以瞬时掌握网络的全局信息。而实际系统中，网络中的节点很难获取网络的全面信息，例如，在交通网、电力网和计算机网络中，节点之间网络流的耦合机制更为广泛的是最近邻耦合，交通网络中发生交通拥堵后，拥堵路口交通流只能选择其最近邻路段进行分流，Internet网络中某个关键路由器失效后，其承担的数据流只能通过邻近路由器重新路由。根据该特点，Wang和Chen［11］提出了一个基于最近邻负载重分配模型，节点失效后其负载由其最近邻承载，Wu［12］在该模型基础上考察了初始负荷强度参数与网络级联失效的关系。Wang［13－15］依据该最近邻择优重分规则提出了一个局域择优重分配负载模型，并定义节点初始负荷为节点度数的函数以及节点度数与邻居节点度数的函数。该类模型更加关注网络初始负荷的定义及其分布，便于分析网络抵御连锁故障鲁棒性与初始负荷模型的关系。但值得注意的是，该类模型通常假设初始负荷的分布参数与负荷分配的均匀性参数相等，这种假设是基于网络管理与网络设计完全匹配，在实际系统中很难完全达到，且该类模型忽略了网络管理措施（负荷分配机制）与负荷分布特征对网络鲁棒性影响的差异性。

为了扩展上述最近邻分配机制的连锁故障模型并考虑上述因素的影响，本文提出了一个基于负载最近邻偏好重分规则的复杂网络连锁故障模型。

1 负载重分配模型

过载机制连锁故障模型可定义为：节点i失效后网络中完好节点j的负载更新为F′j，判断F′j与节点容量Cj的关系，若F′j＞Cj则节点j触发新一轮的负载重分配，若F′j＜Cj则节点j在此时间步不失效，直至整个网络中所有节点的负载不超过其本身的容量，连锁故障过程结束。该过程中，节点i失效导致节点j的负载发生一次更新

假设负载增量ΔFj与失效节点的负载成正比

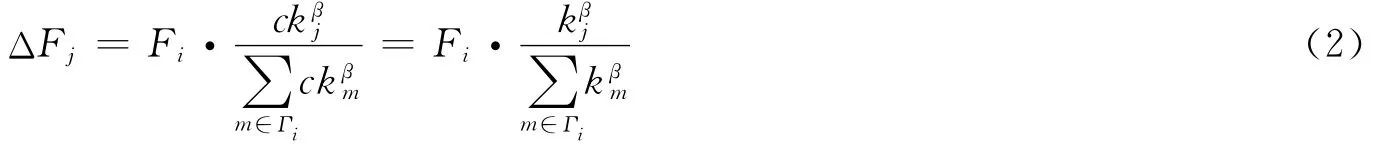
kj为节点的度数，Γi为崩溃节点i的邻居节点集合，β用来控制崩溃节点负荷的分配均匀性，且β＝0时为均匀共享负载，β＞0时重分偏好于度大的节点。节点i的初始负荷Fi与节点本身的度数ki相关，在难以确定实际负荷时可将初始负荷定义为

其中，ρ和τ为可调参数，控制节点初始负荷的强度。根据ML模型中初始负荷与节点容量的关系，将节点的容量定义为

其中，α为网络的容限系数，表示节点处理额外负荷的能力。当α足够大时，任一节点的失效都不会触发连锁故障，但是受经济与技术因素的影响，α不可能任意大，所以，可以用临界值αc表征网络抵抗连锁故障的能力。αc值越小，网络抵制连锁故障的鲁棒性越强，当α＞αc时，移除网络中的任一节点都不会触发连锁效应。为了量化整个网络的鲁棒性，也可采用失效节点的归一化指标［13，16－19］：

其中，CFi（0≤CFi≤N－1）为节点i失效触发连锁故障的节点个数。

2 理论分析

为避免连锁故障的发生，式（6）的条件应该被满足

分析不等式（7），网络免疫连锁故障的容量系数下界αc可以分别考虑为式（8）的几种情况。

其中，kmin和kmax分别为网络中节点的最大度和最小度。在实际网络系统的设计与管理中，我们关心的问题是采用何种网络结构、网络承载何种程度的负载以及单个故障时如何分配网络负荷，可以使得网络鲁棒性最强，即αc值最小。为探讨不同网络拓扑结构（度分布特征）对级联失效行为的影响，研究中选用了在现实世界中具有很好的普适性和代表性的两类网络作为级联失效的拓扑架构，分别是具有泊松分布特征的ER随机网络和具有幂律度分布特征的BA网络。

2.1 ER随机网络

ER随机网络是Erdö和Rényi提出的一种网络模型，模型中参数p为两个节点之间有边连接的概率，平均度〈k〉＝ Np，模型度分布较为均匀。ER网络可近似认为〈kβ＋1〉≈ 〈k〉β＋1，kmin≈1，kmax≈2〈k〉。因此，在ER随机网络中，网络的容限系数临界值可表示为

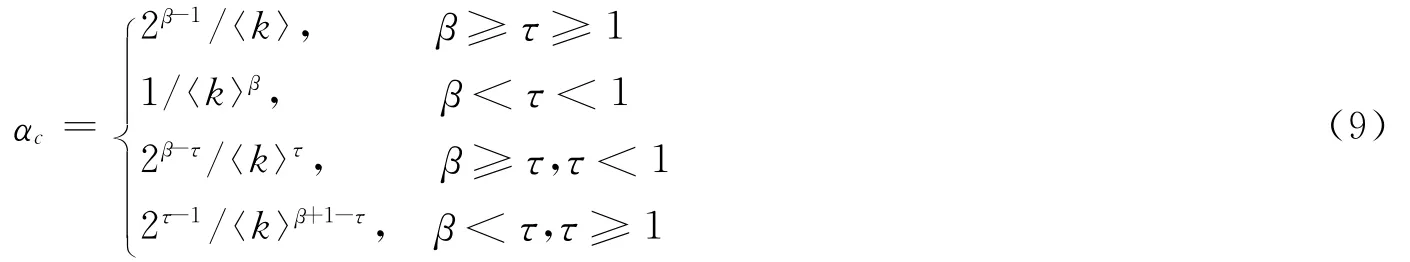
对式（9）进行简单的分析可以得出以下结论：

1）当初始负荷强度参数τ固定，β＝τ可以使得网络抵御连锁故障的鲁棒性最好。当β与τ不定时，根据式（7）使β＝τ可以得到：

当β＝τ＝1时，ER网络抵御连锁故障的容限系数临界值αc是最小的，即

2）ER网络的平均度数〈k〉＝Np越大，网络抵御连锁故障的能力越强。

2.2 BA无标度网络

BA网络是Barabási和Albert［20］提出的一个无标度网络模型，其生成机制主要为增长和优先连接。其构造算法为：1）增长：从一个具有m0个节点的网络开始，每次引入一个新的节点，并且连到m个已存在的节点上，这里m≤m0；2）优先连接：一个新节点与一个已经存在的节点i相连接的概率pi与节点i的度ki之间满足pi＝根据BA模型的演化机制，其度分布近似为。因此，

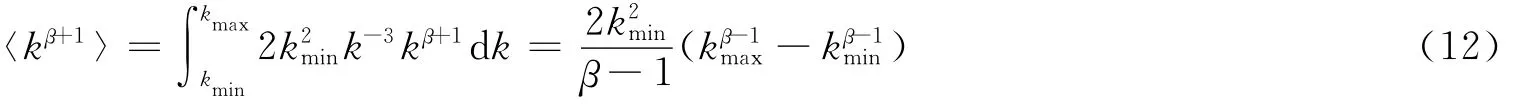
1）τ＝1时，根据BA网络的度分布，可以得到：

2）τ＞1时，

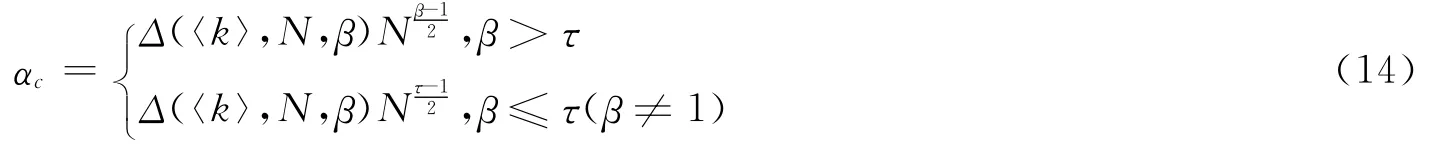
3）τ＜1时，

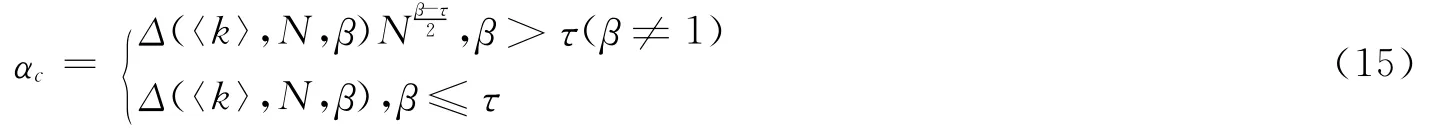
分析上述3类情形下αc随β的变化情况，BA网络在最近邻偏好重分规则下可以得出以下结论：

1）当初始负荷强度参数τ固定，β＝τ可以使得网络抵御连锁故障的鲁棒性最好。且当β＝τ时，根据式（10）可以得到

当β＝τ＝1时，抵御网络上连锁故障的容限系数临界值αc是最小的，即

2）BA网络的平均度数越大，网络的规模越大，网络抵御连锁故障的能力越强。

图1给出了ER网络与BA网络容量系数临界值的解析结果。

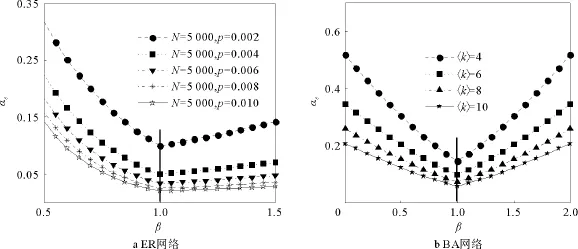
图1 容限系数临界值的解析结果（β＝τ）Fig.1 Theoretical results of capacity coefficient thresholds（β＝τ）

3 数值仿真

依据负载重分配模型分别对ER网络模型和BA网络模型进行数值仿真。图2给出了C FN指标随网络拓扑参数与容量系数变化的仿真结果。在ER随机网络中，网络规模一定的条件下，研究CFN与〈k〉（〈k〉＝Np）的关系实际上就是研究C FN 与p的关系。由图2a可以看出，ER随机网络中随着网络平均度数的增加，网络抵御连锁故障的鲁棒性逐渐增强，且在网络连接密度一定的条件下扩大网络的规模对CFN 指标基本无影响。从图2b可以看出，ER网络规模一定时，随着概率p的增大，使C FN＝0的α值逐渐减小，即相变点αc逐渐减小。BA网络中，网络规模的扩大和网络连接密度的增加都会不同程度地抑制网络连锁故障的发生。从图2c可以看出，BA网络随着网络规模与平均度数的增加，CFN逐渐减小，而且存在使得CFN＝0的相变点；从图2d可以看出，BA网络的相变点αc随着平均度数的增大逐渐减小。

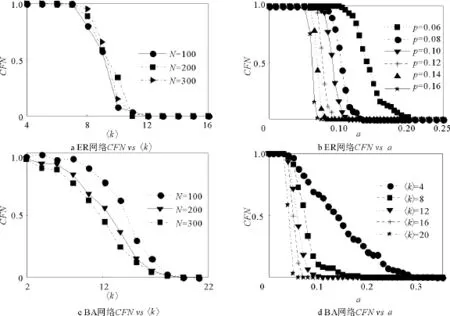
图2 ER网络与BA网络的CFN仿真结果（β＝τ＝1）Fig.2 Simulation results of CFNwith ER and BA networks（β＝τ＝1）

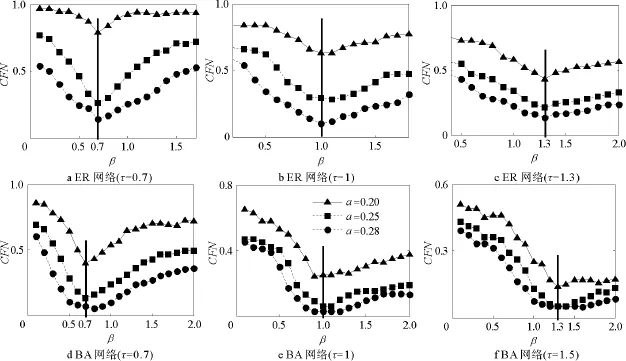
图3 ER与BA网络的CFN与负荷分配均匀性参数、负荷初始强度参数的关系Fig.3 Simulation results of CFNwithβandτfor ER and BA networks

图3给出了ER网络和BA网络CFN指标随初始负荷强度参数与负荷分配均匀性系数变化的仿真结果。设定初始负荷强度参数τ分别为0.7，1.0与1.3时，对比ER网络与BA网络不同容量系数α下的CFN，在β＝τ时，CFN取得最小值。由于网络抵御连锁故障能力的另一个度量指标容量系数临界值αc与CFN之间的关联性，很自然的一个问题是：实际网络管理中β＝τ是不是同样使得αc取得最小值？

图4分别给出了（τ＜1，τ＝1与τ＞1）3种情况下，ER网络与BA网络αc的解析结果与仿真结果。可以看出数值模拟较好地验证了解析分析的结果。也证明了β＝τ可以使得αc取得极小值，即在ER网络与BA网络结构中，合理地控制网络的负载量以及设计合适的负载分配规则会极大地减小网络连锁故障的风险。

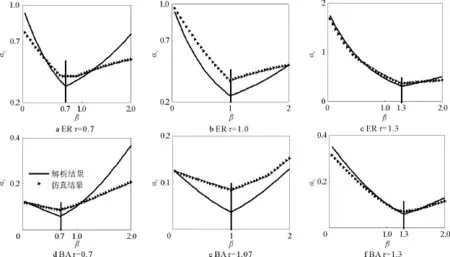
图4 τ＝0.7，1.0，1.3时，ER网络和BA网络最近邻分配规则下αc的解析结果与仿真结果Fig.4 Comparison of simulation results and analytic results ofαcwith ER and BA networks

4 结论

根据以往连锁故障模型中对初始负荷分布强度与负载分配均匀性相等的假设容易忽视这两个因素的差异性影响，本文在研究一般网络级联失效动力学行为时，假设负载偏好分配模型中初始负荷强度参数与失效节点负荷分配均匀性参数不相关，研究了ER网络和BA网络的级联失效条件，分析了网络抵御连锁故障的影响因素及其影响方式。

本文研究一方面扩展了负载最近邻偏好分配模型，便于分析现实世界中的一般网络模型，使该模型具有更普遍意义；另一方面，解析推导了ER网络和BA网络的级联失效条件，给出了网络免疫连锁故障的临界值公式，可为网络的设计和管理提供一定的指导。另外，本文的仿真结果也验证了解析分析的结论，具体到网络的设计与管理措施中，主要有以下几个基本结论：1）提高网络的连接密度与扩大网络的规模有利于抑制网络连锁故障；2）网络设计容量的增大会极大提高网络的鲁棒性，但是受成本等因素的影响，不可能无限大；3）网络初始负荷的分布与失效后节点负荷的分配规则是网络连锁故障的重要因素，在网络运行之初尽量使网络初始负荷分布强度参数与负载分配均匀性参数都在1附近可使得网络连锁故障的概率最低，在网络稳定运行时即网络负荷分布一定时，管理中尽量使负载分配均匀性参数与负荷分布强度参数一致，也可使得网络连锁故障风险最低。

需要指出的是，本文的模型和结论针对最近邻耦合机制，而实际系统运行时的动力学行为也可能是全局耦合机制或介于最近邻和全局之间的耦合机制，这种动力学机制对网络连锁故障行为也会产生不同的影响；而且，网络的失效机理不仅仅是过载机制，网络的失效行为也可能是由网络个体之间的依赖、因果、控制等关系引起。因此，更为贴近实际系统运行机制的网络动力学行为是下一步研究的重点。

［1］ Buldyrev S V，Parshani R，Paul G，et al.Catastrophic cascade of failures in interdependent networks［J］.Nature，2010，464（7291）：1025－1028.

［2］ 丁琳，张嗣瀛.复杂网络上相继故障研究综述［J］.计算机科学，2012，39（8）：8－13.Ding Lin，Zhang Siying.Survey on cascading failures on complex networks［J］.Computer Science，2012，39（8）：8－13.

［3］ Crucitti P，Latora V，Marchiori M.Model for cascading failures in complex networks［J］.Physical Review E，2004，69（4）：045104.

［4］ 段东立，吴俊，邓宏钟，等.基于可调负载重分配的复杂网络级联失效模型［J］.系统工程理论与实践，2013，33（1）：203－208.Duan Dongli，Wu Jun，Deng Hongzhong，et al.Cascading failure model of complex networks based on tunable load redistribution［J］.Systems Engineering Theory ＆Practice，2013，33（1）：203－208.

［5］ Motter A E，Lai Y C.Cascade－based attacks on complex networks［J］.Physical Review E，2002，66（6）：065102.

［6］ 王建伟.网络上的相继故障模型研究［D］.大连：大连理工大学，2010.Wang Jianwei.Study on cascading failure model on networks［D］.Dalian：Dalian University of Technology，2010.

［7］Zheng J F，Gao Z Y，Fu B B，et al.Cascading failures in congested complex networks with feedback［J］.Chinese Physics B，2009，18（11）：4754－4759.

［8］ Hu K，Hu T，Tang Y.Model for cascading failures with adaptive defense in complex networks［J］.Chinese Physics B，2010，19（8）：080206.

［9］ Wang B，Kim B J.A high－robustness and low－cost model for cascading failures［J］.Europhysics Letters，2007，78（4）：48001.

［10］Li P，Wang B H，Sun H，et al.A limited resource model of fault－tolerant capability against cascading failure of complex network［J］.The European Physical Journal B，2008，62（1）：101－104.

［11］Wang W X，Chen G R.Universal robustness characteristic of weighted networks against cascading failure［J］.Physical Review E，2008，77（2）：026101.

［12］Wu Z X，Peng G，Wang W X，et al.Cascading failure spreading on weighted heterogeneous networks［J］.Journal of Statistical Mechanics：Theory and Experiment，2008，（5）：05013.

［13］王建伟，荣莉莉.基于负荷局域择优重新分配原则的复杂网络上的相继故障［J］.物理学报，2009，（6）：3714－3721.Wang Jianwei，Rong Lili.Cascading failures on complex networks based on the local preferential redistribution rule of the load［J］.Acta Physic Asinica，2009，（6）：3714－3721.

［14］王建伟，荣莉莉.面向相继故障的复杂网络上袭击策略研究［J］.中国管理科学，2009，（1）：125－130.Wang Jianwei，Rong Lili.Cascade－oriented attack on complex networks［J］.Chinese Journal of Management Science，2009，（1）：125－130.

［15］王建伟，荣莉莉.基于袭击的复杂网络上的全局相继故障 ［J］.管理科学，2009，（3）：113－120.Wang Jianwei，Rong Lili.Universal cascading failures on complex networks based on attacks［J］.Journal of Management Science，2009，（3）：113－120.

［16］Wang J W，Rong L L.A model for cascading failures in scale－free networks with a breakdown probability［J］.Physica A，2009，388（7）：1289－1298.

［17］Wang J W，Rong L L，Zhang L，et al.Attack vulnerability of scale－free networks due to cascading failures［J］.Physica A，2008，387（26）：6671－6678.

［18］Wang J W，Rong L L.Cascade－based attack vulnerability on the US power grid［J］.Safety Science，2009，47（10）：1332－1336.

［19］Wang J W，Rong L L.Robustness of the western United States power grid under edge attack strategies due to cascading failures［J］.Safety Science，2011，49（6）：807－812.

［20］Barabási A L，Albert R.Emergence of scaling in random networks［J］.Science，1999，286（5439）：509－512.