社会网络的层次结构发现

成 清，黄 森，黄金才

（1.国防科学技术大学信息系统工程重点实验室，长沙410073；2.78020部队 昆明650221）

0 引言

现实生活中很多自然、社会系统都可以用复杂网络来描述，如社会网络［1－2］，Internet网络［3－4］，和生物网络［5－6］等。网络通常都具有某些结构特征，如模体、模块性和层次结构等。其中网络的层次结构是一种最为常见的组织结构特征，如军事组织、企业组织等都具有典型的层次结构特征。分析网络的层次结构不仅有助于揭示网络自身组织结构与形成机制，使人们更好地理解系统不同层次的结构和功能特性，而且对自然网络和人工网络的认识和干预有重要意义，是了解人类行为模式的基础。目前对网络层次化结构挖掘的研究主要从如下几个方面进行：

层次结构就是网络中节点按照某些值的排序［7］，认为整个网络具有k层，综合节点自身属性或拓扑特征，建立所有节点层次测度指标，计算它们的指标值，将其映射到k层中的某一层，主要有中心性计算方法［8］，k－core测度计算方法［9］和层次指标度量方法［10］等和影响力对比方法。

层次结构是一种嵌套层次［11］，高的层次包含低的层次。主要有层次聚类方法［12－14］，主要思想是把网络中的节点或边作为聚类单元，选择相似性最大的聚类单元进行聚类，得到一些规模比较小的社区，再对这些小社区进行聚类，得到一个大一些的社区，如此聚类，形成一颗树状图，即网络的层次结构。

以树结构作为层次结构［15］，如结构匹配方法，此类方法用树结构来代替层次结构，然后再利用已知信息，生成符合该特征的备选树，最后再选择最优匹配结构为该网络的层次结构。

上述研究大都没有深入分析现存网络中层次结构的特征，也未仔细分析网络内部信息的交互过程。针对此问题，最新的研究提出层次结构是一种流层次结构，并且节点排序和嵌套层次结构都能转换成流层次结构［16］。流层次结构首先是基于节点对整个网络的影响排序，然后根据排序高节点到其它节点的局部可达集中性来确定层次结构。但这种方法是基于传统的社会网络图模型的，没有考虑到社会网络现实的固有属性特征，比如一个公司成员的职位高低，两个人之间朋友关系的亲疏等等；另外，流层次结构并未确定流的最佳路径，即不能挖掘出网络的骨干层次关系。针对上述问题，本文考虑节点和边的固有属性建立社会网络扩展图模型，然后在流层次思想的基础上，定义了面向使命任务的层次结构，并提出基于信息粒子流动的层次结构发现方法。

1 社会网络的扩展图模型

在实际网络中，大部分的节点与节点都存在差异性，且节点之间的连接程度也有所不同。造成这些差异的原因是节点或边之间的属性不同。因此，本文考虑节点和边的属性，建立扩展图模型G＝（V，E，δ，μ），其中V为节点集；E为边集；δ是从点集到［0，1］的映射，代表节点的综合属性值；μ是边集到［0，1］的映射，代表节点与节点的综合关系属性。

1.1 节点的抽象

对节点的抽象实际上就是将节点的相关属性映射到节点的综合属性上，即确定G中的δ，其数学描述为：假设节点的属性向量FV＝｛fv1，fv2，…，fvn｝为自变量，综合属性δ为因变量，则需建立一个δ＝f（FV）∈［0，1］的函数映射关系［17］。本节从节点属性的分布出发，通过投影的方法，将节点的属性向量FV＝｛fv1，fv2，…，fvn｝，映射到投影特征值z上，由此得到δ＝f（z）。最后，再将节点的综合属性映射到［0，1］空间中，即δ→［0，1］。具体过程如下：

首先，进行属性的归一化，在实际问题中，影响节点重要程度的属性很多，其量纲和取值范围也可能有很大的差异，为有取值的属性去量纲化和数据归一化，把属性数据都变化到［0，1］区间上。

然后，把属性向量FV＝｛fv1，fv2，…，fvn｝综合成a＝｛a1，a2，…，an｝为投影方向的一维值zi，即

投影方向实际上反映了各个属性值对于重要程度的权重。如果有充分的先验信息或者知识，那么就可以为投影方向的确定提供支持，如AHP方法；如果没有足够的先验信息来提供支持，则可以根据属性的分布和具体应用采用投影寻踪［18］的方法确定其投影方向。

最后，将投影值进行伸缩变化，将节点的综合属性映射到［0，1］空间中。如采用δi＝zi／zmax。其中，zmax是最大的投影值，zi是某一节点的投影值。

1.2 关系的抽象

社会网络的扩展图模型中定义节点间的关系如下：在一个有限的节点集合V中，关系可以定义为μ：V×V→［0，1］，表示为

其中，记rij：＝μ（vi，vj），矩阵R＝（rij）n×n为关系的邻接矩阵，采用关系的重要性代替关系的存在性，针对特定的社会事件恰当地抽象出它的重要性，并赋予［0，1］之间的相应的权值，来度量社会关系在社会网络中的表征。

另外，对于某一对相邻节点而言，可能发生多次社会事件，本文引入文献［19］中提出的聚合操作来处理多重关系的聚合问题。当图G中出现平行边，即某对相邻节点具有多个关系时，定义聚合操作用来对多个关系进行聚合，若α和β为G中某相邻节点的两个社会关系，则α⊕β＝α＋β－αβ。

可见拓展图实际上是在传统图的基础上增加了节点和边的权重，但是节点和边的权重并不像传统图一样是单一属性的度量，而是采用节点属性投影和多个关系的聚合操作实现多属性的综合映射，模型能够更好地考虑节点和关系的多属性特征。虽然由于进行了投影操作，增加了计算复杂度，但投影计算只用在网络构建中，当网络构建后不会影响到网络的分析。

2 网络的层次结构定义

一个复杂的组织应对具体任务时，它自适应地表现出来的一种层次结构，任务指派是通过节点间的信息流动实现的。面对不同的任务使命时，任务的指派是不同的，所以信息流也是不同的，相应的层次结构也是不同的，这同文献［16］中认为层次结构是一种流层次结构的思想相似。

指定给组织的使命任务可分解成一组基本任务，称为任务空间［20］，任务空间中的每一个任务都会被分配给组织中的某个组织成员负责或控制，我们称这个组织成员为主控成员。在任务空间从顶层到底层的粒化过程中，每生成一个子任务，都会为相应的子任务指定一个主控成员。实际上就是任务树的生成过程，由此，可以获得相应的主控成员树，如图1所示。

层次结构就是由主控成员与每个主控成员所属的普通成员构成。从任务流角度看，即确定使命任务的主控成员｛S｝，即根节点，和能具体执行任务的普通成员｛T｝，即叶节点，它们之间存在任务指派流，层次结构的存在，就是为任务指派信息的流通提供一种信道，因为考虑的是连通图，因此它们之间一定存在一条最优信道（最优信道即在最短时间内能够通过最多信息量的信道），记为r（·，·），如r（a，b）表示从节点a到节点b的最优信道，最优信道上的节点就位于相应的层次上，如r（a，b）＝（a＝u1，…ui，…，b），则ui位于第i层，当然一个节点可能位于多个层次上，因为这个节点可能位于多条最优信道上。所以层次结构为Г＝∪r（si，tj），其中si∈ ｛S｝，tj∈ ｛T｝。如果把信道看作路径的话，从根节点到叶节点的最优路径可能不止一条，造成层次结构的不唯一。因此，本文把最优信道也可看作是一个子图，该子图是从根节点到叶节点的连接子图，旨在能从根节点携带最多的信息粒子到达各个叶节点。如图2所示，根节点为A，它是使命任务的总控成员，H，J，K，L是叶节点。那么根节点A通过信道把信息传递给叶节点 H，J，K，L，假设把路径长度作为最优信道的度量，可分别得到r（A，H）＝ （A，B，D，H），r（A，I）＝（A，B，D，E，I），r（A，J）＝ （A，B，E，F，J），r（A，K）＝ （A，C，F，G，K）和r（A，L）＝ （A，C，F，G，L）5条信道或子图，将这5个信道的点集和边集做并操作，得到一个新的集合，很显然这就是需要挖掘的层次结构，也是骨干层次关系。

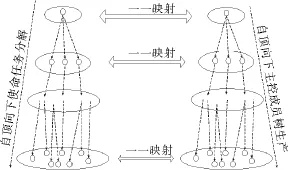
图1 主控成员树生成图Fig.1 Spanning graph of the master tree

图2 简单的层次结构示意Fig.2 The schematic diagram of the hierarchical structure

3 网络的层次结构发现方法

根据所定义的层次结构，我们分两步对层次结构进行挖掘：首先挖掘出根节点和叶节点（根节点和叶节点下文称骨架点）；然后再挖掘出它们之间的信息流通信道，即层次结构。

3.1 骨架点的挖掘

根据数据场理论，针对给定网络G＝（V，E，δ，μ），网络中节点表示数据场中的数据对象，每个节点周围存在一个作用场，位于场中的任何节点都将受到其它节点的联合作用，根据真实网络的特性，我们认为，节点间的相互作用具有局域特性，每个节点的影响能力会随着网络距离的增长而快速衰退，采用短程场且具有良好数学性质的高斯势函数描述节点间的相互作用［21］，综合考虑网络拓扑性质和节点固有属性，可以得到任意节点vi∈V的拓扑势可表示为

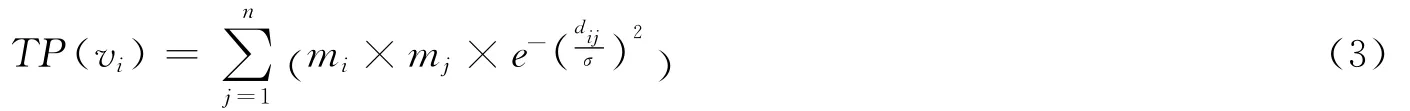
其中，dij为节点vi与vj间的拓扑距离；影响因子σ表示节点的作用范围；mi≥0表示节点vi（i＝1，2，…，n）的质量。

相比较传统的社会网络而言，社会网络扩展图最大的不同就在于它的每一个节点和每一组关系都是一个综合属性值。本文以节点的综合属性值作为其节点质量的度量。联系的属性值来源于对引发联系的社会事件的抽象，代表其强弱程度。在扩展图中，关于点到点之间的路径的选择采用基于边的综合关系属性值映射的距离定义，即d：E→R＋，R＋＝［0，＋∞），对于任意e∈E，称d（e）为枝e的长度，设P＝ue1v1…vk－1ekv是G中连接u与v的路，称为路P的长度。

在G中，有μ：E→［0，1］是从边集到［0，1］的映射。因此，必须设计一种综合关系属性值到距离值的函数映射d：E→R＋，它满足条件：

1）定义域为［0，1］，而值域为［0，＋∞）；

2）d（μ（e））＝0，当且仅当μ（e）＝1；

3）当μ（e）→0时，d（μ（e））→＋∞；

4）d（μ（e））在定义域上是单调递减、连续光滑的函数。

本文使用函数d（x）来实现这个映射，即

可得

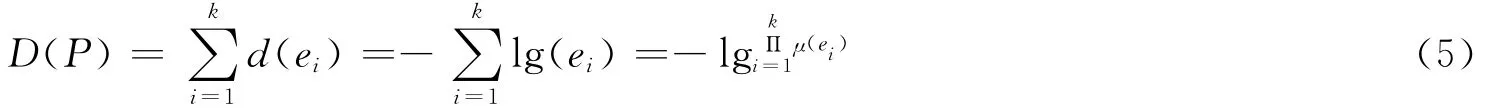
当存在路径P＊，使得D（P＊）≤D（P），那么P＊就是两点之间的最短路。显然从式（5）可知，这条路上全部枝的综合关系属性值的乘积，是所有路径上全部枝的综合关系属性值的乘积的最大值。

另外存在一个参数，影响因子σ，根据数据场中关于影响因子的讨论［21］，可以引入拓扑势场的势熵来衡量σ值的合理性，令节点v1，v2，…，vn的势值为TP（1），TP（2），…，TP（n），则势熵可定义为

在一个社会网络中，如果将节点u断开，与之相关的联系也认为失效，就会导致网络结构的变化，这种变化就会让另一个节点v的重要性发生变化，这种现象叫做v在某种程度上依赖于u，反过来看，便是u在某种程度上支持v。这种现象反映了节点在网络中的一种社会性，表现一个节点对另一个节点重要性的支持。在对节点拓扑势的计算中，已经包含了这种思想，因为拓扑势的形成，就是由其他节点的能量辐射造成的，这种能量的辐射也是给力的一种表现形式，所以本文将某一节点对另一节点拓扑势的支持程度，叫做势支持，则有φG（vi）为节点vi在网络G中的拓扑势，又vi，vj∈V，那么vi对vj的势支持Supp（vj→vi）为

其中，G－vj表示在图G中去掉节点vj之后的子图，φG－vj（vi）表示在图G－vj中节点vi的拓扑势。势支持的思想可以从描述两点之间的关系，推广到整个网络上，定义某个节点对整个网络的势支持。先定义网络的拓扑势为

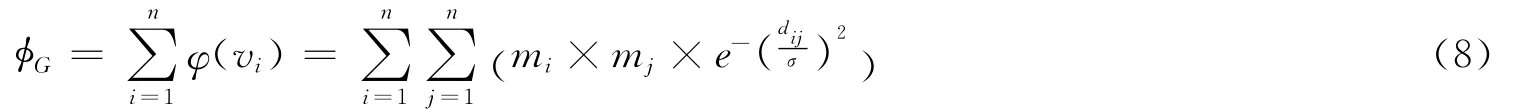
由此，定义节点vj对整个网络的势支持为

节点势支持的应用意义在于，它主要描述的是某一节点所拥有的能量在多大程度上依赖于另一节点的存在。网络势支持主要描述的是整个网络的能量在多大程度上依赖于某一节点的存在。

从结构意义上来看，根节点只有出度没有入度，也就是说，它主要根据自身的属性和能量对下层的节点进行支持，而被支持的节点对其依赖程度是很大的。叶节点只有入度没有出度，也就是说它不再支持别的节点，而主要是被支持。

从信息流动的角度，根节点对使命任务、外部环境和整个网络组织都具有较为全面的信息了解，所以它主要是进行任务信息的初始发送，对整个网络的信息提供支持。而叶结点可能只需掌握自身的子任务与之相关的信息，所以它是信息流动的汇，所有的任务信息最终都流向这些叶节点。

可见不管是从结构意义、信息流动，还是从实际的物理意义而言，根节点对整个网络结构都应该具有最大的势支持，而叶节点则对整个网络结构具有最小的势支持，因为它基本属于完全被支持的地位。

3.2 层次结构的发现

根据节点对网络的势支持确定根节点和叶节点之后，需要挖掘根节点和叶节点之间的流通信道。根据层次结构的定义，流通信道是一个从根节点到叶节点的连接子图，旨在从根节点携带最多的信息粒子到达各个叶节点。因此，流通信道的挖掘问题归结为根节点分别与不同叶节点之间的最优子图挖掘。

该问题描述为：对于给定图G＝ （V，E，δ，μ），两个节点s和t，s，t∈V 且s≠t，s为根节点，t为叶节点。定义一个子图质量函数f（·），找到一个包含s和t的连通子图C，使得f（C）最大。所以首先需要确定图质量函数。受文献［22］的启发，本文引入电流网络的计算方法来分析信息粒子在根节点和叶节点之间的流动过程。通过使用模拟信息粒子的随机游走过程，使得最优子图中能在s和t中运送最多粒子，这些粒子是一直都在该子图中，并且最优子图包含的节点最少。由此提出最优子图的挖掘方法。

在粒子流与电子流的类比分析中，如果将1V的电压加在节点s和t之间，V（s）＝1，V（t）＝0，则任何一点的电压则可以理解为粒子从该点出发，到达t点之前到达s点的概率；而电流则可以理解为1A的电子流从s出发流到t被其吸收，而流过边的电流的大小表示粒子在游走期间，通过该边的概率值。因此可以假设I（u，v）便是从节点u到节点v的电流，U（u）为节点u处的电势，那么根据欧姆定律，在同一电路中，导体中的电流跟导体两端的电压成正比，跟导体的电阻阻值成反比，可以得到：

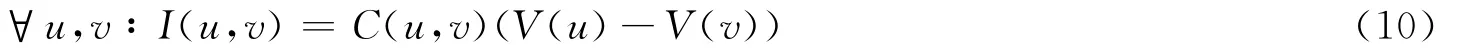
其中，C（u，v）为节点u和v之间的电导系数，在本文中C（u，v）＝μ（u，v），μ（u，v）表示节点u和v的综合关系属性值。

另根据基尔霍夫电流定律的描述，流入一个节点的电流总和，等于流出节点的电流总和，可以得到：

所以，根据欧姆定律和基尔霍夫电流定律，可以得到计算这个网络中所有节点处的电势就可以转化为求解如下一个线性系统：

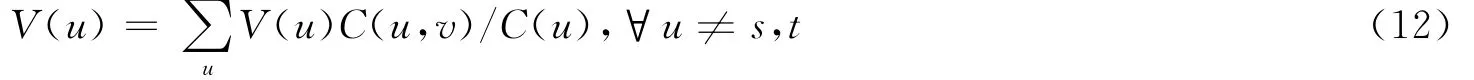
这种方法与粒子在图上的随机游走过程本质是一样的，假设s是发射态，t是吸收态，则可能存在s1到t1和s2到t2的最优路径，有P1＝s1a1t1且P2＝s2a2t2，认为两条路径完全一样。事实上，应该对度高的节点采取一种惩罚措施，因此引入沉没点z的概念，与t一样，它也处于吸收态，一旦粒子到达这一点，它就不再游走，所以V（z）＝0，并且设定与沉没点连接的那条边的电导系数为［22］

因此，粒子流不一定全部都由s出发流向t，它有一部分也可能流向沉没点z，很显然，度为1的点都可以设置为沉没点，这就是对度多的点和节点多的子图的惩罚，因为度越多，粒子流向沉没点的可能性越大。电子流是从电势高的节点流向电势低的节点。如有V（u）＞V（v），则I（u，v）＞0，即电子流从u流向v，记为u→v。路径P是从s节点到ui节点，记为P＝（s，…，ui），其中对于路径中的任意j都有uj→uj＋1，由于电子流是从电势高的节点流向电势低的节点，所以路径中不存在环路。据此有

定义1［22］在路径P ＝ （s＝u1，…，ui）上，传递的电流DF（P）为

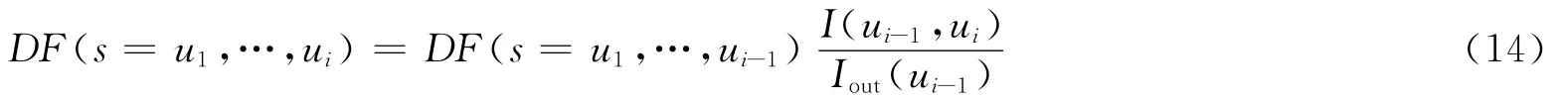
定义2［22］在原图G中的一个子图G＊，它所具有的传递电流为所包含的所有路径的传递电流之和：

如果s，t∈G＊且G＊假设为从节点s到节点t的最优子图，则对于任何一个子图G′，都有

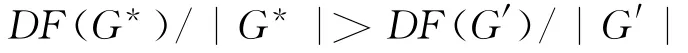
其中，｜G＊｜是G＊中所拥有的节点数。代表从s流出的信息粒子通过G＊流向t，是以最小的代价携带了最多的粒子流。所以，f（G＊）＝DF（G＊）符合最优子图质量特征的函数定义。

根据定义的图质量函数，可以采用文献［22］中的最优连接图发现算法发现最优子图。

然后根据层次结构的定义，可知层次结构是最优子图的并集，它的物理意义是，希望找到组织在信息流动层面上的骨干层次结构，所以只需动态挖掘出这些最优子图，然后将它们做并操作，就是所定义的层次结构。

综合上述，整个层次结构的挖掘过程是：设层次结构为Г（V，E），节点和边都初始化为空。首先，根据节点的网络势确定最大的势支持点s和若干最小势支持点t＝｛t1，t2，…｝；然后计算出它们之间的最优子图，如s到t1的最优子图Gsub1，然后在原图中删除最优子图除s的部分，继续找到剩下的图中势支持最小的点t2，并计算s与t2的最优子图Gsub2，删除Gsub2中除s的部分，继续重复操作，直到所有的点都被包含，最后Г（V，E）＝∪Gsubi（i≤｜V｜）。具体算法伪代码为：

4 实验分析

2002年1月2日，Enron公司宣布申请破产保护。之后，联邦能源规划委员会开始了对Enron公司的财务调查，其中一项是通过调查公司员工的邮件进行的，并于2003年10月14日将邮件系统公布在网上以视公正。最初Enron邮件语料集包含了158个用户的619 446封邮件信息，除去附件后有用户151个，邮件信息文件约517 431个，有很多研究者对Enron邮件数据做过处理，对应不同的版本，本文用到的Enron Email数据集见文献［23］。考察从1998年10月到2002年9月这47个月的邮件发送量，便可以得到每个月份的邮件发送量分布（见图3）。

另外本实验还用到另一份人名与职位的对应表和一份人名与邮箱的对应表，其中只有104个人的职位是确定的，为了使后续实验更加精细，所以我们的分析对象就是这104个人所构成的邮件通信网络。

本实验旨在研究Enron公司在应对日常业务和财务危机时的层次结构。在建模时，主要考虑的是与完成使命任务相关的属性，对于节点，主要考虑成员职位，本文把组织中的9种职位大致归为5个等级［24］（见图4）。同时也综合了成员邮件的发送量，成员邮件的接收量和成员邮件的平均回复时间3个属性，不过只对职位属性值进行差异性调整，所占比例较小。所以节点的综合属性主要反映了节点的职位等级。

图3 每个月份邮件的发送量统计图Fig.3 Distribution of sent eamils over time（month）

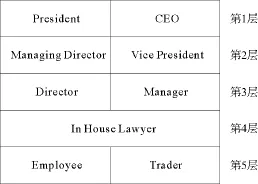
图4 职位的分层图Fig.4 Dierarchical diagram of position

对于关系，设置一个阈值2，当邮件通信量高于这个阈值时，才将这个关系抽象为一条边，而且综合邮件通信的通信频度和邮件平均回复时间计算其综合关系。

4.1 应对日常业务

我们选择发生财务危机之前半年的邮件数据作为实验的基础数据，即2001年2月到2001年7月这6个月的数据，也就是图3中显示的第1段数据。在这半年中，综合考虑节点和关系的固有属性，可以得到如图5所示的社会网络扩展图。同时，根据公式（9）可以计算节点的网络势支持（见图6）。

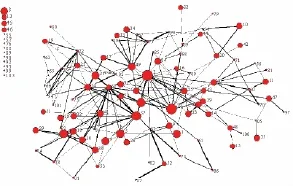
图5 应对日常业务的社会网络属性图模型Fig.5 The attribute－graph model of social network of enron＇s daily business

图6 应对日常业务的网络势支持分布图Fig.6 Distribution of network potential support for enron dealing with the daily business

由图6可知，网络势支持最大的节点为3，其次是节点68，而节点8，12，45，46，55，57，76，88，89，90，92，93，99和103的网络势支持较小，几乎为0。可以把网络势最大的节点作为根节点，如节点3，网络势支持较小的点作为叶节点，采用HierarchicalMining算法可以得到整个网络的层次结构，如图7所示。

因为节点的综合属性值基本反映了现实网络中节点的职位等级，从图7可以看出，整个挖掘出的骨干层次网络基本符合现实网络中职位的高低，即综合属性值较小的基本在综合属性值较大的下一层。但是个别综合属性小的节点却位于综合属性大的节点的上层，如节点68，现实职位虽然不高，但在应对日常业务中，它同节点3的综合关系强度较大，而且节点3到节点5，6大部分通信都频繁通过3进行，是高层之间的纽带，还有如图6，节点68对的网络势支持仅次于节点3，可见其对整个网络的影响很大，所以综合其固有属性和拓扑结构，从信息流角度分析节点68位于层次结构的高层是合理的，而且这也符合现实Enron公司中，节点68的职位虽然是职员，但是他的工作却是负责管理关系的。另外，如职位等级较高的节点19，22，35，42等节点都是位于层次结构的叶节点，是由于在现实网络中，他们本身就处于网络的边缘（见图5），所以从信息流角度认为他们在层次结构的底层。

4.2 应对财务危机

Enron公司的破产源于一次偶然的财务危机，从每个月的邮件数据库中的数据多少就可以看出，这次危机让整个公司处于超负荷运转。为了研究其应对财务危机时，公司组织的层次结构，我们选择2001年9月到2002年2月这半年的邮件数据作为应对财务危机的基础数据，也是图3中虚线显示的第2段数据。

综合这段时间节点和关系的固有属性，可得到如图8所示的社会网络扩展图。同样根据公式（9）可以计算节点的网络势支持（见图9）。由图9可知，网络势支持最大的节点为3，其次是节点85，而节点5，7，34，52，54，55，61，75，76，80，81，86和100的网络势支持几乎为0。

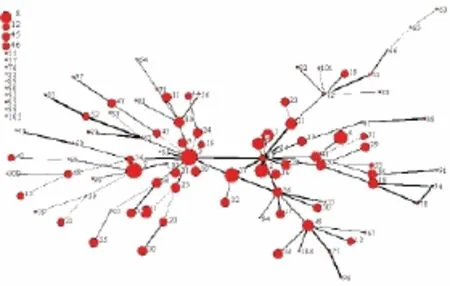
图7 应对日常业务的层次结构图Fig.7 Hierarchical graph of enron＇s daily business

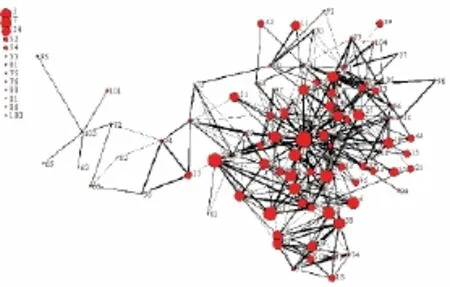
图8 应对财务危机的社会网络属性图模型Fig.8 The attribute－graph model of social network of enron＇s handing of the financial crisis

可以把网络势最大的节点作为根节点，如节点3，网络势支持较小的点作为叶节点，采用HierarchicalMining算法就可以得到整个网络的层次结构如图10所示。由图10可见整个挖掘出的骨干层次网络基本符合现实网络中职位的高低，即综合属性值较小的基本在综合属性值较大的下一层，并且呈现星型层次结构，高层之间的通信更加紧密，由图10中综合关系强度可以看出，不像在应对日常业务时频繁通过节点68进行通信，而是直接进行通信。但是在发现层次结构中，个别综合属性小的节点却位于层次结构的较高层，如节点85，现实网络中他的职位虽然是职员，但他直接位于根节点3的下层，而且他们之间的综合关系很强，这同他在应对财务危机中扮演着首席运营官的角色的现实是相符合的。另外，在现实网络中处于边缘的节点在层次结构中也处于底层，如节点11，18，42等。

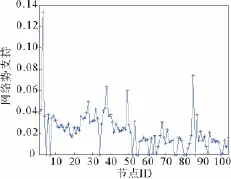
图9 应对财务危机的网络势支持分布图Fig.9 Distribution of network potential support of enron＇s handing of the financial crisis

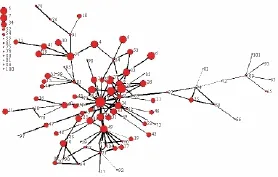
图10 应对财务危机的层次结构图Fig.10 Hierarchical graph of enron＇s handing of the financial crisis

通过对面向日常业务和财务危机两个不同的任务的层次结构发现，可以发现：

1）节点在不断更新。全时间段的社会网络包含了所有的104个成员，然而第1时间段的社会网络中没有8，12，45，46，55，57，76，88，89，90，92，93，99和103这14个节点，在第2时间段的社会网络中没有5，7，34，52，54，55，61，75，76，80，81，86和100这13个节点，其他节点均有出现和退出现象，这些现象可以在Enron公司发生的解聘和聘用事件中找到根源，比如节点8就是在第1时间段之后被公司解聘了。

2）通过图7和图10对比可知面向不同任务时，组织网络的层次结构是不同的。也验证了网络层次结构的形成依赖于具体的使命任务，面对不同使命任务时，相应的层次结构是不同的。如节点68在应对日常业务任务中为第2层中最重要的节点，其下层还连接着许多第3层节点；而在应对财务危机中，除了68外，还有85，49等第2层中比较重要的节点，可见在面向不同任务时，节点扮演的角色也不同，节点所处的层次也不同。

3）通过图7和10对比可知为了有效应对财务危机，公司的高层之间联系紧密，完全以节点3为核心，而面向日常业务时层次结构相对较稀疏。同时，在应对日常业务时，两相邻节点之间的平均紧密度为0.42，平均长度为0.86，根节点到各个节点的平均长度为2.22，平均紧密度为0.11，最大长度为7.59；在应对财务危机时，两相邻节点之间的平均紧密度为0.63，平均长度为0.47，根节点到各个节点的平均长度为1.22，平均紧密度为0.29，最大长度为7.02。可见在应对财务危机中顶层到底层的紧密度更高，距离更短。

4）通过层次结构的发现，精简了网络，从复杂的原始网络中挖掘出了网络的骨干关系，能够清晰地展现公司在面向不同任务时的组织模式和运作流程。同时，也有利于分析节点所扮演的不同角色，和节点的负载情况。如节点68在面对日常业务中比在面对财务危机中扮演着更重要的角色；另外，在面对财务危机中节点3的下层次节点数比日常业务中大得多，可见其在财务危机中的负载比日常业务中的大得多。

5 结语

社会网络分析由于其巨大的应用价值而成为近年来研究的热门课题之一，受到了越来越多研究人员的关注。社会网络的层次结构发现也是社会网络研究的一个重要方面。针对传统的建模手段无法刻画出真实社会网络的属性特征，本文建立了社会网络的扩展图模型。虽然此框架并未考虑所有可能的投影情况，但可以为以后对不同的社会网络进行建模起到一个借鉴的作用。在流层次结构思想基础上，认为网络的层次结构是受使命任务驱动形成的，并定义了面向使命任务的层次结构。然后，提出了基于势支持的层次结构中骨架节点的发现方法，并通过对比信息粒子的游走过程和电流网络的计算原理，引入电流网络的计算方法来分析信息粒子在骨架节点之间的流动过程，提出了基于势流动的层次结构发现方法。最后通过对Enron公司邮件数据的分析，挖掘出Enron应对日常业务和财务危机的层次结构，并阐述了其价值。但是本文虽然对网络组织面向两种不同使命时，呈现出的不同层次结构进行了挖掘和对比，但其本质思想仍是静态分析，在未来的工作中，我们应该更多考虑对结构的动态演化特征进行挖掘和学习，能够进一步对结构未来的变化进行准确预测。

［1］ Wasserman S，Faust K.Social Network Analysis［M］.Cambridge：Cambridge University Press，1994.

［2］Scot J.Social Network Analysis：A Handbook［M］.2nd.London：Sage Publications Ltd，2000.

［3］ Faloutsos M，Faloutsos P，Faloutsos C.On power－law relationships of the internet topology［J］.Computer Communication Review，1999，29：251－262.

［4］Pastor－Satorras R，Vespignani A.Evolution and Structure of the Internet［M］.Cambridge：Cambridge University Press，2004.

［5］ Barabasi A－L，Oltvai Z N.Network biology：understanding the cell′s functional organization［J］.Nature Reviews Genetics，2004，5（2）：101－113.

［6］ Barabasi A－L，Gulbahce N，Loscalzo J.Network medicine：a network based approach to human disease［J］.Nature Reviews Genetics，2011，12（1）：56－68.

［7］ Lane D.Hierarchy，Complexity，Society［M］.Dodrecht，the Netherlands：Springer，2006：81－120.

［8］ Memon N，Larsen H L，Hicks D L，et al.Detecting hidden hierarchy in terrorist networks：Some case studies［C］／／Proceedings of the IEEE ISI 2008PAISI，PACCF，and SOCO international workshops on Intelligence and Security Informatics.Berlin，Heidelberg：Springer－Verlag，2008：477－489.

［9］Seidman S.Network structure and minimum degree［J］.Social Networks，1983，5：269－287.

［10］Daniel W M.The hierarchical structure of organisms：a scale and documentation of a trend in the maximum ［J］.Paleobiology，2001，27（2）：405－423.

［11］Wimberley E T.Nested ecology.The Place of Humans in the ecological Hierarchy［M］.Baltimore，MD：John Hopkins University Press，2009.

［12］Newman M E J.Detecting community structure in networks［J］.European Physical Journal B，2004，38（2）：321.

［13］Fortunato S.Community detection in graphs［J］.Physics Reports，2010，486：75－174.

［14］Newman M E J.Communities，modules and large－scale structure in networks［J］.Nature Physics，2012，8：25－31.

［15］Arun S M，Tanya Y B.Inferring the maximum likelihood hierarchy in social networks［C］／／Proceedings of the 2009International Conference on Computational Science and Engineering.Washington DC：IEEE Computer Society，2009：273－283.

［16］Mones E，Vicsek L，Vicek T.Hierarchy measure for complex networks［J］.PLoS ONE，2012，7（3）：e33799.

［17］成清.社会网络的节点重要度和重叠社区发现研究［D］.长沙：国防科技大学.2012.Cheng Qing.Research on node importance evaluation and community discovery in social networks［D］.Changsha：National University of Defense Technology，2012.

［18］付强，赵小勇.投影寻踪模型原理及其应用［M］.北京：科学出版社.2006：47－50.

［19］Premchand S N，Suseela T S.Data mining through fuzzy social network analysis［C］／／Proceedings of the 26th Annual Meeting of the North A－merican Fuzzy Information Processing Society.San Diego：Institute of Electrical and Electronics Engineers Inc，2007：251－255.

［20］刘振亚.面向C2组织效能测度的探索性分析方法研究［D］.长沙：国防科技大学.2009.Liu Zhenya.A research of exploratory analysis for measure of C2organizational effectiveness［D］.Changsha：National University of Defense Technology，2009.

［21］李德毅，杜鹢.不确定性人工智能［M］.北京：国防工业出版社.2005：197－212.

［22］Faloutsos C，McCurley K S，Tomkins A.Fast discovery of connection subgraphs［C］.／／Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining.New York：Association for Computing Machinery，2004：119－127.

［23］Shetty J，Adibi J.The enron email dataset：database schema and brief statistical report［DB／OL］.［2013－07－20］.http：／／www.isi.edu／？adibi／Enron／Enron Dataset Report.pdf

［24］Gilbert E.Phrases that signal workplace hierarchy［C］／／Proceedings of the ACM 2012Conference on Computer Supported Cooperative Work.New York：Association for Computing Machinery，2012：1037－1046.