基于MLP方法的船舶大幅横摇近似解析解*

刘亚冲 胡安康，2 韩凤磊 汪春辉

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨150001;2.中集船舶海洋工程设计研究院，上海201206)

在长期的研究过程中研究者发现利用线性模型来描述船舶的横摇运动与实际情况相差甚远，且线性模型无法得到非线性所具有的一些诸如跳跃、分岔、混沌等现象［1-4］.由于船体几何外形原因，在船舶发生大角度横倾时船舶横摇的恢复力矩本身即具有非线性，而由于真实流体具有粘性，横摇阻尼也具有非线性特征.因此研究船舶的非线性横摇运动，对非线性横摇运动进行解析求解具有重要的实际意义.

对船舶非线性横摇阻尼的处理，目前有线性项加平方项(LPQD)方式即和线性项加立方项(LPCD)方式即.Bikdash 等［5］对不同的阻尼模式进行了研究分析.从计算分析角度来看，LPCD 模式无疑方便处理，因为该阻尼模式避免了因绝对值的存在给数学分析带来的困难.船舶恢复力矩是横摇角φ 的函数，考虑到船舶关于中线面的对称性，可以用奇数次的高阶多项式函数来拟合，那么非线性恢复力矩可以表示为M(φ)= C1φ + C3φ3+ C5φ5+ …，通常取前两项即可很好地模拟静稳性曲线.

传统的L-P 方法对于弱非线性系统的求解是可行的，若将其应用于强非线性系统则会带来较大误差.文中采用改进的L-P 法(即MLP 方法)对船舶的非线性横摇问题进行求解，分别得到静水中和规则波中的近似解析解，并用数值计算来验证该方法的正确性.

1 船舶非线性横摇运动方程的建立

考虑阻尼力矩和恢复力矩的非线性，船舶的非线性横摇运动方程可以表述为:

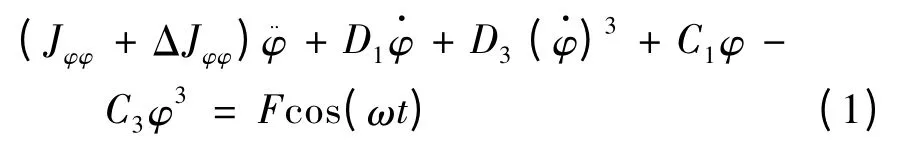
式中:Jφφ、ΔJφφ为转动惯量和附加转动惯量;D1为线性阻尼力矩系数，可以通过势流理论求得;D3为非线性阻尼力矩系数，可以通过横摇衰减试验［6-7］或CFD 仿真［8-9］得到;C1为线性恢复力矩系数，C1=D，D 为船舶排水量，为船舶初稳心高;C3为非线性恢复力矩系数;C1和C3可以由船舶静稳性曲线得到.式(1)右端表示波浪激励项［10］，F = D·GMkξ，k 为波数，ξ 为波高，ω 为波浪圆频率.式(1)两边同除以(Jφφ+ ΔJφφ)后，可将式(1)写为

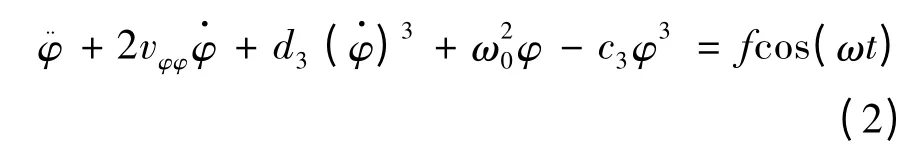
式中:2vφφ为横摇衰减系数，2vφφ= D1/(Jφφ+ ΔJφφ);ω0为船舶横摇近似固有圆频率，ω20= C1/(Jφφ+ΔJφφ);d3= D3/(Jφφ+ΔJφφ);c3= C3/(Jφφ+ΔJφφ);d =D/(Jφφ+ΔJφφ)，引入参数ε，为便于表示，设，将式(2)表达为拟线性系统的形式:

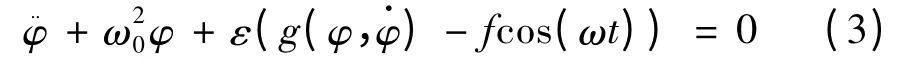
2 改进的L-P(MLP)法

对于非线性动力方程(3)的求解，摄动方法是进行近似解析求解的行之有效的方法.常规的摄动方法如直接摄动法、LP 法、平均法、KBM 法和多尺度法等只能对弱非线性的动力方程进行近似解析［11］.当方程(3)中的参数不能满足ε ≪1 时，针对弱非线性系统的摄动法会带来求解误差，鉴于此，文中采用改进的L-P 方法(Modified L-P 法，简称MLP方法［12］)对式(2)进行求解.

2.1 自由横摇的二阶近似解

首先求解船舶自由横摇的二阶近似解析解，令方程(2)右端激励项为零即可，此时横摇方程为

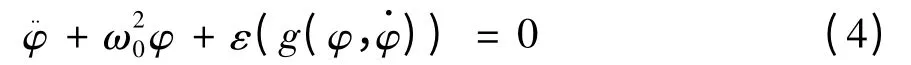
方程(4)中的ε 不再限定为小参数.引入新的自变量 = ωt，ω 代表待求的原系统的非线性频率，于是式(4)变为

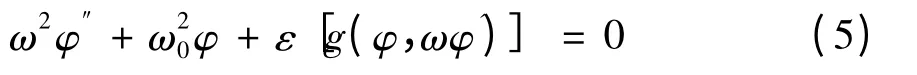
式中，φ'表示φ 对 的一阶微商，φ″表示φ 对 的二阶微商.将ω2在ω0附近展开为ε 的幂级数，即

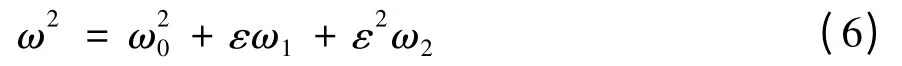
然后，引入一个参数变换

于是总有0 ＜α ＜1 成立，并且

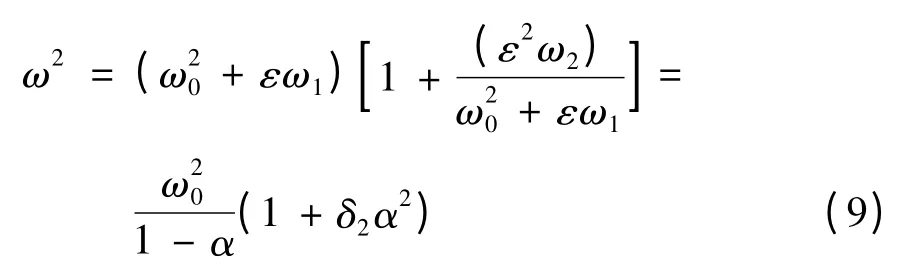
将式(8)和(9)代入方程(5)得

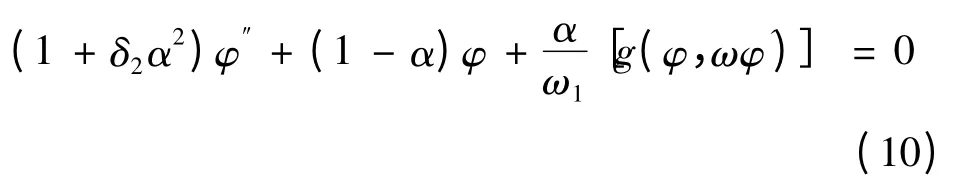
式中，α、δ2为待定的未知常数.将φ 展开成新参数α 的幂级数，对自由横摇取前两阶近似解有

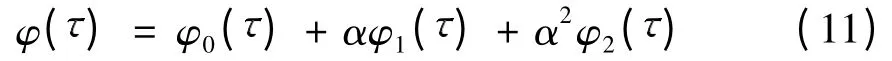
将式(11)代入式(10)，令两端α 的同次幂相等，得:

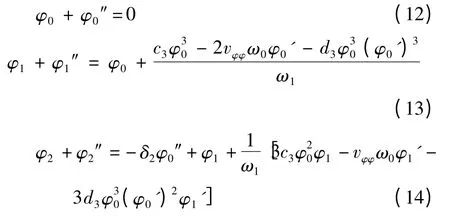
考虑初始化条件φ0(0)= a0，φi(0)= 0 (i =1，2)，φj'(0)= 0 (j = 0，1，2)，式(12)的解为φ0()= a0cos ，将φ0()代入式(13)，消去久期项得

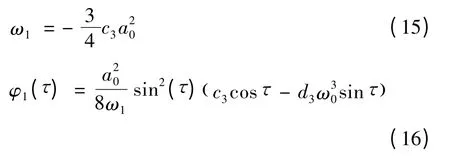
于是，新参数为

将式(15)、(16)代入方程(14)，根据久期项为0 的条件可以求出δ2和φ2().

最终，求得精确至o(α3)的解为

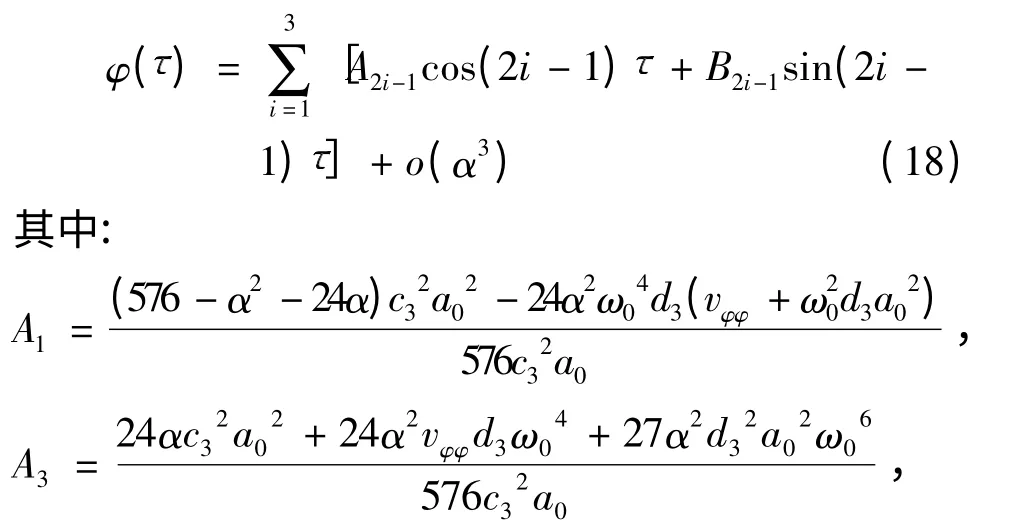
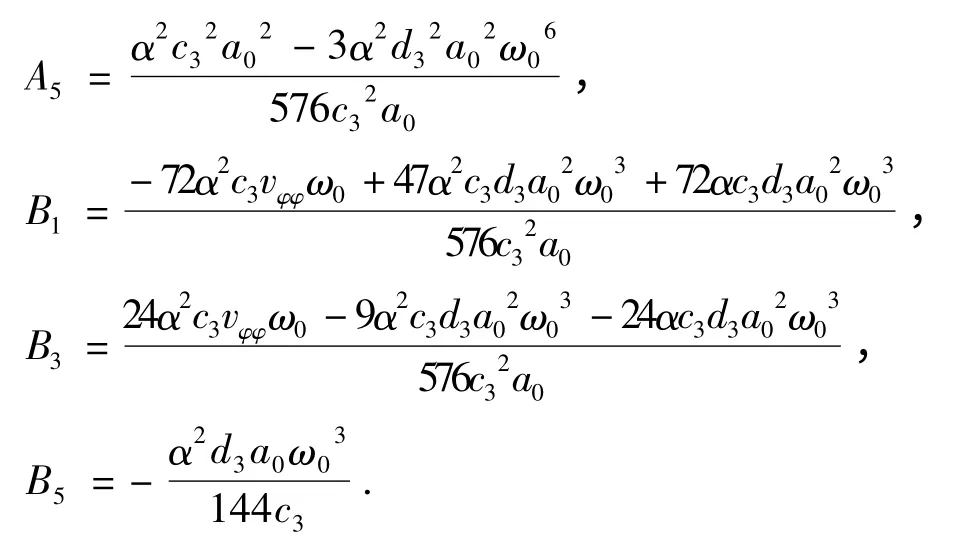
2.2 规则波中的一阶近似解

规则波中船舶非线性横摇方程可写成

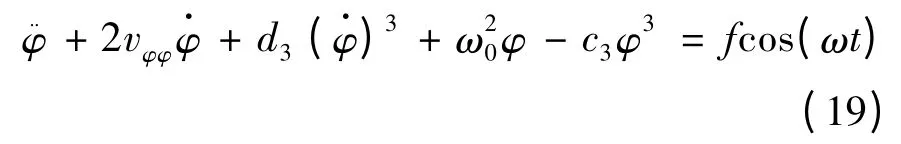
同样，引入新的自变量 = ωt，式(19)成为

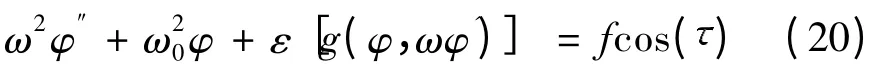
将ω2在ω0附近展开为ε 的幂级数，并将φ 展开成α的幂级数.将ω2和φ 代入式(19)，令两端α 的同次幂相等得:

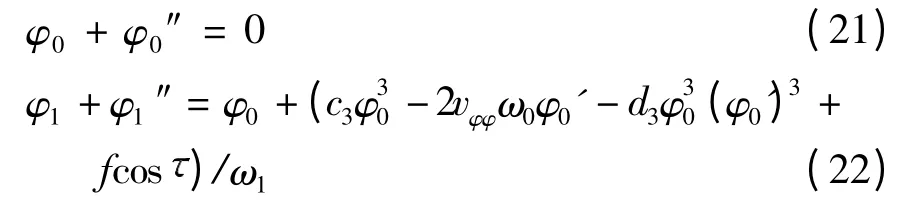
此时，初始化条件为φ0(0)=a0;φ1(0)=φ1'(0)=0，式(21)的解为φ0()= a0cos +Csin ，C 为待定常数，可在下面的式(23)中求出.将φ0()代入式(22)，得到久期项为0 的条件为

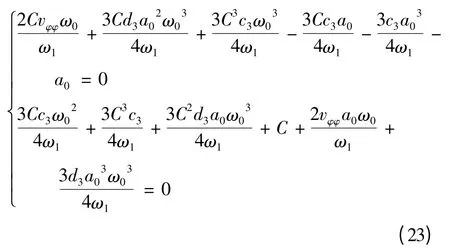
根据式(23)，可求出ω1和C，见式(24)和(25).

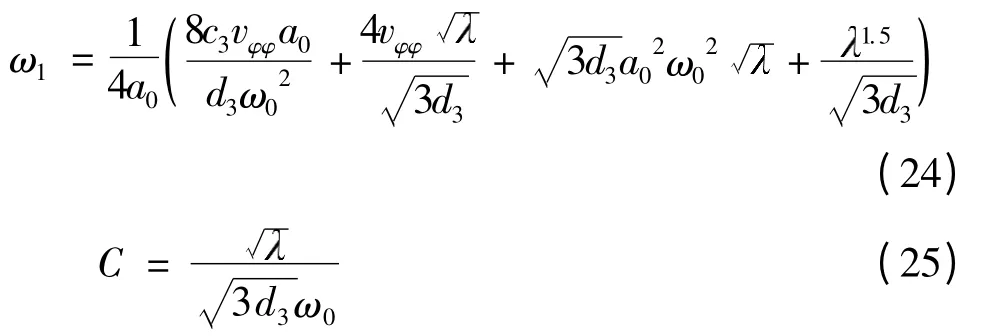
3 数值算法

在文中，数值算法选择高精度单步算法四阶Runge-Kutta 法，对于高阶微分方程式(19)，首先要将其降阶化为一阶微分方程组.不妨选取φ = φ1，，于是有

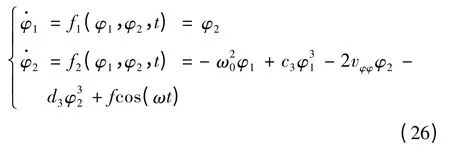
若采用向量的记号，记φ = (φ1，φ2)T，f =(f1，f2)T，并考虑初值条件，则有式(27)成立.

求解这一初值问题的四阶Runge-Kutta 公式为

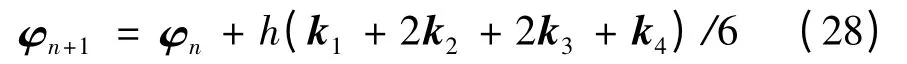
式中，

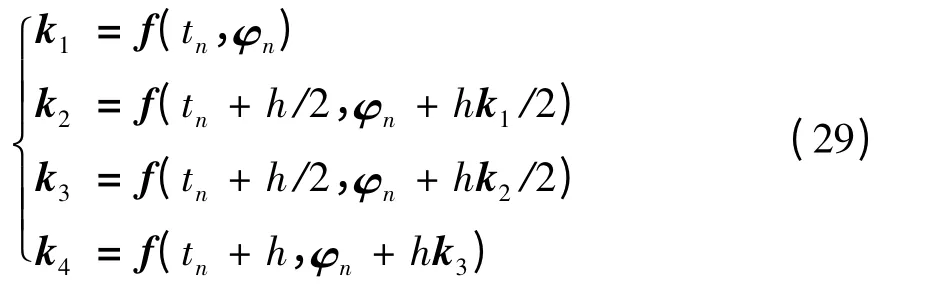
根据式(28)和(29)，考虑到初始条件后就可以编制相应的计算程序进行时间步进求解.

4 算例分析

为了便于分析比较，文中选取Gaul 拖船［13］作为算例.分别采用MLP 法和数值算法对算例进行计算，以验证MLP 法的有效性.该拖船的主要特征参数见表1.

表1 算例参数Table1 Parameters of example

首先选取静水工况，不妨选取10°的初始横倾角，即φ(0)= 0.175 rad，采用数值算法和采用MLP得到的横摇运动的时历图与Poincare 截面见图1.

图1表明采用MLP 法获得的二阶近似解与采用Runge-Kutta 法得到的数值解吻合较好.由于MLP法获得的横摇近似解只精确至二阶，与更高阶有关的横摇频率的信息无法体现，因此近似解析解与数值解之间有一些细微的差别，在时历图中则表现为沿时间轴方向有一些偏移.

对于规则波中情形，为使选取的波浪参数不失一般性，文中在Gaul 船的横摇固有频率附近选择3个不同的波浪激励频率，根据深水色散关系可以求出波浪参数的波长，根据波陡概率密度分布函数［14-15］，可以得到3 个波浪频率对应的波高.由此得到的3 个波浪参数见表2.

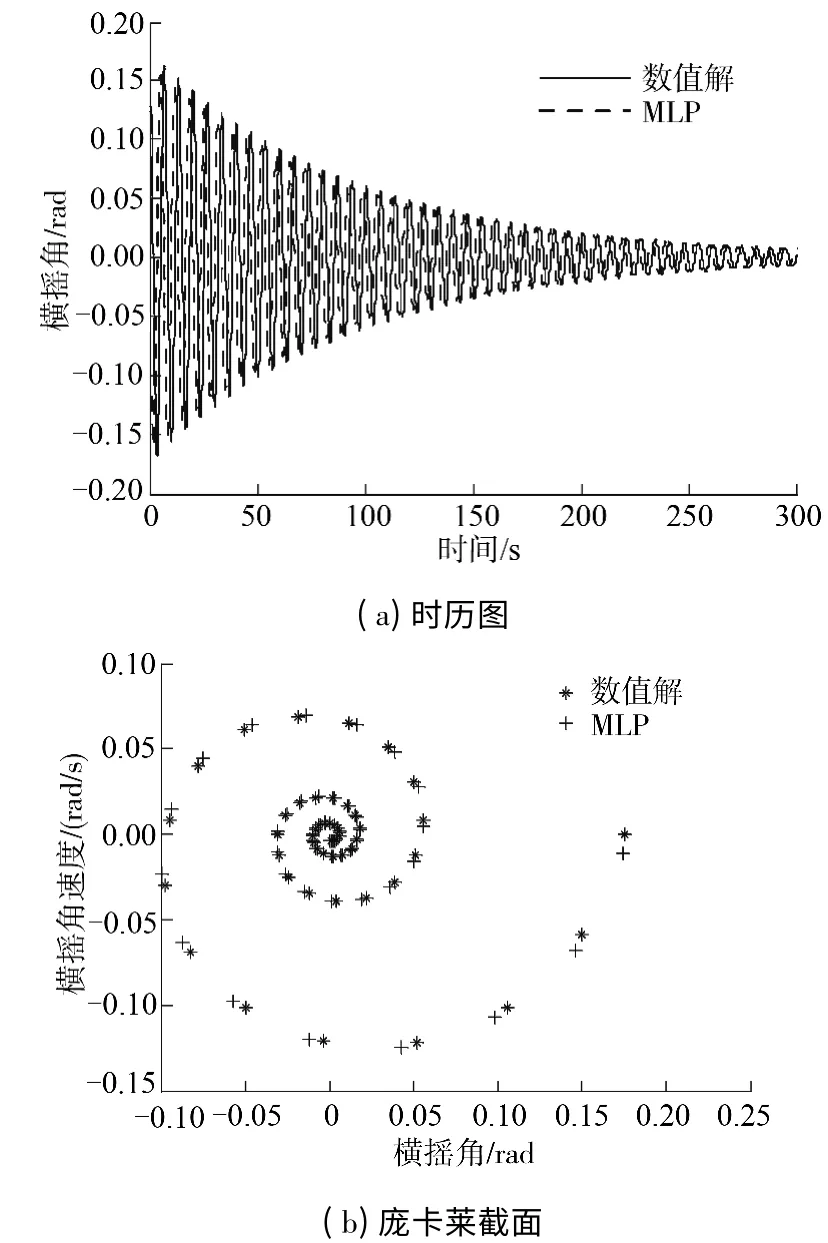
图1 自由横摇的时历图与Poincare 截面Fig.1 Free-roll time-domain diagram and Poincare section

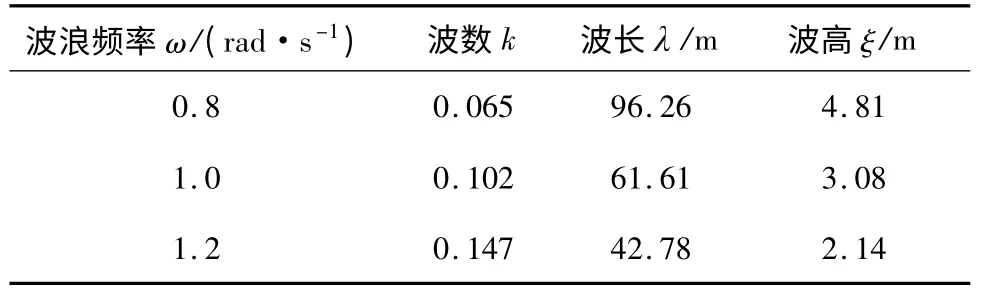
表2 波浪参数Table2 Wave parameters

分别对表2表示的3 种波浪激励进行数值求解，并根据MLP 进行摄动求解，得到的结果见图2.其中图2(a)、2(c)和2(d)为两种方法得到的时历图，图2(b)为相图.

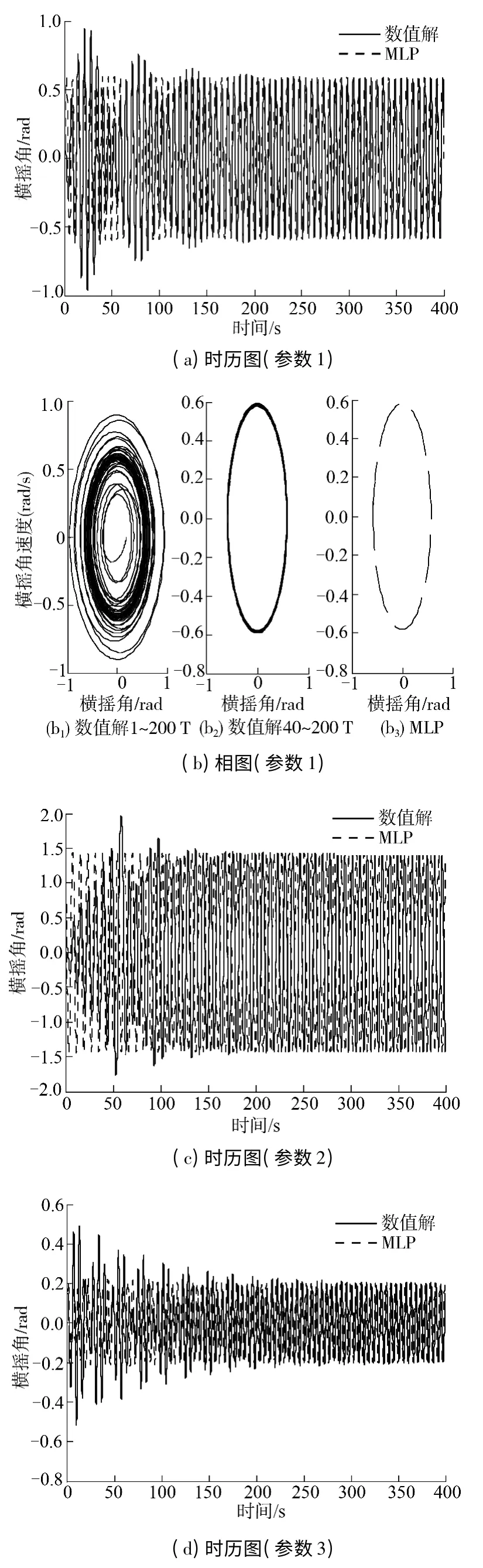
图2 规则波作用下的时历图与相图Fig.2 Time-domain diagram under regular wave

从以上3 个时历图中可以看出数值解在前200 s的时间内有波动现象，然后逐步稳定到稳态的周期运动;从图2(b)相图也可以看出，对于第1 组波浪参数，从第40 个周期开始横摇就已经是稳定的周期运动，而MLP 求得的是系统稳定横摇阶段的解.从波浪的激励频率角度来看，当激励频率与横摇派生系统的固有频率接近时，横摇的运动幅度达到最大，此时对应系统的主共振情形.

5 结论

文中采用MLP 法对船舶非线性横摇运动进行近似解析求解，分别得到了静水中自由衰减运动的二阶近似解析解和在不同波浪参数规则波作用下的一阶近似解析解.通过将解析解与Runge-Kutta 法得到的数值解进行对比分析，验证了MLP 法求得的近似解的正确性.由于近似解析解略掉了与高阶项有关的固有频率，因而与数值解有细微的差别.

在MLP 方法中，通过引入参数变换，将ω2在展开可以使得对于任何的εω1，总能使新参数α 满足0 ＜α ＜1，这样就可以将原来相对于ε是强非线性的系统转化为相对α 是弱非线性系统，这对于研究船舶的大幅横摇运动和进行横摇稳性评估具有重要意义.

［1］Nayfeh A H，Sanchez N E.Stability and complicated rolling responses of ship in regular beam seas［J］.International Shipbuilding Progress，1990，37(410):177-198.

［2］Taylan M.Static and dynamic aspects of a capsize phenomenon［J］.Ocean Engineering，2003，30(3):331-350.

［3］Francescutto A.Intact ship stability:the way ahead［J］.Marine Technology，2004，41(1):31-37.

［4］李远林.船舶非线性大幅横摇导致倾覆的研究［J］.华南理工大学学报:自然科学版，2001，29(6):91-96.Li Yuan-lin.Research in nonlinear large-amplitude roll leading to capsize in wind-waves ［J］.Journal of South China University of Technology:Natural Science Edition，2001，29(6):91-96.

［5］Bikdash M，Balachandran B，Nafey A H.Melnikov analysis for a ship with a general roll-damping model［J］.Nonlinear Dynamics，1994，6(1):101-124.

［6］李红霞，唐友刚，胡楠，等.船舶横摇非线性阻尼系数的识别［J］.天津大学学报，2005，38(12)1042-1045.Li Hong-xia，Tang You-gang，Hu Nan，et al.Identification for Nonlinear Ship Roll DampingCoefficients［J］.Journal of Tianjin University，2005，38(12):1042-1045.

［7］李远林，伍晓榕.非线性横摇阻尼的试验确定-数据处理方法［J］.华南理工大学学报:自然科学版，2002，30(2):79-82.Li Yuan-lin，Wu Xiao-rong.Experimental determination of nonlinear roll damping:a technique for data processing［J］.Journal of South China University of Technology:Natural Science Edition，2002，30(2):79-82.

［8］朱仁传，郭海强，缪国平，等.一种基于CFD 理论船舶附加质量与阻尼的计算方法［J］.上海交通大学学报，2009，42(2):198-203.Zhu Ren-chuan，Guo Hai-qiang，Miao Guo-ping，et al.A computational method for evaluation of added mass and damping of ship based on CFD theory ［J］.Journal of Shanghai Jiao Tong University，2009，42(2):198-203.

［9］黄昊，郭海强，朱仁传，等.粘性流中船舶横摇阻尼计算［J］.船舶力学，2008，12(4):568-573.Huang Hao，Guo Hai-qiang，Zhu Ren-chuan，et al.Computations of ship roll damping in viscousflow［J］.Journal of Ship Mechanics，2008，12(4):568-573.

［10］李积德.船舶耐波性［M］.哈尔滨:哈尔滨工程大学出版社，2001.

［11］胡海岩.应用非线性动力学［M］.北京:航空工业出版社，2000.

［12］陈树辉.强非线性振动系统的定量分析方法［M］.北京:科学出版社，2007.

［13］Morrall A.The gaul disaster:a investigation into the loss of a large stern trawler［J］.Naval Architect，1981(5):391-440.

［14］高志一，文凡，李洁.波群内单个波的波陡分布与破碎波［J］.海洋科学，2011，35(9):96-106.Gao Zhi-yi，Wen Fan，Li Jie.The steepness distributions and break of individual waves in wavegroups［J］.Marine Science，2011，35(9):96-106.

［15］裴玉华，郑桂珍，丛培秀.海浪的波陡分布［J］.中国海洋大学学报，2007，37(7):73-77.Pei Yu-hua，Zheng Gui-zhen，Cong Pei-xiu.The probability distribution function of wave steepness ［J］.Periodical of Ocean University of China，2007，37(7):73-77.