粘土超声波速度变化因素研究

2015-12-19王飞声

西部探矿工程 2015年11期

关键词：原状波速土样

王飞声

(昆山华一岩土勘察工程有限公司，江苏苏州215300)

·岩土工程·

粘土超声波速度变化因素研究

王飞声*

(昆山华一岩土勘察工程有限公司，江苏苏州215300)

波速测试作为一种测试手段，已经在诸多领域取得了成功。这里将波速测试运用于南京地区常见的粉质粘土中，研究了在不同环境、不同压力作用之下，土样的含水率、孔隙比和纵波波速的变化。结合压缩条件下土体微结构变化和平均波速公式，尝试解释原状土样和扰动土样，二者在分级侧限压缩试验之下，所对应的波速变化。研究结果表明，含水量的变化跟波速的增大呈现正相关的趋势；而同时，孔隙比的变化跟波速则体现出了负相关的关系。为了能够进一步地阐述这一变化机制，这里引入了孔隙水压力和有效应力的概念，以二者的相对变化趋势来研究在描述固液气三相的体积变化，从而为解释2种不同状态的粉质粘土中波速的异常行为提供了理论基础和实例参考。

粉质粘土；超声波检测；波速异常；压力

1 概述

超声波检测作为一种无损、快速、简便的检测方法在岩土工程探测已被广泛应用，并趋于成熟，被越来越多的用于试验研究当中。国内在岩土体完整性检测与评价及强度预测、混凝土强度检测方法、波速与埋深的关系等固体超声测定方面的技术已相当成熟：如陈烨[1]从波速、波形和频谱特性的角度来综合研究水泥土的质量和强度，陶莅宁等[2]则是根据地表脉冲在地层分界处传播的差异，介绍了波速测试的原理；陈昌军[3]则是从剪切波波速测试的角度，对影响波速测试的因素做了相关的探讨。然而对于工程应用中比较常见的粘土[4]，超声波对应的研究却偏少，拾峰[7]、王峥辉[5]等虽然探讨了粘土含水量和压缩系数随波速的变化情况，并给出了关于波速拟合曲线的解析式，但是并没有清晰的关于波速跟孔隙水压力、有效应力二者之间的表述。

本文从相关土样中选出2大组不同状态的粉质粘土为试样，进行侧限压缩研究。同时借鉴地球物理中岩石速度时间平均公式，尝试从侧限压力、含水率、孔隙比3个角度，解释粉质粘土中引起波速变化的原因。

2 试验装置、方法和试样的制作

2.1 试验装置

本次试验采用的是武汉沿海公司生产的RSST01C非金属声波检测仪，RS-ST01C集电子技术、计算机技术、声发射技术于一体，是低耗、高效、稳定、便携的新一代智能化测试技术。

2.2 试验方法

对采集的土样按照0kPa、50kPa、100kPa、200kPa和400kPa压力下，分5个阶段分别进行侧限固结压缩试验。每个阶段开始之前都需要先进行土工试验，然后采用超声波脉冲透射法，以凡士林作为耦合剂，在试样的一端用发射器发射超声脉冲波，同时试样的另一端接收换能器接收。当超声波在试样中传播后，另一端所接收到的超声波信号则转化为相应的电信号，通过超声波放大器放大，就可以得到转换后的数字信息。

2.3 试样制作

选取南京某段工程中的粉质粘土作为试验试样，用薄壁取土器取粉质粘土原状土，取24个样，取样方法和试样尺寸严格按照《原状土取样技术标准》（JGJ89-92）进行：取得试样之后，采用环刀法，制作了如图1、图2所示的2组试样：原状土样（Y）(图1)、扰动土样（R）(图2)。

所谓原状土样，即通过环刀法采集原状土样，并将试样放入固结仪内，上下放透水石，透水石贴近试样的面要加滤纸，以便排水；扰动土样，即不同之处是将获得的原状土倒入击实筒内，按照《土工试验方法标准》(GB/T50123-1999)中击实试验的轻型击实试验方法进行击实，取出击实样用环刀进行切取，得到击实扰动土样[7]。

图1 原状试样

图2 扰动试样

3 速度平均方程的选用

自然界中的土是由固相(固体颗粒)、液相(土中水)和气相(土中气体)组成的，是三相分散体系[8]。这里可以借鉴伍德提出的，时间—平均方程[10]：

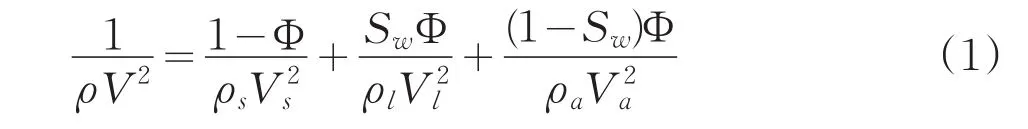
式中：V——岩石介质中超声波的速度；

Vs——固体骨架中的超声波速度；

Vl——充填物的波速，可近似等于即超声波在水中的速度；

Φ——孔隙比；

Va——空气中的波速；

Sw——含水饱和度，水所占的孔隙的体积与岩石孔隙体积之比；

ρa、ρl、ρs——空气、流体和固体骨架中超声波的速度。

综上所述，波速的大小跟三相所占的体积比例有着直接的关系。

4 实验结果分析及讨论

试验测定了5种侧限压力之下2种不同土样所对应的波速、含水量和孔隙比。对2种不同状态的土样在不同侧限压力环境中分别进行了压缩试验，将测量的相关试验数据进行换算处理后得到各物理性质指标，而波速则可以通过声波仪直接读出。

4.1 波速随着压力的变化异常情况

按照2.2节所述试验方法，对粉质粘土原状土样和粉质粘土扰动土样在各个压力之下的试验数据进行分析，将物理性质指标和纵波波速数据总结之后，绘制成图，通过图像的直观表达，显现出波速随物理性质变化的趋势，进而分析研究得出相关结论。

如图3所示，随着压力的增大，原状土样中压力呈现出先减小，再增大，最后再减小的趋势，总体上，波速跟压力两者总体呈现反比的特性；而与原状土不同的是，随着压力的增大，扰动土样中（图4），虽然在100～200kPa区间体现一定的波动，但总体上，随着压力的增加，波速呈现出上升的趋势。

这样2种不同状态之下的粉质粘土中，波速跟压力呈现出迥然相反的趋势。原状土样，波速跟压力呈现反比趋势，而扰动土样中，则是呈现出正比的趋势。

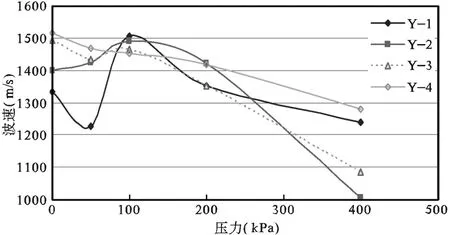
图3 原状土样中速度—压力变化曲线图

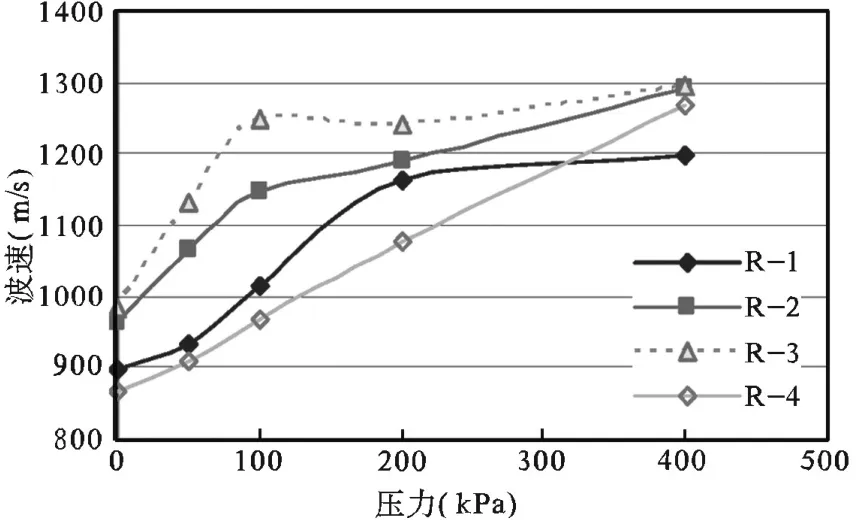
图4 扰动土样中速度—压力变化曲线图

4.2 含水率在静压试验中的变化

根据上一节中制备的试样进行试验，可以得到相应压力级别之下含水率的指标，试验结果如下所示：

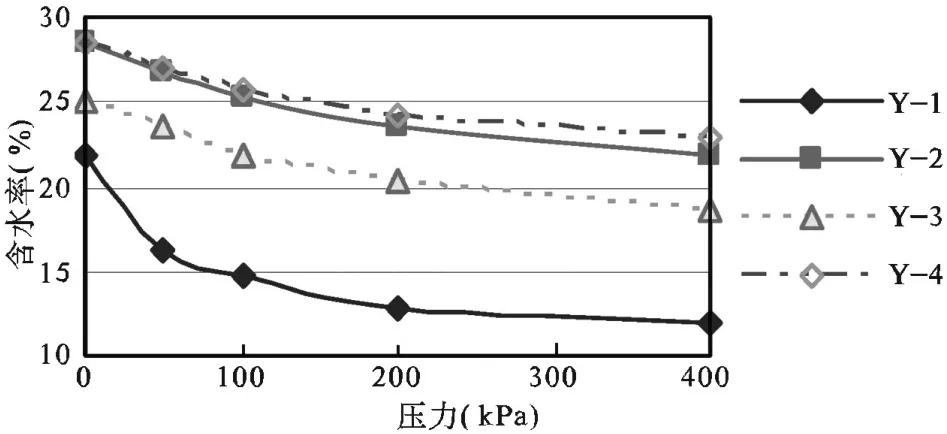
图5 原状土样中含水率的变化

由图5原状土含水率的变化可知，在这一过程中，某一压力区间之内（即0～100kPa压力之间处），含水率的下降速度偏大，而之后的应力范围内（即100～400kPa压力之间处），变化则趋缓；对应上图3可知，在这一区间，波速也出现了扰动，这说明在这一压力区间，含水量的损失，跟波速的扰动二者之间存在一定的关系。

同样，扰动土样中（图6），水量的流失也存在类似的变化趋势，只是其幅度远远小于原状土样中水分的流失。

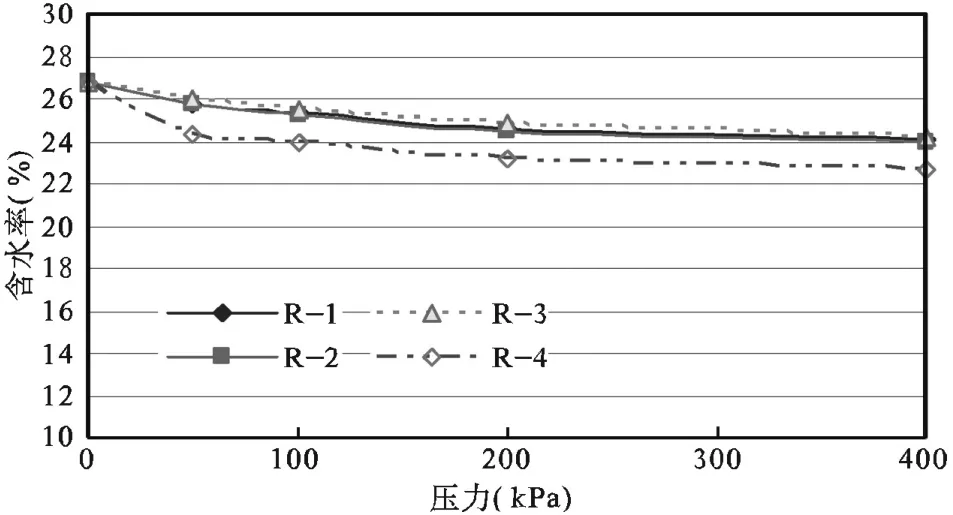
图6 扰动土样中含水率的变化

4.3 孔隙比在静压试验中的变化

同样，根据上一节中的试样进行试验，可以得到相应压力级别之下孔隙比的变化趋势，试验结果如下所示：

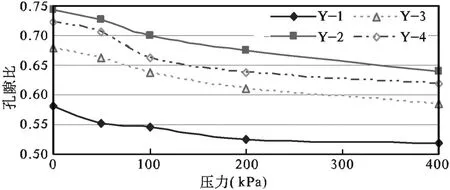
图7 原状土样中孔隙比的变化

孔隙比方面，孔隙比表示的是土中孔隙体积与颗粒体积的比值。在压缩固结过程中，假设颗粒不被压缩，也就是固体颗粒总体积不变，所以孔隙比的减小直接代表的就是孔隙总体积的减小。而孔隙体积的变化则是体现在有水孔隙和无水孔隙二者的体积变化，而水的体积无法压缩，所以体积的变化主要体现在无水孔隙的变化中。

结合图7可知，其在波速界限含水率后(1～2级压力之间)，孔隙比下降的幅度保持了一个相对稳定值。但是在1～2级压力之间，平均孔隙比变化相对比较大。这主要是由于在这段区间内，压力主要由孔隙水压力承压，导致水的流失加剧，而同时，在100kPa之后，土体结构逐渐完成了重新固结，有效应力变大，而此时孔隙水压力也相应的减小，同时残余孔隙水逐渐被封存进孔隙，不容易被排出，进而导致孔隙水含量减小幅度变弱，这在图3中也有所体现。

在扰动土样中（图8），也有着类似的规律，但是扰动土样中孔隙比的变化幅度明显偏小，这应该是因为，扰动土样的制备过程中，土样击实，土颗粒经过重新排布，此时，压力主要由固体骨架承担，而孔隙水压力分担压力的作用，此时并没有得到充分发挥。

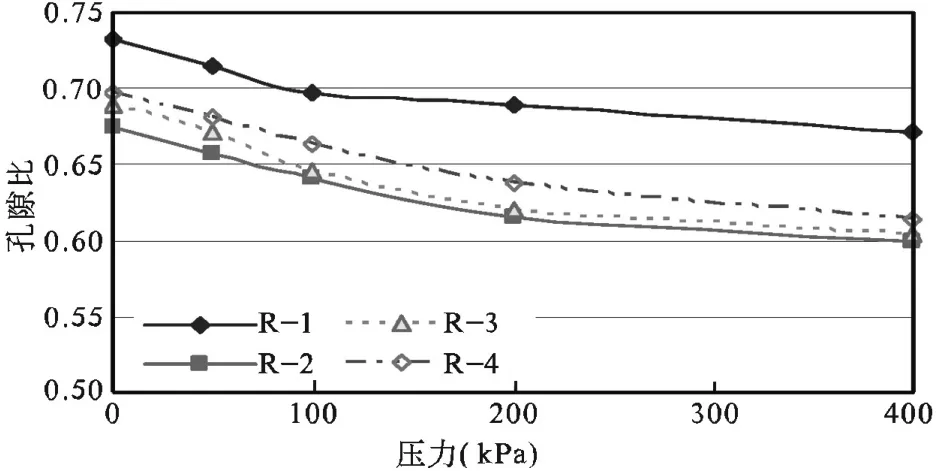
图8 扰动土样中孔隙比的变化

因此综合以上的观点，可以近似得出在原状土样中，含水率的变化对波速影响占主要因素，而在扰动土样中，孔隙比的变化则是主要影响因素。

5 原因解析

这里主要根据式1中，固液气三相体积的变化来解析波速的变化。粘土的变形通常以K.Terzaghi的固结理论为依据，可以大致分为两部分：由孔隙水压力所引起的孔隙压缩和骨架有效应力所发生的骨架变形[9，11]。

第一阶段（0～100kPa），属于结构恢复期，由于土样暴露在空气中，导致土样中的自由水开始挥发，同时在荷载的作用下，孔隙水压力和骨架有效应力开始发挥作用，但是此时，土样处于结构恢复阶段，所以土质松散，因此这一过程中一部分荷载将由孔隙水压力承担，从而加快了孔隙水的流失，并在土样中留下了大量的无水孔隙。然而，这一过程中，粒间连结没有发生大的变化，而流体所占体积减小，同时，气体的体积所占比例则在相应的增大。结合式（1）可知，这一过程中，土中的含水量成为了控制纵波波速的主要因素，即含水率越大纵波波速越大，而含水率越小减少则波速降低，而在此之后，随着压力的继续增大，孔隙水压力逐渐减小，而有效应力增大，此时，水的流失速度减小，所以，对于大部分土样，这段时期之内，波速则是开始上升，这在图3和图4的体现就是，波速随着压力的增长先减小，后增大。

而在扰动土样中，由于击实作用，使得式样中的土颗粒已经完成了结构重组，液体的流失在这一过程中，表现得并不如原状土样那么明显。这在图5、图6中有所反映。而同时，由于土体的击实重构，使得在这一过程中，土体变形减小，即孔隙比变化幅度变小，这在图7、图8中有所体现。经过这两方面的对比，可以发现对于扰动土样，荷载主要是由固体骨架承担荷载，所以直接导致骨架的体积缩小，对应着气体体积的减小，所以可以推断，这一阶段中，扰动土中的含水率对波速的影响有限，而同时孔隙比对波速的影响加大。

第二阶段（100～400kPa），原状土样中，荷载开始从孔隙水压力向固体骨架转移，在这一过程中，土的密实度增大，孔隙连通率减小，孔隙中自由水的含量减少，不过其减小幅度在变小。而压力的增大，使得原有的孔隙骨架间的有效应力己经不能适应增大后的压力，发生了颗粒的崩解向细粒转化，此时，部分结合水变成了自由水，弥补了部分流失的自由水。同时细化后额颗粒填补了孔隙，使得孔隙减小。对比图5～图8可知，这一过程中，原状土样和扰动土样的孔隙率变化幅度类似，而同时，原状土样含水量的变化是扰动土样的3-4倍，这表明在这一过程中，原状土样中的水的流失的速度仍然大于固体骨架固结的速度，即在这一过程中，流体所占体积比例进一步减小，而同时，气体所占相对体积比例增加。结合式1可知，此时波速仍然在变小，只是变小的幅度变小，这在图3中有所体现。

而扰动土样在这一阶段中，则是土体的骨架在应力的作用之下则是进一步加强，而同时，由于孔隙比的减小，颗粒间的通道被截断，导致更多的自由水被禁锢在孔隙中，水的散失量在减小，但总体上，荷载是由固体骨架承担，所以这段时期内，孔隙比的变化对波速产生的影响还是大于含水量对波速产生的影响。

6 结论与展望

本文针对原状和扰动2种不同的粉质粘土式样在侧限压缩下，超声波波速的变化情况，结合岩石中超声波时间平均波速方程，从孔隙比、含水率这2个角度阐述了波速变化的原因，试验结果表明：

在表观因素中，纵波波速与土的含水率、孔隙比、外力条件等物理力学性质指标之间有着很好的相关性，含水率与纵波波速是正相关的，孔隙比与纵波波速是负相关的。但是它们的变化在土中不是单纯变化，而是同时作用的相互联系着变化，而它们各自对波速也有着自己的对应影响规律，所以它们对纵波波速的影响因素既有规律性也存在不确定性。

在试验研究的过程中，除了以上的结论外，仍然存在着有待解决的问题：

在研究试验数据中，能发现，原状土样在某一应力区间内（50～100kPa），试样中的孔隙水压力和有效应力二者之间发生了类似于“接力棒”的角色转换，但是这一个点具体在什么地方发生，在其他土式样中，是否也有着类似的过程，这个有待进一步查明。如果能够直接测量孔隙水压力和有效应力两者的变化情况，则能够客观地观测到二者变化的情况。

[1]陈烨,简文彬,林生凉,等.水泥土的超声波特性研究[J].福州大学学报：自然科学版，2006(1)：130-133.

[2]陶莅宁，侯广春.波速测试技术在工程地质勘察中的应用[J].山东煤矿科技.

[3]陈昌军.场地剪切波波速测试及其应用[J].华南地震，2003，23(4)：81-86.

[4]黄文熙.土的工程性质[M].北京：水利电力出版社，1983.

[5]王峥辉,杨凤根,徐建龙.粘性土物理力学性质与超声波波速关系的试验研究[J].江苏地质，2007(3)：99-102.

[6]周绪文.反射波地震勘探方法[M].北京：石油工业出版社，1989.

[7]拾峰.超声波法反演粉质粘土物理力学性质试验研究[D].河海大学，2010.

[8]王盛源.饱和粘性土主固结与次固结变形分析[J].岩土工程学报，1992(5)：72-77.

[9]王峥辉.下蜀黄土超声波波速与物理力学性质试验研究[D].河海大学，2007.

[10]郑志华,张志毅,王德润.超声波法测试干砂试样剪切模量的试验研究[J].世界地震工程，2002(4)：64-67.

[11]胡瑞林，李向全.粘性土微结构定量模型及其工程地质特征研究[M].北京：地质出版社，1994.

P631.5