基于亥姆霍兹线圈的大尺寸均匀电磁场模拟

黄松涛，张伟，张鹏飞，祁泽武

(1.北京石油化工学院 机械工程学院，北京102617;2.北京航空航天大学 机械工程及自动化学院，北京100191)

外层空间指的是地球大气层及其他天体之外的虚空区域.外层空间含有密度很低的物质，以等离子态的氢为主，温度变化剧烈，还有空间辐照、电磁场等.其中，空间电磁场环境效应对航天器的负面影响是长期的、潜在的，尤其对航天器姿态控制系统(比如光纤陀螺等)的影响是一个长期的累积过程.随着航天器长寿命、高可靠性要求的提高，空间电磁场环境效应研究的重要性日显突出，模拟空间电磁环境对航天关键设备进行性能测试和可靠性试验具有十分重要的意义［1］.

自从美国1958年“先锋一号”电磁效应影响飞行任务的事故开始，国内外就开始了航天器磁场环境工程研究.我国先后研制了用于航天器部件磁场环境试验的CM1和CM2超大型弱磁场环境模拟设备，其中CM1的最大线圈边长为4 m，CM2的最大线圈边长为16 m，最大磁感应强度为0.06 mT，目前世界上只有美国、日本和德国有同类设备［1］.而在小尺寸电磁场环境模拟方面，Alamgir和Wang等采用亥姆霍兹(Helmholtz)线圈模拟磁场环境，并对磁场的分布、均匀性进行了深入的研究，其线圈边长一般为100 mm左右，磁感应强度大都低于 0.5 mT［1-3］.

本文针对某型号光纤陀螺性能测试的要求，基于Helmholtz线圈的工作原理，采用一对匝数、边长、高度和厚度相同的共轴平行放置的矩形线圈构成了正方形 Helmholtz线圈(线圈边长为384 mm，线圈中心磁感应强度不低于2 mT)，实现了大尺寸较强磁场环境的模拟［2-7］.采用有限元分析方法，借助ANSYS Workbench分析软件对上述正方形Helmholtz线圈的电磁场进行了分析，在此基础上设计了线圈的结构、匝数、电流等关键参数，并对研制成功的正方形Helmholtz线圈的电磁场分布进行了测量，电磁场的磁感应强度和磁场分布的均匀性均能满足技术要求.

1 电磁场技术指标及构成

根据外层空间物理环境模拟系统的要求，所设计的电磁场主要技术指标如下:

1)磁场强度:±2 mT;

2)磁场的外形尺寸要求:长度≤390 mm，宽度≤390 mm，高度≤350 mm;

3)线圈内部中心200 mm×200 mm×220 mm的区域电磁场差值小于0.2 mT.

根据上述技术要求，基于Helmholtz线圈的工作原理，采用一对匝数、边长、高度和厚度相同的共轴平行放置的正方形线圈来产生所需要的电磁磁场.所设计的电磁场模拟系统主要由正方形Helmholtz线圈、恒流源、单片机控制电路和工控机等组成，如图1所示.

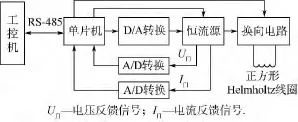
图1 电磁场模拟系统的组成Fig.1 Composition of the electromagnetic field simulation system

在图1中，通过人机交互界面可以设置电磁场的强度，设置好的电磁场工作参数通过RS-485总线传输至电磁场的单片机控制电路，然后再通过D/A转换电路变换成模拟量控制恒流源输出电流的大小.因此，调节恒流源输出电流的大小就可以改变流过正方形Helmholtz线圈电流的大小，从而改变线圈内部电磁场的大小.

恒流源的工作参数:输出空载电压为50V，输出电流0～20 A连续可调.

为了方便监测恒流源的工作状态，单片机控制电路还通过A/D转换电路采集恒流源的输出电压和电流，并通过RS-485总线反馈至工控机进行显示.

通过单片机控制电路还可以切换换向电路，改变流过正方形Helmholtz线圈电流的方向，从而改变电磁场的方向.

2 正方形Helmholtz线圈电磁场模拟

为了精确设计正方形Helmholtz线圈的结构、匝数和励磁电流等关键参数，采用ANSYS Workbench有限元分析软件对该线圈的电磁场分布进行了数值模拟［6-12］.

2.1 正方形Helmholtz线圈轴线上的磁场

正方形Helmholtz线圈指的是一对相同的、共轴的、彼此平行且绕有N匝线圈的正方形载流线圈.如图2所示，正方形Helmholtz线圈的边长为2l，线圈的距离为2a，电流为I，Z轴方向与电流方向形成右手螺旋关系.

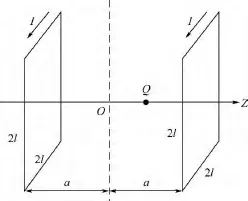
图2 正方形Helmholtz线圈示意图Fig.2 Schematic diagram of square Helmholtz coil

中心轴线上Q处产生的磁感应强度大小为

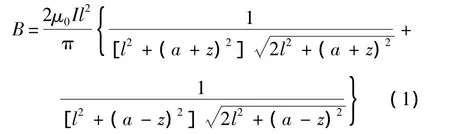
磁感应强度的方向为Z轴方向.

2.2 几何模型

受电磁场模拟系统形状和尺寸的限制，采用一对匝数、边长、高度和厚度相同的共轴平行放置的正方形线圈构成正方形Helmholtz线圈，线圈尺寸如下:

1)线圈外形长宽均为384 mm;

2)线圈的厚度为4 mm;

3)单个线圈的高度为150 mm;

4)两个线圈的中心距离为196 mm.

所设计的正方形Helmholtz线圈的几何模型如图3所示.

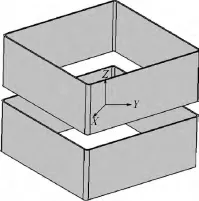
图3 正方形Helmholtz线圈的几何模型Fig.3 Geometrical model of square Helmholtz coil

为了减小电磁场在方框转角处的畸变，提高网格划分质量，转角处进行倒角圆滑过渡.

2.3 材料模型

正方形Helmholtz线圈的材料为紫铜，其磁导率 μ=μ0=4π ×10－7H/m.

2.4 有限元模型

由于正方形Helmholtz线圈模型较为简单，选用自动网格划分法，网格参数物理环境(physics preferance)设定为电磁场(electromagnetics)，网格尺寸的平滑度(smoothing)设定为精细(fine).划分网格后的有限元分析模型如图4所示.

图4 正方形Helmholtz线圈有限元分析模型Fig.4 Finite element analysis model of square Helmholtz coil

2.5 载荷加载

由图1中的电磁场模拟系统构成可知，正方形Helmholtz线圈为恒流源供电，因此在线圈中加载均匀的电流密度Js.

3 计算结果及分析

当在线圈中加载的电流密度 Js=1.25 A/mm2时，采用ANSYS Workbench有限元分析软件进行正方形Helmholtz线圈的电磁场分析，可得到不同位置的电磁场分布.

正方形Helmholtz线圈Z轴的电磁场分布如图5所示.其中，Z轴上的电磁场分布云图如图5(a)所示.为了进一步考察线圈垂直中心线上的电磁场分布，制定路径T1(由1点和2点连线而成，如图5(a)所示)，则T1上各点的磁感应强度分布曲线如图5(b)所示.

从图5可以看出，正方形Helmholtz线圈内部Z轴方向的电磁分布比较均匀，尤其是在Z轴上与1点距离为75mm～275mm区域内电磁场分布更加均匀，磁感应强度差值为0.4 mT以内.

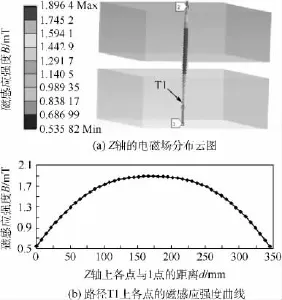
图5 Z轴电磁场分布Fig.5 Distribution of Z axis electromagnetic field

正方形Helmholtz线圈X轴的电磁场分布如图6所示.其中，X轴上的电磁场分布云图如图6(a)所示.为了进一步考察线圈X轴线上的电磁场分布，制定路径T2，由3点和4点连线而成，如图6(a)所示，则T2上各点的磁感应强度分布曲线如图6(b)所示.

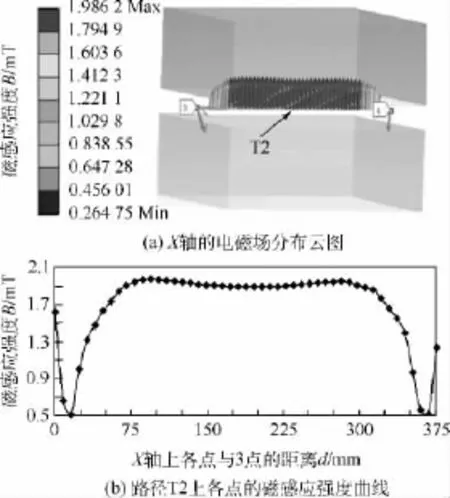
图6 X轴电磁场分布Fig.6 Distribution of X axis electromagnetic field

从图6可以看出，正方形Helmholtz线圈内部X轴线的电磁分布比Z轴更加均匀，尤其是在X轴上与3点距离为75mm～275mm区域内电磁场分布，磁感应强度差值不到0.1 mT.

在距离线圈表面88 mm(比如在 x=0，y=88 mm处)制定平行于Z轴的路径T3(由5点和6点连线而成)，则T3上电磁场分布如图7所示.其中，路径T3的电磁场分布云图如图7(a)所示.路径T3上各点的磁感应强度分布曲线如图7(b)所示.

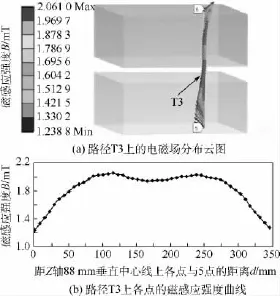
图7 路径T3的电磁场分布Fig.7 Distribution of T3 electromagnetic field

由图7可以看出，与Z轴相比，靠近线圈表面，磁感应强度增大，并且两端的电磁场增加幅度较大，路径T3上的电磁场强度呈驼峰分布，在Z轴方向上电磁场分布更均匀.

由图5、图6和图7的计算结果可以看出，除去线圈内部边缘附近的区域，电磁场的磁感应强度能够达到2 mT，电磁场分布也比较均匀，可以满足测试指标的要求.

4 线圈设计及测试

根据上述计算结果，并结合外层空间物理环境模拟系统实际的结构尺寸要求，所设计的正方形Helmholtz线圈的结构参数如下［13］:

1)正方形Helmholtz线圈由一对匝数、边长、高度和厚度相同的共轴平行放置的矩形线圈构成;

2)单个线圈的外形长宽均为384 mm，高度为150 mm;

3)线圈选择φ1mm的绝缘漆包线，单层绕制150匝，共绕4层，则线圈高度为150 mm，厚度约为4 mm;

4)2个线圈的中心距离为196 mm;

5)4个Helmholtz线圈的输入和输出端分别并联在一起，构成一个多层Helmholtz组合线圈;

6)考虑到线圈的匝数多、用铜量大，设计了专门的绝缘骨架来支撑和绕制漆包线.

正方形Helmholtz线圈设计制作完成后，选取线圈内部12个关键测试点进行了磁感应强度测量.测试点的示意图如图8所示，各点的坐标如表1所示［14-15］.

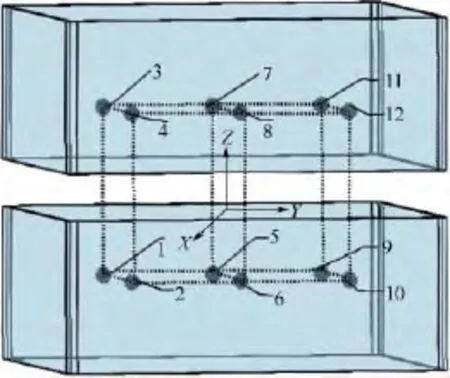
图8 电磁场测试点示意图Fig.8 Schematic diagram of electromagnetic field test point

表1 12个测试点的坐标值Table1 Coordinate values of 12 test points mm

采用HT201数字式特斯拉计/高斯计对上述各点的电磁场进行了测试，分辨力为0.01 mT，误差为±2%.

当正方形Helmholtz线圈中通4 A电流(单根漆包线通过的电流为1A，则可计算出导线中的电流密度Js=1.27 A/mm2).此时，各测试点的磁感应强度如表2所示.

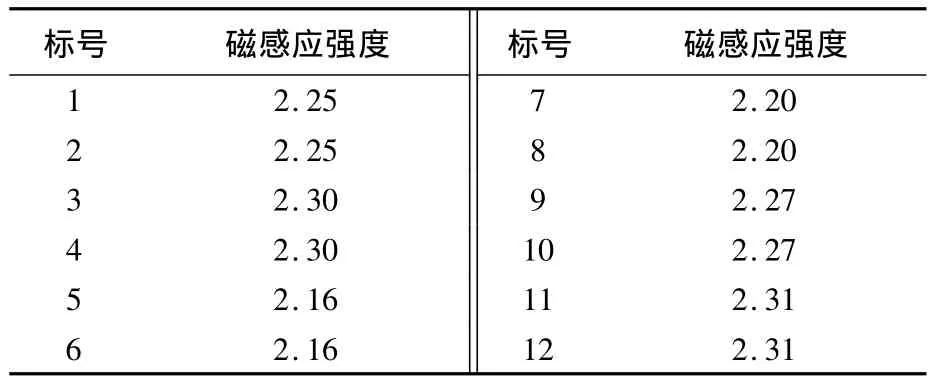
表2 12个测试点的磁感应强度Table2 Magnetic induction of 12 test points mT

从上述12个测试点的测量结果可以看出，线圈内部的磁感应强度与仿真结果基本一致，并且电磁场分布比较均匀，12个测试关键点的磁感应强度的最大差值为0.15 mT，小于0.2 mT，可以满足外层空间物理环境模拟系统测试的需要.

5 结论

1)根据外层空间物理环境模拟系统电磁场模拟的要求，基于Helmholtz线圈的工作原理，采用一对匝数、边长、高度和厚度相同的共轴平行放置的矩形线圈构成正方形Helmholtz线圈，结合恒流源和单片机控制技术，设计了一套电磁场模拟系统.

2)建立了正方形Helmholtz线圈的几何模型和有限元分析模型，采用ANSYS Workbench有限元分析软件对该线圈的电磁场进行了数值模拟，结果表明线圈内部的磁感应强度和电磁场分布的均匀性可以满足测试指标的要求.

3)根据计算结果，设计了正方形Helmholtz线圈的结构参数，实际测试的结果表明，12个关键测试点的电磁场分布均匀，磁感应强度的幅值能够达到2 mT，且最大差值小于0.2 mT，可以满足外层空间物理环境模拟系统测试的需要.

References)

［1］ 齐燕文.空间磁环境模拟技术［J］.航天器环境工程，2005，22(1):19-23.Qi Y W.Space magnetic environment simulation technology［J］.Spacecraft Environment Engineering，2005，22(1):19-23(in Chinese).

［2］ Alamgir A K M，Fang J，Gu C，et al.Square Helmholtz coil with homogeneous field for magnetic measurement of longer HTS tapes［J］.Physica C:Superconductivity，2005，424(1-2):17-24.

［3］ Wang J，She S，Zhang S.An improved Helmholtz coil and analysis of its magnetic field homogeneity［J］.The Review of Scientific Instruments，2002，73(5):2175-2179.

［4］ 司文建，周楠，曹玉松.基于 MATLAB的亥姆霍兹线圈轴线磁场均匀分布的动态仿真［J］.许昌学院学报，2010，29(5):72-74.Si W J，Zhou N，Cao Y S.Dynamic simulation of uniform distribution of the Helmholtz coil magnetic field based on MATLAB［J］.Journal of Xuchang University，2010，29(5):72-74(in Chinese).

［5］ 江俊勤.亥姆霍兹线圈磁场均匀性的研究［J］.广东教育学院学报，2006，26(5):61-66.Jiang J Q.A study on the uniformity of the magnetic field of the Helmholtz coil［J］.Journal of Guangdong Education Institute，2006，26(5):61-66(in Chinese).

［6］ 郑敏.Helmholtz线圈的磁场分布及应用［J］.青海大学学报，2005，23(5):63-64.Zheng M.Analysis and applying of magnetic field in Helmholtz coil［J］.Journal of Qinghai University，2005，23(5):63-64(in Chinese).

［7］ Missakian M.Equations for the magnetic field produced by one or more rectangular loops of wire in the same plane［J］.Journal of Research of the National Institute of Standards and Technology，2000，105(4):557-564.

［8］ 刘翠红，王建永.长方形Helmholtz线圈研究［J］.现代科学仪器，2008(2):29-31.Liu C H，Wang J Y.Study on rectangular Helmholtz coin［J］.Modern Scientific Instruments，2008(2):29-31(in Chinese).

［9］ 郑珂，李光蕊.正方形亥姆霍兹线圈的磁场［J］.安康学院学报，2007，19(3):79-81.Zheng K，Li G R.The magnetic field of square Helmholtz coils［J］.Journal of Ankang University，2007，19(3):79-81(in Chinese).

［10］ 谭曦，刘军，殷建玲.正方形亥姆霍兹线圈的磁场均匀性［J］.光学仪器，2012，34(1):39-44.Tan X，Liu J，Yin J L.The magnetic field uniformity of square Helmholtz coils［J］.Optical Instruments，2012，34(1):39-44(in Chinese).

［11］ 刘坤，张松勇，顾伟.方形亥姆霍兹线圈磁场系统均匀性分析［J］.现代电子技术，2012，35(7):190-194.Liu K，Zhang S Y，Gu W.Analysis on magnetic field homogeneity of magnetic system based on square Helmholtz coils［J］.Modern Electronics Technique，2012，35(7):190-194(in Chinese).

［12］ Lee S G，Kang C S，Chang J W.Square loop coil system for balancing and calibration of second-order SQUID gradiometers［J］.IEEE Transactions on Applied Superconductivity，2007，17(2):3769-3772.

［13］ 刘继亮，李德胜，林恩怀，等.方形亥姆霍兹线圈结构优化设计［J］.仪器仪表学报，2010，31(8):125-128.Liu J L，Li D S，Lin E H，et al.Quadrate Helmholtz coils structure optimization design［J］.Chinese Journal of Scientific Instrument，2010，31(8):125-128(in Chinese).

［14］ 陈修芳.亥姆霍兹线圈磁场分布及其测量［J］.大学物理实验，2009，22(3):125-128.Chen X F.Magnetic field in Helmholtz coil and measurement［J］.Physical Experiment of College，2009，22(3):125-128(in Chinese).

［15］ 李君良，吕玉祥，魏循，等.亥姆霍兹线圈的磁场及其测量［J］.太原理工大学学报，2005，36(5):564-566.Li J L，Lü Y X，Wei X，et al.Magnetic field in Helmholtz loop and measurement［J］.Journal of Taiyuan University of Technology，2005，36(5):564-566(in Chinese).