受通信延迟影响的多UUV队形控制

徐 澎，冯正平

(上海交通大学 船舶海洋与建筑工程学院，上海200240)

0 引 言

多UUV (Unmanned Underwater Vehicle)系统是由多个同构或异构的UUV 组成的具有相互协作能力的系统。与单个UUV 相比，多UUV 系统具备有搭载多样性探测设备、空间分布广和指令与采集数据的双向传输高效等优点。随着水下通信、导航、以及控制等技术的发展，多UUV 系统在水下观测或干预性作业中将发挥越来越重要的作用［1］。

队形控制是多UUV 协调控制领域的一个长久以来的热点［2-5］。群体的协调控制往往需要根据任务的性质要求，设计相应每个个体的控制算法，使得个体按照一定的规则运动或行为，最终使某个物理量趋于一致，比如趋于一致的速度和跟踪同一个目标等。这种通过局部控制，个体间信息交流，使整体实现共同目标的问题称为“一致性”问题。UUV的队形控制和跟踪等都可以看作是一致性问题建模与应用的范畴［6］。有关多UUV 的一致性，最核心的目标是设计一个合理有效的算法或协议，使得网络中每个UUV 都能随着时间的变化而逐渐达到同一状态，或取得一致性［4，7-10］。

由于电磁波在水中衰减远比声波严重，多UUV系统只能依靠水声通信进行协作以实现队形控制。而声波的传播速度尤其在水中要大大低于电磁波，这样水声信号的通信延迟给多UUV 队形控制带来了较大挑战。杨波等引入通信延时，证明了在通信拓扑连通的情况下，只要UUV 之间的通信时延小于某个确定的上界，分布式控制算法将使各UUV 的速度和相对位置渐近地收敛至期望的速度和队形［11-12］。

本文采用具有位置反馈的分布式队形控制体系结构，基于奈奎斯特稳定判据和代数图论给出了队形控制器参数及其容许的统一时延上限，并具有良好的位置和队形镇定效果。

1 受通信约束的队形控制算法

为简化起见，仅考虑固定拓扑和统一通信时延的情况。

假设UUV 动力学简化为质点，实际应用时可以通过对其六自由度方程进行反馈线性化而得。在m维欧几里得空间中考虑n 个质点构成的系统，质点i的动力学方程［2］:

式中:xi∈Rm为质点i 的位置;vi∈Rm为质点i 的速度;ui∈Rm为质点i 的控制输入。

考虑通信时延，这里系统质点之间存在统一的时间延迟。多质点系统队形控制期望多个质点按指定的速度并组成稳定的队形运动，分别规定期望队形几何中心的位置和速度为x*∈Rm和vi∈Rm，且对于每个质点来说都已知。基于一致性协议［8］，设计一个包含通信时延的分布式队形控制算法:

式中:α ＞0 和γ ＞0 为增益系数;ci∈Rm为质点i 的期望位置。

队形控制器(2)同时引入了通信时延τ 和位置反馈，位置反馈对系统的输出有进一步镇定作用，不仅可以加快质点跟踪期望路径的速度，也使得跟踪更加准确。ci表示组成的质点队形固定。当t→∞，xi→ci→x*，vi→v*，即质点以期望的轨迹和速度运动。aij用来指示质点i 和j 之间的通信链路状态:aij=1 则表示二者间链接通路有数据交换，aij=0 则表示没有通信。Ni为质点i 的邻居集，即对所有质点i 可感知的邻居质点j 满足j ∈Ni。τ 反映通信时延对系统控制的影响。

2 与时延有关的队形稳定性

由无向通信拓扑对应的图拉普拉斯矩阵整理n个子系统，系统的误差动力学方程可以表述为

根据代数图拉普拉斯矩阵L 的对称性，其可以转换为一个对角矩阵。令T 为变换矩阵，那么H =TTLT 为对角矩阵并且U = diag(μ1，μ2，…，μn)。依据L 的非负定性，L 的特征值可以表示为一个升序排列0 = μ1≤μ2≤…≤μn－1≤μn。

经过以上转换，闭环系统(3)～(4)的动力学方程被解耦为n 个相互独立的子系统，也即

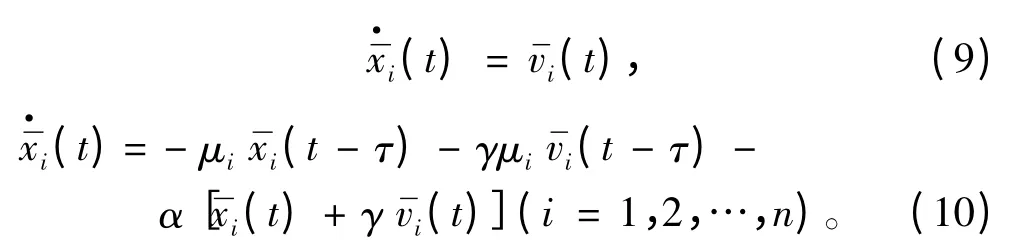
其中

且Im是m × m 单位矩阵。

方程(11)的特征方程为

也即

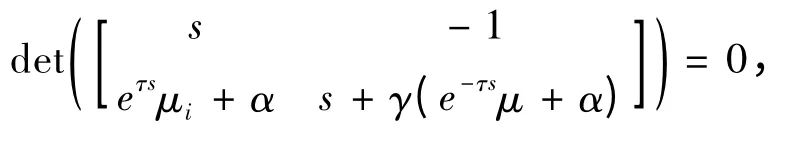
可以得到

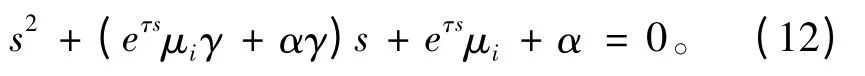
这就是子系统i 的闭环特征方程。

简化为

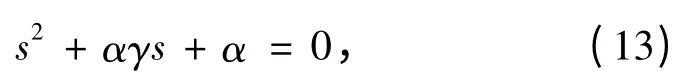
只要α ＞0 和γ ＞0，其稳定性自然满足。

对于其余子系统(i =2，…，n)，方程(12)等效为

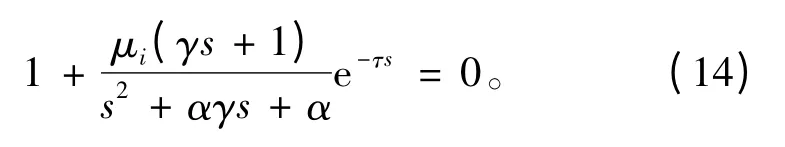
显然第i 个队形控制子系统等效为单位反馈系统，其开环传递函数等效为线性系统Gi(s) =与通信延迟环节串联，其稳定性可由奈奎斯特判据来分析。

由幅值穿越条件

或

其中ωc为幅值穿越频率。

其中为表示方便，用ηi表示第i 个队形控制子系统的穿越频率，即ηi= ωc。需要指出的是α 必须满足0 ＜α ≤μi，i ＞1。

那么稳定性条件可以被转化为求穿越频率ηi下的相位裕度条件，也即

那么由以下不等式可以确定系统能够承受的延迟条件

其中

是自然满足的。

最小的满足延迟条件的τ ＞0 为

那么可由上述结论归纳得出如下定理:考虑n个具有同一的双积分动力学(1)与一个统一的通信延迟的质点。假定通信拓扑无向连通，且每个质点从它的相邻质点接收信息需要经过一个恒定的延迟τ。当τ ＜τ*和α ≤min{μi}，i ＞1，队形控制律(2)可以保证队形稳定，其中

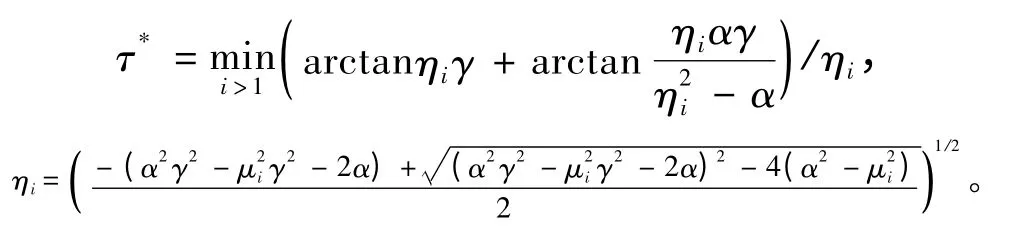
式中μi为代数图拉普拉斯矩阵L 按升序排列的第i个特征值。

3 仿真验证

3.1 多UUV 仿真

采用参考文献［13］的UUV 模型进行仿真研究且仅考虑多UUV 在水平面的队形控制。为此对模型做了合理简化，聚焦于水平面三自由度运动的研究。

UUV 水平面运动方程可写为［14］

式中:M 为惯性矩阵，对称正定，它表示运载器的质量与水动力的附加质量;χ =［xR，yR，ψR］T为UUV在定系中的位置坐标及首向角;ν = ［uR，vR，rR］T为在动系中UUV 的速度向量;C(ν)ν 表示由于UUV 的附加质量，由向心力和哥氏力引起，是反对称的;D(ν)ν 为运载器受到的阻尼等耗散力，因而D(ν)ν是正定的;g(χ)为浮力和重力引起的回复力或力矩;uc= ［uc1，uc2，uc3，uc4］为UUV 水平面上4 个推进器的推力;B 为3 ×4 的输入矩阵，其中的参数表示推力装置的位置;Buc为推力对运载器造成的力或力矩;J(χ)为坐标系变换矩阵，具体见式(23)。

通过对式(21)两边求导得到

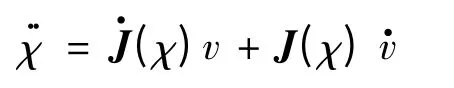
同时易得

式(21)可转化为

所以

转化得到

根据以上推导，采用反馈线性化控制器

定义控制作用f = ［fx，fy，nr］T，则fx，fy为水平面x 和y 方向上直线运动的控制力，nr为偏航控制力矩。根据队形控制器(2)可以实现fx，fy的输出，即u =［fx，fy］T。需要注意，控制力矩nr不会改变UUV的队形和位置。UUV 在运动方向上会受到流体偏航力矩的作用，因而导致UUV 的首向受扰动。为保持UUV 首向在运动过程中恒定，规定控制力矩nr= －2λrR－ λ2ψR，其中λ 为正常数。那么UUV 首向闭环动力学方程整理为显然ψR→0。

以4 个UUV 的队形控制为例。它们的初始队形为一个小正方形。设计一个参考点用于规划运动轨迹，令UUV 进行一个带直角变向的时变运动，其期望速度为v(t)= ［sin(φ(t))，cos(φ(t))］。相应地期望位移用于规定参考点速度的参数如下［10］

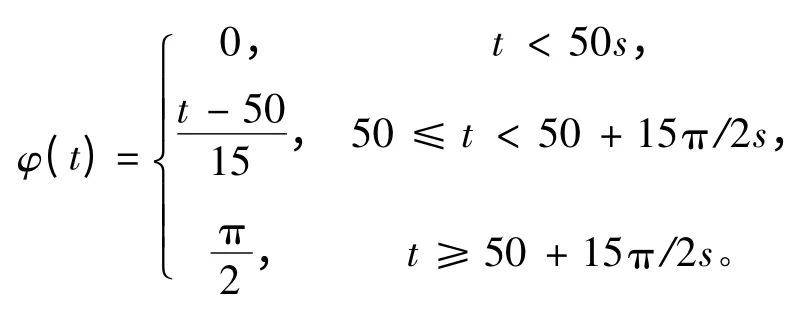
相对位置被规定为

定义ef= (L ⊗Im)(x － c)为队形误差，其中1 = ［1 1 1 1］T。

图1 通信拓扑Fig.1 Communication topology

带统一通信延迟的固定通信拓扑如图1 所示，对应的代数图拉普拉斯矩阵为

其特征值分别为0，2，2 和4。

选取α = 1 和γ = 1 ，根据定理求得可承受延迟为τ*=0.375 0 s。令时间延迟分别为τ=0，0.5τ*和τ*，仿真得到如图2 ～图4 所示的结果。可以看出，期望队形迅速实现并保持v*的移动速度，此外队形误差在5 s 左右开始收敛，达到了队形控制目的。数值仿真的结果与定理的叙述一致。

3.2 与文献［12］的比较

图2 零延迟条件下仿真结果Fig.2 Simulation results under zero delay

图3 延迟τ=0.5τ* 时仿真结果Fig.3 Simulation results under delay of τ=0.5τ*

图4 延迟τ=τ* 时仿真结果Fig.4 Simulation results under delay of τ=τ*

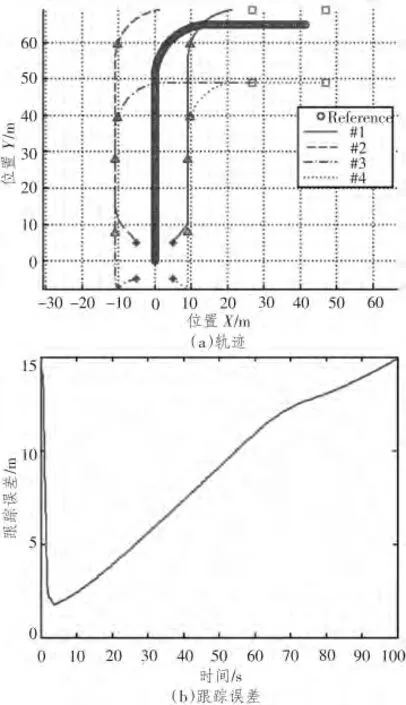
图5 用文献［12］队形控制算法仿真结果Fig.5 Simulation results with algorithms proposed by reference［12］

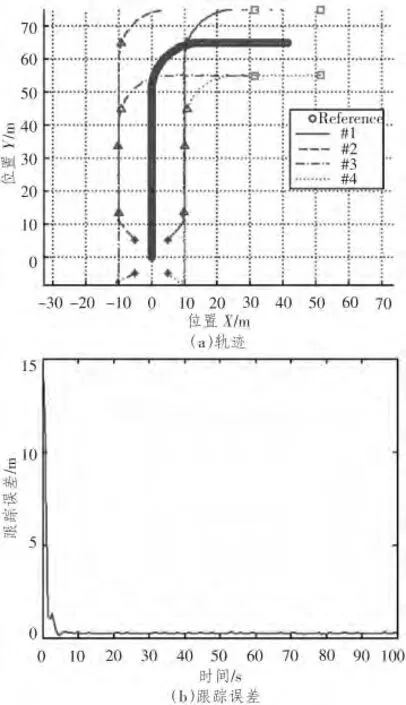
图6 用本文队形控制算法仿真结果Fig.6 Simulation results with algorithms proposed by this paper

做一个简单的仿真，与文献［12］所提算法在性能上进行比较，不失一般性的前提，简化被控对象为质点，并且令4 个质点采用第3.1 节中的通信拓扑，跟踪参考点进行一段含一个直角转弯的轨迹运动。延时条件保持相同，即τ=0.4 s (均符合文献［12］和本文所提定理，即在时延上限以内)，得到仿真结果如图5 和图6 所示。文献［12］与本文所提方法相比虽然在队形误差上差别不大，但从前者的跟踪误差图中可见其跟踪误差发散，再观察其轨迹图，特别在经过直角转弯后，队形中心位置明显偏离了参考点的轨迹。相反，从图6 看出，使用本文所提队形控制算法，跟踪误差可以被有效控制，具体地说，从第5 s开始跟踪误差便收敛到0.2 上下，显示了优越的轨迹跟踪性能。而从图6(a)中也可以观察，队形中心轨迹基本与参考点轨迹重合。这主要是因为本文的算法中引入了位置反馈，在要求被控对象达到期望速度的同时，使其跟踪至相应的参考位置，这对于探测海底指定区域等任务有着实际的意义。

4 结 语

本文利用矩阵图论和奈奎斯特准则，提出了考虑通信时延影响的分布式队形控制算法。该算法针对所有无向通信拓扑的系统，只要通信时延小于某个确定上界，那么所有UUV 的速度、位置和队形将会渐近地收敛到期望值，而且，对比已有的队形控制算法在精确跟踪期望位置有着明显优势。

［1］吴小平.多AUV 协调控制技术研究［D］. 上海:上海交通大学，2008.

［2］FAX J A，MURRAY R M.Information flow and cooperative control of vehicle formations［J］.Automatic Control，IEEE Transactions on，2004，49(9):1465 -1476.

［3］FENG Z，ALLEN R. Formation stabilization of underwater mobile sensing networks［C］.IEEE，2009.

［4］PORFIRI M，ROBERSON D G，STILWELL D J. Tracking and formation control of multiple autonomous agents:a twolevel consensus approach［J］. Automatica，2007，43(8):1318 -1328.

［5］BIAN X，MOU C，YAN Z，et al. Formation coordinated control for multi - AUV based on spatial curve path tracking［C］.IEEE，2011.

［6］BLIMAN P A，FERRARI-TRECATE G.Average consensus problems in networks of agents with delayed communications［J］.Automatica，2008，44(8):1985 -1995.

［7］OLFATI-SABER R.Consensus and cooperation in networked multi-agent systems［J］. Proceedings of the IEEE，2007，95(1).

［8］REN W，BEARD R W，ATKINS E M.Information consensus in multivehicle cooperative control［J］. Control Systems，IEEE，2007，27(2):71-82.

［9］SHENG L，PAN Y J，GONG X.Consensus formation control for a class of networked multiple mobile robot systems［J］.Journal of Control Science and Engineering，2012.

［10］REN W. Consensus strategies for cooperative control of vehicle formations［J］. Control Theory ＆ Applications，IET，2007，1(2):505 -512.

［11］YANG B，FANG H.Forced consensus in networks of double integrator systems with delayed input［J］. Automatica，2010，46(3):629 -632.

［12］杨波，方华京.具有通信约束的分布式水下航行器群编队控制［J］. 华中科技大学学报:自然科学版，2009，37(2):57 -60.YANG Bo，FANG Hua-jing.Finite-time consensus of multiagent systems with communication constraints［J］. Journal of Huazhong University of Science and Technology(Natural Science Edition)，2009，37(2):57 -60.

［13］BRAGA J M A. Control of underwater vehicles on autonomous docking maneuvers［D］.Faculdade de Engenharia da Universidade do Porto，2010.

［14］WADOO S，KACHROO P.Autonomous underwater vehicles:modeling，control design and simulation［M］.Califonia，2010:112-134.