电子商务背景下应急物资分配优化模型研究
2015-12-19周小宁ZHOUXiaoningHAOHaiYANGYong
周小宁, 郝 海, 杨 勇 ZHOU Xiao-ning, HAO Hai, YANG Yong
(天津职业技术师范大学 经济管理学院, 天津300222)
(School of Economics and Management, Tianjin University of Technology and Education, Tianjin 300222, China)
0 引 言
近几年随着电子商务迅速发展, 电子商务交易规模呈现阶梯状上升。 如下图1 所示:
在巨大的交易额背后, 作为“ 第三利润源” 物流必然会成为电子商务的重要组成部分。 低成本、 高效率的物流扩大电子商务范围, 增加效率和效益, 实现电子商务的集成化[1]。 一旦电子商务物流受多方面的影响出现突发事件必然引起重大损失, 特别是电子商务平台采取一些经营销售手段, 消费者需求量呈指数型增长, 物流服务企业做出快速的响应, 是现代物流的要求, 也是电子商务发展的需要。 其快速反应主要是电子商务的物资响应, 目的在于发现突发事件后及时采取有效的应对措施, 防止突发事件的延续性、 破坏性的影响, 尽最大可能将突发损失降到最低, 因此在电子商务背景下研究应急物资分配是有必要的。
对电子商务应急物流加以界定, 电子商务应急物流是指在电子商务背景下, 面对电子商务突发事件(需求扰动、 供应中断、 生产短缺) 的影响, 将实体商品或者服务, 在适当的时间、 地点、 条件, 将适当的实体商品或者服务, 以恰当的成本和方式提供给消费者而进行的计划、 组织、 协调、 指挥和控制的活动。
针对应急物资分配问题, 何建敏[2]提出“ 时间最短” 的概念, 建立带有资源数量约束的单、 多目标和两阶段问题的组合优化模型及求解算法。 李连宏等[3]针对应急系统中多种物资消耗不确定的情况下, 以应急出救点数最少为最优目标, 应急开始时间最早为次优目标, 建立优化模型。 陈达强[4]在考虑“ 应急时间最早”、 “ 参与出救点最少” 多种可能的方案, 针对方案进行成本修正的基础上, 建立应急物流物资响应决策模型。
综上研究所述, 大多数学者都是研究自然灾害突发事件环境下, 对应急物资分配的研究。 本文在电子商务平台商品需求扰动特别是“ 双十一” 时期的需求量暴增的背景下, 建立应急响应模型, 得出最优策略并进行案例仿真分析加以证实, 具有一定的创新并符合现代经济的发展趋势。
1 系统分析和基本假设
将电子商务平台的运营过程看做一个简化的系统,其运作如图2 所示:
在操作过程中网络销售商采取特殊的营销手段(让利、 打折) 等吸引网络消费者需求量大量增加, 拟用脉冲函数如图3 所示的在“ 双十一” 需求量迅速增长, 其物流配送亟需解决。
网络销售商通过电子商务平台现代化的信息处理以及云计算技术处理订单, 将信息反馈给物流服务企业, 物流服务企业在规定的时间、 地点、 条件下将商品运送到顾客的手中。
1.1 系统描述
设“ 双十一” 期间消费者C的需求量商品需求量为y,B1,B2,B3,…,Bn为n个物流服务企业,Bi的配送能力为xi送到C所需时间为不妨设d1≤d2≤d3…≤dn, 如图4 所示:
1.2 系统目标分析
(1) 最短应急响应时间
应急响应时间是对突发事件时间上的紧迫性反应。 当电子商务需求大幅度增加时, 网络销售商和网络消费者均期望物流服务企业能够及时准确地运送到需求者, 达到需求者的期望满意度, 避免退货的发生, 将损失降低到最小。 因此应急时间最短成为应急响应问题的主要目标, 在决策中分析解决。
(2) 物流服务企业数量最少
在电子商务背景下, 网络零售商选择物流服务企业时, 综合考虑的前提下形成契约。 若寻找更多的物流服务企业会额外增加更高的违约费用、 与新企业同盟的诚信损失、 其他潜在的费用。 于是物流服务企业的数量最少应当作为系统分析目标之一。
(3) 成本最低
物流服务企业成本主要包括固定成本和非固定成本。 其中固定成本主要包括固定资产投资、 工人工资等, 非固定成本主要包括运输车辆的油耗、 运输车辆的磨损, 其二者均与运输的距离正相关关系。 为了简化问题, 应急物流总响应成本:
其中Mi为单位距离的配送费用,di为物流服务企业Bi到消费者的配送距离,SCi为物流服务企业的响应固定成本,L为总固定成本, 不随着物流服务企业数量的增加而增加。
一般物流配送的价格相差无几, 若成本最小意味着利润最高, 企业的收益最大, 符合经济学原理。
1.3 基本假设
(1) 物流服务企业在法律、 规定的范围内追求利益最大化。
(2) 网络零售商均是与第三方物流形成契约进行配送。
(3) 消费者无退货现象。
(4) 网络零售商与物流服务企业契约损失无穷大, 尽可能少寻找合作物流企业。
(5) 物流服务企业配送能力能满足顾客的需求。
2 模型的建立
定义1 系统中存在非劣解, 即物流服务企业满足客户的需求, 则存在
定义2 临界下标, 对于从小到大排列的序列xi1≤xi2≤…≤xim其中m≤n, 若存在k为y的临界下标。
定义3 响应时间定义, 假设在应对电子商务突发事件的方案Sh, 其中物流服务企业为p个,dh1,dh2,…,dhn为各自对应的响应时间, 其大小排列为dh1≤dh2…≤dhp, 其中p≤n。
xh1,xh2,…,xhp为相应的物流服务企业的配送量。 方案中Sh的开始时间为最后一家服务企业将最后商品运送给消费者C的时间, 并记为T(Sh), 则方案Sh的响应时间为[4]:
记作所有的非劣解集为V, 响应时间的目标为[4]:
用N(Sh)表示方案Sh的物流服务企业的数量, 则单目标的物流服务企业数量最小的数学关系表示为[4]:
3 算法设计
不难看出, 响应时间T(Sh)最短与物流服务企业的数量N(Sh)最少存在矛盾。 但是, 对于可行方案S*,T(S*)=t*中任意一个“ 时间上” 不比方案S*差的方案S**应满足T(S**)≤T(S*), 则一定存在:
此问题可以转化为让T(S)从大到小取所有的能取到的值, 对N(S)依次迭代寻找最优解。 首先找出最大的即j让x1,x2,…,xj按照大到小的序列排列xi1,xi2,…,xij, 求出该序列对于消费者C的需求量y的临界下标, 并求出非劣方案的解,此时取j=j-1, 依次迭代, 最终达到y无临界下标终止。
若(5) “ =” 同时存在, 用成本进行修正。 根据何健敏[2]算的算法, 本问题算法如下:
(1)i=0,j=n,t=dj。
(2) 对x1,x2,…,xj从大到小排列得xi1,xi2,…,xij并求出序列xi1,xi2,…,xij满足消费需求y的临界下标u。 若存在u,i=i+1, 给出组合方案SK求解T (SK)=j和N(SK)=u, 若不存在u, 转(5) 。
(3)j=j-1。
(4) 若tj=t, 转(3) ; 否则转(2) 。
(5)i=0 时, 无解; 否则用突发事件应急响应成本对结果加以修正。
4 算例与分析
模拟仿真假设某电子商务平台, 消费者需求量为50 单位, 物流服务企业每单位距离收费为2 单位, 且各企业的应急响应成本SCi均为50 单位, 且总固定成本L=8 000, 其信息如表1 所示:

表1 各物流服务企业应急响应数据
应急响应计算过程如表2 所示。
从模拟结果可以看出, 若不考虑成本, 最优方案有两个, 响应时间为8 单位, 即(B7B6B2B8B3或者B7B6B2B3B5。若考虑成本, 最优方案为B7B6B2B3B5, 响应时间为8 个单位。
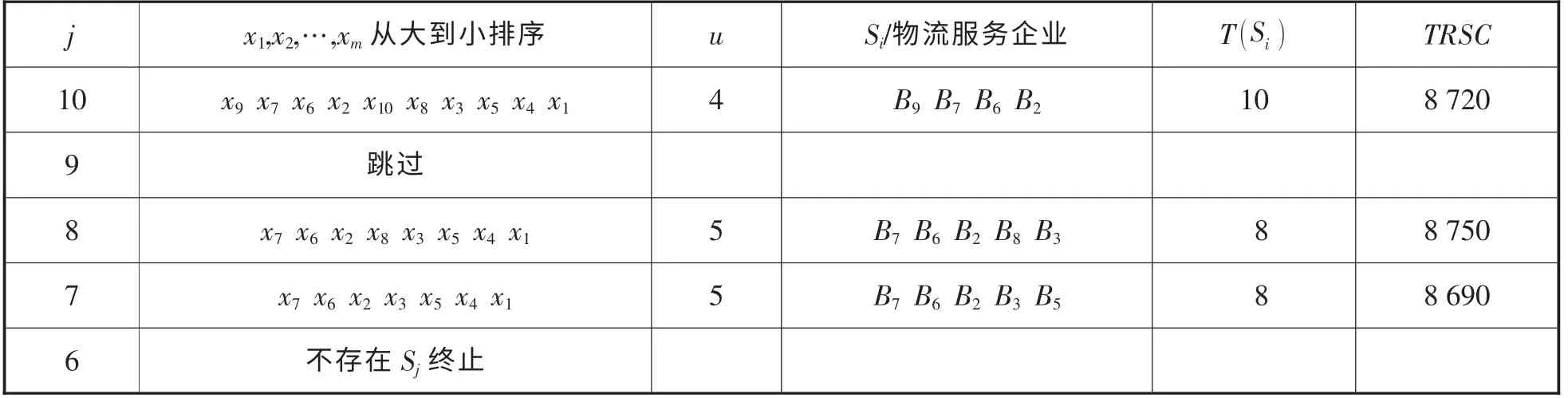
表2 应急响应计算过程
但是在实际中, 根据各个电子商务平台的条件不同以及消费者对需求产品的要求不同, 本文按照Dijkstra 的思想, 对于“ 应急响应时间最短”、 “ 物流服务企业数量”、 “ 成本最低” 多准则决策理论, 对三个目标进行无量纲处理, 再加权的方法,把多目标的问题转化成为单目标问题。
设Qi为无量纲指标:
λi是决策权重可以看做是偏好, 随着不同的企业不同而不同。 其中: 0≤λ1、 λ2、 …λn≤1 且λ1+λ2+…+λn=1。
本算法根据时效性、 诚信性、 经济性三个目标进行无量纲处理:
时效性的无量纲处理:
诚信性的无量纲处理:
经济性的无量纲处理:
其中:TMAX、TMIN分别为期望最大、 最小响应时间,NMAX、NMIN分别为期望最大、 最小物流服务企业数量,TSRCMAX、TSRCMIN为最大、 最小应急响应成本。
综上式(6) 、 (7) 、 (8) 、 (9) 最终决策效用函数为:
最终取Qi最大值为最终决策方案。
假设算例中期望的最大、 最小的应急响应时间为11、 7 单位, 物流服务企业的数量为7、 3 单位, 总的应急响应成本为9 000、 8 500, 假设偏好分别为0.1、 0.1、 0.8, 最终的效用函数
5 结 论
研究电子商务背景下突发事件应急物流决策, 结合“ 应急响应时间最短”、 “ 物流服务企业数量”、 “ 成本最低” 三者的偏好, 将多目标的问题转换为单一目标问题, 并根据案例选出最优方案, 符合应急响应的情景, 为电子商务环境下突发事案件物流决策提供理论基础和解决方案。 但是将消费者的需求看做整体C, 未考虑公路运输的限制能力, 有待进一步研究。
[1] 张昭俊, 卢金钟. 电子商务物流管理[M]. 北京: 清华大学出版社, 2013.
[2] 何建敏, 刘春林, 尤海燕. 应急系统多出救点的选择问题[J]. 系统工程理论与实践, 2001(11):90-93.
[3] 李连宏, 王永军, 李俊峰,等. 多资源非恒定消耗应急调度优化模型研究[J]. 北京理工大学学报, 2006,26(z1):157-160.
[4] 陈达强, 刘南, 缪亚萍. 基于成本修正的应急物流物资响应决策模型[J]. 东南大学学报, 2009,11(1):67-70.
