基于导波模态对称曲线的管道近焊区缺陷识别

张 伟，姜银方，严有琪，雷玉兰，刘秋阁，陈志伟，杜 斌

(1.江苏大学机械工程学院，江苏镇江 212013;2.江苏省特种设备安全监督检验研究院镇江分院，江苏镇江 212009)

随着现代工业的发展和油气资源的开发，长距离管道运输得到了广泛的应用。但是，管道运输事故频频发生，在所发生的事故中，绝大部分管道事发位置在靠近管道对接焊缝区域，该区域因受人为焊接影响，其晶粒粗大，力学性能较差，塑性较母材下降较大，易产生焊接裂纹，因此对管道对接焊缝的缺陷检测具有重大意义［1］。

传统的无损检测方法如超声、涡流、X射线等因具有检测效率低、检测范围窄、必须离线进行检测的缺点，已无法适应工业对管道焊缝快速在线检测的要求。长距离超声导波技术［2］是利用超声导波沿管道内壁传播遇到介质突变时发生反射的原理进行缺陷识别，该技术与传统的超声波检测技术相比具有检测范围广，检测效率高和在管道某一处实现全方位检测的特点，引起世界范围内广泛的研究。Lowe M J S［3］等提出用L(0，2)模态导波进行检测，并证明L(0，2)模态导波适用于长距离检测。Li等［4－5］提出了位移圆周分布调制聚焦技术，通过改变传感器阵列中各单元的激励信号幅值系数和时间延迟参数，将导波能量集中在某一个小的区域，最终通过轴向和周向的扫描获得焊缝缺陷的相关信息。程载斌［6］等进行了管道纵向导波裂纹检测数值模拟的识别研究，对管道一端激励纵向导波，同端接收反射应力波，通过对接收信号位置周向各节点位移时程曲线进行叠加，确定裂纹回波和端面回波的位置。为了增强超声导波的检测能力，并实现缺陷的圆周定位，姜秀娟［7］等利用数值模拟的方法对含有裂纹和焊缝两种缺陷形式的管道进行分析，发掘了超声导波技术在焊缝和裂纹同时存在时缺陷检测的能力。虽然国内外利用导波技术对管道检测展开的大量研究，但是鲜有针对近焊区裂纹缺陷的识别技术。

本文利用压电传感器发射和接收纵向导波信号的原理，对长直管道近焊区裂纹缺陷进行研究。研究内容包括:(1)建立管道导波试验系统，提出模态对称理论，根据该理论设计模态对称算法，根据对称算法建立波形模态对称曲线用于辅助近焊缝区缺陷的识别，并研究模态对称曲线与管道近焊区缺陷的关系。(2)通过小波包能量谱分析方法，研究不同频带下的能量分布特征，研究导波能量在焊缝缺陷处的聚焦。

1 管道导波模态对称理论

无限长空心管道的导波传播特性相当复杂，建立如图1管道柱状坐标系进行描述，假设空心圆柱是轴对称、且无限长的，材料特性是均匀的、各向同性的线性弹性体，并且其边界条件都为自由面，则空间质点的3 个位移分量［8］为

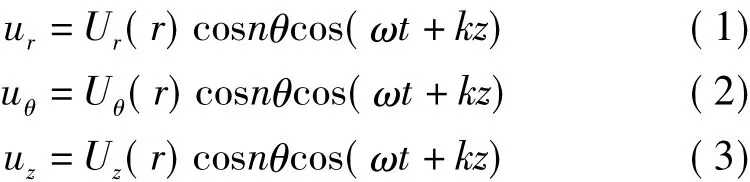
其中，ur，uθ，uz分别为径向、周向和轴向位移分量，为圆周方向的阶次;ω 为角频率;k为波数;Ur，Uθ，Uz分别为径向、周向和轴向位移幅度，这3个解分别对应管道导波的3种模态，包括对称模态(纵向模态、剪切模态)和非对称模态(弯曲模态)。导波在传播中遇到管道结构突变会发生模态转换的现象［9］。由于管道检测的导波为对称模态，若缺陷在管道圆周方向上为非对称，则反射波通常也呈现非对称，即为弯曲模态导波［10］。随着缺陷的圆周对称度增大，转换模态导波的幅值呈线性递减。圆周对称度用百分数表示，如图2所示。

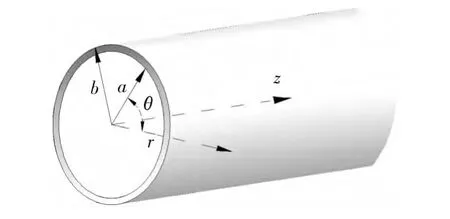
图1 管道圆柱坐标系

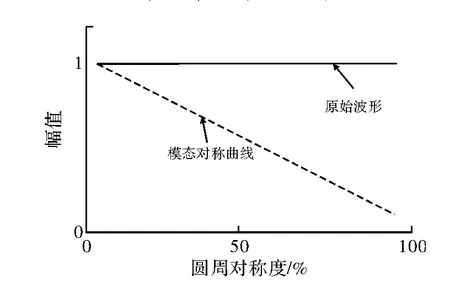
图2 模态对称识别原理图

假设沿管道外壁周向均布N个压电传感器，采取整环激励、单个传感器信号采集的方式，共得到S1～SN组回波信号，依次选择两个圆周对称传感器信号的绝对幅值进行叠加并取均值，得到以下模态对称曲线算法

其中，Y为模态对称曲线的幅值;FS1～FSN为个传感器在管道对应母线上所有信号的幅值。

2 试验装置

试验装置如图3所示，通过在计算机用公式编辑器编写汉宁窗调制的多个单音频信号，使其产生所需的激励波形。此信号经导波诊断仪主机后施加于管道端部PZT－5压电传感器阵列。激励环由均布排列16个相同规格压电传感器组成，采集环由8个均布排列的压电传感器组成，通过激励纵向L(0，2)模态进行导波检测检测频率范围为60～100 kHz，激励频率步进长度为5 kHz。

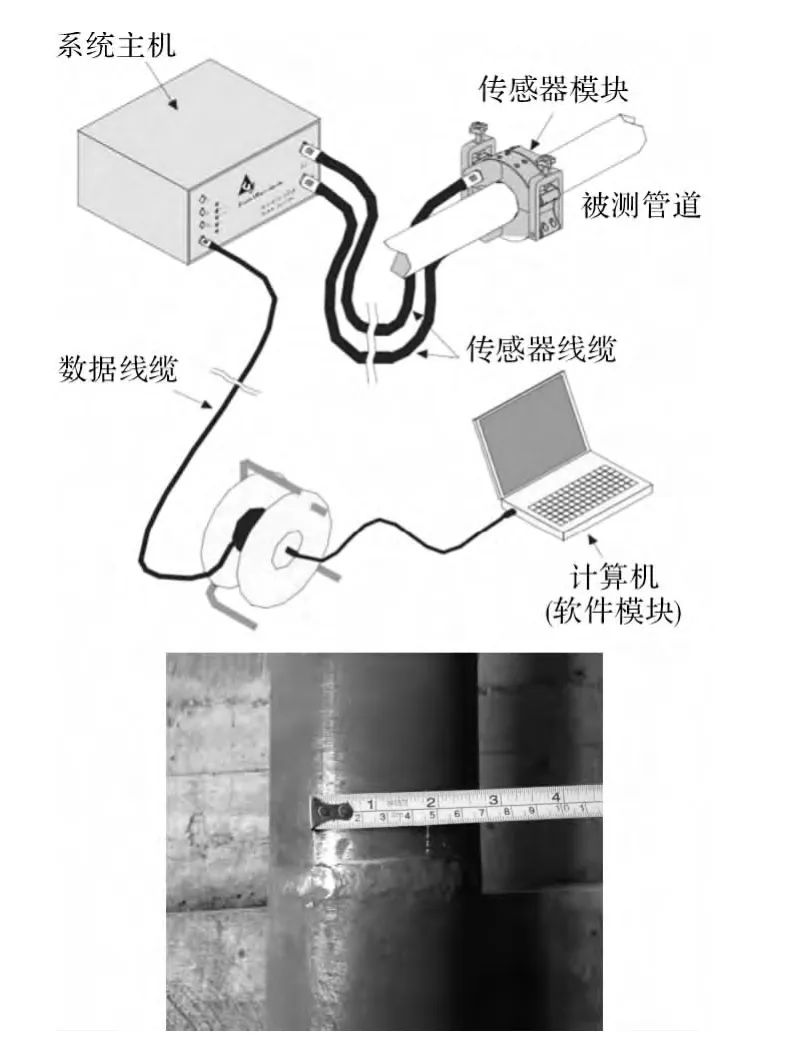
图3 实验装置图

以带环焊缝的管道(管道长度为11.5 m，管道外径108 mm，壁厚6 mm，环焊缝在5.75 m处)为研究对象，通过在焊缝近焊区人工制作裂纹，裂纹截面积比分别为4%，6%和10%，研究管道焊缝热影响区裂纹在不同缺陷截面积比的情况下，整环接收波形经对称叠加算法处理后的对称性曲线，其中裂纹截面积比是指横向截面上裂纹面积占整个截面面积的百分比。

3 试验结果与分析

3.1 试验结果与模态对称曲线的绘制

采集整环传感器信号，计算在裂纹缺陷截面积比分别为4%，6%和10%焊缝回波反射系数，即焊缝回波幅值与激励波幅值之比。试验发现，随着激励频率的改变，焊缝回波的幅值也发生改变，如图4所示，缺陷不断加大时，焊缝回波反射系数并非成线性升高，且焊缝回波信号与裂纹信号混叠，难以辨别近焊区缺陷。

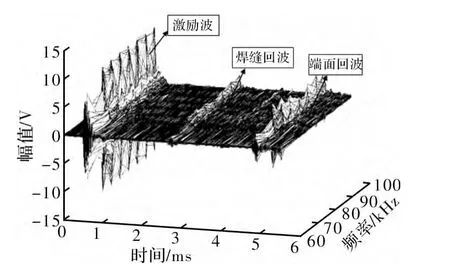
图4 变频率下焊缝回波幅值

通过整环传感器激励单个传感器接收的方式，将单个传感器接收到的信号的起始位置对齐，采用模态对称算法，绘制出对称性曲线，由于采集的波形具有一定的噪声，给缺陷识别带来困难，采用小波滤波方法，滤除其杂波［11－12］。为了便于波形的识别和后续的信号处理，需要取其包络线，求包络时，先求出信号中的极大值和极小值，然后利用这些最大值或最小值作为初始数据，通过3次样条插值和拟合方法拟合出上包络。然后通过 Matlab软件编程，绘制波形的上包络线。如图5与图6所示，可以直观地看出在管道环焊缝近焊区存在缺陷时幅值明显高于在无缺陷工况下的幅值。

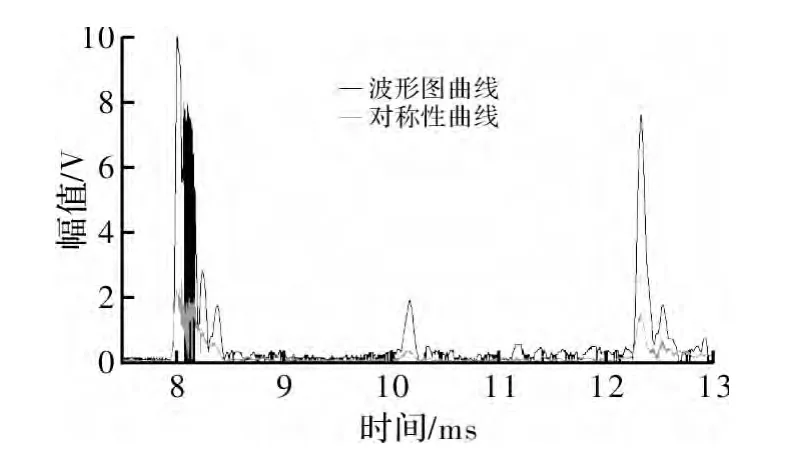
图5 无缺陷波形图与模态对称性曲线

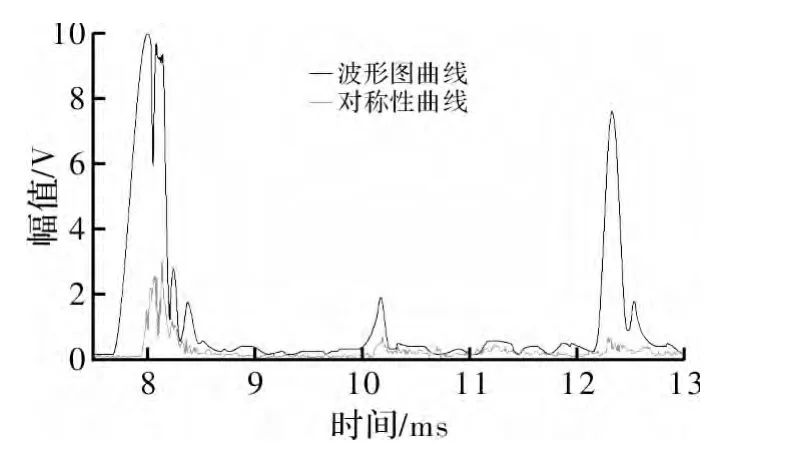
图6 带缺陷波形图与对称性曲线

3.2 小波包能量谱分析

能量系数是表征金属材料在损伤、断裂状态下的最佳参数，由于管道对接焊缝是圆周对称结构，若焊缝存在缺陷必会打破对称分布，管道对接焊缝热影响区组织较密，遇到缺陷在该处的能量会有相应变化，利用小波包分析法在频带上的精细分解，提取不同频带的能量分布，利用对称能量特征对比完好焊缝与带裂纹缺陷焊缝识别管道焊区裂纹，并证实该特征对检测焊缝裂纹缺陷的有效性。对称能量系数指利用小波包分析方法将单路回波信号分解到不同频带内，计算出各路回波信号在不同频带内的归一化能量比。

小波包分析是管道检测信号的一种有效处技术，相比小波分析技术，小波包分析能够在信号低频区和高频区域同时进行向下二进分解，可获得精确的频率分辨率，通过对时域信号进行小波包分解，可描述信号在不同频段下相应成份的信号强度随时间变化的物理特性。理论上而言，随着小波包分解层数的增加，信号频域将被划分的更细，局部特征也将更明显。同时，其频率的分辨率也更高。但实际情况下，由于小波包分解采用的“下取样”不能同时满足频域和时域的高分辨率。所以，在对信号充分分解的同时选取合适的分解层数就显得尤为重要，根据在时域中信号的对称性，选择db4小波，分解层数为3层，分别对单个传感器进行信号采集，计算第3层归一化能量值。

通过在管道一处周向位置预制人工裂纹缺陷，将采集到的信号进行小波包分解，计算此处周向能量值与整环传感器接收信号能量值比，如图7与图8，比较在管道焊缝近焊区有无缺陷导波信号发现，不带缺陷的管道环焊缝区能量集中在90～100 kHz，带有裂纹的管道环焊缝近焊区能量集聚在70～80 kHz频率段，在时间－幅值平面上表现为经对称叠加后幅值的升高。当激励导波频率在70～80 kHz时，通过不断加大缺陷后发现，管道焊缝缺陷处模态对称曲线幅值升高，如图9所示。

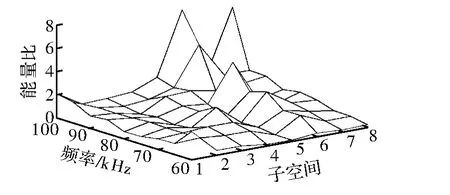
图7 管道无缺陷小波子空间能量比

图8 带裂纹焊缝小波子空间能量比

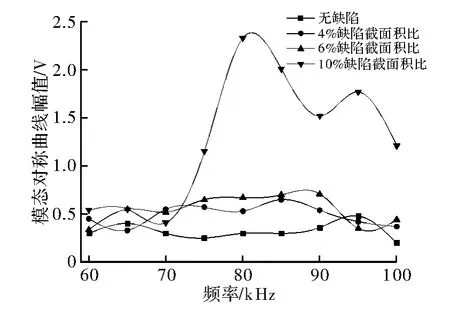
图9 模态对称曲线幅值随缺陷大小变化

4 结束语

研究管道焊区导波信号特征参数对于焊缝中的缺陷识别起着至关重要的作用，本文基于超声导波检测技术，进行管道对接焊缝热影响区缺陷的实验研究，通过在管道环焊缝近焊区人工制作裂纹缺陷，获得所需缺陷信号。并结合近焊区缺陷信号探寻缺陷大小与模态对称曲线的关系。

(1)通过编写出模态对称曲线算法，并根据该算法编制出辅助缺陷识别的模态对称曲线。进行管道导波检测试验，通过人工制作缺陷的方法验证了当近焊区存在缺陷时，对称曲线幅值升高，且随着缺陷截面积比越大，相同位置的对称曲线幅值越高。

(2)通过小波包能量谱分析方法，得出带裂纹管道对接焊缝处的能量与无缺陷时相比，导波在缺陷处聚焦，且聚焦频率为70～80 kHz的区间中。

［1］ 熊庆人，闫琳，张建勋，等．X80钢级管道环焊缝非均匀裂纹体断裂驱动力［J］．焊接学报，32(6):29－33．

［2］ 孙凯，孟光，叶林，等．基于超声导波的钢梁结构损伤大小识别研究［J］．振动与冲击，2011，30(9):227 －231．

［3］ Lowe M J S，Alleyne D N，Cawley P．Detection in pipes using guided waves［J］．Ultrasonics，1998，36(1):147 －154．

［4］ Li Jian，Rose J L．Natural beam focusing of non － axisymmetric guided waves in large － diameter pipes［J］．Ultrasonics，2006，44(3):35 －45．

［5］ LI Jian，Rose J L．Excitation and propagation of non － axisymmetric guided waves in a hollow cylinder［J］．Acoustical Society of American，2001，109(2):457 －464．

［6］ 程载斌，王志华，张立军，等．管道超声纵向导波裂纹检测数值模拟［J］．应用力学学报，2004，21(4):76 －80．

［7］ 姜秀娟．管道焊区裂纹缺陷的超声导波检测研究［D］．保定:华北电力大学，2010．

［8］ Ditri J J．Utilization of guided elastic waves for the characterization of circumferential cracks in hollow cylinders［J］．A-coustical Society of American，1994，96(6):3769 －3775．

［9］ 邓菲，吴斌，何存富．管道导波检测中的位移圆周分布调制方法［J］．机械工程学报，2009，45(4):39－45．

［10］Rose Joseph．固体中的超声波［M］．何存富，译．北京:科学出版社，2004．

［11］张德丰．小波分析［M］．北京:机械工业出版社，2010．

［12］宋振华，王志华，马宏伟．基于小波分析的超声导波管道裂纹检测方法研究［J］．固体力学学报，2010，30(4):368－375．